En geometría diferencial, el teorema de las tres geodésicas , también conocido como teorema de Lyusternik-Schnirelmann , establece que cada variedad de Riemann con topología de una esfera tiene al menos tres geodésicas cerradas simples (es decir, tres círculos geodésicos incrustados). [1] El resultado también se puede extender a cuasigeodésicas sobre un poliedro convexo y a geodésicas cerradas de 2 esferas reversibles de Finsler . El teorema es claro: aunque cada 2 esferas de Riemann contiene infinitas geodésicas cerradas distintas, se garantiza que sólo tres de ellas no tendrán autointersecciones. Por ejemplo, según un resultado de Morse , si las longitudes de los tres ejes principales de un elipsoide son distintas, pero suficientemente cercanas entre sí, entonces el elipsoide tiene sólo tres geodésicas cerradas simples. [2]
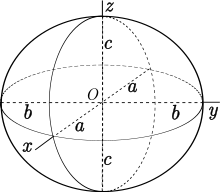
Una geodésica , sobre una superficie riemanniana, es una curva que es localmente recta en cada uno de sus puntos. Por ejemplo, en el plano euclidiano las geodésicas son líneas , y en la superficie de una esfera las geodésicas son círculos máximos . El camino más corto en la superficie entre dos puntos es siempre una geodésica, pero también pueden existir otras geodésicas. Se dice que una geodésica es cerrada si regresa a su punto inicial y dirección inicial; al hacerlo, puede cruzarse varias veces. El teorema de las tres geodésicas dice que para superficies homeomorfas a la esfera, existen al menos tres geodésicas cerradas que no se cruzan solas. Puede haber más de tres; por ejemplo, la esfera misma tiene infinitos.
Este resultado surge de las matemáticas de la navegación oceánica, donde la superficie de la Tierra se puede modelar con precisión mediante un elipsoide , y del estudio de las geodésicas en un elipsoide , los caminos más cortos para que viajen los barcos. En particular, un elipsoide triaxial casi esférico tiene sólo tres geodésicas cerradas simples, sus ecuadores. [3] En 1905, Henri Poincaré conjeturó que toda superficie lisa topológicamente equivalente a una esfera contiene también al menos tres geodésicas cerradas simples, [4] y en 1929 Lazar Lyusternik y Lev Schnirelmann publicaron una prueba de la conjetura; Si bien el argumento topológico general de la prueba era correcto, empleó un resultado de deformación que luego se descubrió que era defectuoso. [5] Varios autores propusieron soluciones insatisfactorias a la brecha. Grayson proporcionó una solución universalmente aceptada en la década de 1980 mediante la curva de acortamiento del flujo [6].
Una versión reforzada del teorema establece que, en cualquier superficie de Riemann que sea topológicamente una esfera, existen necesariamente tres geodésicas cerradas simples cuya longitud es como máximo proporcional al diámetro de la superficie. [7]
El número de geodésicas cerradas de longitud máxima L en una esfera topológica suave crece en proporción a L /log L , pero no se puede garantizar que todas esas geodésicas sean simples. [8]
En superficies de Riemann hiperbólicas compactas , hay infinitas geodésicas cerradas simples, pero solo un número finito con un límite de longitud determinado. Están codificados analíticamente por la función zeta de Selberg . Maryam Mirzakhani investigó la tasa de crecimiento del número de geodésicas cerradas simples, en función de su longitud . [9]
La existencia de tres geodésicas cerradas simples también es válida para cualquier métrica reversible de Finsler en la 2 esfera. [10]
¿Existe un algoritmo que pueda encontrar una cuasigeodésica cerrada simple en un poliedro convexo en tiempo polinómico?
También es posible definir geodésicas en algunas superficies que no son lisas en todas partes, como los poliedros convexos . La superficie de un poliedro convexo tiene una métrica que es localmente euclidiana excepto en los vértices del poliedro, y una curva que evita los vértices es una geodésica si sigue segmentos de línea recta dentro de cada cara del poliedro y se mantiene recta a lo largo de cada borde del poliedro. que cruza. Aunque algunos poliedros tienen geodésicas cerradas simples (por ejemplo, el tetraedro regular y los disfenoides tienen infinitas geodésicas cerradas, todas simples) [11] [12] otros no. En particular, una geodésica cerrada simple de un poliedro convexo necesariamente bisectaría el defecto angular total de los vértices, y casi todos los poliedros no tienen tales bisectrices. [3] [11]
Sin embargo, el teorema de las tres geodésicas se puede extender a poliedros convexos considerando cuasigeodésicas, curvas que son geodésicas excepto en los vértices de los poliedros y que tienen ángulos menores que π en ambos lados en cada vértice que cruzan. Una versión del teorema de las tres geodésicas para poliedros convexos establece que todos los poliedros tienen al menos tres cuasigeodésicas cerradas simples; esto se puede demostrar aproximando el poliedro por una superficie lisa y aplicando el teorema de las tres geodésicas a esta superficie. [13] Es un problema abierto si alguna de estas cuasigeodésicas puede construirse en tiempo polinomial . [14] [15]