Estimación de la densidad espectral

Técnica de procesamiento de señales

En el procesamiento estadístico de señales , el objetivo de la estimación de densidad espectral ( SDE ) o simplemente estimación espectral es estimar la densidad espectral (también conocida como densidad espectral de potencia ) de una señal a partir de una secuencia de muestras de tiempo de la señal. ^[1] Intuitivamente hablando, la densidad espectral caracteriza el contenido de frecuencia de la señal. Un propósito de estimar la densidad espectral es detectar cualquier periodicidad en los datos, observando picos en las frecuencias correspondientes a estas periodicidades.

Algunas técnicas de SDE suponen que una señal está compuesta por un número limitado (normalmente pequeño) de frecuencias generadoras más ruido y tratan de encontrar la ubicación e intensidad de las frecuencias generadas. Otras no hacen ninguna suposición sobre el número de componentes y tratan de estimar todo el espectro generador.

Descripción general

Ejemplo de forma de onda de voz y su espectro de frecuencia

Una forma de onda periódica ( onda triangular ) y su espectro de frecuencia, que muestra una frecuencia "fundamental" de 220 Hz seguida de múltiplos (armónicos) de 220 Hz

La densidad espectral de potencia de un segmento de música se estima mediante dos métodos diferentes, a modo de comparación.

El análisis espectral , también conocido como análisis del dominio de la frecuencia o estimación de la densidad espectral, es el proceso técnico de descomponer una señal compleja en partes más simples. Como se describió anteriormente, muchos procesos físicos se describen mejor como una suma de muchos componentes de frecuencia individuales. Cualquier proceso que cuantifique las diversas cantidades (por ejemplo, amplitudes, potencias, intensidades) en función de la frecuencia (o fase ) se puede llamar análisis espectral .

El análisis del espectro se puede realizar en toda la señal. Alternativamente, una señal se puede dividir en segmentos cortos (a veces llamados cuadros ) y el análisis del espectro se puede aplicar a estos segmentos individuales. Las funciones periódicas (como ) son particularmente adecuadas para esta subdivisión. Las técnicas matemáticas generales para analizar funciones no periódicas caen dentro de la categoría del análisis de Fourier . ${\displaystyle \sin(t)}$

La transformada de Fourier de una función produce un espectro de frecuencia que contiene toda la información sobre la señal original, pero en una forma diferente. Esto significa que la función original puede ser reconstruida completamente ( sintetizada ) mediante una transformada de Fourier inversa . Para una reconstrucción perfecta, el analizador de espectro debe preservar tanto la amplitud como la fase de cada componente de frecuencia. Estas dos piezas de información pueden representarse como un vector bidimensional, como un número complejo o como magnitud (amplitud) y fase en coordenadas polares (es decir, como un fasor ). Una técnica común en el procesamiento de señales es considerar la amplitud al cuadrado, o potencia ; en este caso, el gráfico resultante se conoce como espectro de potencia .

Debido a su reversibilidad, la transformada de Fourier se considera una representación de la función en términos de frecuencia en lugar de tiempo; por lo tanto, es una representación del dominio de la frecuencia . Las operaciones lineales que se pueden realizar en el dominio del tiempo tienen contrapartes que a menudo se pueden realizar con mayor facilidad en el dominio de la frecuencia. El análisis de frecuencia también simplifica la comprensión e interpretación de los efectos de varias operaciones del dominio del tiempo, tanto lineales como no lineales. Por ejemplo, solo las operaciones no lineales o variables en el tiempo pueden crear nuevas frecuencias en el espectro de frecuencias.

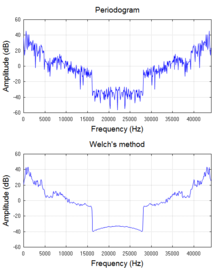
En la práctica, casi todo el software y los dispositivos electrónicos que generan espectros de frecuencia utilizan una transformada de Fourier discreta (DFT), que opera sobre muestras de la señal y que proporciona una aproximación matemática a la solución integral completa. La DFT se implementa casi invariablemente mediante un algoritmo eficiente llamado transformada rápida de Fourier (FFT). La matriz de componentes de magnitud cuadrada de una DFT es un tipo de espectro de potencia llamado periodograma , que se usa ampliamente para examinar las características de frecuencia de funciones libres de ruido, como respuestas al impulso del filtro y funciones de ventana . Pero el periodograma no proporciona ganancia de procesamiento cuando se aplica a señales similares al ruido o incluso a sinusoides en relaciones señal-ruido bajas ^{[ ¿por qué? ]} . En otras palabras, la varianza de su estimación espectral a una frecuencia dada no disminuye a medida que aumenta el número de muestras utilizadas en el cálculo. Esto se puede mitigar promediando en el tiempo ( método de Welch ^[2] ) o en la frecuencia ( suavizado ). El método de Welch se usa ampliamente para la estimación de la densidad espectral (SDE). Sin embargo, las técnicas basadas en periodogramas introducen pequeños sesgos que son inaceptables en algunas aplicaciones, por lo que en la siguiente sección se presentan otras alternativas.

Técnicas

Se han desarrollado muchas otras técnicas de estimación espectral para mitigar las desventajas del periodograma básico. Estas técnicas generalmente se pueden dividir en métodos no paramétricos , paramétricos y , más recientemente, semiparamétricos (también llamados dispersos). ^[3] Los enfoques no paramétricos estiman explícitamente la covarianza o el espectro del proceso sin asumir que el proceso tenga ninguna estructura particular. Algunos de los estimadores más comunes en uso para aplicaciones básicas (por ejemplo, el método de Welch ) son estimadores no paramétricos estrechamente relacionados con el periodograma. Por el contrario, los enfoques paramétricos suponen que el proceso estocástico estacionario subyacente tiene una cierta estructura que se puede describir utilizando un pequeño número de parámetros (por ejemplo, utilizando un modelo autorregresivo o de promedio móvil ). En estos enfoques, la tarea es estimar los parámetros del modelo que describe el proceso estocástico. Cuando se utilizan los métodos semiparamétricos, el proceso subyacente se modela utilizando un marco no paramétrico, con el supuesto adicional de que el número de componentes distintos de cero del modelo es pequeño (es decir, el modelo es disperso). También se pueden utilizar enfoques similares para la recuperación de datos faltantes ^[4], así como para la reconstrucción de señales .

A continuación se muestra una lista parcial de técnicas de estimación de densidad espectral:

• Métodos no paramétricos en los que las muestras de señal pueden estar espaciadas de manera desigual en el tiempo ( los registros pueden estar incompletos )
  • Análisis espectral de mínimos cuadrados , basado en el ajuste de mínimos cuadrados a frecuencias conocidas
  • Periodograma de Lomb-Scargle , una aproximación del análisis espectral de mínimos cuadrados
  • Transformada de Fourier discreta no uniforme

• Métodos no paramétricos en los que las muestras de señal deben estar espaciadas uniformemente en el tiempo ( los registros deben estar completos ):
  • Periodograma , el módulo al cuadrado de la transformada de Fourier discreta
  • El método de Bartlett es el promedio de los periodogramas tomados de múltiples segmentos de la señal para reducir la varianza de la estimación de la densidad espectral.
  • El método de Welch es una versión con ventana del método de Bartlett que utiliza segmentos superpuestos.
  • Multitaper es un método basado en periodogramas que utiliza múltiples estrechamientos, o ventanas, para formar estimaciones independientes de la densidad espectral para reducir la varianza de la estimación de la densidad espectral.
  • El análisis del espectro singular es un método no paramétrico que utiliza una descomposición en valores singulares de la matriz de covarianza para estimar la densidad espectral.
  • Transformada de Fourier de corta duración
  • El filtro crítico es un método no paramétrico basado en la teoría del campo de información que puede abordar el ruido, los datos incompletos y las funciones de respuesta instrumental.
• Técnicas paramétricas (lista incompleta):
  • Estimación del modelo autorregresivo (AR), que supone que la muestra n está correlacionada con las p muestras anteriores.
  • Estimación del modelo de promedio móvil (MA), que supone que la muestra n está correlacionada con términos de ruido en las p muestras anteriores.
  • Estimación de promedio móvil autorregresivo (ARMA), que generaliza los modelos AR y MA.
  • La clasificación de múltiples señales (MUSIC) es un método de superresolución popular .
  • La estimación de parámetros de señal mediante técnicas de invariancia rotacional (ESPRIT) es otro método de superresolución.
  • La estimación espectral de máxima entropía es un método de todos los polos útil para SDE cuando se esperan características espectrales singulares, como picos agudos.
• Técnicas semiparamétricas (lista incompleta):
  • Estimación basada en covarianza iterativa SParse (SPICE) ^[3] y la estimación más generalizada -SPICE ^[5] . ${\displaystyle (r,q)}$
  • Estimación mediante el método iterativo adaptativo (IAA). ^[6]
  • Lasso , similar al análisis espectral de mínimos cuadrados pero con una penalización que impone escasez. ^[7]

Estimación paramétrica

En la estimación espectral paramétrica, se supone que la señal está modelada por un proceso estacionario que tiene una función de densidad espectral (SDF) que es una función de la frecuencia y los parámetros . ^[8] El problema de estimación entonces se convierte en uno de estimación de estos parámetros. ${\displaystyle S(f;a_{1},\ldots ,a_{p})}$ ${\displaystyle f}$ ${\displaystyle p}$ ${\displaystyle a_{1},\ldots ,a_{p}}$

La forma más común de estimación de SDF paramétrica utiliza como modelo un modelo autorregresivo de orden . ^{[8] : 392} Una secuencia de señales que obedece a un proceso de media cero satisface la ecuación ${\displaystyle {\text{AR}}(p)}$ ${\displaystyle p}$ ${\displaystyle \{Y_{t}\}}$ ${\displaystyle {\text{AR}}(p)}$

${\displaystyle Y_{t}=\phi _{1}Y_{t-1}+\phi _{2}Y_{t-2}+\cdots +\phi _{p}Y_{t-p}+\epsilon _{t},}$

donde son coeficientes fijos y es un proceso de ruido blanco con media cero y varianza de innovación . La SDF para este proceso es ${\displaystyle \phi _{1},\ldots ,\phi _{p}}$ ${\displaystyle \epsilon _{t}}$ ${\displaystyle \sigma _{p}^{2}}$

${\displaystyle S(f;\phi _{1},\ldots ,\phi _{p},\sigma _{p}^{2})={\frac {\sigma _{p}^{2}\Delta t}{\left|1-\sum _{k=1}^{p}\phi _{k}e^{-2i\pi fk\Delta t}\right|^{2}}}\qquad |f|<f_{N},}$

con el intervalo de tiempo de muestreo y la frecuencia de Nyquist . ${\displaystyle \Delta t}$ ${\displaystyle f_{N}}$

Existen varios enfoques para estimar los parámetros del proceso y, por tanto, la densidad espectral: ^{[8] : 452-453} ${\displaystyle \phi _{1},\ldots ,\phi _{p},\sigma _{p}^{2}}$ ${\displaystyle {\text{AR}}(p)}$

• Los estimadores de Yule-Walker se obtienen resolviendo recursivamente las ecuaciones de Yule-Walker para un proceso ${\displaystyle {\text{AR}}(p)}$
• Los estimadores de Burg se obtienen al tratar las ecuaciones de Yule-Walker como una forma de problema de mínimos cuadrados ordinarios. Los estimadores de Burg generalmente se consideran superiores a los estimadores de Yule-Walker. ^{[8] : 452} Burg los asoció con la estimación espectral de máxima entropía . ^[9]
• Los estimadores de mínimos cuadrados de avance-retroceso tratan el proceso como un problema de regresión y lo resuelven utilizando el método de avance-retroceso. Son competitivos con los estimadores de Burg. ${\displaystyle {\text{AR}}(p)}$
• Los estimadores de máxima verosimilitud calculan los parámetros utilizando un método de máxima verosimilitud . Esto implica una optimización no lineal y es más complejo que los tres primeros.

Los métodos paramétricos alternativos incluyen el ajuste a un modelo de promedio móvil (MA) y a un modelo de promedio móvil autorregresivo completo (ARMA).

Estimación de frecuencia

La estimación de frecuencia es el proceso de estimar la frecuencia , la amplitud y el desplazamiento de fase de una señal en presencia de ruido dadas suposiciones sobre el número de componentes. ^[10] Esto contrasta con los métodos generales anteriores, que no hacen suposiciones previas sobre los componentes.

Tono único

Si solo se desea estimar la frecuencia de la señal de tono puro más fuerte , se puede utilizar un algoritmo de detección de tono .

Si la frecuencia dominante cambia con el tiempo, entonces el problema pasa a ser la estimación de la frecuencia instantánea tal como se define en la representación tiempo-frecuencia . Los métodos para la estimación de la frecuencia instantánea incluyen aquellos basados ​​en la distribución de Wigner-Ville y funciones de ambigüedad de orden superior . ^[11]

Si uno quiere conocer todos los componentes de frecuencia (posiblemente complejos) de una señal recibida (incluyendo la señal transmitida y el ruido), se utiliza un enfoque de tonos múltiples.

Tonos múltiples

Un modelo típico de una señal consiste en una suma de exponenciales complejos en presencia de ruido blanco , ${\displaystyle x(n)}$ ${\displaystyle p}$ ${\displaystyle w(n)}$

${\displaystyle x(n)=\sum _{i=1}^{p}A_{i}e^{jn\omega _{i}}+w(n)}$.

La densidad espectral de potencia de se compone de funciones de impulso además de la función de densidad espectral debida al ruido. ${\displaystyle x(n)}$ ${\displaystyle p}$

Los métodos más comunes para la estimación de frecuencias implican la identificación del subespacio de ruido para extraer estos componentes. Estos métodos se basan en la descomposición propia de la matriz de autocorrelación en un subespacio de señal y un subespacio de ruido. Una vez identificados estos subespacios, se utiliza una función de estimación de frecuencia para encontrar las frecuencias de los componentes del subespacio de ruido. Los métodos más populares de estimación de frecuencia basados ​​en el subespacio de ruido son el método de Pisarenko , el método de clasificación de señales múltiples (MUSIC), el método de vectores propios y el método de norma mínima.

El método de Pisarenko

${\displaystyle {\hat {P}}_{\text{PHD}}\left(e^{j\omega }\right)={\frac {1}{\left|\mathbf {e} ^{H}\mathbf {v} _{\text{min}}\right|^{2}}}}$

MÚSICA

${\displaystyle {\hat {P}}_{\text{MU}}\left(e^{j\omega }\right)={\frac {1}{\sum _{i=p+1}^{M}\left|\mathbf {e} ^{H}\mathbf {v} _{i}\right|^{2}}}}$,

Método de vectores propios

${\displaystyle {\hat {P}}_{\text{EV}}\left(e^{j\omega }\right)={\frac {1}{\sum _{i=p+1}^{M}{\frac {1}{\lambda _{i}}}\left|\mathbf {e} ^{H}\mathbf {v} _{i}\right|^{2}}}}$

Método de la norma mínima

${\displaystyle {\hat {P}}_{\text{MN}}\left(e^{j\omega }\right)={\frac {1}{\left|\mathbf {e} ^{H}\mathbf {a} \right|^{2}}};\ \mathbf {a} =\lambda \mathbf {P} _{n}\mathbf {u} _{1}}$

Ejemplo de cálculo

Supongamos que , de a es una serie temporal (tiempo discreto) con media cero. Supongamos que es una suma de un número finito de componentes periódicos (todas las frecuencias son positivas): ${\displaystyle x_{n}}$ ${\displaystyle n=0}$ ${\displaystyle N-1}$

${\displaystyle {\begin{aligned}x_{n}&=\sum _{k}A_{k}\sin(2\pi \nu _{k}n+\phi _{k})\\&=\sum _{k}A_{k}\left(\sin(\phi _{k})\cos(2\pi \nu _{k}n)+\cos(\phi _{k})\sin(2\pi \nu _{k}n)\right)\\&=\sum _{k}\left(\overbrace {a_{k}} ^{A_{k}\sin(\phi _{k})}\cos(2\pi \nu _{k}n)+\overbrace {b_{k}} ^{A_{k}\cos(\phi _{k})}\sin(2\pi \nu _{k}n)\right)\end{aligned}}}$

La varianza de es, para una función de media cero como la anterior, dada por ${\displaystyle x_{n}}$

${\displaystyle {\frac {1}{N}}\sum _{n=0}^{N-1}x_{n}^{2}.}$

Si estos datos fueran muestras tomadas de una señal eléctrica, esta sería su potencia promedio (la potencia es energía por unidad de tiempo, por lo que es análoga a la varianza si la energía es análoga al cuadrado de la amplitud).

Ahora, para simplificar, supongamos que la señal se extiende infinitamente en el tiempo, por lo que pasamos al límite como Si la potencia promedio está acotada, lo que casi siempre es el caso en la realidad, entonces existe el siguiente límite y es la varianza de los datos. ${\displaystyle N\to \infty .}$

${\displaystyle \lim _{N\to \infty }{\frac {1}{N}}\sum _{n=0}^{N-1}x_{n}^{2}.}$

Nuevamente, para simplificar, pasaremos al tiempo continuo y supondremos que la señal se extiende infinitamente en el tiempo en ambas direcciones. Entonces estas dos fórmulas se convierten en

${\displaystyle x(t)=\sum _{k}A_{k}\sin(2\pi \nu _{k}t+\phi _{k})}$

y

${\displaystyle \lim _{T\to \infty }{\frac {1}{2T}}\int _{-T}^{T}x(t)^{2}dt.}$

La raíz cuadrada media de es , por lo que la varianza de es Por lo tanto, la contribución a la potencia promedio de proveniente del componente con frecuencia es Todas estas contribuciones se suman a la potencia promedio de ${\displaystyle \sin }$ ${\displaystyle 1/{\sqrt {2}}}$ ${\displaystyle A_{k}\sin(2\pi \nu _{k}t+\phi _{k})}$ ${\displaystyle {\tfrac {1}{2}}A_{k}^{2}.}$ ${\displaystyle x(t)}$ ${\displaystyle \nu _{k}}$ ${\displaystyle {\tfrac {1}{2}}A_{k}^{2}.}$ ${\displaystyle x(t).}$

Entonces la potencia en función de la frecuencia es y su función de distribución estadística acumulativa será ${\displaystyle {\tfrac {1}{2}}A_{k}^{2},}$ ${\displaystyle S(\nu )}$

${\displaystyle S(\nu )=\sum _{k:\nu _{k}<\nu }{\frac {1}{2}}A_{k}^{2}.}$

${\displaystyle S}$es una función escalonada , monótonamente no decreciente. Sus saltos ocurren en las frecuencias de los componentes periódicos de , y el valor de cada salto es la potencia o varianza de ese componente. ${\displaystyle x}$

La varianza es la covarianza de los datos consigo mismos. Si ahora consideramos los mismos datos pero con un desfase de , podemos tomar la covarianza de con , y definirla como la función de autocorrelación de la señal (o datos) : ${\displaystyle \tau }$ ${\displaystyle x(t)}$ ${\displaystyle x(t+\tau )}$ ${\displaystyle c}$ ${\displaystyle x}$

${\displaystyle c(\tau )=\lim _{T\to \infty }{\frac {1}{2T}}\int _{-T}^{T}x(t)x(t+\tau )dt.}$

Si existe, es una función par de Si la potencia promedio está acotada, entonces existe en todas partes, es finita y está acotada por que es la potencia promedio o varianza de los datos. ${\displaystyle \tau .}$ ${\displaystyle c}$ ${\displaystyle c(0),}$

Se puede demostrar que se puede descomponer en componentes periódicos con los mismos períodos que : ${\displaystyle c}$ ${\displaystyle x}$

${\displaystyle c(\tau )=\sum _{k}{\frac {1}{2}}A_{k}^{2}\cos(2\pi \nu _{k}\tau ).}$

Se trata, de hecho, de la descomposición espectral de sobre las diferentes frecuencias, y está relacionada con la distribución de potencia de sobre las frecuencias: la amplitud de un componente de frecuencia de es su contribución a la potencia media de la señal. ${\displaystyle c}$ ${\displaystyle x}$ ${\displaystyle c}$

El espectro de potencia de este ejemplo no es continuo y, por lo tanto, no tiene derivada y, por lo tanto, esta señal no tiene una función de densidad espectral de potencia. En general, el espectro de potencia suele ser la suma de dos partes: un espectro de líneas como el de este ejemplo, que no es continuo y no tiene una función de densidad, y un residuo, que es absolutamente continuo y sí tiene una función de densidad.

Véase también

• Estimación espectral multidimensional
• Periodograma
• Especificaciones de firma
• Espectrograma
• Análisis de tiempo y frecuencia
• Representación tiempo-frecuencia
• Reducir la probabilidad
• Distribución de potencia espectral

Referencias

1. P Stoica y R Moses, Análisis espectral de señales, Prentice Hall, 2005.
2. Welch, PD (1967), "El uso de la transformada rápida de Fourier para la estimación de espectros de potencia: un método basado en el promedio temporal sobre periodogramas cortos modificados", IEEE Transactions on Audio and Electroacoustics , AU-15 (2): 70–73, Bibcode :1967ITAE...15...70W, doi :10.1109/TAU.1967.1161901, S2CID  13900622
3. Stoica, Petre; Babu, Prabhu; Li, Jian (enero de 2011). "Nuevo método de estimación de parámetros dispersos en modelos separables y su uso para el análisis espectral de datos muestreados irregularmente". IEEE Transactions on Signal Processing . 59 (1): 35–47. Bibcode :2011ITSP...59...35S. doi :10.1109/TSP.2010.2086452. ISSN  1053-587X. S2CID  15936187.
4. Stoica, Petre; Li, Jian; Ling, Jun; Cheng, Yubo (abril de 2009). "Recuperación de datos faltantes mediante un enfoque adaptativo iterativo no paramétrico". Conferencia internacional IEEE de 2009 sobre acústica, habla y procesamiento de señales . IEEE. págs. 3369–3372. doi :10.1109/icassp.2009.4960347. ISBN . 978-1-4244-2353-8.
5. Sward, Johan; Adalbjornsson, Stefan Ingi; Jakobsson, Andreas (marzo de 2017). "Una generalización del estimador iterativo disperso basado en la covarianza". Conferencia internacional IEEE de 2017 sobre acústica, habla y procesamiento de señales (ICASSP) . IEEE. págs. 3954–3958. doi :10.1109/icassp.2017.7952898. ISBN . 978-1-5090-4117-6. Número de identificación del sujeto  5640068.
6. Yardibi, Tarik; Li, Jian; Stoica, Petre; Xue, Ming; Baggeroer, Arthur B. (enero de 2010). "Localización y detección de fuentes: un enfoque adaptativo iterativo no paramétrico basado en mínimos cuadrados ponderados". IEEE Transactions on Aerospace and Electronic Systems . 46 (1): 425–443. Bibcode :2010ITAES..46..425Y. doi :10.1109/TAES.2010.5417172. hdl : 1721.1/59588 . ISSN  0018-9251. S2CID  18834345.
7. Panahi, Ashkan; Viberg, Mats (febrero de 2011). "Sobre la resolución del método de estimación de DOA basado en LASSO". Taller internacional ITG de 2011 sobre antenas inteligentes. IEEE. págs. 1–5. doi :10.1109/wsa.2011.5741938. ISBN . 978-1-61284-075-8. Número de identificación del sujeto  7013162.
8. Percival, Donald B.; Walden, Andrew T. (1992). Análisis espectral para aplicaciones físicas . Cambridge University Press. ISBN 9780521435413.
9. Burg, JP (1967) "Análisis espectral de máxima entropía", Actas de la 37.ª Reunión de la Sociedad de Geofísicos de Exploración , Oklahoma City, Oklahoma.
10. Hayes, Monson H., Procesamiento y modelado estadístico de señales digitales , John Wiley & Sons, Inc., 1996. ISBN 0-471-59431-8 . 
11. Lerga, Jonatan. "Descripción general de los métodos de estimación de frecuencia instantánea de señales" (PDF) . Universidad de Rijeka . Consultado el 22 de marzo de 2014 .

Lectura adicional

• Porat, B. (1994). Procesamiento digital de señales aleatorias: teoría y métodos . Prentice Hall. ISBN 978-0-13-063751-2.
• Priestley, MB (1991). Análisis espectral y series temporales . Academic Press. ISBN 978-0-12-564922-3.

• Stoica, P.; Moses, R. (2005). Análisis espectral de señales . Prentice Hall. ISBN 978-0-13-113956-5.

• Thomson, DJ (1982). "Estimación del espectro y análisis armónico". Actas del IEEE . 70 (9): 1055–1096. Código Bibliográfico :1982IEEEP..70.1055T. CiteSeerX  10.1.1.471.1278 . doi :10.1109/PROC.1982.12433. S2CID  290772.