Punto umbilical

Líneas de curvatura en un elipsoide que muestran puntos umbilicales (rojo).

En la geometría diferencial de superficies en tres dimensiones, los umbilicales son puntos de una superficie que son localmente esféricos. En dichos puntos las curvaturas normales en todas las direcciones son iguales, por lo tanto, ambas curvaturas principales son iguales y cada vector tangente es una dirección principal . El nombre "umbilical" proviene del latín umbilicus ( ombligo ).

Los puntos umbilicales generalmente aparecen como puntos aislados en la región elíptica de la superficie; es decir, donde la curvatura gaussiana es positiva.

Problema sin resolver en matemáticas :

¿Toda esfera topológica suave en el espacio euclidiano tiene al menos dos umbilicales?

(más problemas sin resolver en matemáticas)

La esfera es la única superficie con curvatura distinta de cero donde cada punto es umbilical. Un umbilical plano es un umbilical con curvatura gaussiana cero. La silla de montar de mono es un ejemplo de superficie con un umbilical plano y en el plano cada punto es un umbilical plano. Una superficie cerrada topológicamente equivalente a un toro puede tener o no umbilicales cero, pero toda superficie cerrada de característica de Euler distinta de cero , incrustada suavemente en el espacio euclidiano , tiene al menos un umbilical. Una conjetura no demostrada de Constantin Carathéodory afirma que toda superficie lisa topológicamente equivalente a la esfera tiene al menos dos umbilicales. ^[1]

Los tres tipos principales de puntos umbilicales son los umbilicales elípticos, los umbilicales parabólicos y los umbilicales hiperbólicos. Los umbilicales elípticos tienen tres líneas de cresta que pasan por el umbilical y los umbilicales hiperbólicos tienen solo una. Los umbilicales parabólicos son un caso transicional con dos crestas, una de las cuales es singular. Otras configuraciones son posibles para los casos transicionales. Estos casos corresponden a las catástrofes elementales D ₄ ⁻ , D ₅ y D ₄ ^{+ de} la teoría de catástrofes de René Thom .

Los umbilicales también se pueden caracterizar por el patrón del campo vectorial de dirección principal alrededor del umbilical, que normalmente forma una de tres configuraciones: estrella, limón y estrella-limón (o estrella-monstar). El índice del campo vectorial es −½ (estrella) o ½ (limón, estrella-monstar). Los umbilicales elípticos y parabólicos siempre tienen el patrón de estrella, mientras que los umbilicales hiperbólicos pueden ser estrella, limón o estrella-monstar. Esta clasificación se debió por primera vez a Darboux y los nombres provienen de Hannay. ^[2]

Para superficies de género 0 con umbilicales aislados, por ejemplo, un elipsoide, el índice del campo de vectores de dirección principal debe ser 2 según el teorema de Poincaré-Hopf . Las superficies de género 0 genérico tienen al menos cuatro umbilicales de índice ½. Un elipsoide de revolución tiene dos umbilicales no genéricos, cada uno de los cuales tiene índice 1. ^[3]

• Configuraciones de líneas de curvatura cerca de los cordones umbilicales.
• 
  Estrella
• 
  Monstruo
• 
  Limón

Clasificación de los cordones umbilicales

Formas cúbicas

La clasificación de los umbilicales está estrechamente vinculada a la clasificación de las formas cúbicas reales . Una forma cúbica tendrá un número de líneas de raíz tal que la forma cúbica sea cero para todos los reales . Hay varias posibilidades, entre ellas: ${\displaystyle ax^{3}+3bx^{2}y+3cxy^{2}+dy^{3}}$ ${\displaystyle \lambda (x,y)}$ ${\displaystyle \lambda }$

• Tres líneas distintas: una forma cúbica elíptica , modelo estándar . ${\displaystyle x^{2}y-y^{3}}$
• Tres líneas, dos de las cuales coincidentes: forma cúbica parabólica , modelo estándar . ${\displaystyle x^{2}y}$
• Una sola recta real: forma cúbica hiperbólica , modelo estándar . ${\displaystyle x^{2}y+y^{3}}$
• Tres líneas coincidentes, modelo estándar . ^[4] ${\displaystyle x^{3}}$

Las clases de equivalencia de tales cúbicas bajo escalamiento uniforme forman un espacio proyectivo real tridimensional y el subconjunto de formas parabólicas define una superficie, llamada brazalete umbilical por Christopher Zeeman . ^[4] Tomar clases de equivalencia bajo rotación del sistema de coordenadas elimina un parámetro adicional y las formas cúbicas pueden representarse mediante la forma cúbica compleja con un solo parámetro complejo . Las formas parabólicas ocurren cuando , el deltoides interno, las formas elípticas están dentro del deltoides y la hiperbólica afuera. Si y no es una raíz cúbica de la unidad, entonces la forma cúbica es una forma cúbica en ángulo recto que juega un papel especial para las umbilicales. Si entonces dos de las líneas de la raíz son ortogonales. ^[5] ${\displaystyle z^{3}+3{\overline {\beta }}z^{2}{\overline {z}}+3\beta z{\overline {z}}^{2}+{\overline {z}}^{3}}$ ${\displaystyle \beta }$ ${\displaystyle \beta ={\tfrac {1}{3}}(2e^{i\theta }+e^{-2i\theta })}$ ${\displaystyle \left|\beta \right|=1}$ ${\displaystyle \beta }$ ${\displaystyle \left|\beta \right|={\tfrac {1}{3}}}$

Una segunda forma cúbica, la jacobiana, se forma tomando el determinante jacobiano de la función de valor vectorial , . Hasta un múltiplo constante, esta es la forma cúbica . Si se utilizan números complejos, la jacobiana es una forma cúbica parabólica cuando , el deltoide externo en el diagrama de clasificación. ^[5] ${\displaystyle F:\mathbb {R} ^{2}\rightarrow \mathbb {R} ^{2}}$ ${\displaystyle F(x,y)=(x^{2}+y^{2},ax^{3}+3bx^{2}y+3cxy^{2}+dy^{3})}$ ${\displaystyle bx^{3}+(2c-a)x^{2}y+(d-2b)xy^{2}-cy^{3}}$ ${\displaystyle \beta =-2e^{i\theta }-e^{-2i\theta }}$

Clasificación umbilical

Clasificación umbilical, el plano —. El deltoides interno da umbilicales parabólicos, separa umbilicales elípticos e hiperbólicos. Cúspides en el deltoides interno: umbilicales cúbicos. Círculo externo, el nacimiento de umbilicales separa configuraciones de estrella y monstar. Deltoides externo, separa configuración monstar y limón. Diagonales y la línea horizontal: umbilicales simétricos con simetría especular. ${\displaystyle \beta }$

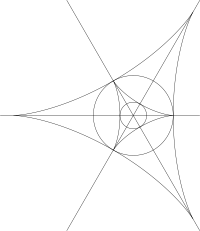
Cualquier superficie con un punto umbilical aislado en el origen puede expresarse como una parametrización de forma Monge , donde es la curvatura principal única. El tipo de umbilical se clasifica por la forma cúbica de la parte cúbica y la forma cúbica jacobiana correspondiente. Si bien las direcciones principales no están definidas de manera única en un umbilical, se pueden encontrar los límites de las direcciones principales al seguir una cresta en la superficie y estos corresponden a las líneas de raíz de la forma cúbica. El patrón de líneas de curvatura está determinado por el jacobiano. ^[5] ${\displaystyle z={\tfrac {1}{2}}\kappa (x^{2}+y^{2})+{\tfrac {1}{3}}(ax^{3}+3bx^{2}y+3cxy^{2}+dy^{3})+\ldots }$ ${\displaystyle \kappa }$

La clasificación de los puntos umbilicales es la siguiente: ^[5]

• Deltoides interno interior - umbilicales elípticos
  • En el círculo interior: dos líneas de cresta tangentes
• Sobre el deltoides interno: umbilicales parabólicos
• Deltoides externo interno - umbilicales hiperbólicos
  • Círculo interior exterior: patrón de estrella
  • En el círculo exterior: nacimiento de los cordones umbilicales
  • Entre el círculo exterior y el deltoides exterior: patrón Monstar
  • Deltoides externo externo: patrón de limón
• Cúspides del deltoides interno: umbilicales cúbicos (simbólicos)
• En las diagonales y la línea horizontal: umbilicales simétricos con simetría especular

En una familia genérica de superficies, los umbilicales pueden crearse o destruirse en pares: el nacimiento de los umbilicales es una transición. Ambos umbilicales serán hiperbólicos, uno con un patrón de estrella y otro con un patrón de estrella gigante. El círculo exterior del diagrama, una forma cúbica de ángulo recto, da estos casos de transición. Los umbilicales simbólicos son un caso especial de esto. ^[5]

Superficie focal

Una superficie con un umbilical elíptico y su superficie focal.

Una superficie con un umbilical hiperbólico y su superficie focal.

Los umbilicales elípticos y los umbilicales hiperbólicos tienen superficies focales claramente diferentes . Una cresta en la superficie corresponde a los bordes cuspidales, por lo que cada lámina de la superficie focal elíptica tendrá tres bordes cuspidales que se unen en el foco umbilical y luego cambian a la otra lámina. En el caso de un umbilical hiperbólico, hay un solo borde cuspidales que cambian de una lámina a la otra. ^[5]

Definición en dimensión superior en variedades de Riemann

Un punto p en una subvariedad de Riemann es umbilical si, en p , la Segunda forma fundamental (con valores vectoriales) es algún tensor vectorial normal la métrica inducida ( Primera forma fundamental ). De manera equivalente, para todos los vectores U ,  V en p , II( U ,  V ) =  g _p ( U ,  V ) , donde es el vector de curvatura media en  p . ${\displaystyle \nu }$ ${\displaystyle \nu }$

Se dice que una subvariedad es umbílica (o totalmente umbílica) si esta condición se cumple en cada punto "p". Esto equivale a decir que la subvariedad puede volverse totalmente geodésica mediante un cambio conforme apropiado de la métrica de la variedad circundante ("ambiente"). Por ejemplo, una superficie en el espacio euclidiano es umbílica si y solo si es un trozo de una esfera.

Véase también

• umbilical – término anatómico que significa o está relacionado con el ombligo

Referencias

1. Berger, Marcel (2010), "La conjetura de Caradéodory", Geometría revelada , Springer, Heidelberg, págs. 389-390, doi :10.1007/978-3-540-70997-8, ISBN 978-3-540-70996-1, Sr.  2724440.
2. Berry, MV; Hannay, JH (1977). "Puntos umbilicales en superficies aleatorias gaussianas". J. Phys. A . 10 (11): 1809–21. Código Bibliográfico :1977JPhA...10.1809B. doi :10.1088/0305-4470/10/11/009.
3. Porteous, pág. 208
4. Poston, Tim ; Stewart, Ian (1978), Teoría de catástrofes y sus aplicaciones , Pitman, ISBN 0-273-01029-8
5. Porteous, Ian R. (2001), Diferenciación geométrica , Cambridge University Press, págs. 198-213, ISBN 0-521-00264-8

• Darboux, Gaston (1896) [1887], Leçons sur la théorie génerale des Surfaces: Volúmenes I-IV , Gauthier-Villars
  • Volumen I
  • Volumen II
  • Volumen III
  • Volumen IV
• Imágenes de estrella, limón, monstar y otras referencias