Segundo momento polar del área

Cantidad de resistencia a la deformación torsional

El segundo momento polar de área , también conocido (incorrectamente, coloquialmente) como "momento polar de inercia" o incluso "momento de inercia", es una cantidad utilizada para describir la resistencia a la deformación torsional ( deflexión ), en objetos (o segmentos de un objeto) con una sección transversal invariante y sin deformación significativa o deformación fuera del plano. ^[1] Es un constituyente del segundo momento de área , vinculado a través del teorema del eje perpendicular . Donde el segundo momento de área planar describe la resistencia de un objeto a la deflexión ( flexión ) cuando se somete a una fuerza aplicada a un plano paralelo al eje central, el segundo momento polar de área describe la resistencia de un objeto a la deflexión cuando se somete a un momento aplicado en un plano perpendicular al eje central del objeto (es decir, paralelo a la sección transversal). Similar a los cálculos del segundo momento de área planar ( , , y ), el segundo momento polar de área a menudo se denota como . Si bien varios libros de texto de ingeniería y publicaciones académicas también lo denominan o , se debe prestar especial atención a esta designación para que no se confunda con la constante de torsión , , utilizada para objetos no cilíndricos. ${\displaystyle I_{x}}$ ${\displaystyle I_{y}}$ ${\displaystyle I_{xy}}$ ${\displaystyle I_{z}}$ ${\displaystyle J}$ ${\displaystyle J_{z}}$ ${\displaystyle J_{t}}$

En términos simples, el momento polar de área es la resistencia de un eje o viga a ser distorsionado por torsión, en función de su forma. La rigidez proviene únicamente del área de la sección transversal del objeto y no depende de su composición material o módulo de corte . Cuanto mayor sea la magnitud del segundo momento polar de área, mayor será la rigidez torsional del objeto.

Definición

Esquema que muestra cómo se calcula el segundo momento polar del área para una forma arbitraria en torno a un eje . Donde es la distancia radial al elemento . ${\displaystyle O}$ ${\displaystyle \rho }$ ${\displaystyle dA}$

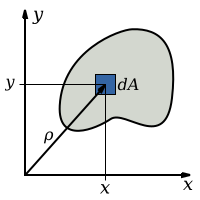
La ecuación que describe el momento polar del área es una integral múltiple sobre el área de la sección transversal, , del objeto. ${\displaystyle A}$

$${\displaystyle J=\iint _{A}r^{2}\,dA}$$¿Dónde está la distancia al elemento ? ${\displaystyle r}$ ${\displaystyle dA}$

Sustituyendo los componentes y , utilizando el teorema de Pitágoras : ${\displaystyle x}$ ${\displaystyle y}$ $${\displaystyle J=\iint _{A}\left(x^{2}+y^{2}\right)dx\,dy}$$ $${\displaystyle J=\iint _{A}x^{2}\,dx\,dy+\iint _{A}y^{2}\,dx\,dy}$$

Dadas las ecuaciones de segundo momento de área plana , donde: $${\displaystyle I_{x}=\iint _{A}y^{2}dx\,dy}$$ $${\displaystyle I_{y}=\iint _{A}x^{2}dx\,dy}$$

Se muestra que el momento polar del área se puede describir como la suma de los momentos de área planos y polares, y ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle I_{x}}$ ${\displaystyle I_{y}}$ $${\displaystyle \therefore J=I_{z}=I_{x}+I_{y}}$$

Esto también se muestra en el teorema del eje perpendicular . ^[2] Para objetos que tienen simetría rotacional, ^[3] como un cilindro o un tubo hueco, la ecuación se puede simplificar a: o $${\displaystyle J=2I_{x}}$$ $${\displaystyle J=2I_{y}}$$

Para una sección circular con radio : ${\displaystyle R}$ $${\displaystyle I_{z}=\int _{0}^{2\pi }\int _{0}^{R}r^{2}(r\,dr\,d\phi )={\frac {\pi R^{4}}{2}}}$$

Unidad

La unidad SI para el segundo momento de área polar , al igual que el segundo momento de área planar ^, es metros a la cuarta potencia ( m4 ) y pulgadas a la cuarta potencia ( in4 ) en unidades tradicionales de EE. UU. ^y unidades imperiales .

Limitaciones

El segundo momento polar de área puede ser insuficiente para su uso en el análisis de vigas y ejes con secciones transversales no circulares, debido a su tendencia a deformarse cuando se tuercen, lo que provoca deformaciones fuera del plano. En tales casos, se debe sustituir por una constante de torsión , donde se incluye una constante de deformación adecuada para compensar el efecto de deformación. Dentro de esto, hay artículos que diferencian entre el segundo momento polar de área , , y la constante de torsión , , que ya no se utiliza para describir el segundo momento polar de área. ^[4] ${\displaystyle I_{z}}$ ${\displaystyle J_{t}}$ ${\displaystyle J}$

En el caso de objetos con una variación significativa de la sección transversal (a lo largo del eje del par aplicado), que no se pueden analizar en segmentos, puede ser necesario utilizar un enfoque más complejo. Véase elasticidad 3D .

Solicitud

Aunque el segundo momento polar del área se utiliza con mayor frecuencia para calcular el desplazamiento angular de un objeto sometido a un momento ( torque ) aplicado en paralelo a la sección transversal, el valor de rigidez proporcionado no tiene ninguna relación con la resistencia torsional proporcionada a un objeto como función de sus materiales constituyentes. La rigidez proporcionada por el material de un objeto es una característica de su módulo de corte , . Combinando estas dos características con la longitud del eje, , se puede calcular la deflexión angular de un eje, , debido al torque aplicado, : ${\displaystyle G}$ ${\displaystyle L}$ ${\displaystyle \theta }$ ${\displaystyle T}$ $${\displaystyle \theta ={\frac {TL}{JG}}}$$

Como se muestra, cuanto mayor sea el módulo de corte y el momento polar del área del material (es decir, mayor área de la sección transversal), mayor será la resistencia a la deflexión torsional.

El segundo momento polar del área aparece en las fórmulas que describen la tensión de torsión y el desplazamiento angular.

Esfuerzos de torsión: donde es el esfuerzo cortante de torsión, es el par aplicado, es la distancia desde el eje central y es el segundo momento polar del área. $${\displaystyle \tau ={\frac {T\,r}{J_{z}}}}$$ ${\displaystyle \tau }$ ${\displaystyle T}$ ${\displaystyle r}$ ${\displaystyle J_{z}}$

Nota: En un eje circular, la tensión cortante es máxima en la superficie del eje.

Ejemplo de cálculo

El rotor de una turbina de vapor moderna .

Cálculo del radio del eje de una turbina de vapor para un turbogrupo:

Supuestos:

• La potencia transportada por el eje es de 1000 MW , lo que es típico para una gran central nuclear . 
• La tensión de fluencia del acero utilizado para fabricar el eje ( τ _{límite elástico} ) es: 250  ×  10 ⁶  N/m ² .
• La electricidad tiene una frecuencia de 50 Hz , que es la frecuencia típica en Europa. En América del Norte, la frecuencia es de 60 Hz. Esto se hace suponiendo que existe una correlación 1:1 entre la velocidad de rotación de la turbina y la frecuencia de la red eléctrica.  

La frecuencia angular se puede calcular con la siguiente fórmula: $${\displaystyle \omega =2\pi f}$$

El par transportado por el eje está relacionado con la potencia mediante la siguiente ecuación: $${\displaystyle P=T\omega }$$

Por tanto, la frecuencia angular es 314,16 rad / s y el par 3,1831 × 10 ⁶ N·m .    

El par máximo es: $${\displaystyle T_{\max }={\frac {\tau _{\max }J_{z}}{r}}}$$

Después de sustituir el segundo momento polar del área se obtiene la siguiente expresión: $${\displaystyle r={\sqrt[{3}]{\frac {2T_{\max }}{\pi \tau _{\max }}}}}$$

El radio es r = 0,200  m = 200  mm, o un diámetro de 400  mm. Si se añade un factor de seguridad de 5 y se vuelve a calcular el radio con la tensión admisible igual a τ _adm = τ _fluencia /5, el resultado es un radio de 0,343  m, o un diámetro de 690  mm, el tamaño aproximado del eje de un turborreactor de una central nuclear.

Comparación de segundos momentos polares de área y momentos de inercia (segundos momentos de masa)

Cilindro hueco

Segundo momento polar del área: $${\displaystyle I_{z}={\frac {\pi \left(D^{4}-d^{4}\right)}{32}}}$$

Momento de inercia: $${\displaystyle I_{c}=I_{z}\rho l={\frac {\pi \rho l\left(D^{4}-d^{4}\right)}{64}}}$$

Cilindro macizo

Segundo momento polar del área $${\displaystyle I_{z}={\frac {\pi D^{4}}{32}}}$$

Momento de inercia donde: $${\displaystyle I_{c}=I_{z}\rho l={\frac {\pi \rho lD^{4}}{64}}}$$

• ${\displaystyle d}$es el diámetro interior en metros (m)
• ${\displaystyle D}$es el diámetro exterior en metros (m)
• ${\displaystyle I_{c}}$es el momento de inercia en kg· ^m2
• ${\displaystyle I_{z}}$es el segundo momento polar del área en metros a la cuarta potencia (m ⁴ )
• ${\displaystyle l}$es la longitud del cilindro en metros (m)
• ${\displaystyle \rho }$es la masa específica en kg/ ^m3

Véase también

• Constante de torsión
• Resorte de torsión
• Suspensión de barra de torsión
• Segundo momento del área
• Módulo de corte
• Lista de segundos momentos del área

Referencias

1. Ugural AC, Fenster SK. Resistencia avanzada y elasticidad aplicada. 3.ª edición. Prentice-Hall Inc. Englewood Cliffs, NJ. 1995. ISBN  0-13-137589-X .
2. "Momento de inercia; definición con ejemplos". www.efunda.com .
3. Obregón, Joaquín (2012). Simetría mecánica. Autor: Casa. ISBN 978-1-4772-3372-6.
4. galtor. "¿Cuál es la diferencia entre el momento polar de área ("momento polar de inercia"), IPIP y la constante de torsión, JTJT de una sección transversal?".

Enlaces externos

• Torsión de ejes - engineeringtoolbox.com
• Propiedades elásticas y módulo de Young para algunos materiales - engineeringtoolbox.com
• Base de datos de propiedades de materiales - matweb.com