En la geometría de las teselaciones , una tesela de reptil o reptil es una forma que se puede diseccionar en copias más pequeñas de la misma forma. El término fue acuñado como un juego de palabras con los reptiles animales por el matemático recreativo Solomon W. Golomb y popularizado por Martin Gardner en su columna " Juegos matemáticos " en la edición de mayo de 1963 de Scientific American . [1] En 2012, Lee Sallows introdujo una generalización de las tesela de reptil llamadas conjuntos de tesela autoensamblable en Mathematics Magazine . [2]
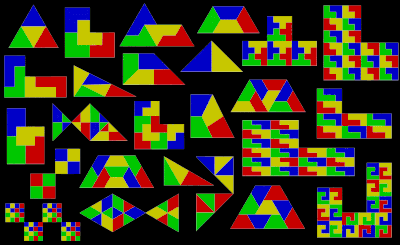
Una tesela de reptil se etiqueta como rep- n si la disección utiliza n copias. Tal forma necesariamente forma la tesela prototípica para un teselado del plano, en muchos casos un teselado aperiódico . Una disección de tesela de reptil que utiliza diferentes tamaños de la forma original se llama tesela de reptil irregular o irreptil. Si la disección utiliza n copias, se dice que la forma es irrep- n . Si todas estas subteselas son de diferentes tamaños, entonces el teselado se describe además como perfecto. Una forma que es rep- n o irrep- n es trivialmente también irrep-( kn − k + n ) para cualquier k > 1, al reemplazar la tesela más pequeña en la disección rep- n por n tesela aún más pequeña. El orden de una forma, ya sea que utilice tesela de reptil o tesela de irrep, es el menor número posible de tesela que será suficiente. [3]
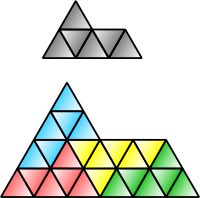
Todo cuadrado , rectángulo , paralelogramo , rombo o triángulo tiene una superficie de rep-4. El hexágono de la esfinge (ilustrado arriba) tiene una superficie de rep-4 y rep-9, y es uno de los pocos pentágonos autorreplicantes conocidos. La isla de Gosper tiene una superficie de rep-7. El copo de nieve de Koch tiene una superficie de irrep-7: seis copos de nieve pequeños del mismo tamaño, junto con otro copo de nieve con un área tres veces mayor que los más pequeños, pueden combinarse para formar un único copo de nieve más grande.
Un triángulo rectángulo con lados en razón de 1:2 es rep-5, y su disección rep-5 forma la base del mosaico aperiódico en rueda de molino . Según el teorema de Pitágoras , la hipotenusa , o lado inclinado del triángulo rep-5, tiene una longitud de √ 5 .
La norma internacional ISO 216 define los tamaños de las hojas de papel utilizando el √ 2 , en el que el lado largo de una hoja de papel rectangular es la raíz cuadrada de dos veces el lado corto del papel. Los rectángulos con esta forma son rep-2. Un rectángulo (o paralelogramo) es rep- n si su relación de aspecto es √ n :1. Un triángulo rectángulo isósceles también es rep-2.
Algunas figuras de reptiles, como el cuadrado y el triángulo equilátero , son simétricas y permanecen idénticas cuando se reflejan en un espejo . Otras, como la esfinge , son asimétricas y existen en dos formas distintas relacionadas por la reflexión especular. La disección de la esfinge y algunas otras figuras de reptiles asimétricas requiere el uso tanto de la forma original como de su imagen especular.
Algunas piezas de reptiles se basan en poliformas como polidiamantes y poliominós , o formas creadas al colocar triángulos equiláteros y cuadrados borde con borde.
Si un poliominó es rectificable, es decir, capaz de formar mosaicos en un rectángulo , entonces también será un mosaico de rep, porque el rectángulo tendrá una razón de longitud de lado entera y, por lo tanto, formará mosaicos en un cuadrado . Esto se puede ver en los octominós , que se crean a partir de ocho cuadrados. Dos copias de algunos octominós formarán mosaicos en un cuadrado; por lo tanto, estos octominós también son mosaicos de rep de 16.
Cuatro copias de algunos nonominós y nonarreyes formarán un cuadrado, por lo tanto, estas poliformas también son rep-tiles de 36 réplicas.
De manera similar, si un polidiamante cubre un triángulo equilátero, también será un mosaico de reptil.
Un triángulo rectángulo es un triángulo que contiene un ángulo recto de 90°. Dos formas particulares de triángulo rectángulo han atraído la atención de los investigadores de reptiles: el triángulo de 45°-90°-45° y el triángulo de 30°-60°-90°.
Las poliformas basadas en triángulos rectángulos isósceles , con lados en la razón 1 : 1 : √ 2 , se conocen como poliábolos . Un número infinito de ellos son rep-tiles. De hecho, el más simple de todos los rep-tiles es un solo triángulo rectángulo isósceles. Es rep-2 cuando se divide por una sola línea que biseca el ángulo recto con la hipotenusa . Rep-2 rep-tiles también son rep-2 n y los triángulos rep-4,8,16+ producen más rep-tiles. Estos se encuentran descartando la mitad de las subcopias y permutando el resto hasta que sean simétricos en espejo dentro de un triángulo rectángulo. En otras palabras, dos copias formarán un triángulo rectángulo. Uno de estos nuevos rep-tiles recuerda al pez formado a partir de tres triángulos equiláteros .
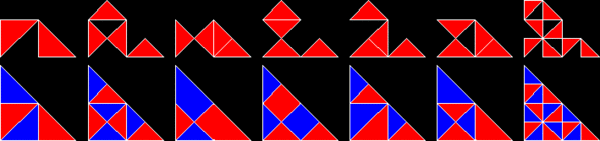
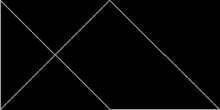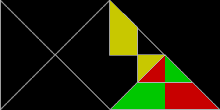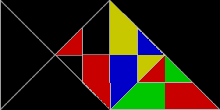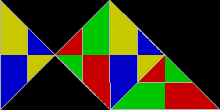
Las poliformas basadas en triángulos rectángulos de 30°-60°-90°, con lados en la proporción 1 : √ 3 : 2, se conocen como polidrafts . Algunas son idénticas a los polidiamantes . [4]
Muchos de los rep-tiles comunes son rep- n 2 para todos los valores enteros positivos de n . En particular, esto es cierto para tres trapecios , incluido el formado a partir de tres triángulos equiláteros, para tres hexágonos paralelos al eje (el L-trominó, el L-tetrominó y el P-pentominó) y el hexágono esfinge. [5] Además, muchos rep-tiles, particularmente aquellos con mayor rep- n , pueden auto-teselarse de diferentes maneras. Por ejemplo, el rep-9 L-tetraminó tiene al menos catorce rep-tiles diferentes. El hexágono esfinge rep-9 también puede teselarse de diferentes maneras.
Los rep-tiles más conocidos son polígonos con un número finito de lados, pero algunas formas con un número infinito de lados también pueden ser rep-tiles. Por ejemplo, el triángulo teragónico , o triángulo con cuernos, es rep-4. También es un ejemplo de un rep-tile fractal.
Las reptiletas triangulares y cuadriláteras (de cuatro lados) son comunes, pero las reptiletas pentagonales son raras. Durante mucho tiempo, se creyó ampliamente que la esfinge era el único ejemplo conocido, pero el matemático alemán / neozelandés Karl Scherer y el matemático estadounidense George Sicherman han encontrado más ejemplos, incluida una pirámide doble y una versión alargada de la esfinge. Estas reptiletas pentagonales están ilustradas en las páginas de Math Magic supervisadas por el matemático estadounidense Erich Friedman . [6] Sin embargo, la esfinge y sus versiones extendidas son los únicos pentágonos conocidos que pueden reptilearse con copias iguales. Consulte las páginas de reptiles de Clarke.
Los mosaicos de reptiles se pueden utilizar para crear fractales o formas que son autosimilares en escalas cada vez más pequeñas. Un fractal de mosaico de reptiles se forma subdividiendo el mosaico de reptiles, eliminando una o más copias de la forma subdividida y luego continuando de forma recursiva . Por ejemplo, la alfombra de Sierpinski se forma de esta manera a partir de un mosaico de reptiles de un cuadrado en 27 cuadrados más pequeños, y el triángulo de Sierpinski se forma a partir de un mosaico de reptiles de un triángulo equilátero en cuatro triángulos más pequeños. Cuando se descarta una subcopia, se puede utilizar un L- triominó de reptiles-4 para crear cuatro fractales, dos de los cuales son idénticos excepto por la orientación .
Como los fractales suelen ser autosimilares en escalas cada vez más pequeñas, muchos pueden descomponerse en copias de sí mismos como un mosaico de reptiles. Sin embargo, si el fractal tiene un interior vacío , esta descomposición puede no conducir a un mosaico de todo el plano. Por ejemplo, el triángulo de Sierpinski es rep-3, mosaico con tres copias de sí mismo, y la alfombra de Sierpinski es rep-8, mosaico con ocho copias de sí misma, pero la repetición de estas descomposiciones no forma un mosaico. Por otro lado, la curva del dragón es una curva que llena el espacio con un interior no vacío; es rep-4, y forma un mosaico. De manera similar, la isla de Gosper es rep-7, formada a partir de la curva de Gosper que llena el espacio, y nuevamente forma un mosaico.
Por construcción, cualquier fractal definido por un sistema de funciones iteradas de n mapas contráctiles de la misma proporción es rep-n.
Entre los polígonos regulares, sólo el triángulo y el cuadrado pueden diseccionarse en copias más pequeñas de sí mismos de igual tamaño. Sin embargo, un hexágono regular puede diseccionarse en seis triángulos equiláteros, cada uno de los cuales puede diseccionarse en un hexágono regular y tres triángulos equiláteros más. Esta es la base para una teselación infinita del hexágono con hexágonos. El hexágono es, por lo tanto, un irrep-∞ o irrep-infinito.
![Copo de nieve de Koch fractal alargado (siamés) revestido con infinitas copias de sí mismo[7]](http://upload.wikimedia.org/wikipedia/commons/thumb/2/29/Frattale_infinito_rep-tile.gif/1280px-Frattale_infinito_rep-tile.gif)
