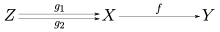
En el contexto del álgebra abstracta o del álgebra universal , un monomorfismo es un homomorfismo inyectivo . Un monomorfismo de X a Y se suele denotar con la notación .
En el contexto más general de la teoría de categorías , un monomorfismo (también llamado morfismo mónico o mono ) es un morfismo cancelativo por la izquierda . Es decir, una flecha f : X → Y tal que para todos los objetos Z y todos los morfismos g 1 , g 2 : Z → X ,
Los monomorfismos son una generalización categórica de funciones inyectivas (también llamadas "funciones uno a uno"); en algunas categorías las nociones coinciden, pero los monomorfismos son más generales, como en los ejemplos siguientes.
En el contexto de los conjuntos parciales, las intersecciones son idempotentes : la intersección de cualquier cosa consigo misma es ella misma. Los monomorfismos generalizan esta propiedad a categorías arbitrarias. Un morfismo es un monomorfismo si es idempotente con respecto a los pullbacks .
El dual categórico de un monomorfismo es un epimorfismo , es decir, un monomorfismo en una categoría C es un epimorfismo en la categoría dual C op . Toda sección es un monomorfismo, y toda retracción es un epimorfismo.
Los morfismos invertibles por la izquierda son necesariamente mónicos: si l es un inverso por la izquierda para f (lo que significa que l es un morfismo y ), entonces f es mónico, como
Un morfismo invertible por la izquierda se llama mono dividido o sección .
Sin embargo, un monomorfismo no necesariamente debe ser invertible por la izquierda. Por ejemplo, en la categoría Grupo de todos los grupos y homomorfismos de grupos entre ellos, si H es un subgrupo de G entonces la inclusión f : H → G es siempre un monomorfismo; pero f tiene un inverso por la izquierda en la categoría si y solo si H tiene un complemento normal en G .
Un morfismo f : X → Y es mónico si y sólo si la función inducida f ∗ : Hom( Z , X ) → Hom( Z , Y ) , definida por f ∗ ( h ) = f ∘ h para todos los morfismos h : Z → X , es inyectiva para todos los objetos Z .
Todo morfismo en una categoría concreta cuya función subyacente es inyectiva es un monomorfismo; en otras palabras, si los morfismos son en realidad funciones entre conjuntos, entonces cualquier morfismo que sea una función biunívoca será necesariamente un monomorfismo en el sentido categórico. En la categoría de conjuntos también se cumple el recíproco, por lo que los monomorfismos son exactamente los morfismos inyectivos . El recíproco también se cumple en la mayoría de las categorías naturales de álgebras debido a la existencia de un objeto libre en un generador. En particular, es cierto en las categorías de todos los grupos, de todos los anillos y en cualquier categoría abeliana .
No es cierto, sin embargo, en general que todos los monomorfismos deban ser inyectivos en otras categorías; es decir, hay entornos en los que los morfismos son funciones entre conjuntos, pero se puede tener una función que no sea inyectiva y, sin embargo, sea un monomorfismo en el sentido categórico. Por ejemplo, en la categoría Div de grupos divisibles (abelianos) y homomorfismos de grupo entre ellos hay monomorfismos que no son inyectivos: considérese, por ejemplo, la función cociente q : Q → Q / Z , donde Q son los racionales bajo adición, Z los enteros (también considerados un grupo bajo adición), y Q / Z es el grupo cociente correspondiente . Esta no es una función inyectiva, ya que, por ejemplo, todo entero se mapea a 0. Sin embargo, es un monomorfismo en esta categoría. Esto se sigue de la implicación q ∘ h = 0 ⇒ h = 0 , que ahora probaremos. Si h : G → Q , donde G es un grupo divisible, y q ∘ h = 0 , entonces h ( x ) ∈ Z , ∀ x ∈ G . Ahora fijamos un x ∈ G . Sin pérdida de generalidad, podemos suponer que h ( x ) ≥ 0 (de lo contrario, elegimos − x en su lugar). Entonces, dejando n = h ( x ) + 1 , ya que G es un grupo divisible, existe un y ∈ G tal que x = ny , por lo que h ( x ) = n h ( y ) . De esto, y 0 ≤ h ( x ) < h ( x ) + 1 = n , se sigue que
Como h ( y ) ∈ Z , se deduce que h ( y ) = 0 , y por lo tanto h ( x ) = 0 = h (− x ), ∀ x ∈ G . Esto dice que h = 0 , como se deseaba.
Para pasar de esa implicación al hecho de que q es un monomorfismo, supongamos que q ∘ f = q ∘ g para algunos morfismos f , g : G → Q , donde G es algún grupo divisible. Entonces q ∘ ( f − g ) = 0 , donde ( f − g ) : x ↦ f ( x ) − g ( x ) . (Dado que ( f − g )(0) = 0 , y ( f − g )( x + y ) = ( f − g )( x ) + ( f − g )( y ) , se sigue que ( f − g ) ∈ Hom( G , Q ) ). De la implicación que acabamos de demostrar, q ∘ ( f − g ) = 0 ⇒ f − g = 0 ⇔ ∀ x ∈ G , f ( x ) = g ( x ) ⇔ f = g . Por lo tanto, q es un monomorfismo, como se afirma.
También existen conceptos útiles de monomorfismo regular , monomorfismo extremal , monomorfismo inmediato , monomorfismo fuerte y monomorfismo dividido .
Los términos monomorfismo y epimorfismo fueron introducidos originalmente por Nicolas Bourbaki ; Bourbaki utiliza el monomorfismo como abreviatura de una función inyectiva. Los primeros teóricos de categorías creían que la generalización correcta de la inyectividad al contexto de categorías era la propiedad de cancelación dada anteriormente. Si bien esto no es exactamente cierto para los mapas mónicos, es muy cercano, por lo que esto ha causado pocos problemas, a diferencia del caso de los epimorfismos. Saunders Mac Lane intentó hacer una distinción entre lo que llamó monomorfismos , que eran mapas en una categoría concreta cuyos mapas subyacentes de conjuntos eran inyectivos, y mapas mónicos , que son monomorfismos en el sentido categórico de la palabra. Esta distinción nunca llegó a usarse de manera general.
Otro nombre para el monomorfismo es extensión , aunque también tiene otros usos.