Simetría molecular

Simetría de moléculas de compuestos químicos.

Elementos de simetría del formaldehído . C ₂ es un eje de rotación doble. σ _v y σ _v ' son dos planos de reflexión no equivalentes.

En química , la simetría molecular describe la simetría presente en las moléculas y la clasificación de estas moléculas según su simetría. La simetría molecular es un concepto fundamental en química, ya que puede utilizarse para predecir o explicar muchas de las propiedades químicas de una molécula , como por ejemplo si tiene o no un momento dipolar , así como sus transiciones espectroscópicas permitidas . Para ello es necesario utilizar la teoría de grupos . Esto implica clasificar los estados de la molécula utilizando las representaciones irreducibles de la tabla de caracteres del grupo de simetría de la molécula. La simetría es útil en el estudio de los orbitales moleculares , con aplicaciones al método de Hückel , a la teoría del campo de ligandos y a las reglas de Woodward-Hoffmann . Muchos libros de texto de nivel universitario sobre química física , química cuántica , espectroscopia y química inorgánica tratan la simetría. ^{[1] [2] [3] [4] [5]} Otro marco a mayor escala es el uso de sistemas cristalinos para describir la simetría cristalográfica en materiales a granel.

Existen muchas técnicas para determinar la simetría de una molécula determinada, entre ellas la cristalografía de rayos X y diversas formas de espectroscopia . La notación espectroscópica se basa en consideraciones de simetría.

Conceptos de simetría de grupos puntuales

Elementos

La simetría del grupo puntual de una molécula se define por la presencia o ausencia de 5 tipos de elementos de simetría .

• Eje de simetría : eje alrededor del cual una rotación da como resultado una molécula indistinguible de la original. Esto también se denomina eje de rotación n- fold y se abrevia C _n . Algunos ejemplos son el eje C ₂ en el agua y el eje C ₃ en el amoniaco . Una molécula puede tener más de un eje de simetría; el que tiene el n más alto se denomina eje principal y, por convención, se alinea con el eje z en un sistema de coordenadas cartesianas . ${\displaystyle {\tfrac {360^{\circ }}{n}}}$
• Plano de simetría : plano de reflexión a través del cual se genera una copia idéntica de la molécula original. También se denomina plano especular y se abrevia σ (sigma = "s" del griego, del alemán "Spiegel" que significa espejo). ^[6] El agua tiene dos de ellos: uno en el plano de la propia molécula y otro perpendicular a ella. Un plano de simetría paralelo al eje principal se denomina vertical (σ _v ) y uno perpendicular a él horizontal (σ _h ). Existe un tercer tipo de plano de simetría: si un plano de simetría vertical biseca además el ángulo entre dos ejes de rotación doble perpendiculares al eje principal, el plano se denomina diedro (σ _d ). Un plano de simetría también se puede identificar por su orientación cartesiana, por ejemplo, (xz) o (yz).
• Centro de simetría o centro de inversión , abreviado i . Una molécula tiene un centro de simetría cuando, para cualquier átomo de la molécula, existe un átomo idéntico diametralmente opuesto a este centro a una distancia igual de él. En otras palabras, una molécula tiene un centro de simetría cuando los puntos (x, y, z) y (−x, −y, −z) de la molécula siempre parecen idénticos. Por ejemplo, siempre que haya un átomo de oxígeno en algún punto (x, y, z), entonces también tiene que haber un átomo de oxígeno en el punto (−x, −y, −z). Puede haber o no un átomo en el propio centro de inversión. Un centro de inversión es un caso especial de tener un eje de rotación-reflexión alrededor de un ángulo de 180° a través del centro. Los ejemplos son el tetrafluoruro de xenón (una molécula plana cuadrada), donde el centro de inversión está en el átomo de Xe, y el benceno ( C
  ₆yo
  ₆) donde el centro de inversión está en el centro del anillo.
• Eje de rotación-reflexión : eje alrededor del cual una rotación de , seguida de una reflexión en un plano perpendicular a él, deja la molécula sin cambios. También llamado eje de rotación impropio de n pliegues , se abrevia S _n . Hay ejemplos en el tetrafluoruro de silicio tetraédrico , con tres ejes S ₄ , y la conformación escalonada del etano con un eje S ₆ . Un eje S ₁ corresponde a un plano de espejo σ y un eje S ₂ es un centro de inversión i . Una molécula que no tiene eje S _n para ningún valor de n es una molécula quiral . ${\displaystyle {\tfrac {360^{\circ }}{n}}}$
• Identidad , abreviado como E , del alemán 'Einheit' que significa unidad. ^[7] Este elemento de simetría consiste simplemente en que no hay cambio: cada molécula tiene este elemento de simetría, que es equivalente a una rotación propia de C ₁ . Debe incluirse en la lista de elementos de simetría para que formen un grupo matemático , cuya definición requiere la inclusión del elemento identidad. Se llama así porque es análogo a multiplicar por uno (unidad). ^[8]

Grupos de puntos y sus operaciones de simetría

Operaciones

XeF ₄ , con geometría plana cuadrada, tiene 1 eje C ₄ y 4 ejes C _{2 ortogonales a} C ₄ . Estos cinco ejes más el plano especular perpendicular al eje C ₄ definen el grupo de simetría D _4h de la molécula.

Los cinco elementos de simetría tienen asociados cinco tipos de operaciones de simetría , que hacen que la geometría de la molécula sea indistinguible de la geometría inicial. A veces se distinguen de los elementos de simetría mediante un acento circunflejo . Por lo tanto, Ĉ _n es la rotación de una molécula alrededor de un eje y Ê es la operación de identidad. Un elemento de simetría puede tener más de una operación de simetría asociada. Por ejemplo, el eje C _{4 de la molécula} de tetrafluoruro de xenón cuadrado (XeF ₄ ) está asociado con dos rotaciones Ĉ ₄ en direcciones opuestas (90° y 270°), una rotación Ĉ ₂ (180°) y Ĉ ₁ (0° o 360°). Debido a que Ĉ ₁ es equivalente a Ê , Ŝ ₁ a σ y Ŝ ₂ a î , todas las operaciones de simetría se pueden clasificar como rotaciones propias o impropias.

Para las moléculas lineales, la rotación en el sentido de las agujas del reloj o en el sentido contrario de las agujas del reloj alrededor del eje molecular en cualquier ángulo Φ es una operación de simetría.

Operaciones de rotación-reflexión para simetría octaédrica

Rotación incorrecta S ₄

Grupos de simetría

Grupos

Las operaciones de simetría de una molécula (u otro objeto) forman un grupo . En matemáticas, un grupo es un conjunto con una operación binaria que satisface las cuatro propiedades que se enumeran a continuación.

En un grupo de simetría , los elementos del grupo son las operaciones de simetría (no los elementos de simetría), y la combinación binaria consiste en aplicar primero una operación de simetría y luego la otra. Un ejemplo es la secuencia de una rotación C ₄ alrededor del eje z y una reflexión en el plano xy, denotada σ(xy) C ₄ . Por convención, el orden de las operaciones es de derecha a izquierda.

Un grupo de simetría obedece las propiedades definitorias de cualquier grupo.

1. propiedad de cierre :
   Para cada par de elementos x e y en G , el producto x * y también está en G .
   (en símbolos, para cada dos elementos x , y ∈ G , x * y también está en G ).
   Esto significa que el grupo está cerrado , de modo que la combinación de dos elementos no produce nuevos elementos. Las operaciones de simetría tienen esta propiedad porque una secuencia de dos operaciones producirá un tercer estado indistinguible del segundo y, por lo tanto, del primero, de modo que el efecto neto sobre la molécula sigue siendo una operación de simetría. Esto se puede ilustrar mediante una tabla. Por ejemplo, con el grupo puntual C ₃ , hay tres operaciones de simetría: rotación de 120°, C ₃ , rotación de 240°, C ₃ ² y rotación de 360°, que es equivalente a la identidad, E .

   

   Pestaña de multiplicación de grupos de puntos C2v

2. Esta tabla también ilustra las siguientes propiedades
3. Propiedad asociativa :
   Para cada x e y y z en G , tanto ( x * y )* z como x * ( y * z ) resultan con el mismo elemento en G .
   ( en símbolos, ( x * y )* z = x *( y * z ) para cada x , y y z ∈ G )
4. existencia de propiedad de identidad :
   Debe haber un elemento (digamos e ) en G tal que el producto de cualquier elemento de G con e no produzca ningún cambio en el elemento.
   (en símbolos, x * e = e * x = x para cada x ∈ G )
5. existencia de elemento inverso :
   Para cada elemento x en G , debe haber un elemento y en G tal que el producto de x e y sea el elemento identidad e .
   (en símbolos, para cada x ∈ G existe un y ∈ G tal que x * y = y * x = e para cada x ∈ G )

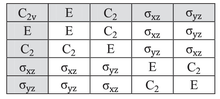
El orden de un grupo es el número de elementos que lo componen. En el caso de grupos de órdenes pequeños, las propiedades del grupo se pueden verificar fácilmente considerando su tabla de composición, una tabla cuyas filas y columnas corresponden a los elementos del grupo y cuyas entradas corresponden a sus productos.

Grupos de puntos

Diagrama de flujo para determinar el grupo puntual de una molécula

La aplicación sucesiva (o composición ) de una o más operaciones de simetría de una molécula tiene un efecto equivalente al de alguna operación de simetría individual de la molécula. Por ejemplo, una rotación de C ₂ seguida de una reflexión σ _v se considera una operación de simetría σ _v ' : σ _v * C ₂ = σ _v '. ("Operación A seguida de B para formar C " se escribe BA = C ). ^[8] Además, el conjunto de todas las operaciones de simetría (incluida esta operación de composición) obedece a todas las propiedades de un grupo, dadas anteriormente. Por lo tanto, ( S , * ) es un grupo, donde S es el conjunto de todas las operaciones de simetría de alguna molécula y * denota la composición (aplicación repetida) de las operaciones de simetría.

Este grupo se denomina grupo puntual de esa molécula, porque el conjunto de operaciones de simetría deja fijo al menos un punto (aunque para algunas simetrías un eje entero o un plano entero permanece fijo). En otras palabras, un grupo puntual es un grupo que resume todas las operaciones de simetría que tienen todas las moléculas de esa categoría. ^[8] La simetría de un cristal, por el contrario, se describe mediante un grupo espacial de operaciones de simetría, que incluye las traslaciones en el espacio.

Ejemplos de grupos de puntos

Asignar a cada molécula un grupo puntual clasifica las moléculas en categorías con propiedades de simetría similares. Por ejemplo, PCl ₃ , POF ₃ , XeO ₃ y NH ₃ comparten operaciones de simetría idénticas. ^[9] Todas pueden experimentar la operación de identidad E , dos operaciones de rotación de C ₃ diferentes y tres reflexiones planas σ _v diferentes sin alterar sus identidades, por lo que se colocan en un grupo puntual, C _3v , con orden 6. ^[8] De manera similar, el agua (H ₂ O) y el sulfuro de hidrógeno (H ₂ S) también comparten operaciones de simetría idénticas. Ambas experimentan la operación de identidad E , una rotación de C ₂ y dos reflexiones σ _v sin alterar sus identidades, por lo que ambas se colocan en un grupo puntual, C _2v , con orden 4. ^[10] Este sistema de clasificación ayuda a los científicos a estudiar las moléculas de manera más eficiente, ya que las moléculas químicamente relacionadas en el mismo grupo puntual tienden a exhibir esquemas de enlace, diagramas de enlace molecular y propiedades espectroscópicas similares. ^[8] La simetría de grupo puntual describe la simetría de una molécula cuando se encuentra fija en su configuración de equilibrio en un estado electrónico particular. No permite la tunelización entre mínimos ni el cambio de forma que puede producirse por los efectos de distorsión centrífuga de la rotación molecular.

Grupos de puntos comunes

En la siguiente tabla se enumeran muchos de los grupos de puntos aplicables a las moléculas, etiquetados con la notación de Schoenflies , que es común en química y espectroscopia molecular. Las descripciones incluyen formas comunes de moléculas, que pueden explicarse mediante el modelo RPECV . En cada fila, las descripciones y los ejemplos no tienen simetrías superiores, lo que significa que el grupo de puntos nombrado captura todas las simetrías de puntos.

Representaciones

Un conjunto de matrices que se multiplican entre sí de una manera que imita la tabla de multiplicación de los elementos de un grupo se denomina representación del grupo. Por ejemplo, para el grupo puntual C _2v , las tres matrices siguientes forman parte de una representación del grupo:

${\displaystyle \underbrace {\begin{bmatrix}-1&0&0\\0&-1&0\\0&0&1\\\end{bmatrix}} _{C_{2}}\times \underbrace {\begin{bmatrix}1&0&0\\0&-1&0\\0&0&1\\\end{bmatrix}} _{\sigma _{\text{v}}}=\underbrace {\begin{bmatrix}-1&0&0\\0&1&0\\0&0&1\\\end{bmatrix}} _{\sigma '_{\text{v}}}}$

Aunque existe un número infinito de representaciones de este tipo, las representaciones irreducibles (o "irreps") del grupo son todo lo que se necesita, ya que todas las demás representaciones del grupo pueden describirse como una suma directa de las representaciones irreducibles. Además, las representaciones irreducibles son aquellas representaciones matriciales en las que las matrices están en su forma más diagonal posible.

Operaciones de simetría de matrices de transformación

Tablas de caracteres

Para cualquier grupo, su tabla de caracteres da una tabulación (para las clases del grupo) de los caracteres (la suma de los elementos diagonales) de las matrices de todas las representaciones irreducibles del grupo. Como el número de representaciones irreducibles es igual al número de clases, la tabla de caracteres es cuadrada.

Las representaciones se etiquetan según un conjunto de convenciones:

• A, cuando la rotación alrededor del eje principal es simétrica
• B, cuando la rotación alrededor del eje principal es asimétrica
• E y T son representaciones doble y triplemente degeneradas , respectivamente.
• cuando el grupo de puntos tiene un centro de inversión, el subíndice g ( en alemán : gerade o par) no indica cambio de signo, y el subíndice u ( ungerade o desigual) un cambio de signo, con respecto a la inversión.
• con grupos de puntos C _∞v y D _∞h los símbolos se toman prestados de la descripción del momento angular : Σ , Π , Δ .

Las tablas también recogen información sobre cómo los vectores base cartesianos, las rotaciones sobre ellos y las funciones cuadráticas de ellos se transforman mediante las operaciones de simetría del grupo, señalando qué representación irreducible se transforma de la misma manera. Estas indicaciones se encuentran convencionalmente en el lado derecho de las tablas. Esta información es útil porque los orbitales químicamente importantes (en particular los orbitales p y d ) tienen las mismas simetrías que estas entidades.

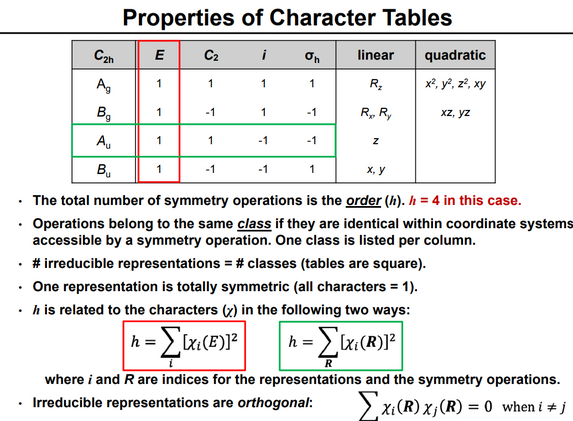
La tabla de caracteres para el grupo de puntos de simetría C _2v se muestra a continuación:

Consideremos el ejemplo del agua (H ₂ O), que tiene la simetría C _2v descrita anteriormente. El orbital 2 p _x del oxígeno tiene simetría B ₁ como en la cuarta fila de la tabla de caracteres anterior, con x en la sexta columna). Está orientado perpendicularmente al plano de la molécula y cambia de signo con una operación C ₂ y σ _v '(yz), pero permanece inalterado con las otras dos operaciones (obviamente, el carácter para la operación de identidad es siempre +1). El conjunto de caracteres de este orbital es, por tanto, {1, −1, 1, −1}, correspondiente a la representación irreducible B _1. Del mismo modo, se observa que el orbital 2 p _z tiene la simetría de la representación irreducible A _{1 (} es decir , ninguna de las operaciones de simetría lo cambia), 2 p _y B ₂ y el orbital 3 d _{xy A 2.} Estas asignaciones y otras se indican en las dos columnas más a la derecha de la tabla.

Propiedades de la tabla de caracteres

Antecedentes históricos

Hans Bethe utilizó caracteres de operaciones de grupos puntuales en su estudio de la teoría de campos de ligandos en 1929, y Eugene Wigner utilizó la teoría de grupos para explicar las reglas de selección de la espectroscopia atómica . ^[13] Las primeras tablas de caracteres fueron compiladas por László Tisza (1933), en relación con los espectros vibracionales. Robert Mulliken fue el primero en publicar tablas de caracteres en inglés (1933), y E. Bright Wilson las utilizó en 1934 para predecir la simetría de los modos normales vibracionales . ^[14] Todas las operaciones de grupo descritas anteriormente y los símbolos para los grupos puntuales cristalográficos en sí fueron publicados por primera vez por Arthur Schoenflies en 1891, pero los grupos habían sido aplicados por otros investigadores a la morfología externa de los cristales mucho antes en el siglo XIX. El conjunto completo de 32 grupos puntuales cristalográficos fue publicado en 1936 por Rosenthal y Murphy ^[15]

Algunas aplicaciones de la simetría molecular

Se pueden determinar las operaciones de simetría del grupo puntual para una molécula particular considerando la simetría geométrica de su modelo molecular. Sin embargo, cuando se utiliza un grupo puntual para clasificar estados moleculares, las operaciones en él no se deben interpretar de la misma manera. En cambio, las operaciones se interpretan como rotaciones y/o reflejos de las coordenadas vibrónicas (vibración-electrónicas) y estas operaciones conmutan con el hamiltoniano vibrónico. ^[16] Son "operaciones de simetría" para ese hamiltoniano vibrónico. El grupo puntual se utiliza para clasificar por simetría los estados propios vibrónicos de una molécula rígida. La clasificación por simetría de los niveles rotacionales, los estados propios del hamiltoniano completo (rotación-vibración-electrónica), se puede lograr mediante el uso del grupo de permutación-inversión apropiado, como lo introdujo Longuet-Higgins . ^[17]

Simetría de los modos vibracionales

Cada modo normal de vibración molecular tiene una simetría que forma una base para una representación irreducible del grupo de simetría molecular. ^[18] Por ejemplo, la molécula de agua tiene tres modos normales de vibración: estiramiento simétrico en el que las dos longitudes de enlace OH varían en fase entre sí, estiramiento asimétrico en el que varían fuera de fase y flexión en el que varía el ángulo de enlace. La simetría molecular del agua es C _2v con cuatro representaciones irreducibles A ₁ , A ₂ , B ₁ y B ₂ . Los modos de estiramiento simétrico y flexión tienen simetría A ₁ , mientras que el modo asimétrico tiene simetría B ₂ . La simetría general de los tres modos vibracionales es, por lo tanto, Γ _vib = 2A ₁ + B ₂ . ^{[18] [19]}

Modos vibracionales del amoniaco

La simetría molecular del amoniaco (NH ₃ ) es C _3v , con operaciones de simetría E, C ₃ y σ _v . ^[6] Para N = 4 átomos, el número de modos vibracionales para una molécula no lineal es 3N-6 = 6, debido al movimiento relativo del átomo de nitrógeno y los tres átomos de hidrógeno. Los tres átomos de hidrógeno viajan simétricamente a lo largo de los enlaces NH, ya sea en la dirección del átomo de nitrógeno o alejándose de él. Este modo se conoce como estiramiento simétrico (v₁) y refleja la simetría en el estiramiento del enlace NH. De los tres modos vibracionales, este tiene la frecuencia más alta . ^[20]

Molécula de amoniaco ^[21]

En la vibración de flexión (ν₂), el átomo de nitrógeno permanece en el eje de simetría, mientras que los tres átomos de hidrógeno se mueven en direcciones diferentes entre sí, lo que provoca cambios en los ángulos de enlace. Los átomos de hidrógeno se mueven como un paraguas, por lo que este modo se conoce a menudo como "modo paraguas". ^[22]

También existe un modo de estiramiento asimétrico (ν₃) en el que un átomo de hidrógeno se aproxima al átomo de nitrógeno mientras que los otros dos hidrógenos se alejan.

Se puede determinar el número total de grados de libertad para cada especie de simetría (o representación irreducible ). El amoniaco tiene cuatro átomos y cada átomo está asociado con tres componentes vectoriales . El grupo de simetría C _3v para NH ₃ tiene las tres especies de simetría A ₁ , A ₂ y E. Los modos de vibración incluyen los modos vibracional, rotacional y traslacional.

Modos totales = 3A ₁ + A ₂ + 4E. Esto es un total de 12 modos porque cada E corresponde a 2 modos degenerados (con la misma energía).

Modos rotacionales = A2 ₊ E (3 modos)

Modos de traducción = A ₁ + E

Modos vibracionales = Modos totales - Modos rotacionales - Modos traslacionales = 3A ₁ + A ₂ + 4E - A ₂ - E - A ₁ - E = 2A ₁ + 2E (6 modos).

Más ejemplos de simetría vibracional

• W(CO) ₆ tiene geometría octaédrica . La representación irreducible de la vibración de estiramiento del CO es A _1g + E _g + T _1u . De estas, solo T _1u es activo en IR.
• El B ₂ H ₆ ( diborano ) tiene simetría molecular D _2h . Las vibraciones de estiramiento BH terminales que están activas en IR son B _2u y B _3u .

Diborano

• Fac -Mo(CO) ₃ (CH ₃ CH ₂ CN) ₃ , tiene geometría C _3v . La representación irreducible para la vibración de estiramiento de CO es A ₁ + E. Ambos son activos en IR.

Simetría de los orbitales moleculares

Cada orbital molecular también tiene la simetría de una representación irreducible. Por ejemplo, el etileno (C ₂ H ₄ ) tiene un grupo de simetría D _2h , y su orbital molecular más alto ocupado ( HOMO ) es el orbital de enlace pi que forma una base para su representación irreducible B _1u . ^[23]

Rotación molecular y no rigidez molecular

Como se discutió anteriormente en la sección Algunas aplicaciones de la simetría molecular, los grupos puntuales son útiles para clasificar los estados vibracionales y electrónicos de moléculas rígidas (a veces llamadas moléculas semirrígidas ) que experimentan solo pequeñas oscilaciones alrededor de una única geometría de equilibrio. Longuet-Higgins introdujo un tipo más general de grupo de simetría ^[17] adecuado no solo para clasificar los estados vibracionales y electrónicos de moléculas rígidas sino también para clasificar sus estados rotacionales y de espín nuclear. Además, dichos grupos se pueden utilizar para clasificar los estados de moléculas no rígidas (o fluxionales ) que hacen túnel entre geometrías equivalentes ^[24] y para permitir los efectos distorsionadores de la rotación molecular. Estos grupos se conocen como grupos de permutación-inversión , porque las operaciones de simetría en ellos son permutaciones energéticamente factibles de núcleos idénticos, o inversión con respecto al centro de masa (la operación de paridad ), o una combinación de las dos. ^{[17] [25]}

Abundan los ejemplos de falta de rigidez molecular. Por ejemplo, el etano (C ₂ H _{6 ) tiene tres} conformaciones escalonadas equivalentes . El efecto túnel entre las conformaciones se produce a temperaturas ordinarias por rotación interna de un grupo metilo con respecto al otro. No se trata de una rotación de la molécula entera sobre el eje C _{3 , aunque cada conformación tiene simetría} D _3d , como en la tabla anterior. De manera similar, el amoníaco (NH ₃ ) tiene dos conformaciones piramidales equivalentes ( C _3v ) que se interconvierten mediante el proceso conocido como inversión de nitrógeno .

Además, las moléculas de metano (CH ₄ ) y H ₃ ⁺ tienen estructuras de equilibrio altamente simétricas con simetrías de grupo puntual T _d y D _3h respectivamente; carecen de momentos dipolares eléctricos permanentes pero tienen espectros de rotación pura muy débiles debido a la distorsión centrífuga rotacional. ^{[26] [27]}

A veces es necesario considerar juntos estados electrónicos que tienen diferentes simetrías de grupo puntual en equilibrio. Por ejemplo, en su estado electrónico fundamental (N), la molécula de etileno C ₂ H ₄ tiene simetría de grupo puntual D _2h, mientras que en el estado excitado (V) tiene simetría D _2d . Para tratar estos dos estados juntos es necesario permitir la torsión y utilizar el grupo doble del grupo de permutación-inversión G ₁₆ . ^[28]

Véase también

• Paridad (física) § Moléculas
• Representación irreducible § Aplicaciones en física teórica y química
• Reglas de Woodward-Hoffmann § Diagramas de correlación
• Hapticidad § Hapticidad y fluxionalidad
• Tabla de caracteres
• Grupo puntual cristalográfico
• Grupos de puntos en tres dimensiones
• Simetría de moléculas diatómicas
• Simetría en mecánica cuántica

Referencias

1. Química cuántica , 3.ª ed. John P. Lowe, Kirk Peterson ISBN  0-12-457551-X
2. Química física: un enfoque molecular por Donald A. McQuarrie, John D. Simon ISBN 0-935702-99-7 
3. El enlace químico , 2ª ed. JN Murrell, SFA Kettle, JM Tedder ISBN 0-471-90760-X 
4. Química física , 8.ª ed. P. W. Atkins y J. de Paula, WH Freeman, 2006 ISBN 0-7167-8759-8 , cap. 12 
5. GL Miessler y DA Tarr Química inorgánica , 2.ª ed. Pearson, Prentice Hall, 1998 ISBN 0-13-841891-8 , cap. 4. 
6. "Operaciones de simetría y tablas de caracteres". Universidad de Exeter . 2001 . Consultado el 29 de mayo de 2018 .
7. LEO Ergebnisse para "einheit"
8. Pfenning, Brian (2015). Principios de química inorgánica . John Wiley & Sons. ISBN 9781118859025.
9. Pfennig, Brian (30 de marzo de 2015). Principios de química inorgánica . Wiley. pág. 191. ISBN 978-1-118-85910-0.
10. Miessler, Gary (2004). Química inorgánica . Pearson. ISBN 9780321811059.
11. Miessler, Gary L.; Tarr, Donald A. (1999). "Tablas de caracteres (todas excepto D7h)". Química inorgánica (2.ª ed.). Prentice-Hall. págs. 621–630. ISBN 0-13-841891-8.
12. Housecroft, CE; Sharpe, AG (2008). Química inorgánica (3.ª ed.). Prentice Hall. págs. 111-112. ISBN 978-0-13-175553-6.
13. Teoría de grupos y su aplicación a la mecánica cuántica de los espectros atómicos , EP Wigner, Academic Press Inc. (1959)
14. Corrección de dos errores de larga data en las tablas de caracteres de simetría de grupos de puntos Randall B. Shirts J. Chem. Educ. 2007, 84, 1882. Resumen
15. Rosenthal, Jenny E.; Murphy, GM (1936). "Teoría de grupos y vibraciones de moléculas poliatómicas". Rev. Mod. Phys . 8 (4): 317–346. Bibcode :1936RvMP....8..317R. doi :10.1103/RevModPhys.8.317.
16. Hougen, Jon T. (1962). "Clasificación de los niveles de energía rotacional para moléculas simétricas superiores". J Chem Phys . 37 (7): 1433. doi :10.1063/1.1733301.
17. Longuet-Higgins, HC (1963). "Los grupos de simetría de moléculas no rígidas". Física molecular . 6 (5): 445–460. Bibcode :1963MolPh...6..445L. doi : 10.1080/00268976300100501 .
18. Harris, Daniel C.; Bertolucci, Michael D. (1978). "3". Simetría y espectroscopia . Oxford University Press. págs. 138-142. ISBN 0-19-502001-4Cada modo normal de vibración formará un conjunto base para una representación irreducible del grupo puntual de la molécula.
19. GL Miessler y DA Tarr Química inorgánica , 2.ª ed. Pearson, Prentice Hall, 1998 ISBN 0-13-841891-8 , págs. 97-100. 
20. "Modos vibracionales del amoniaco". www.chem.purdue.edu . Consultado el 13 de abril de 2024 .
21. Greenwood, NN; Earnshaw, A. (1997)   Química de los elementos (2.ª ed.), Oxford: Butterworth-Heinemann, págs. 423   ISBN 0-7506-3365-4 
22. "Modo paraguas - Gran enciclopedia química". chempedia.info . Consultado el 13 de abril de 2024 .
23. Harris, Daniel C.; Bertolucci, Michael D. (1978). "4". Simetría y espectroscopia . Oxford University Press. pág. 278. ISBN 0-19-502001-4.
24. Bone, RGA; et al. (1991). "Estados de transición de grupos de simetría molecular: análisis de trímeros de acetileno no rígidos". Física molecular . 72 (1): 33–73. Código Bibliográfico :1991MolPh..72...33B. doi :10.1080/00268979100100021.
25. Schnell, M. (2010). "Comprensión de los espectros de alta resolución de moléculas no rígidas mediante la teoría de grupos". ChemPhysChem . 11 (4): 750–780. doi :10.1002/cphc.200900760.
26. Watson, JKG (1971). "Espectros rotacionales prohibidos de moléculas poliatómicas". Journal of Molecular Spectroscopy . 40 (3): 546–544. Código Bibliográfico :1971JMoSp..40..536W. doi :10.1016/0022-2852(71)90255-4.
27. Oldani, M.; et al. (1985). "Espectros rotacionales puros de metano y metano-d4 en el estado fundamental vibracional observados mediante espectroscopia de transformada de Fourier de microondas". Journal of Molecular Spectroscopy . 110 (1): 93–105. Bibcode :1985JMoSp.110...93O. doi :10.1016/0022-2852(85)90215-2.
28. Watson, JKG; et al. (1996). "Teoría de transiciones torsionales impares en el espectro de resonancia Raman V−N del etileno". J Chem Phys . 105 (4): 1348. Bibcode :1996JChPh.105.1348W. doi : 10.1063/1.472001 .

Enlaces externos

• El grupo de simetría molecular[1] @ La Universidad de Western Ontario
• Simetría de grupos puntuales en la Universidad de Newcastle
• Simetría molecular en el Imperial College de Londres
• Tablas de simetría de grupos puntuales moleculares
• Tablas de caracteres para grupos de puntos de química
• Simetría molecular en línea en la Universidad Abierta de Israel

• Un curso en Internet sobre simetría molecular @ Bergische Universitaet
• DECOR – Simetría en el Centro de Datos Cristalográficos de Cambridge