Modelos compartimentales en epidemiología.

Tipo de modelo matemático utilizado para enfermedades infecciosas.

Los modelos compartimentales son una técnica de modelado muy general. A menudo se aplican a la modelización matemática de enfermedades infecciosas . La población se asigna a compartimentos con etiquetas, por ejemplo, S , I o R ( susceptible , infeccioso o recuperado ). Las personas pueden progresar entre compartimentos. El orden de las etiquetas suele mostrar los patrones de flujo entre los compartimentos; por ejemplo, SEIS significa susceptible, expuesto, infeccioso y luego susceptible nuevamente.

El origen de este tipo de modelos es de principios del siglo XX, siendo obras importantes la de Ross ^[1] en 1916, Ross y Hudson en 1917, ^{[2] [3]} Kermack y McKendrick en 1927, ^[4] y Kendall en 1956. ^[5] El modelo Reed-Frost también fue un ancestro importante y ampliamente pasado por alto de los enfoques modernos de modelización epidemiológica. ^[6]

Los modelos suelen ejecutarse con ecuaciones diferenciales ordinarias (que son deterministas), pero también se pueden utilizar con un marco estocástico (aleatorio), que es más realista pero mucho más complicado de analizar.

Los modelos intentan predecir cosas como cómo se propaga una enfermedad, el número total de infectados o la duración de una epidemia, y estimar diversos parámetros epidemiológicos, como el número reproductivo . Dichos modelos pueden mostrar cómo diferentes intervenciones de salud pública pueden afectar el resultado de la epidemia, por ejemplo, cuál es la técnica más eficiente para administrar un número limitado de vacunas en una población determinada.

El modelo SIR

El modelo SIR ^{[7] [8] [9] [10]} es uno de los modelos compartimentales más simples y muchos modelos son derivados de esta forma básica. El modelo consta de tres compartimentos:

S : El número de individuos susceptibles. Cuando un individuo susceptible y un individuo infeccioso entran en "contacto infeccioso", el individuo susceptible contrae la enfermedad y pasa al compartimento infeccioso.

I : El número de individuos infecciosos . Se trata de individuos que han sido infectados y son capaces de infectar a individuos susceptibles.

R para el número de personas eliminadas (e inmunes) o fallecidas. Se trata de personas que han sido infectadas y se han recuperado de la enfermedad y han entrado en el compartimento eliminado o han muerto. Se supone que el número de muertes es insignificante con respecto a la población total. Este compartimento también puede denominarse " recuperado " o " resistente ".

Este modelo es razonablemente predictivo ^[11] para enfermedades infecciosas que se transmiten de persona a persona y donde la recuperación confiere una resistencia duradera, como el sarampión , las paperas y la rubéola .

Simulación del modelo SIR espacial. Cada célula puede infectar a sus ocho vecinos inmediatos.

Estas variables ( S , I y R ) representan el número de personas en cada compartimento en un momento determinado. Para representar que el número de individuos susceptibles, infecciosos y eliminados puede variar con el tiempo (incluso si el tamaño total de la población permanece constante), hacemos que los números precisos sean función de t (tiempo): S ( t ), I ( t ) y R ( t ). Para una enfermedad específica en una población específica, estas funciones pueden desarrollarse para predecir posibles brotes y controlarlos. ^[11]

Como lo implica la función variable de t , el modelo es dinámico en el sentido de que los números en cada compartimento pueden fluctuar con el tiempo. La importancia de este aspecto dinámico es más obvia en una enfermedad endémica con un período infeccioso corto, como el sarampión en el Reino Unido antes de la introducción de una vacuna en 1968. Estas enfermedades tienden a ocurrir en ciclos de brotes debido a la variación en el número de susceptibles (S( t )) a lo largo del tiempo. Durante una epidemia , el número de individuos susceptibles disminuye rápidamente a medida que un mayor número de ellos se infecta y entra así en los compartimentos infecciosos y eliminados. La enfermedad no puede reaparecer hasta que el número de susceptibles se haya vuelto a acumular, por ejemplo, como resultado del nacimiento de descendencia en el compartimento susceptible. ^{[ cita necesaria ]}

Amarillo=Susceptible, Granate=Infeccioso, Verde azulado=Recuperado

Cada miembro de la población generalmente pasa de ser susceptible a infeccioso a recuperarse. Esto se puede mostrar como un diagrama de flujo en el que los cuadros representan los diferentes compartimentos y las flechas la transición entre compartimentos (ver diagrama).

Diagrama de flujo de estados en un modelo epidémico SIR y tasas de transición entre ellos

Tasas de transición

Para obtener la especificación completa del modelo, las flechas deben estar etiquetadas con las tasas de transición entre compartimentos. Entre S e I , se supone que la tasa de transición es , donde es la población total, es el número promedio de contactos por persona por vez, multiplicado por la probabilidad de transmisión de enfermedades en un contacto entre un sujeto susceptible y uno infeccioso, y es la fracción de esos contactos entre un individuo infeccioso y susceptible que resultan en que la persona susceptible se infecte. (Esto es matemáticamente similar a la ley de acción de masas en química en la que las colisiones aleatorias entre moléculas dan como resultado una reacción química y la velocidad fraccionaria es proporcional a la concentración de los dos reactivos. ^[12] ) ${\displaystyle d(S/N)/dt=-\beta SI/N^{2}}$ ${\displaystyle N}$ ${\displaystyle \beta }$ ${\displaystyle SI/N^{2}}$

Entre I y R , se supone que la tasa de transición es proporcional al número de individuos infecciosos que es . Si un individuo es infeccioso durante un período de tiempo promedio , entonces . Esto también equivale a suponer que el tiempo que pasa un individuo en estado infeccioso es una variable aleatoria con una distribución exponencial . El modelo SIR "clásico" puede modificarse mediante el uso de distribuciones más complejas y realistas para la tasa de transición IR (por ejemplo, la distribución de Erlang ). ^[13] ${\displaystyle \gamma I}$ ${\displaystyle D}$ ${\displaystyle \gamma =1/D}$

Para el caso especial en el que no hay eliminación del compartimento infeccioso ( ), el modelo SIR se reduce a un modelo SI muy simple, que tiene una solución logística , en la que cada individuo eventualmente se infecta. ${\displaystyle \gamma =0}$

El modelo SIR sin nacimiento ni muerte

Una realización única de la epidemia SIR producida con una implementación del algoritmo de Gillespie y la solución numérica del sistema de ecuaciones diferenciales ordinarias (discontinuo)

La dinámica de una epidemia, por ejemplo, la gripe , suele ser mucho más rápida que la dinámica del nacimiento y la muerte; por lo tanto, el nacimiento y la muerte a menudo se omiten en los modelos compartimentales simples. El sistema SIR sin la llamada dinámica vital (nacimiento y muerte, a veces llamado demografía) descrito anteriormente puede expresarse mediante el siguiente sistema de ecuaciones diferenciales ordinarias : ^{[8] [14]}

${\displaystyle \left\{{\begin{aligned}&{\frac {dS}{dt}}=-{\frac {\beta IS}{N}},\\[6pt]&{\frac {dI}{dt}}={\frac {\beta IS}{N}}-\gamma I,\\[6pt]&{\frac {dR}{dt}}=\gamma I,\end{aligned}}\right.}$

El modelo SIR

donde es el stock de población susceptible, es el stock de infectados, es el stock de población eliminada (ya sea por muerte o recuperación) y es la suma de estos tres. ${\displaystyle S}$ ${\displaystyle I}$ ${\displaystyle R}$ ${\displaystyle N}$

Este modelo fue propuesto por primera vez por William Ogilvy Kermack y Anderson Gray McKendrick como un caso especial de lo que ahora llamamos teoría de Kermack-McKendrick , y siguió al trabajo que McKendrick había realizado con Ronald Ross . ^{[ cita necesaria ]}

Este sistema no es lineal , sin embargo es posible derivar su solución analítica de forma implícita. ^[7] En primer lugar, tenga en cuenta que de:

${\displaystyle {\frac {dS}{dt}}+{\frac {dI}{dt}}+{\frac {dR}{dt}}=0,}$

resulta que:

${\displaystyle S(t)+I(t)+R(t)={\text{constant}}=N,}$

expresando en términos matemáticos la constancia de la población . Tenga en cuenta que la relación anterior implica que sólo es necesario estudiar la ecuación para dos de las tres variables. ${\displaystyle N}$

En segundo lugar, observamos que la dinámica de la clase infecciosa depende de la siguiente proporción:

${\displaystyle R_{0}={\frac {\beta }{\gamma }},}$

el llamado número de reproducción básico (también llamado índice de reproducción básico). Esta relación se deriva del número esperado de nuevas infecciones (estas nuevas infecciones a veces se denominan infecciones secundarias) de una única infección en una población en la que todos los sujetos son susceptibles. ^{[15] [16]} Esta idea probablemente pueda verse más fácilmente si decimos que el tiempo típico entre contactos es y el tiempo típico hasta la eliminación es . De aquí se deduce que, en promedio, el número de contactos de un individuo infeccioso con otros antes de que el infeccioso haya sido eliminado es: ${\displaystyle T_{c}=\beta ^{-1}}$ ${\displaystyle T_{r}=\gamma ^{-1}}$ ${\displaystyle T_{r}/T_{c}.}$

Dividiendo la primera ecuación diferencial por la tercera, separando las variables e integrando obtenemos

${\displaystyle S(t)=S(0)e^{-R_{0}(R(t)-R(0))/N},}$

donde y son los números iniciales de sujetos susceptibles y eliminados, respectivamente. Escribiendo para la proporción inicial de individuos susceptibles, y para la proporción de individuos susceptibles y eliminados respectivamente en el límite que se tiene ${\displaystyle S(0)}$ ${\displaystyle R(0)}$ ${\displaystyle s_{0}=S(0)/N}$ ${\displaystyle s_{\infty }=S(\infty )/N}$ ${\displaystyle r_{\infty }=R(\infty )/N}$ ${\displaystyle t\to \infty ,}$

${\displaystyle s_{\infty }=1-r_{\infty }=s_{0}e^{-R_{0}(r_{\infty }-r_{0})}}$

(tenga en cuenta que el compartimento infeccioso se vacía en este límite). Esta ecuación trascendental tiene una solución en términos de la función Lambert W , ^[17] a saber

${\displaystyle s_{\infty }=1-r_{\infty }=-R_{0}^{-1}\,W(-s_{0}R_{0}e^{-R_{0}(1-r_{0})}).}$

Esto muestra que al final de una epidemia que se ajusta a los supuestos simples del modelo SIR, a menos que no todos los individuos de la población hayan sido eliminados, algunos deben seguir siendo susceptibles. Una fuerza impulsora que conduce al fin de una epidemia es la disminución del número de personas infecciosas. Por lo general, la epidemia no termina debido a una falta total de personas susceptibles. ${\displaystyle s_{0}=0}$

El papel tanto del número de reproducción básico como de la susceptibilidad inicial es extremadamente importante. De hecho, al reescribir la ecuación para individuos infecciosos de la siguiente manera:

${\displaystyle {\frac {dI}{dt}}=\left(R_{0}{\frac {S}{N}}-1\right)\gamma I,}$

se obtiene que si:

${\displaystyle R_{0}\cdot S(0)>N,}$

entonces:

${\displaystyle {\frac {dI}{dt}}(0)>0,}$

es decir, habrá un verdadero brote epidémico con un aumento del número de infecciosos (que pueden alcanzar a una fracción considerable de la población). Por el contrario, si

${\displaystyle R_{0}\cdot S(0)<N,}$

entonces

${\displaystyle {\frac {dI}{dt}}(0)<0,}$

es decir, independientemente del tamaño inicial de la población susceptible, la enfermedad nunca puede causar un brote epidémico adecuado. Como consecuencia, está claro que tanto el número de reproducción básico como la susceptibilidad inicial son extremadamente importantes.

La fuerza de la infección

Tenga en cuenta que en el modelo anterior la función:

${\displaystyle F=\beta I,}$

modela la tasa de transición del compartimento de individuos susceptibles al compartimento de individuos infecciosos, por lo que se denomina fuerza de infección . Sin embargo, para grandes clases de enfermedades transmisibles es más realista considerar una fuerza de infección que no dependa del número absoluto de sujetos infecciosos, sino de su fracción (con respecto a la población constante total ): ${\displaystyle N}$

${\displaystyle F=\beta {\frac {I}{N}}.}$

Capasso ^[18] y, posteriormente, otros autores han propuesto fuerzas de infección no lineales para modelar de manera más realista el proceso de contagio.

Soluciones analíticas exactas al modelo SIR

En 2014, Harko y sus coautores derivaron la llamada solución analítica exacta (que implica una integral que solo se puede calcular numéricamente) para el modelo SIR. ^[7] En el caso sin configuración de dinámica vital, para , etc., corresponde a la siguiente parametrización de tiempo ${\displaystyle {\mathcal {S}}(u)=S(t)}$

${\displaystyle {\mathcal {S}}(u)=S(0)u}$

${\displaystyle {\mathcal {I}}(u)=N-{\mathcal {R}}(u)-{\mathcal {S}}(u)}$

${\displaystyle {\mathcal {R}}(u)=R(0)-\rho \ln(u)}$

para

${\displaystyle t={\frac {N}{\beta }}\int _{u}^{1}{\frac {du^{*}}{u^{*}{\mathcal {I}}(u^{*})}},\quad \rho ={\frac {\gamma N}{\beta }},}$

con condiciones iniciales

${\displaystyle ({\mathcal {S}}(1),{\mathcal {I}}(1),{\mathcal {R}}(1))=(S(0),N-R(0)-S(0),R(0)),\quad u_{T}<u<1,}$

donde satisface . Por la ecuación trascendental anterior , se deduce que , si y . ${\displaystyle u_{T}}$ ${\displaystyle {\mathcal {I}}(u_{T})=0}$ ${\displaystyle R_{\infty }}$ ${\displaystyle u_{T}=e^{-(R_{\infty }-R(0))/\rho }(=S_{\infty }/S(0)}$ ${\displaystyle S(0)\neq 0)}$ ${\displaystyle I_{\infty }=0}$

Una llamada solución analítica equivalente (que implica una integral que sólo puede calcularse numéricamente) encontrada por Miller ^{[19] [20]} produce

${\displaystyle {\begin{aligned}S(t)&=S(0)e^{-\xi (t)}\\[8pt]I(t)&=N-S(t)-R(t)\\[8pt]R(t)&=R(0)+\rho \xi (t)\\[8pt]\xi (t)&={\frac {\beta }{N}}\int _{0}^{t}I(t^{*})\,dt^{*}\end{aligned}}}$

Aquí se puede interpretar como el número esperado de transmisiones que un individuo ha recibido por tiempo . Las dos soluciones están relacionadas por . ${\displaystyle \xi (t)}$ ${\displaystyle t}$ ${\displaystyle e^{-\xi (t)}=u}$

Efectivamente, se puede encontrar el mismo resultado en el trabajo original de Kermack y McKendrick. ^[4]

Estas soluciones pueden entenderse fácilmente si observamos que todos los términos en el lado derecho de las ecuaciones diferenciales originales son proporcionales a . Por lo tanto, las ecuaciones pueden dividirse por y reescalarse el tiempo de modo que el operador diferencial del lado izquierdo se convierta en simplemente , donde , es decir . Ahora todas las ecuaciones diferenciales son lineales, y la tercera ecuación, de la forma const., muestra que y (y más arriba) están simplemente relacionados linealmente. ${\displaystyle I}$ ${\displaystyle I}$ ${\displaystyle d/d\tau }$ ${\displaystyle d\tau =Idt}$ ${\displaystyle \tau =\int Idt}$ ${\displaystyle dR/d\tau =}$ ${\displaystyle \tau }$ ${\displaystyle R}$ ${\displaystyle \xi }$

^{Kröger y Schlickeiser [9]} proporcionaron una aproximación analítica altamente precisa del modelo SIR, así como expresiones analíticas exactas para los valores finales , , y, de modo que no hay necesidad de realizar una integración numérica para resolver el modelo SIR (una Aquí se puede encontrar un ejemplo de práctica simplificada sobre simulación numérica de COVID-19 utilizando Microsoft Excel ^[21] ), para obtener sus parámetros a partir de datos existentes o para predecir la dinámica futura de una epidemia modelada por el modelo SIR. La aproximante implica la función Lambert W , que forma parte de todo el software básico de visualización de datos, como Microsoft Excel, MATLAB y Mathematica . ${\displaystyle S_{\infty }}$ ${\displaystyle I_{\infty }}$ ${\displaystyle R_{\infty }}$

Mientras Kendall ^[5] consideró el llamado modelo SIR de todos los tiempos donde las condiciones iniciales , y están acopladas a través de las relaciones anteriores, Kermack y McKendrick ^[4] propusieron estudiar el caso semitemporal más general, para el cual y son ambos arbitrarios. Esta última versión, denominada modelo SIR semitemporal, ^[9] hace predicciones sólo para tiempos futuros . También están disponibles una aproximación analítica y expresiones exactas para los valores finales para el modelo SIR semi-tiempo. ^[10] ${\displaystyle S(0)}$ ${\displaystyle I(0)}$ ${\displaystyle R(0)}$ ${\displaystyle S(0)}$ ${\displaystyle I(0)}$ ${\displaystyle t>0}$

Soluciones numéricas al modelo SIR con aproximaciones.

Las soluciones numéricas al modelo SIR se pueden encontrar en la literatura. Un ejemplo es el uso del modelo para analizar los datos de propagación de COVID-19 . ^{[21] [22]} Se pueden extraer tres números de reproducción de los datos analizados con aproximación numérica,

el número de reproducción básico :

${\displaystyle R_{0}={\frac {\beta _{0}}{\gamma _{0}}}}$

el número de reproducción en tiempo real:

${\displaystyle R_{t}={\frac {\beta _{t}}{\gamma _{t}}}}$

y el número de reproducción efectiva en tiempo real:

${\displaystyle R_{e}={\frac {\beta _{t}S}{\gamma _{t}N}}}$

${\displaystyle R_{0}}$representa la velocidad de la tasa de reproducción al comienzo de la propagación cuando se supone que todas las poblaciones son susceptibles, por ejemplo, si y significa que una persona infecciosa infecta en promedio a 0,4 personas susceptibles por día y se recupera en 1/0,2=5 días. Por lo tanto, cuando esta persona se recuperó, todavía hay dos personas infecciosas que se contagiaron directamente de esta persona y , es decir, el número de personas infecciosas se duplicó en un ciclo de 5 días. Los datos simulados por el modelo con datos reales ajustados producirán una duplicación del número de personas infecciosas en menos de 5 días porque las dos personas infectadas están infectando a personas. A partir del modelo SIR, podemos decir que está determinado por la naturaleza de la enfermedad y también en función de la frecuencia de interacción entre la persona infecciosa y las personas susceptibles y también por la intensidad/duración de la interacción, como qué tan cerca interactúan y durante cuánto tiempo. y si ambos usan o no máscaras, por lo tanto, cambia con el tiempo cuando cambia el comportamiento promedio de los portadores y las personas susceptibles. El modelo suele representar estos factores, pero de hecho se hace referencia a la etapa inicial cuando no se toman medidas para prevenir la propagación y toda la población es susceptible, por lo que todos los cambios son absorbidos por el cambio de . ${\displaystyle \beta _{0}=0.4day^{-1}}$ ${\displaystyle \gamma _{0}=0.2day^{-1}}$ ${\displaystyle R_{0}=2}$ ${\displaystyle R_{0}=2}$ ${\displaystyle \beta }$ ${\displaystyle I}$ ${\displaystyle S}$ ${\displaystyle SI}$ ${\displaystyle \beta }$

${\displaystyle \gamma }$suele ser más estable en el tiempo suponiendo que cuando la persona infecciosa muestre síntomas, buscará atención médica o se aislará por sí misma. Entonces, si encontramos cambios, lo más probable es que los comportamientos de las personas en la comunidad hayan cambiado de sus patrones normales antes del brote, o que la enfermedad haya mutado a una nueva forma. La costosa detección masiva y el aislamiento de contactos cercanos susceptibles tienen efectos de reducción, pero cuya eficiencia está en debate. Este debate gira en gran medida en torno a la incertidumbre del número de días reducidos desde que son infecciosos o detectables, lo que ocurra primero, hasta antes de que aparezca un síntoma en una persona infectada susceptible. Si la persona es infecciosa después de que aparecen los síntomas, o la detección solo funciona para una persona con síntomas, entonces estos métodos de prevención no son necesarios y el autoaislamiento y/o la atención médica son la mejor manera de reducir los valores. El inicio típico del período infeccioso de la COVID-19 es del orden de un día desde que aparecen los síntomas, lo que hace inútil la detección masiva con la frecuencia típica de unos pocos días. ${\displaystyle R_{t}}$ ${\displaystyle 1/\gamma }$ ${\displaystyle 1/\gamma }$

${\displaystyle R_{t}}$no nos dice si la propagación se acelerará o disminuirá en las últimas etapas, cuando la fracción de personas susceptibles en la comunidad haya disminuido significativamente después de la recuperación o la vacunación. corrige este efecto de dilución multiplicando la fracción de la población susceptible sobre la población total. Corrige la interacción efectiva/transmisible entre una persona infecciosa y el resto de la comunidad cuando muchas de las interacciones son inmunes en las etapas intermedias a tardías de la propagación de la enfermedad. Así, cuando , veremos un brote de tipo exponencial; cuando se alcanza un estado estacionario y el número de personas infecciosas no cambia con el tiempo; y cuando , la enfermedad decae y desaparece con el tiempo. ${\displaystyle R_{e}}$ ${\displaystyle R_{e}>1}$ ${\displaystyle R_{e}=1}$ ${\displaystyle R_{e}<1}$

Utilizando las ecuaciones diferenciales del modelo SIR y convirtiéndolas a formas numéricas discretas, se pueden configurar las ecuaciones recursivas y calcular las poblaciones S, I y R con cualquier condición inicial dada, pero se acumulan errores durante un largo tiempo de cálculo desde el punto de referencia. . A veces es necesaria una prueba de convergencia para estimar los errores. Dado un conjunto de condiciones iniciales y los datos de propagación de enfermedades, también se pueden ajustar los datos con el modelo SIR y extraer los tres números de reproducción cuando los errores suelen ser insignificantes debido al corto paso de tiempo desde el punto de referencia. ^{[21] [22]} Cualquier punto del tiempo puede usarse como condición inicial para predecir el futuro después usando este modelo numérico con el supuesto de parámetros evolucionados en el tiempo como población, y . Sin embargo, lejos de este punto de referencia, los errores se acumularán con el tiempo, por lo que se necesita una prueba de convergencia para encontrar un paso de tiempo óptimo para obtener resultados más precisos. ${\displaystyle R_{t}}$ ${\displaystyle \gamma }$

Entre estos tres números de reproducción, es muy útil juzgar la presión de control; por ejemplo, un valor grande significa que la enfermedad se propagará muy rápidamente y es muy difícil de controlar. es más útil para predecir tendencias futuras; por ejemplo, si sabemos que las interacciones sociales se han reducido un 50% con frecuencia con respecto a antes del brote y que las intensidades de interacción entre las personas son las mismas, entonces podemos establecer . Si el distanciamiento social y las mascarillas suman otra reducción del 50% en la eficiencia de la infección, podemos establecer ... se correlacionará perfectamente con las ondas de la propagación y cuando la propagación se acelere y cuando la propagación se desacelere, por lo que será útil para establecer una predicción sobre las tendencias a corto plazo. Además, se puede utilizar para calcular directamente el umbral de población de vacunación/inmunización para la etapa de inmunidad colectiva estableciendo . ${\displaystyle R_{0}}$ ${\displaystyle R_{t}}$ ${\displaystyle R_{t}=0.5R_{0}}$ ${\displaystyle R_{t}=0.25R_{0}}$ ${\displaystyle R_{e}}$ ${\displaystyle R_{e}>1}$ ${\displaystyle R_{e}<1}$ ${\displaystyle R_{t}=R_{0}}$

El modelo SIR con dinámica vital y población constante

Consideremos una población caracterizada por una tasa de mortalidad y una tasa de natalidad , y donde se está propagando una enfermedad transmisible. ^[8] El modelo con transmisión de acción de masas es: ${\displaystyle \mu }$ ${\displaystyle \Lambda }$

${\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=\Lambda -\mu S-{\frac {\beta IS}{N}}\\[8pt]{\frac {dI}{dt}}&={\frac {\beta IS}{N}}-\gamma I-\mu I\\[8pt]{\frac {dR}{dt}}&=\gamma I-\mu R\end{aligned}}}$

para lo cual el equilibrio libre de enfermedad (DFE) es:

${\displaystyle \left(S(t),I(t),R(t)\right)=\left({\frac {\Lambda }{\mu }},0,0\right).}$

En este caso, podemos derivar un número de reproducción básico :

${\displaystyle R_{0}={\frac {\beta }{\mu +\gamma }},}$

que tiene propiedades de umbral. De hecho, independientemente de los valores iniciales biológicamente significativos, se puede demostrar que:

${\displaystyle R_{0}\leq 1\Rightarrow \lim _{t\to \infty }(S(t),I(t),R(t))={\textrm {DFE}}=\left({\frac {\Lambda }{\mu }},0,0\right)}$

${\displaystyle R_{0}>1,I(0)>0\Rightarrow \lim _{t\to \infty }(S(t),I(t),R(t))={\textrm {EE}}=\left({\frac {\gamma +\mu }{\beta }},{\frac {\mu }{\beta }}\left(R_{0}-1\right),{\frac {\gamma }{\beta }}\left(R_{0}-1\right)\right).}$

El punto EE se denomina Equilibrio Endémico (la enfermedad no está totalmente erradicada y permanece en la población). Con argumentos heurísticos, se puede demostrar que puede leerse como el número promedio de infecciones causadas por un solo sujeto infeccioso en una población totalmente susceptible, la relación anterior biológicamente significa que si este número es menor o igual a uno la enfermedad se extingue. mientras que si este número es mayor que uno la enfermedad seguirá siendo permanentemente endémica en la población. ${\displaystyle R_{0}}$

El modelo SIR

Diagrama del modelo SIR con valores iniciales y tasas de infección y recuperación. ${\textstyle S(0)=997,I(0)=3,R(0)=0}$ ${\textstyle \beta =0.4}$ ${\textstyle \gamma =0.04}$

Animación del modelo SIR con valores iniciales y tasa de recuperación . La animación muestra el efecto de reducir la tasa de infección de a . Si no hay medicamentos o vacunas disponibles, sólo es posible reducir la tasa de infección (lo que a menudo se denomina " aplanar la curva ") mediante medidas adecuadas, como el distanciamiento social. ${\textstyle S(0)=997,I(0)=3,R(0)=0}$ ${\textstyle \gamma =0.04}$ ${\textstyle \beta =0.5}$ ${\textstyle \beta =0.12}$

En 1927, WO Kermack y AG McKendrick crearon un modelo en el que consideraban una población fija con sólo tres compartimentos: susceptible, ; infectado, ; y recuperado, . Los compartimentos utilizados para este modelo constan de tres clases: ^[4] ${\displaystyle S(t)}$ ${\displaystyle I(t)}$ ${\displaystyle R(t)}$

• ${\displaystyle S(t)}$se utiliza para representar a los individuos que aún no están infectados con la enfermedad en el momento t, o aquellos susceptibles a la enfermedad de la población.
• ${\displaystyle I(t)}$denota los individuos de la población que han sido infectados con la enfermedad y son capaces de transmitirla a aquellos en la categoría susceptible.
• ${\displaystyle R(t)}$es el compartimento utilizado para los individuos de la población que han sido infectados y luego eliminados de la enfermedad, ya sea por inmunización o por fallecimiento. Aquellos en esta categoría no pueden volver a infectarse ni transmitir la infección a otros.

El flujo de este modelo se puede considerar de la siguiente manera:

${\displaystyle {\color {blue}{{\mathcal {S}}\rightarrow {\mathcal {I}}\rightarrow {\mathcal {R}}}}}$

Usando una población fija, en las tres funciones se resuelve que el valor debe permanecer constante dentro de la simulación, si se utiliza una simulación para resolver el modelo SIR. Alternativamente, la aproximación analítica ^[9] se puede utilizar sin realizar una simulación. El modelo se inicia con valores de , y . Este es el número de personas en las categorías susceptibles, infectadas y eliminadas en un momento igual a cero. Si se supone que el modelo SIR se cumple en todo momento, estas condiciones iniciales no son independientes. ^[9] Posteriormente, el modelo de flujo actualiza las tres variables para cada punto de tiempo con valores establecidos para y . La simulación primero actualiza los infectados de los susceptibles y luego la categoría eliminada se actualiza de la categoría de infectados para el siguiente momento (t=1). Esto describe el flujo de personas entre las tres categorías. Durante una epidemia, la categoría de susceptible no cambia con este modelo, cambia a lo largo de la epidemia y también cambia . Estas variables determinan la duración de la epidemia y deberían actualizarse con cada ciclo. ${\displaystyle N=S(t)+I(t)+R(t)}$ ${\displaystyle N}$ ${\displaystyle S(t=0)}$ ${\displaystyle I(t=0)}$ ${\displaystyle R(t=0)}$ ${\displaystyle \beta }$ ${\displaystyle \gamma }$ ${\displaystyle \beta }$ ${\displaystyle \gamma }$

${\displaystyle {\frac {dS}{dt}}=-{\frac {\beta SI}{N}}}$

${\displaystyle {\frac {dI}{dt}}={\frac {\beta SI}{N}}-\gamma I}$

${\displaystyle {\frac {dR}{dt}}=\gamma I}$

Se hicieron varios supuestos en la formulación de estas ecuaciones: Primero, se debe considerar que un individuo de la población tiene la misma probabilidad que cualquier otro individuo de contraer la enfermedad con una tasa de y una fracción igual de personas con las que un individuo entra en contacto. por unidad de tiempo. Entonces, sea la multiplicación de y . Esta es la probabilidad de transmisión multiplicada por la tasa de contacto. Además, un individuo infectado entra en contacto con personas por unidad de tiempo, mientras que sólo una fracción de ellas es susceptible. Por lo tanto, tenemos que todos los infecciosos pueden infectar a personas susceptibles y, por lo tanto, el número total de susceptibles infectados por infecciosos por unidad de tiempo es . Para la segunda y tercera ecuaciones, considere que la población que sale de la clase susceptible es igual al número que ingresa a la clase infectada. Sin embargo, un número igual a la fracción (que representa la tasa media de recuperación/muerte, o el período infeccioso medio) de infecciosos abandonan esta clase por unidad de tiempo para ingresar a la clase eliminada. Estos procesos que ocurren simultáneamente se conocen como la Ley de Acción de Masas, una idea ampliamente aceptada de que la tasa de contacto entre dos grupos de una población es proporcional al tamaño de cada uno de los grupos involucrados. Finalmente, se supone que la tasa de infección y recuperación es mucho más rápida que la escala temporal de nacimientos y muertes y, por lo tanto, estos factores se ignoran en este modelo. ^[23] ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle \beta }$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle b}$ ${\displaystyle S/N}$ ${\displaystyle abS=\beta S}$ ${\displaystyle \beta SI}$ ${\displaystyle \gamma }$ ${\displaystyle 1/\gamma }$

Soluciones de estado estacionario

La duración esperada de la susceptibilidad será donde refleje el tiempo de vida (esperanza de vida) y refleje el tiempo en estado susceptible antes de infectarse, que se puede simplificar ^[24] a: ${\displaystyle \operatorname {E} [\min(T_{L}\mid T_{S})]}$ ${\displaystyle T_{L}}$ ${\displaystyle T_{S}}$

${\displaystyle \operatorname {E} [\min(T_{L}\mid T_{S})]=\int _{0}^{\infty }e^{-(\mu +\delta )x}\,dx={\frac {1}{\mu +\delta }},}$

de modo que el número de personas susceptibles sea el número de personas que entran en el compartimento susceptible multiplicado por la duración de la susceptibilidad: ${\displaystyle \mu N}$

${\displaystyle S={\frac {\mu N}{\mu +\lambda }}.}$

De manera análoga, el número de personas infectadas en estado estacionario es el número que ingresa al estado infectado desde el estado susceptible (número de susceptibles, multiplicado por la tasa de infección) multiplicado por la duración de la infecciosidad : ${\displaystyle \lambda ={\tfrac {\beta I}{N}},}$ ${\displaystyle {\tfrac {1}{\mu +v}}}$

${\displaystyle I={\frac {\mu N}{\mu +\lambda }}\lambda {\frac {1}{\mu +v}}.}$

Otros modelos compartimentados

Hay muchas modificaciones del modelo SIR, incluidas aquellas que incluyen nacimientos y muertes, donde al recuperarse no hay inmunidad (modelo SIS), donde la inmunidad dura solo un corto período de tiempo (SIRS), donde hay un período latente de la enfermedad donde la persona no es infecciosa (SEIS y SEIR), y donde los bebés pueden nacer con inmunidad (MSIR). Los modelos compartimentales también se pueden utilizar para modelar múltiples grupos de riesgo e incluso la interacción de múltiples patógenos. ^[25]

Variaciones del modelo SIR básico

El modelo SIS

Amarillo=Susceptible, Granate=Infectado

Algunas infecciones, por ejemplo las del resfriado común y la gripe , no confieren ninguna inmunidad duradera. Estas infecciones pueden generar resistencia temporal, pero no otorgan inmunidad a largo plazo una vez que se recuperan de la infección, y los individuos vuelven a ser susceptibles.

Modelo compartimental SIS

Tenemos el modelo:

${\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=-{\frac {\beta SI}{N}}+\gamma I\\[6pt]{\frac {dI}{dt}}&={\frac {\beta SI}{N}}-\gamma I\end{aligned}}}$

Tenga en cuenta que al denotar con N la población total se cumple que:

${\displaystyle {\frac {dS}{dt}}+{\frac {dI}{dt}}=0\Rightarrow S(t)+I(t)=N}$.

Resulta que:

${\displaystyle {\frac {dI}{dt}}=(\beta -\gamma )I-{\frac {\beta }{N}}I^{2}}$,

es decir, la dinámica de las infecciones está regida por una función logística , de modo que : ${\displaystyle \forall I(0)>0}$

${\displaystyle {\begin{aligned}&{\frac {\beta }{\gamma }}\leq 1\Rightarrow \lim _{t\to +\infty }I(t)=0,\\[6pt]&{\frac {\beta }{\gamma }}>1\Rightarrow \lim _{t\to +\infty }I(t)=\left(1-{\frac {\gamma }{\beta }}\right)N.\end{aligned}}}$

Es posible encontrar una solución analítica a este modelo (haciendo una transformación de variables y sustituyéndola en las ecuaciones de campo medio), ^[26] de modo que la tasa de reproducción básica sea mayor que la unidad. La solución se da como ${\displaystyle I=y^{-1}}$

${\displaystyle I(t)={\frac {I_{\infty }}{1+Ve^{-\chi t}}}}$.

¿Dónde está la población infecciosa endémica?, y . Como se supone que el sistema está cerrado, la población susceptible es entonces . ${\displaystyle I_{\infty }=(1-\gamma /\beta )N}$ ${\displaystyle \chi =\beta -\gamma }$ ${\displaystyle V=I_{\infty }/I_{0}-1}$ ${\displaystyle S(t)=N-I(t)}$

Siempre que la naturaleza entera del número de agentes es evidente (poblaciones con menos de decenas de miles de individuos), las fluctuaciones inherentes en el proceso de propagación de enfermedades causadas por agentes discretos generan incertidumbres. ^[27] En este escenario, la evolución de la enfermedad predicha por ecuaciones compartimentales se desvía significativamente de los resultados observados. Estas incertidumbres pueden incluso hacer que la epidemia termine antes de lo previsto por las ecuaciones compartimentales.

Como caso especial, se obtiene la función logística habitual asumiendo . Esto también se puede considerar en el modelo SIR con , es decir, no se realizará ninguna eliminación. Ese es el modelo SI . ^[28] El sistema de ecuaciones diferenciales que se utiliza se reduce así a: ${\displaystyle \gamma =0}$ ${\displaystyle R=0}$ ${\displaystyle S=N-I}$

${\displaystyle {\frac {dI}{dt}}\propto I\cdot (N-I).}$

A largo plazo, en el modelo SI, todos los individuos resultarán infectados.

El modelo SIRD

Diagrama del modelo SIRD con valores iniciales y las tasas de infección , recuperación y mortalidad. ${\displaystyle S(0)=997,I(0)=3,R(0)=0}$ ${\displaystyle \beta =0.4}$ ${\displaystyle \gamma =0.035}$ ${\displaystyle \mu =0.005}$

Animación del modelo SIRD con valores iniciales y tasas de recuperación y mortalidad . La animación muestra el efecto de reducir la tasa de infección de a . Si no hay medicamentos o vacunas disponibles, sólo es posible reducir la tasa de infección (lo que a menudo se denomina "aplanar la curva") mediante medidas como el "distanciamiento social". ${\textstyle S(0)=997,I(0)=3,R(0)=0}$ ${\textstyle \gamma =0.035}$ ${\textstyle \mu =0.005}$ ${\textstyle \beta =0.5}$ ${\textstyle \beta =0.12}$

El modelo Susceptible-Infeccioso-Recuperado-Fallecido diferencia entre Recuperados (es decir, específicamente individuos que han sobrevivido a la enfermedad y ahora son inmunes) y Fallecidos . ^[15] El modelo SIRD tiene soluciones semianalíticas basadas en el método de las cuatro partes. ^[29] Este modelo utiliza el siguiente sistema de ecuaciones diferenciales:

${\displaystyle {\begin{aligned}&{\frac {dS}{dt}}=-{\frac {\beta IS}{N}},\\[6pt]&{\frac {dI}{dt}}={\frac {\beta IS}{N}}-\gamma I-\mu I,\\[6pt]&{\frac {dR}{dt}}=\gamma I,\\[6pt]&{\frac {dD}{dt}}=\mu I,\end{aligned}}}$

¿ Dónde están las tasas de infección, recuperación y mortalidad, respectivamente? ^[30] ${\displaystyle \beta ,\gamma ,\mu }$

El modelo SIRV

El modelo Susceptibles-Infecciosos-Recuperados-Vacunados es un modelo SIR extendido que tiene en cuenta la vacunación de la población susceptible. ^[31] Este modelo utiliza el siguiente sistema de ecuaciones diferenciales:

${\displaystyle {\begin{aligned}&{\frac {dS}{dt}}=-{\frac {\beta (t)IS}{N}}-v(t)S,\\[6pt]&{\frac {dI}{dt}}={\frac {\beta (t)IS}{N}}-\gamma (t)I,\\[6pt]&{\frac {dR}{dt}}=\gamma (t)I,\\[6pt]&{\frac {dV}{dt}}=v(t)S,\end{aligned}}}$

Una caricatura para el modelo SIRV.

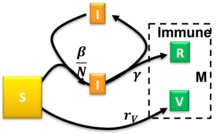
¿Dónde están las tasas de infección, recuperación y vacunación, respectivamente? Para las condiciones iniciales de semitiempo , y razones constantes , el modelo se resolvió aproximadamente. ^[31] La aparición de un estallido pandémico requiere y existe una tasa de vacunación reducida crítica más allá de la cual el tamaño en estado estacionario del compartimento susceptible permanece relativamente cercano a . Las condiciones iniciales arbitrarias que satisfacen se pueden asignar al caso especial resuelto con . ^[31] ${\displaystyle \beta ,\gamma ,v}$ ${\displaystyle S(0)=(1-\eta )N}$ ${\displaystyle I(0)=\eta N}$ ${\displaystyle R(0)=V(0)=0}$ ${\displaystyle k=\gamma (t)/\beta (t)}$ ${\displaystyle b=v(t)/\beta (t)}$ ${\displaystyle k+b<1-2\eta }$ ${\displaystyle b_{c}}$ ${\displaystyle S_{\infty }}$ ${\displaystyle S(0)}$ ${\displaystyle S(0)+I(0)+R(0)+V(0)=N}$ ${\displaystyle R(0)=V(0)=0}$

La solución numérica de este modelo para calcular el número de reproducción en tiempo real de COVID-19 se puede practicar en base a información de las diferentes poblaciones de una comunidad. ^[22] La solución numérica es un método comúnmente utilizado para analizar redes cinéticas complicadas cuando la solución analítica es difícil de obtener o está limitada por requisitos como condiciones de contorno o parámetros especiales. Utiliza ecuaciones recursivas para calcular el siguiente paso convirtiendo la integración numérica en suma de Riemann de pasos de tiempo discretos, por ejemplo, utiliza el principal y la tasa de interés de ayer para calcular el interés de hoy, lo que supone que la tasa de interés es fija durante el día. El cálculo contiene errores proyectados si no se incluyen las correcciones analíticas sobre el tamaño del paso numérico, por ejemplo, cuando la tasa de interés de la recaudación anual se simplifica a 12 veces la tasa mensual, se introduce un error proyectado. Por lo tanto, los resultados calculados conllevarán errores acumulativos cuando el paso de tiempo esté lejos del punto de referencia y se necesite una prueba de convergencia para estimar el error. Sin embargo, este error suele ser aceptable para el ajuste de datos. Cuando se ajusta un conjunto de datos con un paso de tiempo cercano, el error es relativamente pequeño porque el punto de referencia está cerca en comparación con cuando se predice un largo período de tiempo después de un punto de referencia. Una vez que se extrae el tiempo real , se puede comparar con el número de reproducción básico . Antes de la vacunación, brinda a los formuladores de políticas y al público en general una medida de la eficiencia de las actividades de mitigación social, como el distanciamiento social y el uso de mascarillas, simplemente dividiendo . Bajo la vacunación masiva, el objetivo del control de la enfermedad es reducir el número de reproducción efectiva , donde es el número de población susceptible en ese momento y es la población total. Cuando , la propagación decae y los casos diarios de infección disminuyen. ${\displaystyle R_{t}}$ ${\displaystyle R_{t}}$ ${\displaystyle R_{0}}$ ${\displaystyle R_{t}}$ ${\displaystyle {\frac {R_{t}}{R_{0}}}}$ ${\displaystyle R_{e}={\frac {R_{t}S}{N}}<1}$ ${\displaystyle S}$ ${\displaystyle N}$ ${\displaystyle R_{e}<1}$

El modelo MSIR

Para muchas infecciones, incluido el sarampión , los bebés no nacen en el compartimento susceptible, pero son inmunes a la enfermedad durante los primeros meses de vida debido a la protección de los anticuerpos maternos (que pasan a través de la placenta y, además, a través del calostro ). Esto se llama inmunidad pasiva . Este detalle adicional se puede mostrar incluyendo una clase M (para inmunidad derivada de la madre) al comienzo del modelo.

Modelo compartimental MSIR

Para indicar esto matemáticamente, se añade un compartimento adicional, M ( t ) . Esto da como resultado las siguientes ecuaciones diferenciales:

${\displaystyle {\begin{aligned}{\frac {dM}{dt}}&=\Lambda -\delta M-\mu M\\[8pt]{\frac {dS}{dt}}&=\delta M-{\frac {\beta SI}{N}}-\mu S\\[8pt]{\frac {dI}{dt}}&={\frac {\beta SI}{N}}-\gamma I-\mu I\\[8pt]{\frac {dR}{dt}}&=\gamma I-\mu R\end{aligned}}}$

Estado del transportista

Algunas personas que han padecido una enfermedad infecciosa como la tuberculosis nunca se recuperan por completo y continúan siendo portadoras de la infección, aunque ellas mismas no la padezcan. Luego pueden regresar al compartimento infeccioso y sufrir síntomas (como en la tuberculosis) o pueden continuar infectando a otros en su estado de portador, sin sufrir síntomas. El ejemplo más famoso de esto es probablemente el de Mary Mallon , que infectó a 22 personas con fiebre tifoidea . El compartimento portaequipajes está etiquetado como C.

El modelo SEIR

Para muchas infecciones importantes, existe un período de latencia significativo durante el cual los individuos han sido infectados pero aún no son infecciosos. Durante este período el individuo se encuentra en el compartimento E (para expuestos).

Modelo compartimental SEIR

Suponiendo que el período de latencia es una variable aleatoria con distribución exponencial con parámetro (es decir, el período de latencia promedio es ), y suponiendo también la presencia de una dinámica vital con una tasa de natalidad igual a la tasa de mortalidad (de modo que el número total es constante), tenemos el modelo: ${\displaystyle a}$ ${\displaystyle a^{-1}}$ ${\displaystyle \Lambda }$ ${\displaystyle N\mu }$ ${\displaystyle N}$

${\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=\mu N-\mu S-{\frac {\beta IS}{N}}\\[8pt]{\frac {dE}{dt}}&={\frac {\beta IS}{N}}-(\mu +a)E\\[8pt]{\frac {dI}{dt}}&=aE-(\gamma +\mu )I\\[8pt]{\frac {dR}{dt}}&=\gamma I-\mu R.\end{aligned}}}$

Lo hemos hecho , pero esto sólo es constante debido al supuesto simplificador de que las tasas de natalidad y mortalidad son iguales; en general es una variable. ${\displaystyle S+E+I+R=N,}$ ${\displaystyle N}$

Para este modelo, el número de reproducción básico es:

${\displaystyle R_{0}={\frac {a}{\mu +a}}{\frac {\beta }{\mu +\gamma }}.}$

De manera similar al modelo SIR, en este caso también tenemos un equilibrio libre de enfermedades ( N ,0,0,0) y un equilibrio endémico EE, y se puede demostrar que, independientemente de las condiciones iniciales biológicamente significativas

${\displaystyle \left(S(0),E(0),I(0),R(0)\right)\in \left\{(S,E,I,R)\in [0,N]^{4}:S\geq 0,E\geq 0,I\geq 0,R\geq 0,S+E+I+R=N\right\}}$

sostiene que:

${\displaystyle R_{0}\leq 1\Rightarrow \lim _{t\to +\infty }\left(S(t),E(t),I(t),R(t)\right)=DFE=(N,0,0,0),}$

${\displaystyle R_{0}>1,I(0)>0\Rightarrow \lim _{t\to +\infty }\left(S(t),E(t),I(t),R(t)\right)=EE.}$

En caso de que la tasa de contacto varíe periódicamente, la condición para el atractivo global de DFE es que se utilice el siguiente sistema lineal con coeficientes periódicos: ${\displaystyle \beta (t)}$

${\displaystyle {\begin{aligned}{\frac {dE_{1}}{dt}}&=\beta (t)I_{1}-(\gamma +a)E_{1}\\[8pt]{\frac {dI_{1}}{dt}}&=aE_{1}-(\gamma +\mu )I_{1}\end{aligned}}}$

es estable (es decir, tiene sus valores propios de Floquet dentro del círculo unitario en el plano complejo).

El modelo SEIS

El modelo SEIS es como el modelo SEIR (arriba), excepto que al final no se adquiere inmunidad.

${\displaystyle {\color {blue}{{\mathcal {S}}\to {\mathcal {E}}\to {\mathcal {I}}\to {\mathcal {S}}}}}$

En este modelo, una infección no deja inmunidad, por lo que los individuos que se han recuperado vuelven a ser susceptibles y regresan al compartimento S ( t ). Las siguientes ecuaciones diferenciales describen este modelo:

${\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=\Lambda -{\frac {\beta SI}{N}}-\mu S+\gamma I\\[6pt]{\frac {dE}{dt}}&={\frac {\beta SI}{N}}-(\epsilon +\mu )E\\[6pt]{\frac {dI}{dt}}&=\varepsilon E-(\gamma +\mu )I\end{aligned}}}$

El modelo MSEIR

Para el caso de una enfermedad, con los factores de inmunidad pasiva, y un periodo de latencia existe el modelo MSEIR.

${\displaystyle \color {blue}{{\mathcal {M}}\to {\mathcal {S}}\to {\mathcal {E}}\to {\mathcal {I}}\to {\mathcal {R}}}}$

${\displaystyle {\begin{aligned}{\frac {dM}{dt}}&=\Lambda -\delta M-\mu M\\[6pt]{\frac {dS}{dt}}&=\delta M-{\frac {\beta SI}{N}}-\mu S\\[6pt]{\frac {dE}{dt}}&={\frac {\beta SI}{N}}-(\varepsilon +\mu )E\\[6pt]{\frac {dI}{dt}}&=\varepsilon E-(\gamma +\mu )I\\[6pt]{\frac {dR}{dt}}&=\gamma I-\mu R\end{aligned}}}$

El modelo MSEIRS

Un modelo MSEIRS es similar al MSEIR, pero la inmunidad en la clase R sería temporal, de modo que los individuos recuperarían su susceptibilidad cuando terminara la inmunidad temporal.

${\displaystyle {\color {blue}{{\mathcal {M}}\to {\mathcal {S}}\to {\mathcal {E}}\to {\mathcal {I}}\to {\mathcal {R}}\to {\mathcal {S}}}}}$

Tarifas de contacto variables

Es bien sabido que la probabilidad de contraer una enfermedad no es constante en el tiempo. A medida que avanza una pandemia, las reacciones a la misma pueden cambiar las tasas de contacto que se suponen constantes en los modelos más simples. Contramedidas como máscaras, distanciamiento social y bloqueo alterarán la tasa de contacto de manera de reducir la velocidad de la pandemia.

Además, algunas enfermedades son estacionales, como los virus del resfriado común , que son más frecuentes durante el invierno. En el caso de enfermedades infantiles como el sarampión, las paperas y la rubéola, existe una fuerte correlación con el calendario escolar, de modo que durante las vacaciones escolares la probabilidad de contraer dichas enfermedades disminuye drásticamente. Como consecuencia, para muchas clases de enfermedades, se debe considerar una fuerza de infección con una tasa de contacto que varía periódicamente ("estacionalmente").

${\displaystyle F=\beta (t){\frac {I}{N}},\quad \beta (t+T)=\beta (t)}$

con periodo T igual a un año.

Así, nuestro modelo se convierte en

${\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=\mu N-\mu S-\beta (t){\frac {I}{N}}S\\[8pt]{\frac {dI}{dt}}&=\beta (t){\frac {I}{N}}S-(\gamma +\mu )I\end{aligned}}}$

(la dinámica de los recuperados se desprende fácilmente de ), es decir, un conjunto no lineal de ecuaciones diferenciales con parámetros que varían periódicamente. Es bien sabido que esta clase de sistemas dinámicos puede sufrir fenómenos muy interesantes y complejos de resonancia paramétrica no lineal. Es fácil ver que si: ${\displaystyle R=N-S-I}$

${\displaystyle {\frac {1}{T}}\int _{0}^{T}{\frac {\beta (t)}{\mu +\gamma }}\,dt<1\Rightarrow \lim _{t\to +\infty }(S(t),I(t))=DFE=(N,0),}$

mientras que si la integral es mayor que uno la enfermedad no desaparecerá y puede haber tales resonancias. Por ejemplo, considerando la tasa de contacto que varía periódicamente como la 'entrada' del sistema, se tiene que la salida es una función periódica cuyo período es un múltiplo del período de la entrada. Esto permitió contribuir a explicar los brotes epidémicos polianuales (típicamente bienales) de algunas enfermedades infecciosas como una interacción entre el período de oscilaciones de la tasa de contacto y el pseudoperíodo de oscilaciones amortiguadas cerca del equilibrio endémico. Sorprendentemente, en algunos casos, el comportamiento también puede ser casi periódico o incluso caótico.

Modelo SIR con difusión.

Los modelos compartimentales espaciotemporales describen no el número total, sino la densidad de personas susceptibles/infecciosas/recuperadas. En consecuencia, también permiten modelar la distribución de personas infectadas en el espacio. En la mayoría de los casos, esto se hace combinando el modelo SIR con una ecuación de difusión.

${\displaystyle {\begin{aligned}&\partial _{t}S=D_{S}\nabla ^{2}S-{\frac {\beta IS}{N}},\\[6pt]&\partial _{t}I=D_{I}\nabla ^{2}I+{\frac {\beta IS}{N}}-\gamma I,\\[6pt]&\partial _{t}R=D_{R}\nabla ^{2}R+\gamma I,\end{aligned}}}$^[32]

donde , y son constantes de difusión. De este modo se obtiene una ecuación de reacción-difusión. (Tenga en cuenta que, por razones dimensionales, el parámetro debe cambiarse en comparación con el modelo SIR simple). Los primeros modelos de este tipo se han utilizado para modelar la propagación de la peste negra en Europa. ^[33] Se han utilizado extensiones de este modelo para incorporar, por ejemplo, efectos de intervenciones no farmacéuticas como el distanciamiento social. ^[34] ${\displaystyle D_{S}}$ ${\displaystyle D_{I}}$ ${\displaystyle D_{R}}$ ${\displaystyle \beta }$

Modelo SEIR de subpoblación interactiva

Como los contactos sociales, la gravedad y la letalidad de la enfermedad, así como la eficacia de las medidas profilácticas, pueden diferir sustancialmente entre subpoblaciones que interactúan, por ejemplo, los ancianos versus los jóvenes, se pueden usar modelos SEIR separados para cada subgrupo que están conectados entre sí a través de vínculos de interacción. ^[32] Estos modelos SEIR de subpoblaciones interactivas se han utilizado para modelar la pandemia de COVID-19 a escala continental para desarrollar estrategias de vacunación personalizadas, aceleradas y dirigidas a subpoblaciones ^[35] que prometen un acortamiento de la pandemia y una reducción de los recuentos de casos y muertes. en un contexto de acceso limitado a las vacunas durante una ola de variantes preocupantes del virus.

Modelo SIR en Redes

El modelo SIR se ha estudiado en redes de diversos tipos para modelar una forma de conexión más realista que la condición de mezcla homogénea que habitualmente se requiere. Un modelo simple para epidemias en redes en el que un individuo tiene una probabilidad p de ser infectado por cada uno de sus vecinos infectados en un lapso de tiempo determinado conduce a resultados similares a la formación de componentes gigantes en los gráficos aleatorios de Erdos Renyi . ^[36]

Modelo SIR SS : combinación de SIR con modelado de estrés social

La dinámica de las epidemias depende de cómo cambia el comportamiento de las personas con el tiempo. Por ejemplo, al comienzo de la epidemia, la gente es ignorante y descuidada, luego, después del estallido de la epidemia y la alarma, comienzan a cumplir con las diversas restricciones y la propagación de la epidemia puede disminuir. Con el tiempo, algunas personas se cansan o frustran por las restricciones y dejan de seguirlas (agotamiento), especialmente si el número de casos nuevos disminuye. Después de descansar un tiempo, pueden volver a seguir las restricciones. Pero durante esta pausa puede llegar la segunda ola y volverse incluso más fuerte que la primera. Se debe considerar la dinámica social . Los modelos de física social del estrés social complementan los modelos clásicos de epidemias. ^[37]

Se muestra un ejemplo del uso del modelo SIR numérico para ajustar los datos de COVID-19 (de los CDC de EE. UU.) en el estado de Ohio, EE. UU., ajustados utilizando el modelo SIR y SIRV. Tenga en cuenta que aunque el modelo SIR puede modelar una onda individual, un modelo más complejo como SIR _SS modelaría mejor ondas múltiples. ^{[21] [22]} ${\displaystyle R_{t}}$

El modelo SIR-estrés social (SIR _SS ) más simple se organiza de la siguiente manera. Los individuos susceptibles (S) se pueden dividir en tres subgrupos según los tipos de comportamiento: ignorantes o inconscientes de la epidemia (S _ign ), racionalmente resistentes (S _res ), y exhaustos (S _exh ) que no reaccionan a los estímulos externos. (Ésta es una especie de período refractario). En otras palabras: S(t) = S _ign (t) + S _res (t) + S _exh (t). Simbólicamente, el modelo de estrés social se puede representar mediante el "esquema de reacción" (donde I denota los individuos infectados):

• ${\displaystyle {\color {blue}{{\mathcal {S_{ign}}}+2{\mathcal {I}}\to {\mathcal {S_{res}}}+2{\mathcal {I}}}}}$– reacción de movilización (la forma autocatalítica aquí significa que la velocidad de transición es proporcional al cuadrado de la fracción I infectada);
• ${\displaystyle {\color {blue}{{\mathcal {S_{res}}}\to {\mathcal {S_{exh}}}}}}$– proceso de agotamiento debido a la fatiga causada por las restricciones antiepidémicas;
• ${\displaystyle {\color {blue}{{\mathcal {S_{exh}}}\to {\mathcal {S_{ign}}}}}}$– relajación lenta hasta el estado inicial (fin del período refractario).

La principal reacción epidémica SIR.

• ${\displaystyle {\color {blue}{{\mathcal {S_{...}}}+{\mathcal {I}}\to {\mathcal {2I}}}}}$

tiene diferentes constantes de velocidad de reacción para S _ign , S _res y _Sexh . Presumiblemente, para S _res , es menor que para _Sign y _Sign . ${\displaystyle \beta }$ ${\displaystyle \beta }$

Las diferencias entre países se concentran en dos constantes cinéticas: la tasa de movilización y la tasa de agotamiento calculadas para la epidemia de COVID-19 en 13 países. ^[37] Estas constantes para esta epidemia en todos los países se pueden extraer ajustando el modelo SIR _SS a los datos disponibles públicamente ^[38]

La ecuación KdV-SIR

Basado en el modelo SIR clásico, se ha propuesto una ecuación Korteweg-de Vries (KdV)-SIR y su solución analítica para ilustrar la dinámica fundamental de una ola epidémica, la dependencia de las soluciones de los parámetros y la dependencia de los horizontes de previsibilidad de varios factores. tipos de soluciones. ^[39] La ecuación KdV-SIR se escribe de la siguiente manera:

${\displaystyle {\frac {d^{2}I}{dt}}-\sigma _{o}^{2}I+{\frac {3}{2}}{\frac {\sigma _{o}^{2}}{I_{max}}}I^{2}=0}$.

Aquí,

${\displaystyle \sigma _{o}=\gamma (R_{o}-1)}$,

${\displaystyle R_{o}={\frac {\beta }{\gamma }}{\frac {S_{o}}{N}}}$,

y

${\displaystyle I_{max}={\frac {S_{o}}{2}}{\frac {(R_{o}-1)^{2}}{R_{o}^{2}}}}$.

${\displaystyle S_{o}}$Indica el valor inicial de la variable de estado . Los parámetros (σ-cero) y (R-cero) son la tasa de crecimiento relativo independiente del tiempo y el número de reproducción básico, respectivamente. presenta el máximo de las variables estatales (para el número de personas infectadas). Una solución analítica a la ecuación KdV-SIR se escribe de la siguiente manera: ${\displaystyle S}$ ${\displaystyle \sigma _{o}}$ ${\displaystyle R_{o}}$ ${\displaystyle I_{max}}$ ${\displaystyle I}$

${\displaystyle I=I_{max}sech^{2}\left({\frac {\sigma _{o}}{2}}t\right)}$,

que representa una solución de onda solitaria.

Modelando la vacunación

El modelo SIR se puede modificar para modelar la vacunación. ^[40] Por lo general, estos introducen un compartimento adicional al modelo SIR, para personas vacunadas. A continuación se muestran algunos ejemplos. ${\displaystyle V}$

Vacunar a los recién nacidos

En presencia de enfermedades transmisibles, una de las principales tareas es erradicarla mediante medidas de prevención y, si es posible, mediante el establecimiento de un programa de vacunación masiva. Consideremos una enfermedad contra la cual se vacuna al recién nacido (con una vacuna que le confiere inmunidad de por vida) a un ritmo : ${\displaystyle P\in (0,1)}$

${\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=\nu N(1-P)-\mu S-\beta {\frac {I}{N}}S\\[8pt]{\frac {dI}{dt}}&=\beta {\frac {I}{N}}S-(\mu +\gamma )I\\[8pt]{\frac {dV}{dt}}&=\nu NP-\mu V\end{aligned}}}$

¿ Dónde está la clase de sujetos vacunados? Es inmediato demostrar que: ${\displaystyle V}$

${\displaystyle \lim _{t\to +\infty }V(t)=NP,}$

así nos ocuparemos del comportamiento a largo plazo de y , para lo cual se sostiene que: ${\displaystyle S}$ ${\displaystyle I}$

${\displaystyle R_{0}(1-P)\leq 1\Rightarrow \lim _{t\to +\infty }\left(S(t),I(t)\right)=DFE=\left(N\left(1-P\right),0\right)}$

${\displaystyle R_{0}(1-P)>1,\quad I(0)>0\Rightarrow \lim _{t\to +\infty }\left(S(t),I(t)\right)=EE=\left({\frac {N}{R_{0}(1-P)}},N\left(R_{0}(1-P)-1\right)\right).}$

En otras palabras, si

${\displaystyle P<P^{*}=1-{\frac {1}{R_{0}}}}$

el programa de vacunación no logra erradicar la enfermedad, por el contrario, seguirá siendo endémica, aunque en niveles más bajos que en caso de ausencia de vacunas. Esto significa que el modelo matemático sugiere que para una enfermedad cuyo número de reproducción básico puede llegar a 18, se debería vacunar al menos al 94,4% de los recién nacidos para erradicar la enfermedad.

Vacunación e información

Las sociedades modernas se enfrentan al desafío de la exención "racional", es decir, la decisión de la familia de no vacunar a los niños como consecuencia de una comparación "racional" entre el riesgo percibido de infección y el de sufrir daños por la vacuna. Para evaluar si este comportamiento es realmente racional, es decir, si puede conducir igualmente a la erradicación de la enfermedad, se puede simplemente suponer que la tasa de vacunación es una función creciente del número de sujetos infecciosos:

${\displaystyle P=P(I),\quad P'(I)>0.}$

En tal caso la condición de erradicación pasa a ser:

${\displaystyle P(0)\geq P^{*},}$

es decir, la tasa de vacunación inicial debería ser mayor que el umbral de "vacunación obligatoria", que, en caso de exención, no se puede mantener. Por lo tanto, la exención "racional" podría ser miope, ya que se basa únicamente en la baja incidencia actual debido a la alta cobertura de vacunación, y en lugar de ello toma en cuenta el futuro resurgimiento de la infección debido a la disminución de la cobertura.

Vacunación de no recién nacidos

En caso de que también existan vacunaciones de no recién nacidos a una tasa ρ, la ecuación para el sujeto susceptible y vacunado debe modificarse de la siguiente manera:

${\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=\mu N(1-P)-\mu S-\rho S-\beta {\frac {I}{N}}S\\[8pt]{\frac {dV}{dt}}&=\mu NP+\rho S-\mu V\end{aligned}}}$

conduciendo a la siguiente condición de erradicación:

${\displaystyle P\geq 1-\left(1+{\frac {\rho }{\mu }}\right){\frac {1}{R_{0}}}}$

Estrategia de vacunación por pulsos

Esta estrategia vacuna repetidamente a una cohorte de edad definida (como niños pequeños o ancianos) en una población susceptible a lo largo del tiempo. Con esta estrategia, el bloque de individuos susceptibles se elimina inmediatamente, lo que permite eliminar una enfermedad infecciosa (como el sarampión) de toda la población. Cada T unidades de tiempo se vacuna a una fracción constante p de sujetos susceptibles en un tiempo relativamente corto (con respecto a la dinámica de la enfermedad). Esto conduce a las siguientes ecuaciones diferenciales impulsivas para los sujetos susceptibles y vacunados:

${\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=\mu N-\mu S-\beta {\frac {I}{N}}S,\quad S(nT^{+})=(1-p)S(nT^{-}),&&n=0,1,2,\ldots \\[8pt]{\frac {dV}{dt}}&=-\mu V,\quad V(nT^{+})=V(nT^{-})+pS(nT^{-}),&&n=0,1,2,\ldots \end{aligned}}}$

Es fácil ver que poniendo I = 0 se obtiene que la dinámica de los sujetos susceptibles viene dada por:

${\displaystyle S^{*}(t)=1-{\frac {p}{1-(1-p)E^{-\mu T}}}E^{-\mu MOD(t,T)}}$

y que la condición de erradicación es:

${\displaystyle R_{0}\int _{0}^{T}S^{*}(t)\,dt<1}$

La influencia de la edad: modelos estructurados por edades

La edad tiene una profunda influencia en la tasa de propagación de enfermedades en una población, especialmente en la tasa de contacto. Esta tasa resume la efectividad de los contactos entre sujetos susceptibles e infecciosos. Teniendo en cuenta las edades de las clases epidémicas (para limitarnos al esquema susceptible-infeccioso-eliminado) tales que: ${\displaystyle s(t,a),i(t,a),r(t,a)}$

${\displaystyle S(t)=\int _{0}^{a_{M}}s(t,a)\,da}$

${\displaystyle I(t)=\int _{0}^{a_{M}}i(t,a)\,da}$

${\displaystyle R(t)=\int _{0}^{a_{M}}r(t,a)\,da}$

(donde está la edad máxima admisible) y su dinámica no se describe, como podría pensarse, mediante ecuaciones diferenciales parciales "simples", sino mediante ecuaciones integrodiferenciales : ${\displaystyle a_{M}\leq +\infty }$

${\displaystyle \partial _{t}s(t,a)+\partial _{a}s(t,a)=-\mu (a)s(a,t)-s(a,t)\int _{0}^{a_{M}}k(a,a_{1};t)i(a_{1},t)\,da_{1}}$

${\displaystyle \partial _{t}i(t,a)+\partial _{a}i(t,a)=s(a,t)\int _{0}^{a_{M}}{k(a,a_{1};t)i(a_{1},t)da_{1}}-\mu (a)i(a,t)-\gamma (a)i(a,t)}$

${\displaystyle \partial _{t}r(t,a)+\partial _{a}r(t,a)=-\mu (a)r(a,t)+\gamma (a)i(a,t)}$

dónde:

${\displaystyle F(a,t,i(\cdot ,\cdot ))=\int _{0}^{a_{M}}k(a,a_{1};t)i(a_{1},t)\,da_{1}}$

es la fuerza de la infección, que, por supuesto, dependerá, aunque el núcleo de contacto, de las interacciones entre las edades. ${\displaystyle k(a,a_{1};t)}$

La complejidad se suma a las condiciones iniciales para los recién nacidos (es decir, para a=0), que son sencillas de infectar y eliminadas:

${\displaystyle i(t,0)=r(t,0)=0}$

pero que son no locales para la densidad de recién nacidos susceptibles:

${\displaystyle s(t,0)=\int _{0}^{a_{M}}\left(\varphi _{s}(a)s(a,t)+\varphi _{i}(a)i(a,t)+\varphi _{r}(a)r(a,t)\right)\,da}$

¿ Dónde están las fertilidades de los adultos? ${\displaystyle \varphi _{j}(a),j=s,i,r}$

Además, definiendo ahora la densidad de la población total se obtiene: ${\displaystyle n(t,a)=s(t,a)+i(t,a)+r(t,a)}$

${\displaystyle \partial _{t}n(t,a)+\partial _{a}n(t,a)=-\mu (a)n(a,t)}$

En el caso más simple de igualdad de fecundidades en las tres clases epidémicas, tenemos que para tener equilibrio demográfico debe cumplirse la siguiente condición necesaria y suficiente que vincula la fecundidad con la mortalidad : ${\displaystyle \varphi (.)}$ ${\displaystyle \mu (a)}$

${\displaystyle 1=\int _{0}^{a_{M}}\varphi (a)\exp \left(-\int _{0}^{a}{\mu (q)dq}\right)\,da}$

y el equilibrio demográfico es

${\displaystyle n^{*}(a)=C\exp \left(-\int _{0}^{a}\mu (q)\,dq\right),}$

asegurando automáticamente la existencia de la solución libre de enfermedades:

${\displaystyle DFS(a)=(n^{*}(a),0,0).}$

Un número de reproducción básico se puede calcular como el radio espectral de un operador funcional apropiado.

Otras consideraciones dentro de los modelos epidémicos compartimentales

Transmisión vertical

En el caso de algunas enfermedades como el SIDA y la hepatitis B, es posible que los hijos de padres infectados nazcan infectados. Esta transmisión de la enfermedad desde la madre se conoce como transmisión vertical. La afluencia de miembros adicionales a la categoría de infectados se puede considerar dentro del modelo incluyendo una fracción de los miembros recién nacidos en el compartimento infectado. ^[41]

Transmisión vectorial

Las enfermedades que se transmiten indirectamente de persona a persona, es decir, la malaria transmitida por mosquitos, se transmiten a través de un vector. En estos casos, la infección se transfiere de humanos a insectos y un modelo epidémico debe incluir ambas especies, y generalmente requiere muchos más compartimentos que un modelo de transmisión directa. ^{[41] [42]}

Otros

Otros sucesos que pueden necesitar ser considerados al modelar una epidemia incluyen aspectos como los siguientes: ^[41]

• Mezcla no homogénea
• Infectividad variable
• Distribuciones que son espacialmente no uniformes
• Enfermedades causadas por macroparásitos.

Modelos epidémicos deterministas versus estocásticos

Es importante enfatizar que los modelos deterministas presentados aquí son válidos sólo en el caso de poblaciones suficientemente grandes y, como tales, deben usarse con cautela. ^{[43] [44]}

Para ser más precisos, estos modelos sólo son válidos en el límite termodinámico , donde la población es efectivamente infinita. En los modelos estocásticos, el equilibrio endémico a largo plazo derivado anteriormente no se cumple, ya que existe una probabilidad finita de que el número de individuos infectados caiga por debajo de uno en un sistema. Entonces, en un sistema verdadero, es posible que el patógeno no se propague, ya que ningún huésped resultará infectado. Pero, en los modelos deterministas de campo medio, el número de infectados puede tomar valores reales, es decir, no enteros, de huéspedes infectados, y el número de huéspedes en el modelo puede ser menor que uno, pero mayor que cero, permitiendo así la patógeno en el modelo para propagarse. La confiabilidad de los modelos compartimentales se limita a aplicaciones compartimentales.

Una de las posibles extensiones de los modelos de campo medio considera la propagación de epidemias en una red basada en conceptos de la teoría de la percolación . ^[36] Los modelos epidémicos estocásticos se han estudiado en diferentes redes ^{[45] [46] [47]} y, más recientemente, se han aplicado a la pandemia de COVID-19 . ^[48]

Ver también

• Modelización matemática en epidemiología.
• Aplanar la curva
• Problema de unidad de área modificable
• Matriz de próxima generación
• Evaluación de riesgos
• Tasa de ataque
• Lista de modelos de simulación de COVID-19

Referencias

1. Ross R (1 de febrero de 1916). "Una aplicación de la teoría de las probabilidades al estudio de la patometría a priori.—Parte I". Actas de la Royal Society de Londres. Serie A, que contiene artículos de carácter físico y matemático . 92 (638): 204–230. Código Bib : 1916RSPSA..92..204R. doi : 10.1098/rspa.1916.0007 .
2. Ross R, Hudson H (3 de mayo de 1917). "Una aplicación de la teoría de las probabilidades al estudio de la patometría a priori. Parte II". Actas de la Royal Society de Londres. Serie A, que contiene artículos de carácter físico y matemático . 93 (650): 212–225. Código bibliográfico : 1917RSPSA..93..212R. doi : 10.1098/rspa.1917.0014 .
3. Ross R, Hudson H (1917). "Una aplicación de la teoría de las probabilidades al estudio de la patometría a priori. Parte III". Actas de la Royal Society de Londres. Serie A, que contiene artículos de carácter físico y matemático . 89 (621): 225–240. Código Bib : 1917RSPSA..93..225R. doi : 10.1098/rspa.1917.0015 .
4. Kermack WO, McKendrick AG (1927). "Una contribución a la teoría matemática de las epidemias". Actas de la Royal Society de Londres. Serie A, que contiene artículos de carácter físico y matemático . 115 (772): 700–721. Código Bib : 1927RSPSA.115..700K. doi : 10.1098/rspa.1927.0118 .
5. Kendall DG (1956). "Epidemias deterministas y estocásticas en poblaciones cerradas". Aportes a la Biología y Problemas de Salud . vol. 4. Prensa de la Universidad de California. págs. 149-165. doi :10.1525/9780520350717-011. ISBN 978-0-520-35071-7. Señor  0084936. Zbl  0070.15101.
6. Engelmann, Lucas (30 de agosto de 2021). "Una caja, un abrevadero y canicas: cómo la teoría de la epidemia de Reed-Frost dio forma al razonamiento epidemiológico en el siglo XX". Historia y Filosofía de las Ciencias de la Vida . 43 (3): 105. doi :10.1007/s40656-021-00445-z. ISSN  1742-6316. PMC 8404547 . PMID  34462807. 
7. Harko T, Lobo FS, Mak MK (2014). "Soluciones analíticas exactas del modelo epidémico Susceptibles-Infectados-Recuperados (SIR) y del modelo SIR con iguales tasas de mortalidad y natalidad". Matemáticas Aplicadas y Computación . 236 : 184-194. arXiv : 1403.2160 . Código Bib : 2014arXiv1403.2160H. doi :10.1016/j.amc.2014.03.030. S2CID  14509477.
8. Beckley R, Weatherspoon C, Alexander M, Chandler M, Johnson A, Bhatt GS (2013). "Modelado de epidemias con ecuaciones diferenciales" (PDF) . Informe interno de la Universidad Estatal de Tennessee . Consultado el 19 de julio de 2020 .
9. Kröger M, Schlickeiser R (2020). "Solución analítica del modelo SIR para la evolución temporal de epidemias. Parte A: Factor de reproducción independiente del tiempo". Revista de Física A. 53 (50): 505601. Código bibliográfico : 2020JPhA...53X5601K. doi : 10.1088/1751-8121/abc65d . S2CID  225555567.
10. Schlickeiser R, Kröger M (2021). "Solución analítica del modelo SIR para la evolución temporal de epidemias. Parte B: Caso semitemporal". Revista de Física A. 54 (17): 175601. Código bibliográfico : 2021JPhA...54q5601S. doi : 10.1088/1751-8121/abed66 . hdl : 20.500.11850/479548 .
11. Yang W, Zhang D, Peng L, Zhuge C, Hong L (2020). "Evaluación racional de varios modelos epidémicos basados ​​en los datos de COVID-19 de China". arXiv : 2003.05666v1 [q-bio.PE].
12. Simón, Cory (2020). "El modelo dinámico SIR de transmisión de enfermedades infecciosas y su analogía con la cinética química". PeerJ Química Física . 2 (2): e14. doi : 10.7717/peerj-pchem.14 .
13. Krylova O, Earn DJ (julio de 2013). "Efectos de la distribución del período infeccioso sobre las transiciones previstas en la dinámica de las enfermedades infantiles". Revista de la Royal Society, Interfaz . 10 (84): 20130098. doi : 10.1098/rsif.2013.0098 . PMC 3673147 . PMID  23676892. 
14. Hethcote H (2000). "Las matemáticas de las enfermedades infecciosas". Revisión SIAM . 42 (4): 599–653. Código Bib : 2000SIAMR..42..599H. doi :10.1137/s0036144500371907. S2CID  10836889.
15. Bailey, Norman TJ (1975). La teoría matemática de las enfermedades infecciosas y sus aplicaciones (2ª ed.). Londres: Griffin. ISBN 0-85264-231-8.
16. Sonia Altizer; Nunn, Charles (2006). Enfermedades infecciosas en primates: comportamiento, ecología y evolución . Serie Oxford sobre Ecología y Evolución. Oxford [Oxfordshire]: Oxford University Press. ISBN 0-19-856585-2.
17. Wolfram Research, Inc. "Mathematica, versión 12.1". Champaign Illinois, 2020.
18. Capasso V (1993). Estructura matemática de los sistemas epidémicos . Berlín: Springer. ISBN 3-540-56526-4.
19. Miller JC (septiembre de 2012). "Una nota sobre la derivación del tamaño final de la epidemia". Boletín de Biología Matemática . 74 (9): 2125–2141. doi :10.1007/s11538-012-9749-6. PMC 3506030 . PMID  22829179. Sección 4.1 
20. Miller JC (febrero de 2017). "Los modelos matemáticos de la enfermedad SIR se propagan mediante rutas de transmisión sexual y no sexual combinadas". Modelado de enfermedades infecciosas . 2 (1): 35–55. doi :10.1016/j.idm.2016.12.003. PMC 5963332 . PMID  29928728. Sección 2.1.3 
21. Hart KD, Thompson C, Burger C, Hardwick D, Michaud AH, Bulushi A, Pridemore C, Ward C, Chen J (2021). "Aprendizaje remoto del análisis cinético de COVID-19 en una clase de laboratorio de química física". ACS Omega . 6 (43): 29223–29232. doi :10.1021/acsomega.1c04842. PMC 8547164 . PMID  34723043. 
22. Smith DK, Lauro K, Kelly D, Fish J, Lintelman E, McEwen D, Smith C, Stecz M, Ambagaspitiya TD, Chen J (2022). "Docencia de laboratorio de química física de pregrado con análisis cinético de COVID-19 en Estados Unidos". Revista de Educación Química . 99 (10): 3471–3477. Código Bib : 2022JChEd..99.3471S. doi :10.1021/acs.jchemed.2c00416. PMC 9799982 . PMID  36589277. S2CID  251484056. 
23. Padua RN, Tulang AB (2 de diciembre de 2010). "Un modelo epidemiológico dependiente de la densidad para la propagación de enfermedades infecciosas". Revista Liceo de Investigación en Educación Superior . 6 (2). doi : 10.7828/ljher.v6i2.62.
24. Mayo RM , Anderson B (24 de septiembre de 1992). Enfermedades infecciosas de los humanos: dinámica y control (edición revisada). Oxford: Prensa de la Universidad de Oxford. ISBN 978-0-19-854040-3.
25. von Csefalvay, Chris (1 de enero de 2023), von Csefalvay, Chris (ed.), "Factores del huésped", Modelado computacional de enfermedades infecciosas , Academic Press, págs. 93-119, doi : 10.1016/b978-0- 32-395389-4.00012-8 , ISBN 978-0-323-95389-4
26. Hethcote HW (1989). "Tres modelos epidemiológicos básicos". En Levin SA, Hallam TG, Gross LJ (eds.). Ecología Matemática Aplicada . Biomatemáticas. vol. 18. Berlín: Springer. págs. 119-144. doi :10.1007/978-3-642-61317-3_5. ISBN 3-540-19465-7.
27. Nakamura, director general; Cardoso, GC; Martínez, AS (2020). "Ecuaciones epidémicas susceptibles-infecciosas-susceptibles mejoradas basadas en incertidumbres y funciones de autocorrelación". Ciencia abierta de la Royal Society . 7 (2): 191504. Código bibliográfico : 2020RSOS....791504N. doi :10.1098/rsos.191504. PMC 7062106 . PMID  32257317. 
28. "(p. 19) El modelo SI" (PDF) .
29. Al-Raeei, Marwan (2021). "El número básico de reproducción de la pandemia del nuevo coronavirus con mortalidad para India, República Árabe Siria, Estados Unidos, Yemen, China, Francia, Nigeria y Rusia con diferente tasa de casos". Epidemiología clínica y salud global . 9 : 147-149. doi :10.1016/j.cegh.2020.08.005. ISSN  2452-0918. PMC 7438206 . PMID  32844133. 
30. La primera y segunda ecuaciones diferenciales se transforman y se llevan a la misma forma que para el modelo SIR anterior.
31. Schlickeiser R, Kröger M (2021). "Modelado analítico de la evolución temporal de los brotes epidémicos contabilizando las vacunas". Física . 3 (2): 386. Bibcode : 2021Physi...3..386S. doi : 10.3390/física3020028 . hdl : 20.500.11850/487253 . S2CID  233589998.
32. Hunziker P (24 de julio de 2021). "Vacunación Covid-19 de dosis personalizada en una ola de variantes de virus preocupantes: cambiar la eficacia individual por el beneficio social". Nanomedicina de precisión . 4 (3): 805–820. doi : 10.33218/001c.26101 .
33. Noble JV (agosto de 1974). "Desarrollo geográfico y temporal de las plagas". Naturaleza . 250 (5469): 726–729. Código Bib :1974Natur.250..726N. doi :10.1038/250726a0. PMID  4606583. S2CID  4210869.
34. Te Vrugt M, Bickmann J, Wittkowski R (noviembre de 2020). "Efectos del distanciamiento social y el aislamiento en la propagación de epidemias modelados mediante la teoría funcional de la densidad dinámica". Comunicaciones de la naturaleza . 11 (1): 5576. arXiv : 2003.13967 . Código Bib : 2020NatCo..11.5576T. doi : 10.1038/s41467-020-19024-0 . PMC 7643184 . PMID  33149128. 
35. Hunziker P (7 de marzo de 2021). "Estrategias de vacunación para minimizar la pérdida de vidas por Covid-19 en una Europa carente de vacunas". medRxiv 10.1101/2021.01.29.21250747 . 
36. Croccolo F, Roman HE (octubre de 2020). "Propagación de infecciones en gráficos aleatorios: un modelo de tipo percolación para COVID-19". Caos, Solitones y Fractales . 139 : 110077. arXiv : 2006.10490 . Código Bib : 2020CSF...13910077C. doi : 10.1016/j.caos.2020.110077. PMC 7332959 . PMID  32834619. S2CID  219792089. 
37. Kastalskiy, IA; Pankratova, EV; Mirkes, EM; et al. (2021). "El estrés social impulsa la dinámica de múltiples ondas de los brotes de COVID-19". Informes científicos . 11 (1): 22497. arXiv : 2106.08966 . Código Bib : 2021NatSR..1122497K. doi : 10.1038/s41598-021-01317-z . PMC 8602246 . PMID  34795311. 
38. El repositorio de datos COVID-19. El Centro de Ciencia e Ingeniería de Sistemas (CSSE) de la Universidad Johns Hopkins (JHU); Los datos preprocesados ​​están aquí: Proyecto World in Data.
39. Paxson, Wei; Shen, Bo-Wen (1 de octubre de 2022). "Una ecuación KdV-SIR y sus soluciones analíticas para ondas epidémicas solitarias". Revista Internacional de Bifurcación y Caos . 32 (13): 2250199–2250780. Código Bib : 2022IJBC...3250199P. doi :10.1142/S0218127422501991. ISSN  0218-1274. S2CID  253314121.
40. Gao S, Teng Z, Nieto JJ, Torres A (2007). "Análisis de un modelo epidémico SIR con vacunación por pulsos y retardo distribuido". Revista de Biomedicina y Biotecnología . 2007 : 64870. doi : 10.1155/2007/64870 . PMC 2217597 . PMID  18322563. 
41. Brauer F, Castillo-Chávez C (2001). Modelos matemáticos en biología y epidemiología de poblaciones . Nueva York: Springer. ISBN 0-387-98902-1.
42. Para obtener más información sobre este tipo de modelo, consulte Anderson RM , ed. (mil novecientos ochenta y dos). Dinámica poblacional de enfermedades infecciosas: teoría y aplicaciones . Londres-Nueva York: Chapman y Hall. ISBN 0-412-21610-8.
43. Tembine, H (2020). "COVID-19: perspectiva de juego de tipo campo medio basada en datos". Diario de juegos . 11, 51 (4): 1–111 . Consultado el 24 de noviembre de 2022 .
44. Bartlett MS (1957). "Periodicidad del sarampión y tamaño de la comunidad". Revista de la Royal Statistical Society, Serie A. 120 (1): 48–70. doi :10.2307/2342553. JSTOR  2342553. S2CID  91114210.
45. Mayo RM, Lloyd AL (diciembre de 2001). "Dinámica de infección en redes sin escala". Revisión física E. 64 (6 parte 2): 066112. Código bibliográfico : 2001PhRvE..64f6112M. doi : 10.1103/PhysRevE.64.066112. PMID  11736241.
46. Pastor-Satorras R, Vespignani A (abril de 2001). "La epidemia se propaga en redes sin escala". Cartas de revisión física . 86 (14): 3200–3203. arXiv : cond-mat/0010317 . Código bibliográfico : 2001PhRvL..86.3200P. doi : 10.1103/PhysRevLett.86.3200. hdl :2117/126209. PMID  11290142. S2CID  16298768.
47. Newman ME (julio de 2002). "Propagación de enfermedades epidémicas en las redes". Revisión física E. 66 (1 parte 2): 016128. arXiv : cond-mat/0205009 . Código bibliográfico : 2002PhRvE..66a6128N. doi : 10.1103/PhysRevE.66.016128. PMID  12241447. S2CID  15291065.
48. Wong F, Collins JJ (noviembre de 2020). "La evidencia de que la superpropagación del coronavirus tiene cola gruesa". Actas de la Academia Nacional de Ciencias de los Estados Unidos de América . 117 (47): 29416–29418. Código Bib : 2020PNAS..11729416W. doi : 10.1073/pnas.2018490117 . PMC 7703634 . PMID  33139561. S2CID  226242440. 

Otras lecturas

• Mayo RM , Anderson RM (1991). Enfermedades infecciosas del ser humano: dinámica y control . Oxford: Prensa de la Universidad de Oxford. ISBN 0-19-854040-X.
• Vynnycky E, White RG, eds. (2010). Introducción al modelado de enfermedades infecciosas . Oxford: Prensa de la Universidad de Oxford. ISBN 978-0-19-856576-5.
• Capasso V (2008). Estructuras matemáticas de sistemas epidémicos. 2da Imprenta . Heidelberg: Springer. ISBN 978-3-540-56526-0.
• Carlson CS, Rubin DM, Heikkilä V, Postema M (2021). "Extracción de parámetros de transmisión y recuperación para un modelo adaptativo de dinámica de sistema global de la pandemia de COVID-19". IEEE África 2021 (PDF) . págs. 456–459. doi :10.1109/AFRICON51333.2021.9570946. ISBN 978-1-6654-1984-0. S2CID  239899862.

enlaces externos

• Modelo SIR: experimentos en línea con JSXGraph
• "Simulando una epidemia". 3Azul1Marrón . 27 de marzo de 2020 - vía YouTube .