Química cuántica relativista

Teorías de la química cuántica explicadas a través de la mecánica relativista

La química cuántica relativista combina la mecánica relativista con la química cuántica para calcular las propiedades y la estructura de los elementos , especialmente de los elementos más pesados ​​de la tabla periódica . Un ejemplo destacado es la explicación del color del oro : debido a los efectos relativistas, no es plateado como la mayoría de los demás metales. ^[1]

El término efectos relativistas se desarrolló a la luz de la historia de la mecánica cuántica. Inicialmente, la mecánica cuántica se desarrolló sin considerar la teoría de la relatividad . ^[2] Los efectos relativistas son aquellas discrepancias entre los valores calculados por modelos que consideran la relatividad y los que no. ^[3] Los efectos relativistas son importantes para elementos más pesados ​​con números atómicos altos , como los lantánidos y los actínidos . ^[4]

Los efectos relativistas en química pueden considerarse perturbaciones o pequeñas correcciones a la teoría no relativista de la química, que se desarrolla a partir de las soluciones de la ecuación de Schrödinger . Estas correcciones afectan a los electrones de manera diferente según la velocidad del electrón en comparación con la velocidad de la luz . Los efectos relativistas son más prominentes en los elementos pesados ​​porque solo en estos elementos los electrones alcanzan velocidades suficientes para que los elementos tengan propiedades que difieren de lo que predice la química no relativista. ^[5]

Historia

A partir de 1935, Bertha Swirles describió un tratamiento relativista de un sistema de muchos electrones, ^[6] a pesar de la afirmación de Paul Dirac de 1929 de que las únicas imperfecciones que quedan en la mecánica cuántica "dan lugar a dificultades solo cuando están involucradas partículas de alta velocidad y, por lo tanto, no tienen importancia en la consideración de la estructura atómica y molecular y las reacciones químicas ordinarias en las que, de hecho, generalmente es suficientemente preciso si uno descuida la variación de la relatividad de la masa y la velocidad y asume solo fuerzas de Coulomb entre los diversos electrones y núcleos atómicos". ^[7]

Los químicos teóricos en general estuvieron de acuerdo con el sentimiento de Dirac hasta la década de 1970, cuando se observaron efectos relativistas en elementos pesados. ^[8] La ecuación de Schrödinger había sido desarrollada sin considerar la relatividad en el artículo de Schrödinger de 1926. ^[9] Se hicieron correcciones relativistas a la ecuación de Schrödinger (ver ecuación de Klein-Gordon ) para describir la estructura fina de los espectros atómicos, pero este desarrollo y otros no se filtraron inmediatamente en la comunidad química. Dado que las líneas espectrales atómicas estaban en gran parte en el ámbito de la física y no en el de la química, la mayoría de los químicos no estaban familiarizados con la mecánica cuántica relativista, y su atención se centró en elementos más ligeros típicos del enfoque de la química orgánica de la época. ^[10]

La opinión de Dirac sobre el papel que desempeñaría la mecánica cuántica relativista en los sistemas químicos es errónea por dos razones. En primer lugar, los electrones en los orbitales atómicos s y p viajan a una fracción significativa de la velocidad de la luz. En segundo lugar, los efectos relativistas dan lugar a consecuencias indirectas que son especialmente evidentes para los orbitales atómicos d y f . ^[8]

Tratamiento cualitativo

Factor de Lorentz relativista (γ) en función de la velocidad. Para una velocidad pequeña, la (ordenada) es igual a pero como , tiende a infinito. ${\displaystyle E_{\text{rel}}}$ ${\displaystyle E_{0}=mc^{2},}$ ${\displaystyle v_{\text{e}}\to c}$ ${\displaystyle E_{\text{rel}}}$

Uno de los resultados más importantes y conocidos de la relatividad es que la masa relativista del electrón aumenta a medida que

$${\displaystyle m_{\text{rel}}={\frac {m_{\text{e}}}{\sqrt {1-(v_{\text{e}}/c)^{2}}}},}$$

donde son la masa en reposo del electrón , la velocidad del electrón y la velocidad de la luz respectivamente. La figura de la derecha ilustra este efecto relativista en función de la velocidad. ${\displaystyle m_{e},v_{e},c}$

Esto tiene una implicación inmediata en el radio de Bohr ( ), que viene dado por ${\displaystyle a_{0}}$

$${\displaystyle a_{0}={\frac {\hbar }{m_{\text{e}}c\alpha }},}$$

donde es la constante de Planck reducida , y α es la constante de estructura fina (una corrección relativista para el modelo de Bohr ). ${\displaystyle \hbar }$

Bohr calculó que un electrón orbital 1s de un átomo de hidrógeno que orbita en el radio de Bohr de 0,0529 nm viaja a casi 1/137 de la velocidad de la luz. ^[11] Se puede extender esto a un elemento más grande con un número atómico Z usando la expresión para un electrón 1s, donde v es su velocidad radial , es decir, su velocidad instantánea tangente al radio del átomo. Para el oro con Z  = 79, v  ≈ 0,58 c , por lo que el electrón 1s se moverá al 58% de la velocidad de la luz. Sustituyendo esto por v / c en la ecuación para la masa relativista, se encuentra que m _rel  = 1,22 m _e , y a su vez poniendo esto para el radio de Bohr anterior se encuentra que el radio se contrae en un 22%. ${\displaystyle v\approx {\frac {Zc}{137}}}$

Si se sustituye la "masa relativista" en la ecuación del radio de Bohr, se puede escribir $${\displaystyle a_{\text{rel}}={\frac {\hbar {\sqrt {1-(v_{\text{e}}/c)^{2}}}}{m_{\text{e}}c\alpha }}.}$$

Relación de los radios de Bohr relativistas y no relativistas, en función de la velocidad del electrón

Resulta que $${\displaystyle {\frac {a_{\text{rel}}}{a_{0}}}={\sqrt {1-(v_{\text{e}}/c)^{2}}}.}$$

A la derecha, se ha representado gráficamente la relación anterior entre los radios de Bohr relativistas y no relativistas en función de la velocidad del electrón. Observe cómo el modelo relativista muestra que el radio disminuye a medida que aumenta la velocidad.

Cuando el tratamiento de Bohr se extiende a átomos de hidrógeno , el radio de Bohr se convierte en donde es el número cuántico principal y Z es un entero para el número atómico . En el modelo de Bohr , el momento angular se da como . Sustituyendo en la ecuación anterior y resolviendo para se obtiene $${\displaystyle r={\frac {n^{2}}{Z}}a_{0}={\frac {n^{2}\hbar ^{2}4\pi \varepsilon _{0}}{m_{\text{e}}Ze^{2}}},}$$ ${\displaystyle n}$ ${\displaystyle mv_{\text{e}}r=n\hbar }$ ${\displaystyle v_{\text{e}}}$ $${\displaystyle {\begin{aligned}r&={\frac {n^{2}a_{0}}{Z}}={\frac {n\hbar }{mv_{\text{e}}}},\\v_{\text{e}}&={\frac {Z}{n^{2}a_{0}}}{\frac {n\hbar }{m}},\\{\frac {v_{\text{e}}}{c}}&={\frac {Z\alpha }{n}}={\frac {Ze^{2}}{4\pi \varepsilon _{0}\hbar cn}}.\end{aligned}}}$$

A partir de este punto, se pueden utilizar unidades atómicas para simplificar la expresión en; $${\displaystyle v_{\text{e}}={\frac {Z}{n}}.}$$

Sustituyendo esto en la expresión de la relación de Bohr mencionada anteriormente se obtiene $${\displaystyle {\frac {a_{\text{rel}}}{a_{0}}}={\sqrt {1-\left({\frac {Z}{nc}}\right)^{2}}}.}$$

En este punto, se puede ver que un valor bajo de y un valor alto de dan como resultado . Esto encaja con la intuición: los electrones con números cuánticos principales más bajos tendrán una mayor densidad de probabilidad de estar más cerca del núcleo. Un núcleo con una carga grande hará que un electrón tenga una alta velocidad. Una mayor velocidad del electrón significa una mayor masa relativista del electrón y, como resultado, los electrones estarán cerca del núcleo más tiempo y, por lo tanto, contraerán el radio para números cuánticos principales pequeños. ^[12] ${\displaystyle n}$ ${\displaystyle Z}$ ${\displaystyle {\frac {a_{\text{rel}}}{a_{0}}}<1}$

Desviaciones de la tabla periódica

Mercurio

El mercurio (Hg) es líquido hasta aproximadamente -39  °C , su punto de fusión . Las fuerzas de enlace son más débiles para los enlaces Hg-Hg que para sus vecinos inmediatos, como el cadmio (pf 321 °C) y el oro (pf 1064 °C). La contracción de los lantánidos solo explica parcialmente esta anomalía. ^{[11] Debido a que el} orbital 6s ² está contraído por efectos relativistas y, por lo tanto, puede contribuir solo débilmente a cualquier enlace químico, el enlace Hg-Hg debe ser principalmente el resultado de las fuerzas de van der Waals . ^{[11] [13] [14]}

El gas mercurio es en su mayor parte monoatómico, Hg(g). El Hg ₂ (g) se forma raramente y tiene una energía de disociación baja, como se esperaba debido a la falta de enlaces fuertes. ^[15]

Au ₂ (g) y Hg(g) son análogos a H ₂ (g) y He(g) en lo que respecta a que tienen la misma naturaleza de diferencia. La contracción relativista del orbital 6s ² hace que a veces se haga referencia al mercurio gaseoso como un pseudogas noble . ^[11]

Color del oro y del cesio

Curvas de reflectancia espectral para espejos metálicos de aluminio (Al), plata (Ag) y oro (Au)

Coloración de metales alcalinos: rubidio (plateado) versus cesio (dorado)

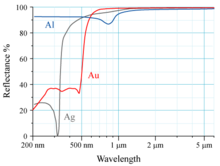
La reflectividad del aluminio (Al), la plata (Ag) y el oro (Au) se muestra en el gráfico de la derecha. El ojo humano percibe la radiación electromagnética con una longitud de onda cercana a los 600 nm como amarilla. El oro absorbe la luz azul más que otras longitudes de onda de luz visible; por lo tanto, la luz reflejada que llega al ojo carece de azul en comparación con la luz incidente. Como el amarillo es complementario del azul, esto hace que un trozo de oro bajo la luz blanca parezca amarillo a los ojos humanos.

La transición electrónica del orbital 5d al orbital 6s es responsable de esta absorción. Una transición análoga ocurre en la plata, pero los efectos relativistas son menores que en el oro. Mientras que el orbital 4d de la plata experimenta cierta expansión relativista y la contracción del orbital 5s, la distancia 4d-5s en la plata es mucho mayor que la distancia 5d-6s en el oro. Los efectos relativistas aumentan la distancia del orbital 5d al núcleo del átomo y disminuyen la distancia del orbital 6s. Debido a la disminución de la distancia orbital 6s, la transición electrónica absorbe principalmente en la región violeta/azul del espectro visible, a diferencia de la región UV. ^[16]

El cesio , el más pesado de los metales alcalinos que se puede recolectar en cantidades suficientes para su observación, tiene un tono dorado, mientras que los otros metales alcalinos son de color blanco plateado. Sin embargo, los efectos relativistas no son muy significativos en Z = 55 para el cesio (no muy lejos de Z = 47 para la plata). El color dorado del cesio proviene de la frecuencia decreciente de la luz requerida para excitar los electrones de los metales alcalinos a medida que el grupo desciende. Para el litio hasta el rubidio, esta frecuencia está en el ultravioleta, pero para el cesio alcanza el extremo azul-violeta del espectro visible; en otras palabras, la frecuencia plasmónica de los metales alcalinos se vuelve más baja desde el litio hasta el cesio. Por lo tanto, el cesio transmite y absorbe parcialmente la luz violeta preferentemente, mientras que otros colores (que tienen una frecuencia más baja) se reflejan; por lo tanto, parece amarillento. ^[17]

Batería de plomo-ácido

Sin la relatividad, se esperaría que el plomo ( Z = 82) se comportara de forma muy similar al estaño ( Z = 50), por lo que las baterías de estaño-ácido deberían funcionar tan bien como las baterías de plomo-ácido que se usan comúnmente en los automóviles. Sin embargo, los cálculos muestran que aproximadamente 10 V de los 12 V producidos por una batería de plomo-ácido de 6 celdas surgen puramente de efectos relativistas, lo que explica por qué las baterías de estaño-ácido no funcionan. ^[18]

Efecto de par inerte

En los complejos de Tl(I) ( talio ), Pb(II) ( plomo ) y Bi(III) ( bismuto ) existe un par de electrones 6s ^{2 . El efecto del par inerte es la tendencia de este par de electrones a resistir} la oxidación debido a una contracción relativista del orbital 6s. ^[8]

Otros efectos

Otros fenómenos comúnmente causados ​​por efectos relativistas son los siguientes:

• El efecto de los efectos relativistas sobre las interacciones metalófilas es incierto. Aunque Runeberg et al. (1999) calcularon un efecto atractivo, ^[19] Wan et al. (2021) calcularon en cambio un efecto repulsivo. ^[20]
• La estabilidad de los aniones de oro y platino en compuestos como el aururo de cesio . ^[21]
• La reactividad ligeramente reducida del francio en comparación con el cesio. ^{[22] [23]}
• Aproximadamente el 10% de la contracción de los lantánidos se atribuye a la masa relativista de los electrones de alta velocidad y al radio de Bohr más pequeño resultante. ^[24]

Véase también

• Energía de ionización
• Electronegatividad
• Afinidad electrónica
• Mecánica cuántica
• Mecánica cuántica relativista

Referencias

1. Pekka Pyykkö (enero de 2012). "Efectos relativistas en química: más comunes de lo que se pensaba". Revista anual de química física . 63 (1): 45–64. Bibcode :2012ARPC...63...45P. doi :10.1146/annurev-physchem-032511-143755. PMID  22404585.
2. Kleppner, Daniel (1999). "Una breve historia de la física atómica en el siglo XX" (PDF) . Reseñas de Física Moderna . 71 (2): S78–S84. Código Bibliográfico :1999RvMPS..71...78K. doi :10.1103/RevModPhys.71.S78. Archivado desde el original (PDF) el 2016-03-03 . Consultado el 2012-07-17 .
3. Kaldor, U.; Wilson, Stephen (2003). Química teórica y física de elementos pesados ​​y superpesados. Dordrecht, Países Bajos: Kluwer Academic Publishers. pág. 4. ISBN 978-1-4020-1371-3.
4. Kaldor, U.; Wilson, Stephen (2003). Química teórica y física de elementos pesados ​​y superpesados. Dordrecht, Países Bajos: Kluwer Academic Publishers. p. 2. ISBN 978-1-4020-1371-3.
5. Gupta, VP (22 de octubre de 2015). Principios y aplicaciones de la química cuántica. Elsevier Science. ISBN 978-0-12-803478-1. Recuperado el 7 de enero de 2024 .
6. Swirles, B. (1935). "El campo relativista autoconsistente". Actas de la Royal Society A: Ciencias matemáticas, físicas e ingeniería . 152 (877): 625–649. Bibcode :1935RSPSA.152..625S. doi : 10.1098/rspa.1935.0211 .
7. Dirac, PAM (1929). "Mecánica cuántica de sistemas de muchos electrones". Actas de la Royal Society A: Ciencias matemáticas, físicas e ingeniería . 123 (792): 714–733. Bibcode :1929RSPSA.123..714D. doi : 10.1098/rspa.1929.0094 . JSTOR  95222.
8. Pyykkö, Pekka (1988). "Efectos relativistas en la química estructural". Chemical Reviews . 88 (3): 563–594. doi :10.1021/cr00085a006.
9. Erwin Schrödinger (1926). "Über das Verhältnis der Heisenberg-Born-Jordanschen Quantenmechanik zu der meinem" (PDF) . Annalen der Physik (en alemán). 384 (8). Leipzig: 734–756. Código bibliográfico : 1926AnP...384..734S. doi : 10.1002/andp.19263840804. Archivado desde el original (PDF) el 17 de diciembre de 2008.
10. Kaldor, U.; Wilson, Stephen, eds. (2003). Química teórica y física de elementos pesados ​​y superpesados. Dordrecht, Países Bajos: Kluwer Academic Publishers. p. 17. ISBN 978-1-4020-1371-3.
11. Norrby, Lars J. (1991). "¿Por qué el mercurio es líquido? O, ¿por qué los efectos relativistas no se incluyen en los libros de texto de química?". Journal of Chemical Education . 68 (2): 110. Bibcode :1991JChEd..68..110N. doi :10.1021/ed068p110.
12. Pitzer, Kenneth S. (1979). "Efectos relativistas sobre las propiedades químicas" (PDF) . Accounts of Chemical Research . 12 (8): 271–276. doi :10.1021/ar50140a001. S2CID  95601322.
13. Calvo, Florent; Pahl, Elke; Gusano, Michael; Schwerdtfeger, Peter (2013). "Evidencia del derretimiento del mercurio a baja temperatura debido a la relatividad". Edición internacional Angewandte Chemie . 52 (29): 7583–7585. doi :10.1002/anie.201302742. ISSN  1521-3773. PMID  23780699.
14. Howes2013-06-21T00:00:00+01:00, Laura. "La relatividad detrás de la liquidez del mercurio". Chemistry World . Consultado el 21 de enero de 2022 .{{cite web}}: CS1 maint: numeric names: authors list (link)
15. Zehnacker, A (1 de junio de 1987). "Estudio experimental del dímero de mercurio frío". Journal of Chemical Physics . 86 (11): 6565–6566. Código Bibliográfico :1987JChPh..86.6565Z. doi :10.1063/1.452401.
16. Pyykkö, Pekka; Desclaux, Jean Paul (1979). "Relatividad y el sistema periódico de elementos". Accounts of Chemical Research . 12 (8): 276. doi :10.1021/ar50140a002.
17. Addison, CC (1984). La química de los metales alcalinos líquidos . Wiley. pág. 7. ISBN 9780471905080.
18. Ahuja, Rajeev; Blomqvist, Anders; Larsson, Peter; Pyykkö, Pekka; Zaleski-Ejgierd, Patryk (2011). "Relatividad y la batería de plomo-ácido". Physical Review Letters . 106 (1): 018301. arXiv : 1008.4872 . Código Bibliográfico :2011PhRvL.106a8301A. doi :10.1103/PhysRevLett.106.018301. PMID  21231773. S2CID  39265906.
19. Runeberg, Nino; Schütz, Martin; Werner, Hans-Joachim (1999). "La atracción aurofílica según la interpretación de los métodos de correlación local". J. Chem. Phys. 110 (15): 7210–7215. Bibcode :1999JChPh.110.7210R. doi :10.1063/1.478665.
20. Wan, Qingyun; Yang, Jun; To, Wai-Pong; Che, Chi-Ming (5 de enero de 2021). "La fuerte repulsión de Pauli metal-metal conduce a una metalofilia repulsiva en complejos organometálicos de capa cerrada d 8 y d 10". Actas de la Academia Nacional de Ciencias . 118 (1): e2019265118. Bibcode :2021PNAS..11819265W. doi : 10.1073/pnas.2019265118 . ISSN  0027-8424. PMC 7817198 . PMID  33372160. 
21. Jansen, Martin (diciembre de 2005). "Efectos del movimiento relativista de los electrones en la química del oro y el platino". Solid State Sciences . 7 (12): 1464–1474. Bibcode :2005SSSci...7.1464J. doi : 10.1016/j.solidstatesciences.2005.06.015 .
22. "Elementos 087 del IYPT 2019: Francio: no es el elemento del grupo 1 más reactivo". Exploraciones de compuestos químicos cotidianos . 6 de noviembre de 2019.
23. Andreev, SV; Letokhov, VS; Mishin, VI (21 de septiembre de 1987). "Espectroscopia de fotoionización por resonancia láser de niveles de Rydberg en Fr". Physical Review Letters . 59 (12): 1274–1276. Bibcode :1987PhRvL..59.1274A. doi :10.1103/PhysRevLett.59.1274. PMID  10035190.
24. Pyykko, Pekka (1 de mayo de 1988). "Efectos relativistas en la química estructural". Chemical Reviews . 88 (3): 563–594. doi :10.1021/cr00085a006.

Lectura adicional

• PA Christiansen; WC Ermler; KS Pitzer. Efectos relativistas en sistemas químicos. Revista anual de química física 1985 , 36 , 407–432. doi :10.1146/annurev.pc.36.100185.002203