Problema de maximización de utilidad

Problema de la asignación del dinero por parte de los consumidores para obtener el mayor beneficio posible

La maximización de la utilidad fue desarrollada por primera vez por los filósofos utilitaristas Jeremy Bentham y John Stuart Mill . En microeconomía , el problema de maximización de la utilidad es el problema al que se enfrentan los consumidores : "¿Cómo debo gastar mi dinero para maximizar mi utilidad ?". Es un tipo de problema de decisión óptima . Consiste en elegir qué cantidad de cada bien o servicio disponible consumir, teniendo en cuenta una restricción sobre el gasto total (renta), los precios de los bienes y sus preferencias .

La maximización de la utilidad es un concepto importante en la teoría del consumidor, ya que muestra cómo los consumidores deciden asignar sus ingresos. Debido a que los consumidores están modelados como racionales , buscan extraer el mayor beneficio para sí mismos. Sin embargo, debido a la racionalidad limitada y otros sesgos, los consumidores a veces eligen paquetes que no necesariamente maximizan su utilidad. El paquete de maximización de la utilidad del consumidor tampoco es fijo y puede cambiar con el tiempo dependiendo de sus preferencias individuales de bienes, cambios de precios y aumentos o disminuciones en los ingresos.

Configuración básica

Para maximizar la utilidad hay un proceso de cuatro pasos básicos para derivar la demanda del consumidor y encontrar el paquete que maximiza la utilidad del consumidor dados los precios, ingresos y preferencias.

1) Verificar si se cumple la ley de Walras 2) 'Bang for buck' 3) la restricción presupuestaria 4) Verificar la negatividad

1) Ley de Walras

La ley de Walras establece que si las preferencias de un consumidor son completas, monótonas y transitivas, entonces la demanda óptima estará en la línea presupuestaria . ^[1]

Preferencias del consumidor

Para que exista una representación de utilidad las preferencias del consumidor deben ser completas y transitivas (condiciones necesarias). ^[2]

Completo

La completitud de las preferencias indica que el consumidor puede comparar todos los paquetes del conjunto de consumo. Por ejemplo, si el consumidor tiene tres paquetes A, B y C, entonces:

A B, A C, B A, B C, C B, C A, A A, B B, C C. Por lo tanto, el consumidor tiene preferencias completas ya que puede comparar cada paquete. ${\displaystyle \succcurlyeq }$ ${\displaystyle \succcurlyeq }$ ${\displaystyle \succcurlyeq }$ ${\displaystyle \succcurlyeq }$ ${\displaystyle \succcurlyeq }$ ${\displaystyle \succcurlyeq }$ ${\displaystyle \succcurlyeq }$ ${\displaystyle \succcurlyeq }$ ${\displaystyle \succcurlyeq }$

Transitivo

La transitividad establece que las preferencias de los individuos son consistentes en todos los paquetes.

Por lo tanto, si el consumidor prefiere débilmente A sobre B (A B) y B C esto significa que A C (A es débilmente preferido a C) ${\displaystyle \succcurlyeq }$ ${\displaystyle \succcurlyeq }$ ${\displaystyle \succcurlyeq }$

Monótono

Para que una relación de preferencia sea monótona, aumentar la cantidad de ambos bienes debería mejorar estrictamente la situación del consumidor (aumentar su utilidad), y aumentar la cantidad de un bien manteniendo constante la del otro no debería empeorar la situación del consumidor (misma utilidad).

La preferencia es monótona si y sólo si; ${\displaystyle \succcurlyeq }$

1) ${\displaystyle (x+\epsilon ,y)\succcurlyeq (x,y)}$

2) ${\displaystyle (x,y+\epsilon )\succcurlyeq (x,y)}$

3) ${\displaystyle (x+\epsilon ,y+\epsilon )\succ (x,y)}$

donde > 0 ${\displaystyle \epsilon }$

2) 'Buena relación calidad-precio'

El concepto de "bang for buck" (beneficio por dólar) se refiere al deseo del consumidor de obtener el mejor valor por su dinero. Si se cumple la ley de Walras, la solución óptima del consumidor se encuentra en el punto donde se cruzan la línea presupuestaria y la curva de indiferencia óptima; esto se denomina condición de tangencia. ^[3] Para encontrar este punto, se diferencia la función de utilidad con respecto a x e y para hallar las utilidades marginales, y luego se divide por los respectivos precios de los bienes.

${\displaystyle MU_{x}/p_{x}=MU_{y}/p_{y}}$

Esto se puede resolver para encontrar la cantidad óptima del bien x o del bien y.

3) Restricción presupuestaria

La configuración básica de la restricción presupuestaria del consumidor es: ${\displaystyle p_{x}x+p_{y}y\leq I}$

Debido a que se cumple la ley de Walras: ${\displaystyle p_{x}x+p_{y}y=I}$

Luego se sustituye la condición de tangencia para hallar la cantidad óptima del otro bien.

4) Compruebe la negatividad

Figura 1: Esto representa dónde se encuentra el paquete que maximiza la utilidad cuando la demanda de un bien es negativa.

Se debe comprobar la negatividad, ya que el problema de maximización de la utilidad puede dar una respuesta en la que la demanda óptima de un bien es negativa, lo que en realidad no es posible porque está fuera del dominio. Si la demanda de un bien es negativa, la cesta de consumo óptima será aquella en la que no se consume ningún bien de ese bien y todos los ingresos se gastan en el otro bien (una solución de esquina). Véase la figura 1 para ver un ejemplo en el que la demanda del bien x es negativa.

Una representación técnica

Supongamos que el conjunto de consumo del consumidor es , o la enumeración de todos los posibles paquetes de consumo que podrían seleccionarse si hubiera una restricción presupuestaria.

El conjunto de consumo = (un conjunto de números reales positivos, el consumidor no puede preferir una cantidad negativa de bienes). ${\displaystyle \mathbb {R} _{+}^{n}\ .}$

${\displaystyle x\in \mathbb {R} _{+}^{n}\ .}$

Supongamos también que el vector de precios ( p ) de los n productos es positivo,

Figura 2: Muestra las cantidades óptimas de bienes x e y que maximizan la utilidad dada una restricción presupuestaria.

${\displaystyle p\in \mathbb {R} _{+}^{n}\ ,}$

y que el ingreso del consumidor es ; entonces el conjunto de todos los paquetes asequibles, el conjunto presupuestario es, ${\displaystyle I}$

${\displaystyle B(p,I)=\{x\in \mathbb {R} _{+}^{n}|\mathbb {\Sigma } _{i=1}^{n}p_{i}x_{i}\leq I\}\ ,}$

Al consumidor le gustaría comprar el mejor paquete de productos asequible.

Se supone que el consumidor tiene una función de utilidad ordinal , denominada u . Es una función de valor real cuyo dominio es el conjunto de todos los paquetes de productos, o

${\displaystyle u:\mathbb {R} _{+}^{n}\rightarrow \mathbb {R} _{+}\ .}$

Entonces, la elección óptima del consumidor es el paquete que maximiza la utilidad de todos los paquetes en el conjunto presupuestario, si entonces la función de demanda óptima del consumidor es: ${\displaystyle x(p,I)}$ ${\displaystyle x\in B(p,I)}$

${\displaystyle x(p,I)=\{x\in B(p,I)|U(x)\geq U(y)\forall y\in B(p,I)\}}$

Encontrar es el problema de maximización de la utilidad . ${\displaystyle x(p,I)}$

Si u es continua y ningún bien es gratuito, entonces existe ^[4] , pero no es necesariamente única. Si las preferencias del consumidor son completas, transitivas y estrictamente convexas, entonces la demanda del consumidor contiene un maximizador único para todos los valores de los parámetros precio y riqueza. Si esto se satisface, entonces se denomina función de demanda marshalliana . De lo contrario, tiene un valor fijo y se denomina correspondencia de demanda marshalliana . ${\displaystyle x(p,I)}$ ${\displaystyle x(p,I)}$ ${\displaystyle x(p,I)}$

Maximización de la utilidad de los complementos perfectos

U = mín {x, y}

Figura 3: Esto muestra el problema de maximización de utilidad con una función de utilidad mínima.

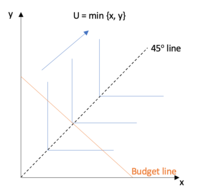
Para una función mínima con bienes que son complementos perfectos , no se pueden seguir los mismos pasos para encontrar la cesta que maximiza la utilidad, ya que es una función no diferenciable. Por lo tanto, se debe utilizar la intuición. El consumidor maximizará su utilidad en el punto de inflexión de la curva de indiferencia más alta que interseca la línea presupuestaria donde x = y. ^[3] Esto es intuición, ya que como el consumidor es racional, no tiene sentido que el consumidor consuma más de un bien y no del otro, ya que su utilidad se toma en el mínimo de los dos (no obtiene ninguna ganancia en utilidad de esto y estaría desperdiciando sus ingresos). Véase la figura 3.

Maximización de la utilidad de sustitutos perfectos

U = x + y

En el caso de una función de utilidad con sustitutos perfectos , la cesta que maximiza la utilidad se puede hallar por diferenciación o simplemente por inspección. Supongamos que un consumidor considera que escuchar a las bandas de rock australianas AC/DC y Tame Impala son sustitutos perfectos. Esto significa que está contento de pasar toda la tarde escuchando sólo a AC/DC, o sólo a Tame Impala, o tres cuartos de AC/DC y un cuarto de Tame Impala, o cualquier combinación de las dos bandas en cualquier cantidad. Por tanto, la elección óptima del consumidor está determinada enteramente por los precios relativos de escuchar a los dos artistas. Si asistir a un concierto de Tame Impala es más barato que asistir al concierto de AC/DC, el consumidor elige asistir al concierto de Tame Impala, y viceversa. Si los precios de los dos conciertos son iguales, el consumidor es completamente indiferente y puede lanzar una moneda para decidir. Para ver esto matemáticamente, desmarque la función de utilidad para ver que la TMS es constante: este es el significado técnico de los sustitutos perfectos. Como resultado de esto, la solución al problema de maximización restringida del consumidor no será (por lo general) una solución interior y, por lo tanto, se debe verificar el nivel de utilidad en los casos límite (gastar todo el presupuesto en el bien x, gastar todo el presupuesto en el bien y) para ver cuál es la solución. El caso especial es cuando la TMS (constante) es igual a la relación de precios (por ejemplo, ambos bienes tienen el mismo precio y los mismos coeficientes en la función de utilidad). En este caso, cualquier combinación de los dos bienes es una solución al problema del consumidor.

Reacción a los cambios de precios

Para un nivel dado de riqueza real, a los consumidores sólo les importan los precios relativos, no los precios absolutos. Si los consumidores reaccionaran a los cambios en los precios nominales y la riqueza nominal incluso si los precios relativos y la riqueza real permanecieran invariables, esto sería un efecto llamado ilusión monetaria . Las condiciones matemáticas de primer orden para un máximo del problema del consumidor garantizan que la demanda de cada bien sea homogénea de grado cero conjuntamente en precios nominales y riqueza nominal, por lo que no hay ilusión monetaria.

Cuando los precios de los bienes cambian, el consumo óptimo de estos bienes dependerá de los efectos de la sustitución y del ingreso. El efecto de la sustitución dice que si la demanda de ambos bienes es homogénea, cuando el precio de un bien disminuye (manteniendo constante el precio del otro bien), el consumidor consumirá más de este bien y menos del otro, ya que se vuelve relativamente más barato. Lo mismo sucede si el precio de un bien aumenta, los consumidores comprarán menos de ese bien y más del otro. ^[5]

El efecto renta se produce cuando el cambio de precio de un bien provoca un cambio en la renta. Si el precio de un bien aumenta, la renta disminuye (es más costoso que antes consumir el mismo paquete), lo mismo ocurre si el precio de un bien baja, la renta aumenta (es más barato consumir el mismo paquete, por lo que se puede consumir más de la combinación deseada de bienes). ^[5]

Reacción a los cambios en los ingresos

Figura 5: Muestra cómo cambia el paquete óptimo de un consumidor cuando aumenta su ingreso.

Si el ingreso de los consumidores aumenta, su línea presupuestaria se desplaza hacia afuera y ahora tienen más ingresos para gastar en el bien x, el bien y, o ambos, dependiendo de sus preferencias por cada bien. Si tanto los bienes x como y fueran bienes normales , entonces el consumo de ambos bienes aumentaría y la cesta óptima se movería de A a C (véase la figura 5). Si tanto x como y fueran bienes inferiores , entonces la demanda de estos disminuiría a medida que aumenta el ingreso (la cesta óptima estaría en el punto B o C). ^[6]

Racionalidad limitada

Para mayor información véase: Racionalidad limitada

En la práctica, un consumidor no siempre puede elegir un paquete óptimo. Por ejemplo, puede requerir demasiada reflexión o demasiado tiempo. La racionalidad limitada es una teoría que explica este comportamiento. Algunos ejemplos de alternativas a la maximización de la utilidad debido a la racionalidad limitada son: la satisfacción , la eliminación por aspectos y la heurística de contabilidad mental.

• La heurística de satisfacción es cuando un consumidor define un nivel de aspiración y busca hasta encontrar una opción que lo satisfaga; considerará que esta opción es suficientemente buena y dejará de buscar. ^[7]
• La eliminación por aspectos consiste en definir un nivel para cada aspecto de un producto que se desea y eliminar todas las demás opciones que no cumplen este requisito, por ejemplo, precio inferior a 100 dólares, color, etc., hasta que solo quede un producto que se supone que será el producto que elegirá el consumidor. ^[8]
• La heurística de la contabilidad mental : en esta estrategia se observa que las personas suelen asignar valores subjetivos a su dinero en función de sus preferencias por distintas cosas. Una persona desarrollará cuentas mentales para distintos gastos, asignará su presupuesto dentro de ellas y luego intentará maximizar su utilidad dentro de cada cuenta. ^[9]

Conceptos relacionados

La relación entre la función de utilidad y la demanda marshalliana en el problema de maximización de la utilidad refleja la relación entre la función de gasto y la demanda hicksiana en el problema de minimización del gasto . En la minimización del gasto, el nivel de utilidad está dado, así como los precios de los bienes; el papel del consumidor es encontrar un nivel mínimo de gasto necesario para alcanzar este nivel de utilidad.

La regla de elección social utilitarista es una regla que dice que la sociedad debe elegir la alternativa que maximice la suma de utilidades. Mientras que la maximización de la utilidad la realizan los individuos, la maximización de la suma de utilidades la realiza la sociedad.

Véase también

• Maximización del bienestar
• Maximización de beneficios
• Modelado de elección
• Problema de minimización del gasto
• Decisión óptima
• Efecto sustitución
• Función de utilidad
• Ley de la demanda
• Utilidad marginal

Referencias

1. Levin, Jonothan (2004). Teoría del consumidor . Universidad de Stanford. Págs. 4-6.
2. Salcedo, Bruno (2017). Representaciones de utilidad . Universidad de Cornell. Págs. 18-19.
3. Board, Simon (2009). Problema de maximización de utilidad . Departamento de Economía, UCLA. pp. 10–17.
4. Elección, preferencia y utilidad . Princeton University Press. NDP 14.{{cite book}}: CS1 maint: year (link)
5. Maximización de la utilidad y demanda . Biblioteca de la Universidad de Minnesota. 2011. pp. capítulo 7.2.
6. Rice University (nd). "Cómo los cambios en los ingresos y los precios afectan las decisiones de consumo". Libros de prensa . Consultado el 22 de abril de 2021 .
7. Wheeler, Gregory (2018). Racionalidad limitada . Enciclopedia de filosofía de Stanford.
8. "Modelo de eliminación por aspectos". Universidad de Monash . 2018 . Consultado el 20 de abril de 2021 .
9. "¿Por qué pensamos menos en algunas compras que en otras?". The decision lab . 2021 . Consultado el 20 de abril de 2021 .

Enlaces externos

• Anatomía de las funciones de utilidad de tipo Cobb-Douglas en 3D
• Reglas para maximizar la utilidad mediante el aprendizaje del lumen
• Un ejemplo de maximización de la utilidad
• Definición de maximización de utilidad según la ayuda de Economía
• Aplicación de una función de utilidad por Investopedia
• Definición de bienes sustitutos según Investopedia