Teoría de la renovación

Rama de la teoría de la probabilidad

La teoría de la renovación es la rama de la teoría de la probabilidad que generaliza el proceso de Poisson para tiempos de tenencia arbitrarios. En lugar de tiempos de espera distribuidos exponencialmente , un proceso de renovación puede tener tiempos de espera independientes e idénticamente distribuidos (IID) que tengan una media finita. Un proceso de renovación de recompensas tiene además una secuencia aleatoria de recompensas obtenidas en cada tiempo de retención, que son IID pero no necesitan ser independientes de los tiempos de retención.

Un proceso de renovación tiene propiedades asintóticas análogas a la ley fuerte de los grandes números y al teorema del límite central . La función de renovación (número esperado de llegadas) y la función de recompensa (valor de recompensa esperado) son de importancia clave en la teoría de la renovación. La función de renovación satisface una ecuación integral recursiva, la ecuación de renovación. La ecuación de renovación clave proporciona el valor límite de la convolución de con una función no negativa adecuada. La superposición de procesos de renovación puede estudiarse como un caso especial de los procesos de renovación de Markov . ${\displaystyle m(t)}$ ${\displaystyle g(t)}$ ${\displaystyle m'(t)}$

Las aplicaciones incluyen calcular la mejor estrategia para reemplazar maquinaria desgastada en una fábrica y comparar los beneficios a largo plazo de diferentes pólizas de seguro. La paradoja de la inspección se relaciona con el hecho de que observar un intervalo de renovación en el tiempo t da un intervalo con un valor promedio mayor que el de un intervalo de renovación promedio.

Procesos de renovación

Introducción

El proceso de renovación es una generalización del proceso de Poisson . En esencia, el proceso de Poisson es un proceso de Markov de tiempo continuo en los números enteros positivos (generalmente comenzando en cero) que tiene tiempos de retención independientes distribuidos exponencialmente en cada número entero antes de avanzar al siguiente número entero . En un proceso de renovación, los tiempos de espera no necesitan tener una distribución exponencial; más bien, los tiempos de espera pueden tener cualquier distribución en los números positivos, siempre que los tiempos de espera sean independientes e idénticamente distribuidos ( IID ) y tengan una media finita. ${\displaystyle i}$ ${\displaystyle i+1}$

Definicion formal

Ejemplo de evolución de un proceso de renovación con _tiempos de retención _Si y tiempos de salto Jn .

Sea una secuencia de variables aleatorias independientes positivas distribuidas idénticamente con un valor esperado finito ${\displaystyle (S_{i})_{i\geq 1}}$

${\displaystyle 0<\operatorname {E} [S_{i}]<\infty .}$

Nos referimos a la variable aleatoria como el " ésimo tiempo de retención". ${\displaystyle S_{i}}$ ${\displaystyle i}$

Definir para cada n > 0 :

${\displaystyle J_{n}=\sum _{i=1}^{n}S_{i},}$

cada uno se denomina " ésimo tiempo de salto" y los intervalos se denominan "intervalos de renovación". ${\displaystyle J_{n}}$ ${\displaystyle n}$ ${\displaystyle [J_{n},J_{n+1}]}$

Entonces está dada por una variable aleatoria ${\displaystyle (X_{t})_{t\geq 0}}$

${\displaystyle X_{t}=\sum _{n=1}^{\infty }\operatorname {\mathbb {I} } _{\{J_{n}\leq t\}}=\sup \left\{\,n:J_{n}\leq t\,\right\}}$

¿Dónde está la función indicadora ? ${\displaystyle \operatorname {\mathbb {I} } _{\{J_{n}\leq t\}}}$

${\displaystyle \operatorname {\mathbb {I} } _{\{J_{n}\leq t\}}={\begin{cases}1,&{\text{if }}J_{n}\leq t\\0,&{\text{otherwise}}\end{cases}}}$

${\displaystyle (X_{t})_{t\geq 0}}$representa el número de saltos que se han producido en el tiempo t , y se denomina proceso de renovación.

Interpretación

Si se consideran eventos que ocurren en momentos aleatorios, se puede optar por pensar en los tiempos de espera como el tiempo aleatorio transcurrido entre dos eventos consecutivos. Por ejemplo, si el proceso de renovación modela el número de averías de diferentes máquinas, entonces el tiempo de espera representa el tiempo entre que una máquina se avería antes de que lo haga otra. ${\displaystyle \{S_{i}:i\geq 1\}}$

El proceso de Poisson es el proceso de renovación único con la propiedad de Markov , ^[1] ya que la distribución exponencial es la única variable aleatoria continua con la propiedad de falta de memoria.

Procesos de renovación-recompensa

_{Ejemplo de evolución de un proceso de} renovación-recompensa con tiempos de retención Si , tiempos de salto Jn y recompensas _{W i}

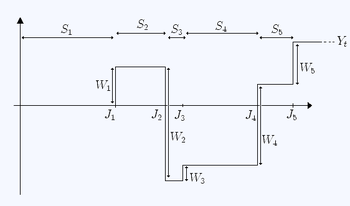
Sea una secuencia de variables aleatorias IID ( recompensas ) que satisfagan ${\displaystyle W_{1},W_{2},\ldots }$

${\displaystyle \operatorname {E} |W_{i}|<\infty .\,}$

Entonces la variable aleatoria

${\displaystyle Y_{t}=\sum _{i=1}^{X_{t}}W_{i}}$

Se llama proceso de renovación-recompensa . Tenga en cuenta que, a diferencia de , cada uno puede tomar valores negativos y positivos. ${\displaystyle S_{i}}$ ${\displaystyle W_{i}}$

La variable aleatoria depende de dos secuencias: los tiempos de espera y las recompensas. Estas dos secuencias no tienen por qué ser independientes. En particular, puede ser una función de . ${\displaystyle Y_{t}}$ ${\displaystyle S_{1},S_{2},\ldots }$ ${\displaystyle W_{1},W_{2},\ldots }$ ${\displaystyle W_{i}}$ ${\displaystyle S_{i}}$

Interpretación

En el contexto de la interpretación anterior de los tiempos de espera como el tiempo entre fallos sucesivos de una máquina, las "recompensas" (que en este caso son negativas) pueden considerarse como los costes de reparación sucesivos incurridos como resultado de las sucesivas mal funcionamiento. ${\displaystyle W_{1},W_{2},\ldots }$

Una analogía alternativa es que tenemos un ganso mágico que pone huevos a intervalos (tiempos de retención) distribuidos como . A veces pone huevos de oro de peso aleatorio y, a veces, huevos tóxicos (también de peso aleatorio) que requieren una eliminación responsable (y costosa). Las "recompensas" son las pérdidas/ganancias financieras sucesivas (aleatorias) resultantes de huevos sucesivos ( i = 1,2,3,...) y registran la "recompensa" financiera total en el momento t . ${\displaystyle S_{i}}$ ${\displaystyle W_{i}}$ ${\displaystyle Y_{t}}$

Función de renovación

Definimos la función de renovación como el valor esperado del número de saltos observados hasta cierto tiempo : ${\displaystyle t}$

${\displaystyle m(t)=\operatorname {E} [X_{t}].\,}$

Teorema de renovación elemental

La función de renovación satisface

${\displaystyle \lim _{t\to \infty }{\frac {1}{t}}m(t)={\frac {1}{\operatorname {E} [S_{1}]}}.}$

Teorema de renovación elemental para procesos de recompensa por renovación.

Definimos la función de recompensa :

${\displaystyle g(t)=\operatorname {E} [Y_{t}].\,}$

La función de recompensa satisface

${\displaystyle \lim _{t\to \infty }{\frac {1}{t}}g(t)={\frac {\operatorname {E} [W_{1}]}{\operatorname {E} [S_{1}]}}.}$

Ecuación de renovación

La función de renovación satisface

${\displaystyle m(t)=F_{S}(t)+\int _{0}^{t}m(t-s)f_{S}(s)\,ds}$

donde es la función de distribución acumulada de y es la función de densidad de probabilidad correspondiente. ${\displaystyle F_{S}}$ ${\displaystyle S_{1}}$ ${\displaystyle f_{S}}$

Teorema de renovación clave

Sea X un proceso de renovación con función de renovación y media de interrenovación . Sea una función que satisfaga: ${\displaystyle m(t)}$ ${\displaystyle \mu }$ ${\displaystyle g:[0,\infty )\rightarrow [0,\infty )}$

• ${\displaystyle \int _{0}^{\infty }g(t)\,dt<\infty }$
• g es monótono y no creciente

El teorema clave de la renovación establece que, como : ^[3] ${\displaystyle t\rightarrow \infty }$

${\displaystyle \int _{0}^{t}g(t-x)m'(x)\,dx\rightarrow {\frac {1}{\mu }}\int _{0}^{\infty }g(x)\,dx}$

Teorema de renovación

Considerando para cualquier caso especial el teorema de renovación: ^[4] ${\displaystyle g(x)=\mathbb {I} _{[0,h]}(x)}$ ${\displaystyle h>0}$

${\displaystyle m(t+h)-m(t)\rightarrow {\frac {h}{\mu }}}$como ${\displaystyle t\rightarrow \infty }$

El resultado se puede demostrar mediante ecuaciones integrales o mediante un argumento de acoplamiento . ^[5] Aunque es un caso especial del teorema de renovación clave, se puede utilizar para deducir el teorema completo, considerando funciones escalonadas y luego aumentando secuencias de funciones escalonadas. ^[3]

Propiedades asintóticas

Los procesos de renovación y los procesos de renovación-recompensa tienen propiedades análogas a la ley fuerte de los grandes números , que pueden derivarse del mismo teorema. Si es un proceso de renovación y es un proceso de renovación-recompensa entonces: ${\displaystyle (X_{t})_{t\geq 0}}$ ${\displaystyle (Y_{t})_{t\geq 0}}$

${\displaystyle \lim _{t\to \infty }{\frac {1}{t}}X_{t}={\frac {1}{\operatorname {E} [S_{1}]}}}$^[6]

${\displaystyle \lim _{t\to \infty }{\frac {1}{t}}Y_{t}={\frac {1}{\operatorname {E} [S_{1}]}}\operatorname {E} [W_{1}]}$

casi con seguridad.

Los procesos de renovación tienen además una propiedad análoga al teorema del límite central : ^[6]

${\displaystyle {\frac {X_{t}-t/\mu }{\sqrt {t\sigma ^{2}/\mu ^{3}}}}}$

Paradoja de la inspección

El intervalo de renovación determinado por el punto aleatorio t (que se muestra en rojo) es estocásticamente mayor que el primer intervalo de renovación.

Una característica curiosa de los procesos de renovación es que si esperamos un tiempo predeterminado t y luego observamos qué tan grande es el intervalo de renovación que contiene t , deberíamos esperar que sea típicamente mayor que un intervalo de renovación de tamaño promedio.

Matemáticamente, la paradoja de la inspección establece: para cualquier t > 0, el intervalo de renovación que contiene t es estocásticamente mayor que el primer intervalo de renovación. Es decir, para todo x > 0 y para todo t > 0:

${\displaystyle \operatorname {P} (S_{X_{t}+1}>x)\geq \operatorname {P} (S_{1}>x)=1-F_{S}(x)}$

donde F _S es la función de distribución acumulada de los tiempos de retención del _IID Si . Un claro ejemplo es la paradoja del tiempo de espera de los autobuses : para una distribución aleatoria dada de llegadas de autobuses, el pasajero promedio en una parada de autobús observa más retrasos que el operador promedio de los autobuses.

La resolución de la paradoja es que nuestra distribución muestreada en el momento t está sesgada por el tamaño (ver sesgo de muestreo ), en el sentido de que la probabilidad de que se elija un intervalo es proporcional a su tamaño. Sin embargo, un intervalo de renovación de tamaño promedio no está sesgado por el tamaño.

Superposición

A menos que el proceso de renovación sea un proceso de Poisson, la superposición (suma) de dos procesos de renovación independientes no es un proceso de renovación. ^[7] Sin embargo, tales procesos pueden describirse dentro de una clase más amplia de procesos llamados procesos de renovación de Markov . ^[8] Sin embargo, la función de distribución acumulada del primer tiempo entre eventos en el proceso de superposición viene dada por ^[9]

${\displaystyle R(t)=1-\sum _{k=1}^{K}{\frac {\alpha _{k}}{\sum _{l=1}^{K}\alpha _{l}}}(1-R_{k}(t))\prod _{j=1,j\neq k}^{K}\alpha _{j}\int _{t}^{\infty }(1-R_{j}(u))\,{\text{d}}u}$

donde R _k ( t ) y α _k  > 0 son la CDF de los tiempos entre eventos y la tasa de llegada del proceso k . ^[10]

Aplicación de ejemplo

Eric, el empresario, tiene n máquinas, cada una con una vida operativa distribuida uniformemente entre cero y dos años. Eric puede dejar que cada máquina funcione hasta que falle y su reemplazo le costará 2600 €; alternativamente, puede sustituir una máquina en cualquier momento mientras aún esté en funcionamiento por un coste de 200 €.

¿Cuál es su política de reemplazo óptima?

Ver también

• Teorema de Campbell (probabilidad)
• Proceso de Poisson compuesto
• Proceso de Markov en tiempo continuo
• El lema de Little
• La ecuación integral de Lotka.
• Teorema de Palm-Khintchine
• proceso de veneno
• teoría de colas
• tiempo residual
• teoría de la ruina
• Proceso de Semi-Markov
• Ecuación de von Foerster

Notas

1. Grimmett y Stirzaker (1992), pág. 393.
2. Grimmett y Stirzaker (1992), pág. 390.
3. Grimmett y Stirzaker (1992), pág. 395.
4. Feller (1971), pág. 347–351.
5. Grimmett y Stirzaker (1992), pág. 394–5.
6. Grimmett y Stirzaker (1992), pág. 394.
7. Grimmett y Stirzaker (1992), pág. 405.
8. Çinlar, Erhan (1969). "Teoría de la renovación de Markov". Avances en probabilidad aplicada . Confianza de probabilidad aplicada. 1 (2): 123–187. doi :10.2307/1426216. JSTOR  1426216.
9. Lawrence, AJ (1973). "Dependencia de intervalos entre eventos en procesos de superposición". Revista de la Real Sociedad de Estadística. Serie B (Metodológica) . 35 (2): 306–315. doi :10.1111/j.2517-6161.1973.tb00960.x. JSTOR  2984914.fórmula 4.1
10. Choungmo Fofack, Nicaise; Naín, Philippe; Neglia, Giovanni; Towsley, Don (6 de marzo de 2012). Análisis de redes de caché basadas en TTL. Actas de la VI Conferencia Internacional sobre Metodologías y Herramientas de Evaluación del Desempeño (informe) . Consultado el 15 de noviembre de 2012 .

Referencias

• Cox, David (1970). Teoría de la renovación . Londres: Methuen & Co. p. 142.ISBN _ 0-412-20570-X.
• Doob, JL (1948). «Teoría de la renovación desde el punto de vista de la teoría de la probabilidad» (PDF) . Transacciones de la Sociedad Matemática Estadounidense . 63 (3): 422–438. doi : 10.2307/1990567 . JSTOR  1990567.
• Feller, William (1971). Una introducción a la teoría de la probabilidad y sus aplicaciones . vol. 2 (segunda ed.). Wiley.
• Grimmett, GR ; Stirzaker, DR (1992). Probabilidad y procesos aleatorios (segunda ed.). Prensa de la Universidad de Oxford. ISBN 0198572220.
• Smith, Walter L. (1958). "Teoría de la renovación y sus ramificaciones". Revista de la Royal Statistical Society, Serie B. 20 (2): 243–302. JSTOR  2983891.
• Wanli Wang, Johannes HP Schulz, Weihua Deng y Eli Barkai (2018). "Teoría de la renovación con tiempos de estancia distribuidos de cola gruesa: típico versus raro". Física. Rev. E. 98 (4): 042139. arXiv : 1809.05856 . Código bibliográfico : 2018PhRvE..98d2139W. doi : 10.1103/PhysRevE.98.042139. S2CID  54727926.{{cite journal}}: CS1 maint: multiple names: authors list (link)