Principio de Franck-Condon

El principio de Franck-Condon describe la intensidad de las transiciones vibrónicas, o la absorción o emisión de un fotón. Afirma que cuando una molécula experimenta una transición electrónica, como la ionización, la configuración nuclear de la molécula no experimenta ningún cambio significativo. ^[1]

Descripción general

**Figura 2.** Representación esquemática de los espectros de absorción y fluorescencia correspondientes al diagrama de energía de la Figura 1. La simetría se debe a la forma igual de los pozos de potencial de los estados excitado y fundamental. Las líneas estrechas normalmente sólo se pueden observar en los espectros de gases diluidos. Las curvas más oscuras representan el ensanchamiento no homogéneo de las mismas transiciones que se producen en líquidos y sólidos. Las transiciones electrónicas entre los niveles vibracionales más bajos de los estados electrónicos (la transición 0-0) tienen la misma energía tanto en la absorción como en la fluorescencia.

**Figura 3.** Analogía del péndulo semiclásico del principio de Franck-Condon. Se permiten transiciones vibrónicas en los puntos de inflexión clásicos porque tanto el momento como las coordenadas nucleares se corresponden en los dos niveles de energía representados. En esta ilustración, se favorecen las transiciones vibracionales 0-2.

El principio de Franck-Condon tiene una interpretación semiclásica bien establecida basada en las contribuciones originales de James Franck . ^[2] Las transiciones electrónicas son relativamente instantáneas en comparación con la escala de tiempo de los movimientos nucleares, por lo tanto, si la molécula se mueve a un nuevo nivel vibracional durante la transición electrónica, este nuevo nivel vibracional debe ser instantáneamente compatible con las posiciones nucleares y los momentos del nivel vibracional de la molécula en el estado electrónico original. En la imagen semiclásica de las vibraciones (oscilaciones) de un oscilador armónico simple, las condiciones necesarias pueden ocurrir en los puntos de giro, donde el momento es cero.

Clásicamente, el principio de Franck-Condon es la aproximación de que es más probable que ocurra una transición electrónica sin cambios en las posiciones de los núcleos en la entidad molecular y su entorno. El estado resultante se denomina estado de Franck-Condon y la transición involucrada, transición vertical. La formulación mecánico cuántica de este principio es que la intensidad de una transición vibrónica es proporcional al cuadrado de la integral de superposición entre las funciones de onda vibracionales de los dos estados que están involucrados en la transición.
— Compendio de terminología química de la IUPAC , 2.ª edición (1997)

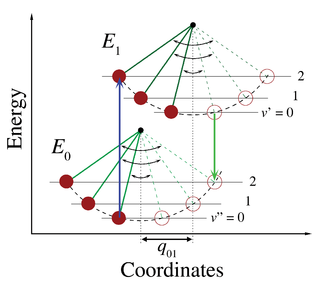
En la imagen mecánica cuántica , los niveles vibracionales y las funciones de onda vibracionales son los de los osciladores armónicos cuánticos , o de aproximaciones más complejas a la energía potencial de las moléculas, como el potencial de Morse . La Figura 1 ilustra el principio de Franck-Condon para transiciones vibrónicas en una molécula con funciones de energía potencial similares a Morse tanto en el estado electrónico fundamental como en el excitado. En la aproximación de baja temperatura, la molécula comienza en el nivel vibracional v = 0 del estado electrónico fundamental y al absorber un fotón de la energía necesaria, realiza una transición al estado electrónico excitado. La configuración electrónica del nuevo estado puede resultar en un cambio de la posición de equilibrio de los núcleos que constituyen la molécula. En la Figura 3, este cambio en las coordenadas nucleares entre el estado fundamental y el primer estado excitado se etiqueta como q ₀₁ . En el caso más simple de una molécula diatómica , el eje de coordenadas nucleares se refiere a la separación internuclear. La transición vibrónica se indica mediante una flecha vertical debido a la suposición de coordenadas nucleares constantes durante la transición. La probabilidad de que la molécula pueda terminar en un nivel vibracional particular es proporcional al cuadrado de la superposición (vertical) de las funciones de onda vibracionales del estado original y final (ver la sección de formulación de mecánica cuántica a continuación). En el estado electrónico excitado, las moléculas se relajan rápidamente al nivel vibracional más bajo del estado de excitación electrónica más bajo ( regla de Kasha ), y desde allí pueden decaer al estado electrónico fundamental mediante la emisión de fotones. El principio de Franck-Condon se aplica por igual a la absorción y a la fluorescencia .

La aplicabilidad del principio de Franck-Condon tanto en la absorción como en la fluorescencia, junto con la regla de Kasha, conduce a una simetría especular aproximada que se muestra en la Figura 2. La estructura vibracional de las moléculas en un gas frío y disperso es más claramente visible debido a la ausencia de ensanchamiento no homogéneo de las transiciones individuales. Las transiciones vibrónicas se dibujan en la Figura 2 como formas de línea de Lorentz angostas e igualmente espaciadas . El espaciamiento igual entre los niveles vibracionales solo se da en el caso del potencial parabólico de osciladores armónicos simples; en potenciales más realistas, como los que se muestran en la Figura 1, el espaciamiento de energía disminuye con el aumento de la energía vibracional. Las transiciones electrónicas hacia y desde los estados vibracionales más bajos a menudo se denominan transiciones 0-0 (cero cero) y tienen la misma energía tanto en la absorción como en la fluorescencia.

Desarrollo del principio

En un informe publicado en 1926 en Transactions of the Faraday Society , James Franck se ocupó de los mecanismos de las reacciones químicas inducidas por fotones. El supuesto mecanismo era la excitación de una molécula por un fotón, seguida de una colisión con otra molécula durante el corto período de excitación. La pregunta era si era posible que una molécula se rompiera en fotoproductos en un solo paso, la absorción de un fotón, y sin colisión. Para que una molécula se rompa, debe adquirir del fotón una energía vibratoria superior a la energía de disociación, es decir, la energía para romper un enlace químico. Sin embargo, como se sabía en ese momento, las moléculas solo absorberán energía correspondiente a las transiciones cuánticas permitidas, y no hay niveles vibratorios por encima del nivel de energía de disociación del pozo de potencial . La absorción de fotones de alta energía conduce a una transición a un estado electrónico superior en lugar de a la disociación. Al examinar cuánta energía vibracional podría adquirir una molécula cuando se la excita a un nivel electrónico superior, y si esta energía vibracional podría ser suficiente para romper inmediatamente la molécula, dibujó tres diagramas que representan los posibles cambios en la energía de enlace entre el estado electrónico más bajo y los estados electrónicos superiores.

El diagrama I muestra un gran debilitamiento de la unión en una transición del estado normal n a los estados excitados a y a ' . Aquí tenemos D > D' y D' > D". Al mismo tiempo, la posición de equilibrio de los núcleos se mueve con la excitación a mayores valores de r . Si pasamos de la posición de equilibrio (el mínimo de energía potencial) de la curva n verticalmente [énfasis añadido] hacia arriba a las curvas a en el diagrama I, las partículas tendrán una energía potencial mayor que D' y se separarán. En este caso tenemos un cambio muy grande en la energía de oscilación en la excitación por la luz...
—James Franck, 1926

James Franck reconoció que los cambios en los niveles vibracionales podrían ser una consecuencia de la naturaleza instantánea de la excitación a niveles de energía electrónica más altos y una nueva posición de equilibrio para el potencial de interacción nuclear. Edward Condon amplió esta idea más allá de las fotorreacciones en un artículo de Physical Review de 1926 titulado "Una teoría de la distribución de la intensidad en sistemas de bandas". ^[3] Aquí formula la formulación semiclásica de una manera bastante similar a su forma moderna. La primera referencia conjunta tanto a Franck como a Condon con respecto al nuevo principio aparece en el mismo número de 1926 de Physical Review en un artículo sobre la estructura de bandas del monóxido de carbono de Raymond Birge .

Formulación mecánica cuántica

Considérese una transición dipolar eléctrica desde el estado vibracional inicial ( υ ) del nivel electrónico fundamental ( ε ), , a algún estado vibracional ( υ ′) de un estado electrónico excitado ( ε ′), (véase la notación bra–ket ). El operador dipolar molecular μ está determinado por la carga (− e ) y las ubicaciones ( r _i ) de los electrones , así como por las cargas (+ Z _j e ) y las ubicaciones ( R _j ) de los núcleos : $|\epsilon v\rangle$ $|\epsilon 'v'\rangle$

{\boldsymbol {\mu }}={\boldsymbol {\mu }}_{e}+{\boldsymbol {\mu }}_{N}=-e\suma \límites _{i}{\boldsymbol {r}}_{i}+e\suma \límites _{j}Z_{j}{\boldsymbol {R}}_{j}.

La amplitud de probabilidad P para la transición entre estos dos estados está dada por

P=\left\langle \psi '\right|{\boldsymbol {\mu }}\left|\psi \right\rangle =\int {\psi '^{*}}{\boldsymbol {\mu }}\psi \,d\tau ,

donde y son, respectivamente, las funciones de onda globales del estado inicial y final. Las funciones de onda globales son el producto de las funciones de onda vibracionales (dependiendo de las coordenadas espaciales de los núcleos) y electrónicas del espacio y del espín : ${\estilo de visualización \psi}$ ${\estilo de visualización \psi '}$

\psi =\psi _{e}\psi _{v}\psi _{s}.

Esta separación de las funciones de onda electrónicas y vibracionales es una expresión de la aproximación de Born-Oppenheimer y es el supuesto fundamental del principio de Franck-Condon. La combinación de estas ecuaciones conduce a una expresión para la amplitud de probabilidad en términos de espacio electrónico separado, contribuciones de espín y vibracionales:

P=\left\langle \psi _{e}'\psi _{v}'\psi _{s}'\right|{\boldsymbol {\mu }}\left|\psi _{e}\psi _{v}\psi _{s}\right\rangle =\int \psi _{e}'^{*}\psi _{v}'^{*}\psi _{s}'^{*}({\boldsymbol {\mu }}_{e}+{\boldsymbol {\mu }}_{N})\psi _{e}\psi _{v}\psi _{s}\,d\tau

=\int \psi _{e}'^{*}\psi _{v}'^{*}\psi _{s}'^{*}{\boldsymbol {\mu }}_{e}\psi _{e}\psi _{v}\psi _{s}\,d\tau +\int \psi _{e}'^{*}\psi _{v}'^{*}\psi _{s}'^{*}{\boldsymbol {\mu }}_{N}\psi _{e}\psi _{v}\psi _{s}\,d\tau

=\underbrace {\int \psi _{v}'^{*}\psi _{v}\,d\tau _{n}} _{\displaystyle {{\text{Franck–Condon}} \atop {\text{factor}}}}\underbrace {\int \psi _{e}'^{*}{\boldsymbol {\mu }}_{e}\psi _{e}\,d\tau _{e}} _{\displaystyle {{\text{orbital}} \atop {\text{selection rule}}}}\underbrace {\int \psi _{s}'^{*}\psi _{s}\,d\tau _{s}} _{\displaystyle {{\text{spin}} \atop {\text{selection rule}}}}+\underbrace {\int \psi _{e}'^{*}\psi _{e}\,d\tau _{e}} _{\displaystyle 0}\int \psi _{v}'^{*}{\boldsymbol {\mu }}_{N}\psi _{v}\,d\tau _{v}\int \psi _{s}'^{*}\psi _{s}\,d\tau _{s}.

La parte independiente del espín de la integral inicial se aproxima aquí como un producto de dos integrales:

\iint \psi _{v}'^{*}\psi _{e}'^{*}{\boldsymbol {\mu }}_{e}\psi _{e}\psi _{v}\,d\tau _{e}d\tau _{n}\approx \int \psi _{v}'^{*}\psi _{v}\,d\tau _{n}\int \psi _{e}'^{*}{\boldsymbol {\mu }}_{e}\psi _{e}\,d\tau _{e}.

Esta factorización sería exacta si la integral sobre las coordenadas espaciales de los electrones no dependiera de las coordenadas nucleares. Sin embargo, en la aproximación de Born-Oppenheimer y sí dependen (paramétricamente) de las coordenadas nucleares, de modo que la integral (la denominada superficie dipolar de transición ) es una función de las coordenadas nucleares. Dado que la dependencia suele ser bastante suave, se descuida (es decir, a menudo se permite la suposición de que la superficie dipolar de transición es independiente de las coordenadas nucleares, llamada aproximación de Condon ). $\int \psi _{e}'^{*}{\boldsymbol {\mu }}_{e}\psi _{e}\,d\tau _{e}$ $\psi _{e}$ $\psi '_{e}$

La primera integral después del signo más es igual a cero porque las funciones de onda electrónicas de diferentes estados son ortogonales. El resto es el producto de tres integrales. La primera integral es la integral de superposición vibracional, también llamada factor de Franck-Condon . Las dos integrales restantes que contribuyen a la amplitud de probabilidad determinan las reglas de selección electrónica espacial y de espín.

El principio de Franck-Condon es una declaración sobre las transiciones vibracionales permitidas entre dos estados electrónicos diferentes ; otras reglas de selección de la mecánica cuántica pueden reducir la probabilidad de una transición o prohibirla por completo. En la derivación anterior se han ignorado las reglas de selección rotacional. Las contribuciones rotacionales se pueden observar en los espectros de los gases, pero están fuertemente suprimidas en líquidos y sólidos.

Debe quedar claro que la formulación mecánico cuántica del principio de Franck-Condon es el resultado de una serie de aproximaciones, principalmente el supuesto de transición dipolar eléctrica y la aproximación de Born-Oppenheimer. Las transiciones electrónicas dipolares magnéticas y cuadrupolos eléctricos más débiles , junto con la validez incompleta de la factorización de la función de onda total en funciones de onda nuclear, electrónica espacial y de espín, significa que las reglas de selección, incluido el factor de Franck-Condon, no se observan estrictamente. Para cualquier transición dada, el valor de P está determinado por todas las reglas de selección, sin embargo, la selección de espín es la que más contribuye, seguida de las reglas de selección electrónica. El factor de Franck-Condon solo modula débilmente la intensidad de las transiciones, es decir, contribuye con un factor del orden de 1 a la intensidad de las bandas cuyo orden de magnitud está determinado por las otras reglas de selección. La siguiente tabla muestra el rango de coeficientes de extinción para las posibles combinaciones de reglas de selección de espín y orbitales permitidas y prohibidas.

Metáforas de Franck-Condon en espectroscopia

El principio de Franck-Condon, en su forma canónica, se aplica únicamente a los cambios en los niveles vibracionales de una molécula en el curso de un cambio en los niveles electrónicos por absorción o emisión de un fotón. La intuición física de este principio se basa en la idea de que las coordenadas nucleares de los átomos que constituyen la molécula no tienen tiempo de cambiar durante el breve lapso de tiempo involucrado en una transición electrónica. Sin embargo, esta intuición física puede extenderse, y de hecho se extiende, rutinariamente a las interacciones entre las moléculas que absorben o emiten luz ( cromóforos ) y su entorno. Las metáforas de Franck-Condon son apropiadas porque las moléculas a menudo interactúan fuertemente con las moléculas circundantes, particularmente en líquidos y sólidos, y estas interacciones modifican las coordenadas nucleares del cromóforo de maneras muy análogas a las vibraciones moleculares consideradas por el principio de Franck-Condon.

Principio de Franck-Condon para fonones

La analogía de Franck-Condon más cercana se debe a la interacción de los fonones ( cuantos de vibraciones de la red ) con las transiciones electrónicas de los cromóforos incrustados como impurezas en la red. En esta situación, las transiciones a niveles electrónicos más altos pueden tener lugar cuando la energía del fotón corresponde a la energía de transición puramente electrónica o a la energía de transición puramente electrónica más la energía de uno o más fonones de la red. En la aproximación de baja temperatura, la emisión es desde el nivel de fonón cero del estado excitado al nivel de fonón cero del estado fundamental o a niveles de fonón más altos del estado fundamental. Al igual que en el principio de Franck-Condon, la probabilidad de transiciones que involucran fonones está determinada por la superposición de las funciones de onda de fonón en los niveles de energía inicial y final. Para el principio de Franck-Condon aplicado a las transiciones de fonones, la etiqueta del eje horizontal de la Figura 1 se reemplaza en la Figura 6 con la coordenada configuracional para un modo normal . La energía potencial del modo reticular en la Figura 6 se representa como la de un oscilador armónico, y el espaciamiento entre los niveles de fonones ( ) está determinado por los parámetros reticulares. Debido a que la energía de los fonones individuales es generalmente bastante pequeña, las transiciones de cero o pocos fonones solo se pueden observar a temperaturas inferiores a unos 40 kelvin . $q_{i}$ $\hbar \Omega _{i}$

Consulte Línea de fonón cero y banda lateral de fonón para obtener más detalles y referencias.

Principio de Franck-Condon en solvatación

Las consideraciones de Franck-Condon también se pueden aplicar a las transiciones electrónicas de los cromóforos disueltos en líquidos. En este uso de la metáfora de Franck-Condon, los niveles vibracionales de los cromóforos, así como las interacciones de los cromóforos con los fonones en el líquido, siguen contribuyendo a la estructura de los espectros de absorción y emisión, pero estos efectos se consideran por separado e independientemente.

Consideremos cromóforos rodeados de moléculas de disolvente . Estas moléculas circundantes pueden interactuar con los cromóforos, particularmente si las moléculas de disolvente son polares . Esta asociación entre disolvente y soluto se conoce como solvatación y es una interacción estabilizadora, es decir, las moléculas de disolvente pueden moverse y rotar hasta que se minimice la energía de la interacción. La interacción en sí implica fuerzas electrostáticas y de van der Waals y también puede incluir enlaces de hidrógeno . Los principios de Franck-Condon se pueden aplicar cuando las interacciones entre el cromóforo y las moléculas de disolvente circundantes son diferentes en el estado electrónico fundamental y en el excitado. Este cambio en la interacción puede originarse, por ejemplo, debido a diferentes momentos dipolares en estos dos estados. Si el cromóforo comienza en su estado fundamental y está cerca del equilibrio con las moléculas de disolvente circundantes y luego absorbe un fotón que lo lleva al estado excitado, su interacción con el disolvente estará lejos del equilibrio en el estado excitado. Este efecto es análogo al principio original de Franck-Condon: la transición electrónica es muy rápida en comparación con el movimiento de los núcleos (la reorganización de las moléculas de disolvente en el caso de la solvatación). Ahora hablamos de una transición vertical, pero ahora la coordenada horizontal es el espacio de interacción disolvente-soluto. Este eje de coordenadas se suele denominar "coordenada de solvatación" y representa, de forma un tanto abstracta, todas las dimensiones relevantes del movimiento de todas las moléculas de disolvente que interactúan.

En el principio original de Franck-Condon, después de la transición electrónica, las moléculas que terminan en estados vibracionales más altos comienzan inmediatamente a relajarse al estado vibracional más bajo. En el caso de la solvatación, las moléculas de solvente intentarán reorganizarse inmediatamente para minimizar la energía de interacción. La tasa de relajación del solvente depende de la viscosidad del solvente. Suponiendo que el tiempo de relajación del solvente es corto en comparación con la vida útil del estado electrónico excitado, la emisión será desde el estado de energía de solvente más bajo del estado electrónico excitado. Para solventes de moléculas pequeñas como agua o metanol a temperatura ambiente, el tiempo de relajación del solvente es del orden de algunas decenas de picosegundos , mientras que la vida útil del estado excitado del cromóforo varía de unos pocos picosegundos a unos pocos nanosegundos . Inmediatamente después de la transición al estado electrónico fundamental, las moléculas de solvente también deben reorganizarse para adaptarse a la nueva configuración electrónica del cromóforo. La Figura 7 ilustra el principio de Franck-Condon aplicado a la solvatación. Cuando la solución se ilumina con luz correspondiente a la energía de transición electrónica, algunos de los cromóforos se moverán al estado excitado. Dentro de este grupo de cromóforos habrá una distribución estadística de energías de interacción solvente-cromóforo, representada en la figura por una función de distribución gaussiana . La interacción solvente-cromóforo se dibuja como un potencial parabólico en ambos estados electrónicos. Dado que la transición electrónica es esencialmente instantánea en la escala de tiempo del movimiento del solvente (flecha vertical), el conjunto de cromóforos en estado excitado está inmediatamente lejos del equilibrio. La reorganización de las moléculas de solvente de acuerdo con la nueva curva de energía potencial está representada por las flechas curvas en la Figura 7. Nótese que mientras que las transiciones electrónicas están cuantificadas, la energía de interacción cromóforo-solvente se trata como un continuo clásico debido a la gran cantidad de moléculas involucradas. Aunque la emisión se representa como teniendo lugar desde el mínimo del potencial de interacción cromóforo-solvente en estado excitado, puede tener lugar una emisión significativa antes de que se alcance el equilibrio cuando la viscosidad del solvente es alta o la vida útil del estado excitado es corta. La diferencia de energía entre los fotones absorbidos y emitidos representada en la Figura 7 es la contribución de la solvatación al desplazamiento de Stokes .

Véase también

Referencias

^ https://chem.libretexts.org/Courses/Pacific_Union_College/Quantum_Chemistry/13%3A_Molecular_Spectroscopy/13.07%3A_The_Franck-Condon_Principle#:~:text=The%20Franck%2DCondon%20Principle%20describes,molecule%20experiences%20no%20significant% 20 cambio.
^ Franck, J. (1926). "Procesos elementales de reacciones fotoquímicas". Transactions of the Faraday Society . 21 : 536–542. doi :10.1039/tf9262100536.
^ Condon, Edward (1926-12-01). "Una teoría de la distribución de intensidad en sistemas de bandas". Physical Review . 28 (6): 1182–1201. Código Bibliográfico :1926PhRv...28.1182C. doi :10.1103/PhysRev.28.1182.

Lectura adicional

Franck, J. (1926). "Procesos elementales de reacciones fotoquímicas". Transactions of the Faraday Society . 21 : 536–542. doi :10.1039/tf9262100536.Enlace
Condon, E. (1926). "Una teoría de la distribución de intensidad en sistemas de bandas (Resumen de la reunión)". Physical Review . 27 (5): 640. Bibcode :1926PhRv...27..637.. doi :10.1103/PhysRev.27.637.
Condon, E. (1926). "Una teoría de la distribución de intensidad en sistemas de bandas". Physical Review . 28 (6): 1182–1201. Bibcode :1926PhRv...28.1182C. doi :10.1103/PhysRev.28.1182.Enlace archivado el 28 de diciembre de 2011 en Wayback Machine.
Condon, E. (1928). "Movimientos nucleares asociados con transiciones electrónicas en moléculas diatómicas". Physical Review . 32 (6): 858–872. Bibcode :1928PhRv...32..858C. doi :10.1103/PhysRev.32.858.Enlace archivado el 28 de diciembre de 2011 en Wayback Machine.
Birge, RT (1926). "Los espectros de banda del monóxido de carbono". Physical Review . 28 (6): 1157–1181. Bibcode :1926PhRv...28.1157B. doi :10.1103/PhysRev.28.1157.Enlace archivado el 28 de diciembre de 2011 en Wayback Machine.
Noyes, WA (1933). "La correlación de la espectroscopia y la fotoquímica". Reseñas de Física Moderna . 5 (4): 280–287. Bibcode :1933RvMP....5..280N. doi :10.1103/RevModPhys.5.280.Enlace
Coolidge, A. S, James, HM y Present, RD (1936). "Un estudio del principio de Franck-Condon". Journal of Chemical Physics . 4 (3): 193–211. Código Bibliográfico :1936JChPh...4..193C. doi :10.1063/1.1749818.{{cite journal}}: CS1 maint: multiple names: authors list (link)Enlace
Herzberg, Gerhard (1971). Los espectros y estructuras de los radicales libres simples . Nueva York: Dover . ISBN. 0-486-65821-X.
Harris, Daniel C.; Michael D. Bertolucci (1978). Simetría y espectroscopia . Nueva York: Dover. ISBN 0-486-66144-X.
Bernath, Peter F. (1995). Espectros de átomos y moléculas (Temas de química física) . Oxford: Oxford University Press . ISBN 0-19-507598-6.
Atkins, PW ; RS Friedman (1999). Mecánica cuántica molecular . Oxford: Oxford University Press. ISBN 0-19-855947-X.

Enlaces externos

Rabinowitch E.; Govindjee (1969). "Absorción de luz y destino de la energía de excitación: principio de Franck-Condon". Ciencias de la vida en la Universidad de Illinois en Urbana-Champaign . Consultado el 18 de mayo de 2024 .