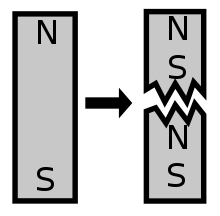
En física de partículas , un monopolo magnético es una partícula elemental hipotética que es un imán aislado con un solo polo magnético (un polo norte sin un polo sur o viceversa). [1] [2] Un monopolo magnético tendría una "carga magnética" neta norte o sur. El interés moderno en el concepto proviene de las teorías de partículas , en particular las teorías de gran unificación y de supercuerdas , que predicen su existencia. [3] [4] [ cita completa requerida ] Las partículas elementales conocidas que tienen carga eléctrica son monopolos eléctricos.
El magnetismo en los imanes de barra y en los electroimanes no es causado por monopolos magnéticos y, de hecho, no existe evidencia experimental u observacional conocida de que existan monopolos magnéticos.
Algunos sistemas de materia condensada contienen cuasipartículas monopolares magnéticas efectivas (no aisladas) [5] o contienen fenómenos que son matemáticamente análogos a los monopolos magnéticos. [6]
Muchos de los primeros científicos atribuyeron el magnetismo de las piedras imán a dos "fluidos magnéticos" ("efluvios") diferentes, un fluido del polo norte en un extremo y un fluido del polo sur en el otro, que se atraían y repelían entre sí en analogía con la carga eléctrica positiva y negativa . [7] [8] Sin embargo, una mejor comprensión del electromagnetismo en el siglo XIX mostró que el magnetismo de las piedras imán se explicaba adecuadamente no por fluidos monopolares magnéticos, sino más bien por una combinación de corrientes eléctricas , el momento magnético del electrón y los momentos magnéticos de otras partículas. La ley de Gauss para el magnetismo , una de las ecuaciones de Maxwell , es la afirmación matemática de que los monopolos magnéticos no existen. Sin embargo, Pierre Curie señaló en 1894 [9] que los monopolos magnéticos podrían existir, a pesar de que no se habían visto hasta ahora.
La teoría cuántica de la carga magnética comenzó con un artículo del físico Paul Dirac en 1931. [10] En este artículo, Dirac demostró que si existen monopolos magnéticos en el universo, entonces toda la carga eléctrica en el universo debe estar cuantizada (condición de cuantización de Dirac). [11] La carga eléctrica está , de hecho, cuantizada, lo que es consistente con (pero no prueba) la existencia de monopolos. [11]
Desde el artículo de Dirac, se han realizado varias búsquedas sistemáticas de monopolos. Los experimentos de 1975 [12] y 1982 [13] produjeron eventos candidatos que inicialmente se interpretaron como monopolos, pero que ahora se consideran no concluyentes. [14] Por lo tanto, si los monopolos existen sigue siendo una pregunta abierta. Los avances posteriores en la física teórica de partículas , en particular los desarrollos en las teorías de gran unificación y la gravedad cuántica , han llevado a argumentos más convincentes (detallados a continuación) de que los monopolos existen. Joseph Polchinski , un teórico de cuerdas, describió la existencia de monopolos como "una de las apuestas más seguras que uno puede hacer sobre la física aún no vista". [15] Estas teorías no son necesariamente inconsistentes con la evidencia experimental. En algunos modelos teóricos , es poco probable que se observen monopolos magnéticos, porque son demasiado masivos para crearse en aceleradores de partículas (ver § Búsquedas de monopolos magnéticos a continuación), y también demasiado raros en el Universo para entrar en un detector de partículas con mucha probabilidad. [15]
Algunos sistemas de materia condensada proponen una estructura superficialmente similar a un monopolo magnético, conocido como tubo de flujo . Los extremos de un tubo de flujo forman un dipolo magnético , pero dado que se mueven de forma independiente, pueden tratarse para muchos fines como cuasipartículas monopolares magnéticas independientes . Desde 2009, numerosos informes de noticias de los medios populares [16] [17] han descrito incorrectamente estos sistemas como el esperado descubrimiento de los monopolos magnéticos, pero los dos fenómenos solo están superficialmente relacionados entre sí. [18] [19] Estos sistemas de materia condensada siguen siendo un área de investigación activa. (Véase § "Monopolos" en sistemas de materia condensada a continuación.)
Toda la materia aislada hasta la fecha, incluidos todos los átomos de la tabla periódica y todas las partículas del Modelo Estándar , tiene carga monopolar magnética nula. Por lo tanto, los fenómenos ordinarios del magnetismo y los imanes no se derivan de los monopolos magnéticos.
En cambio, el magnetismo en la materia ordinaria se debe a dos fuentes. En primer lugar, las corrientes eléctricas crean campos magnéticos según la ley de Ampère . En segundo lugar, muchas partículas elementales tienen un momento magnético intrínseco , el más importante de los cuales es el momento dipolar magnético del electrón , que está relacionado con su espín mecánico-cuántico .
Matemáticamente, el campo magnético de un objeto se describe a menudo en términos de una expansión multipolar . Esta es una expresión del campo como la suma de los campos componentes con formas matemáticas específicas. El primer término en la expansión se llama término monopolar , el segundo se llama dipolo , luego cuadrupolo , luego octupolo , y así sucesivamente. Cualquiera de estos términos puede estar presente en la expansión multipolar de un campo eléctrico , por ejemplo. Sin embargo, en la expansión multipolar de un campo magnético , el término "monopolo" siempre es exactamente cero (para la materia ordinaria). Un monopolo magnético, si existe, tendría la propiedad definitoria de producir un campo magnético cuyo término monopolar no es cero.
Un dipolo magnético es algo cuyo campo magnético está predominantemente o exactamente descrito por el término dipolo magnético de la expansión multipolar. El término dipolo significa dos polos , lo que corresponde al hecho de que un imán dipolar típicamente contiene un polo norte en un lado y un polo sur en el otro lado. Esto es análogo a un dipolo eléctrico , que tiene carga positiva en un lado y carga negativa en el otro. Sin embargo, un dipolo eléctrico y un dipolo magnético son fundamentalmente bastante diferentes. En un dipolo eléctrico hecho de materia ordinaria, la carga positiva está hecha de protones y la carga negativa está hecha de electrones , pero un dipolo magnético no tiene diferentes tipos de materia que crean el polo norte y el polo sur. En cambio, los dos polos magnéticos surgen simultáneamente del efecto agregado de todas las corrientes y momentos intrínsecos en todo el imán. Debido a esto, los dos polos de un dipolo magnético siempre deben tener una fuerza igual y opuesta, y los dos polos no pueden separarse entre sí.
Las ecuaciones de Maxwell del electromagnetismo relacionan los campos eléctrico y magnético entre sí y con la distribución de la carga eléctrica y la corriente. Las ecuaciones estándar prevén la carga eléctrica, pero postulan que la carga magnética y la corriente son cero. Excepto por esta restricción, las ecuaciones son simétricas bajo el intercambio de los campos eléctrico y magnético . Las ecuaciones de Maxwell son simétricas cuando la carga y la densidad de corriente eléctrica son cero en todas partes, como en el vacío.
Las ecuaciones de Maxwell también pueden escribirse en una forma completamente simétrica si se permite una "carga magnética" análoga a la carga eléctrica. [20] Con la inclusión de una variable para la densidad de carga magnética, digamos ρ m , también hay una variable de " densidad de corriente magnética " en las ecuaciones, j m .
Si no existe carga magnética –o si existe pero está ausente en una región del espacio– entonces los nuevos términos en las ecuaciones de Maxwell son todos cero, y las ecuaciones extendidas se reducen a las ecuaciones convencionales del electromagnetismo tales como ∇ ⋅ B = 0 (donde ∇⋅ es el operador de divergencia y B es la densidad de flujo magnético ).
Las ecuaciones de Maxwell extendidas son las siguientes, en unidades CGS-Gaussianas : [23]
En estas ecuaciones, ρ m es la densidad de carga magnética , j m es la densidad de corriente magnética y q m es la carga magnética de una partícula de prueba, todas definidas de manera análoga a las cantidades relacionadas de carga eléctrica y corriente; v es la velocidad de la partícula y c es la velocidad de la luz . Para todas las demás definiciones y detalles, consulte las ecuaciones de Maxwell . Para las ecuaciones en forma no dimensionalizada , elimine los factores de c .
En el Sistema Internacional de Magnitudes utilizado con el SI , existen dos convenciones para definir la carga magnética q m , cada una con unidades diferentes: weber (Wb) y amperio -metro (A⋅m). La conversión entre ellas es q m [Wb] = μ 0 q m [A⋅m] , ya que las unidades son 1 Wb = 1 H⋅A = (1 H⋅m −1 )(1 A⋅m) , donde H es el henrio – la unidad SI de inductancia .
Las ecuaciones de Maxwell toman entonces las siguientes formas (usando la misma notación anterior): [notas 1]
Las ecuaciones de Maxwell también se pueden expresar en términos de potenciales de la siguiente manera:
dónde
Las ecuaciones de Maxwell en el lenguaje de los tensores dejan clara la covarianza de Lorentz . En este artículo, presentamos los tensores electromagnéticos y los cuatro vectores preliminares de la siguiente manera:
dónde:
Las ecuaciones generalizadas son: [25] [26]
Alternativamente, [27] [28]
donde ε αβμν es el símbolo de Levi-Civita .
Las ecuaciones generalizadas de Maxwell poseen una cierta simetría, llamada transformación de dualidad . Se puede elegir cualquier ángulo real ξ y, al mismo tiempo, cambiar los campos y las cargas en todas partes del universo de la siguiente manera (en unidades gaussianas): [29]
donde las cantidades con prima son las cargas y los campos antes de la transformación, y las cantidades sin prima son las posteriores a la transformación. Los campos y las cargas después de esta transformación siguen obedeciendo a las mismas ecuaciones de Maxwell.
Debido a la transformación de dualidad, no se puede decidir de manera única si una partícula tiene carga eléctrica, carga magnética o ambas, simplemente observando su comportamiento y comparándolo con las ecuaciones de Maxwell. Por ejemplo, es meramente una convención, no un requisito de las ecuaciones de Maxwell, que los electrones tengan carga eléctrica pero no carga magnética; después de una transformación ξ = π /2 , sería al revés. El hecho empírico clave es que todas las partículas observadas tienen la misma relación de carga magnética a carga eléctrica. [29] Las transformaciones de dualidad pueden cambiar la relación a cualquier valor numérico arbitrario, pero no pueden cambiar el hecho de que todas las partículas tengan la misma relación. Como este es el caso, se puede hacer una transformación de dualidad que fije esta relación en cero, de modo que todas las partículas no tengan carga magnética. Esta elección subyace a las definiciones "convencionales" de electricidad y magnetismo. [29]
Uno de los avances que definieron la teoría cuántica fue el trabajo de Paul Dirac sobre el desarrollo de un electromagnetismo cuántico relativista . Antes de su formulación, la presencia de carga eléctrica simplemente se "insertaba" en las ecuaciones de la mecánica cuántica (MC), pero en 1931 Dirac demostró que una carga discreta "cae" naturalmente fuera de la MC. [30] Es decir, podemos mantener la forma de las ecuaciones de Maxwell y aún tener cargas magnéticas.
Consideremos un sistema formado por un único monopolo eléctrico estacionario (un electrón, por ejemplo) y un único monopolo magnético estacionario, que no ejercerían ninguna fuerza entre sí. Clásicamente, el campo electromagnético que los rodea tiene una densidad de momento dada por el vector de Poynting , y también tiene un momento angular total , que es proporcional al producto q e q m , y es independiente de la distancia entre ellos.
Sin embargo, la mecánica cuántica dicta que el momento angular se cuantifica como un múltiplo de ħ , por lo que el producto q e q m también debe cuantificarse. Esto significa que si existiera un solo monopolo magnético en el universo y la forma de las ecuaciones de Maxwell fuera válida, todas las cargas eléctricas estarían cuantificadas .
Aunque sería posible simplemente integrar todo el espacio para encontrar el momento angular total en el ejemplo anterior, Dirac adoptó un enfoque diferente. Esto lo llevó a nuevas ideas. Consideró una carga magnética puntual cuyo campo magnético se comporta como¿ Quién soy?/r2 y está dirigida en dirección radial, ubicada en el origen. Debido a que la divergencia de B es igual a cero en todas partes excepto en el lugar geométrico del monopolo magnético en r = 0 , se puede definir localmente el potencial vectorial de manera que el rotacional del potencial vectorial A sea igual al campo magnético B .
Sin embargo, el potencial vectorial no puede definirse globalmente con precisión porque la divergencia del campo magnético es proporcional a la función delta de Dirac en el origen. Debemos definir un conjunto de funciones para el potencial vectorial en el "hemisferio norte" (el semiespacio z > 0 por encima de la partícula), y otro conjunto de funciones para el "hemisferio sur". Estos dos potenciales vectoriales coinciden en el "ecuador" (el plano z = 0 que pasa por la partícula), y difieren en una transformación de calibre . La función de onda de una partícula cargada eléctricamente (una "carga de sonda") que orbita el "ecuador" generalmente cambia en una fase, de forma muy similar al efecto Aharonov-Bohm . Esta fase es proporcional a la carga eléctrica q e de la sonda, así como a la carga magnética q m de la fuente. Dirac originalmente estaba considerando un electrón cuya función de onda está descrita por la ecuación de Dirac .
Como el electrón vuelve al mismo punto después de completar el recorrido alrededor del ecuador, la fase φ de su función de onda e iφ debe permanecer inalterada, lo que implica que la fase φ añadida a la función de onda debe ser un múltiplo de 2 π . Esto se conoce como condición de cuantificación de Dirac . En varias unidades, esta condición se puede expresar como:
donde ε 0 es la permitividad del vacío , ħ = h /2 π es la constante de Planck reducida , c es la velocidad de la luz y es el conjunto de números enteros .
La existencia hipotética de un monopolo magnético implicaría que la carga eléctrica debe estar cuantificada en ciertas unidades; además, la existencia de las cargas eléctricas implica que las cargas magnéticas de los monopolos magnéticos hipotéticos, si existen, deben estar cuantificadas en unidades inversamente proporcionales a la carga eléctrica elemental.
En aquel momento no estaba claro si tal cosa existía, o siquiera si tenía que existir. Después de todo, podría surgir otra teoría que explicara la cuantificación de carga sin necesidad del monopolo. El concepto siguió siendo una curiosidad. Sin embargo, desde la publicación de este trabajo seminal, no ha aparecido ninguna otra explicación ampliamente aceptada de la cuantificación de carga. (El concepto de invariancia de calibre local —véase teoría de calibre— proporciona una explicación natural de la cuantificación de carga, sin invocar la necesidad de monopolos magnéticos; pero solo si el grupo de calibre U(1) es compacto, en cuyo caso tenemos monopolos magnéticos de todos modos).
Si ampliamos al máximo la definición del potencial vectorial para el hemisferio sur, se define en todas partes excepto en una línea semiinfinita que se extiende desde el origen en dirección al polo norte. Esta línea semiinfinita se llama cuerda de Dirac y su efecto sobre la función de onda es análogo al efecto del solenoide en el efecto Aharonov-Bohm . La condición de cuantificación proviene del requisito de que las fases alrededor de la cuerda de Dirac sean triviales, lo que significa que la cuerda de Dirac debe ser no física. La cuerda de Dirac es simplemente un artefacto del diagrama de coordenadas utilizado y no debe tomarse en serio.
El monopolo de Dirac es una solución singular de la ecuación de Maxwell (porque requiere eliminar la línea de mundo del espacio-tiempo); en teorías más sofisticadas, es reemplazado por una solución suave como el monopolo de 't Hooft-Polyakov .
Una teoría de calibre, como el electromagnetismo, se define por un campo de calibre, que asocia un elemento de grupo a cada trayectoria en el espacio-tiempo. Para trayectorias infinitesimales, el elemento de grupo está cerca de la identidad, mientras que para trayectorias más largas, el elemento de grupo es el producto sucesivo de los elementos de grupo infinitesimales a lo largo del camino.
En electrodinámica, el grupo es U(1) , números complejos unitarios bajo multiplicación. Para trayectorias infinitesimales, el elemento del grupo es 1 + iA μ dx μ lo que implica que para trayectorias finitas parametrizadas por s , el elemento del grupo es:
El mapa de trayectorias a elementos del grupo se denomina bucle de Wilson o holonomía y, para un grupo de calibración U(1), es el factor de fase que adquiere la función de onda de una partícula cargada a medida que recorre la trayectoria. Para un bucle:
De modo que la fase que adquiere una partícula cargada al pasar por un bucle es el flujo magnético que atraviesa el bucle. Cuando un solenoide pequeño tiene un flujo magnético, hay franjas de interferencia para las partículas cargadas que giran alrededor del solenoide, o alrededor de diferentes lados del solenoide, que revelan su presencia.
Pero si todas las cargas de las partículas son múltiplos enteros de e , los solenoides con un flujo de 2 π / e no tienen franjas de interferencia, porque el factor de fase para cualquier partícula cargada es exp(2 π i ) = 1 . Un solenoide de este tipo, si es lo suficientemente delgado, es invisible desde el punto de vista mecánico cuántico. Si un solenoide de este tipo tuviera un flujo de 2 π / e , cuando el flujo se filtrara por uno de sus extremos, sería indistinguible de un monopolo.
La solución monopolar de Dirac describe, de hecho, un solenoide de línea infinitesimal que termina en un punto, y la ubicación del solenoide es la parte singular de la solución, la cuerda de Dirac. Las cuerdas de Dirac vinculan monopolos y antimonopolos de carga magnética opuesta, aunque en la versión de Dirac, la cuerda simplemente se extiende hasta el infinito. La cuerda es inobservable, por lo que se puede colocar en cualquier lugar, y al usar dos parches de coordenadas, el campo en cada parche se puede hacer no singular deslizando la cuerda hasta donde no se pueda ver.
En un grupo de calibración U(1) con carga cuantificada, el grupo es un círculo de radio 2 π / e . Un grupo de calibración U(1) de este tipo se denomina compacto . Cualquier U(1) que provenga de una teoría unificada de gran magnitud (GUT) es compacto, porque solo los grupos de calibración compactos de mayor magnitud tienen sentido. El tamaño del grupo de calibración es una medida de la constante de acoplamiento inversa, de modo que en el límite de un grupo de calibración de gran volumen, la interacción de cualquier representación fija tiende a cero.
El caso del grupo de calibración U(1) es un caso especial porque todas sus representaciones irreducibles son del mismo tamaño –la carga es mayor en una cantidad entera, pero el campo sigue siendo simplemente un número complejo–, de modo que en la teoría de campos de calibración U(1) es posible tomar el límite descompactado sin ninguna contradicción. El cuanto de carga se vuelve pequeño, pero cada partícula cargada tiene una enorme cantidad de cuantos de carga, de modo que su carga permanece finita. En una teoría de grupo de calibración U(1) no compacta, las cargas de las partículas no son, genéricamente, múltiplos enteros de una sola unidad. Dado que la cuantificación de la carga es una certeza experimental, está claro que el grupo de calibración U(1) del electromagnetismo es compacto.
Las GUT dan lugar a grupos de calibración U(1) compactos, por lo que explican la cuantificación de carga de una manera que parece lógicamente independiente de los monopolos magnéticos. Sin embargo, la explicación es esencialmente la misma, porque en cualquier GUT que se descomponga en un grupo de calibración U(1) a grandes distancias, hay monopolos magnéticos.
El argumento es topológico:
Por lo tanto, el monopolo de Dirac es un defecto topológico en una teoría de calibración compacta U(1). Cuando no hay GUT, el defecto es una singularidad: el núcleo se encoge hasta un punto. Pero cuando hay algún tipo de regulador de corta distancia en el espacio-tiempo, los monopolos tienen una masa finita. Los monopolos se dan en la red U(1) , y allí el tamaño del núcleo es el tamaño de la red. En general, se espera que se den siempre que haya un regulador de corta distancia.
En el universo, la gravedad cuántica proporciona el regulador. Cuando se incluye la gravedad, la singularidad monopolar puede ser un agujero negro, y para una gran carga magnética y masa, la masa del agujero negro es igual a la carga del agujero negro, de modo que la masa del agujero negro magnético no es infinita. Si el agujero negro puede desintegrarse completamente mediante la radiación de Hawking , las partículas cargadas más ligeras no pueden ser demasiado pesadas. [32] El monopolo más ligero debería tener una masa menor o comparable a su carga en unidades naturales .
Por lo tanto, en una teoría holográfica consistente, de la que la teoría de cuerdas es el único ejemplo conocido, siempre hay monopolos de masa finita. Para el electromagnetismo ordinario, el límite superior de masa no es muy útil porque es aproximadamente del mismo tamaño que la masa de Planck .
En matemáticas, un campo de calibración (clásico) se define como una conexión sobre un haz G principal a lo largo del espacio-tiempo. G es el grupo de calibración y actúa sobre cada fibra del haz por separado.
Una conexión en un fibrado G indica cómo unir fibras en puntos cercanos de M. Comienza con un grupo de simetría continuo G que actúa sobre la fibra F y luego asocia un elemento de grupo con cada camino infinitesimal. La multiplicación de grupos a lo largo de cualquier camino indica cómo moverse de un punto del fibrado a otro, al hacer que el elemento G asociado a un camino actúe sobre la fibra F.
En matemáticas, la definición de fibrado está diseñada para enfatizar la topología, por lo que la noción de conexión se agrega como una ocurrencia posterior. En física, la conexión es el objeto físico fundamental. Una de las observaciones fundamentales en la teoría de clases características en topología algebraica es que muchas estructuras homotópicas de fibrados principales no triviales pueden expresarse como una integral de algún polinomio sobre cualquier conexión sobre él. Nótese que una conexión sobre un fibrado trivial nunca puede darnos un fibrado principal no trivial.
Si el espacio-tiempo es el espacio de todas las conexiones posibles del haz G, está conexo . Pero consideremos lo que sucede cuando eliminamos una línea de mundo temporal del espacio-tiempo. El espacio-tiempo resultante es homotópicamente equivalente a la esfera topológica S 2 .
Un fibrado principal G sobre S 2 se define cubriendo S 2 con dos cartas , cada una homeomorfa a la 2-bola abierta de modo que su intersección es homeomorfa a la tira S 1 × I . Las 2-bolas son homotópicamente triviales y la tira es homotópicamente equivalente al círculo S 1 . Por lo tanto, una clasificación topológica de las posibles conexiones se reduce a clasificar las funciones de transición. La función de transición asigna la tira a G , y las diferentes formas de asignar una tira a G están dadas por el primer grupo de homotopía de G .
Así, en la formulación del fibrado G , una teoría de calibración admite monopolos de Dirac siempre que G no esté simplemente conexo , siempre que haya caminos que rodeen al grupo que no puedan deformarse en un camino constante (un camino cuya imagen consiste en un único punto). U(1), que tiene cargas cuantizadas, no está simplemente conexo y puede tener monopolos de Dirac, mientras que , su grupo de recubrimiento universal , está simplemente conexo, no tiene cargas cuantizadas y no admite monopolos de Dirac. La definición matemática es equivalente a la definición física siempre que, siguiendo a Dirac, se permitan campos de calibración que se definan solo por parches, y el campo de calibración en diferentes parches se pegue después de una transformación de calibración.
El flujo magnético total no es otro que el primer número de Chern del fibrado principal y depende únicamente de la elección del fibrado principal y no de la conexión específica sobre él. En otras palabras, es un invariante topológico.
Este argumento a favor de los monopolos es una reformulación del argumento del lazo a favor de una teoría U(1) pura. Se generaliza a dimensiones d + 1 con d ≥ 2 de varias maneras. Una forma es extender todo a las dimensiones adicionales, de modo que los monopolos U(1) se conviertan en láminas de dimensión d − 3 . Otra forma es examinar el tipo de singularidad topológica en un punto con el grupo de homotopía π d −2 (G) .
En años más recientes, una nueva clase de teorías también ha sugerido la existencia de monopolos magnéticos.
A principios de la década de 1970, los éxitos de la teoría cuántica de campos y la teoría de gauge en el desarrollo de la teoría electrodébil y las matemáticas de la fuerza nuclear fuerte llevaron a muchos teóricos a intentar combinarlas en una única teoría conocida como teoría unificada de gran magnitud (GUT). Se propusieron varias GUT, la mayoría de las cuales implicaban la presencia de una partícula monopolar magnética real. Más exactamente, las GUT predijeron una gama de partículas conocidas como diones , de las cuales el estado más básico era un monopolo. La carga de los monopolos magnéticos predicha por las GUT es de 1 o 2 gD , dependiendo de la teoría.
La mayoría de las partículas que aparecen en cualquier teoría cuántica de campos son inestables y se desintegran en otras partículas mediante diversas reacciones que deben satisfacer diversas leyes de conservación . Las partículas estables lo son porque no hay partículas más ligeras en las que puedan desintegrarse y que, aun así, cumplan las leyes de conservación. Por ejemplo, el electrón tiene un número leptónico de uno y una carga eléctrica de uno, y no hay partículas más ligeras que conserven estos valores. Por otro lado, el muón , que es esencialmente un electrón pesado, puede desintegrarse en el electrón más dos cuantos de energía y, por lo tanto, no es estable.
Los diones en estas GUT también son estables, pero por una razón completamente diferente. Se espera que los diones existan como un efecto secundario de la "congelación" de las condiciones del universo primitivo, o una ruptura de simetría . En este escenario, los diones surgen debido a la configuración del vacío en un área particular del universo, de acuerdo con la teoría original de Dirac. Permanecen estables no debido a una condición de conservación, sino porque no hay un estado topológico más simple en el que puedan decaer.
La escala de longitud en la que existe esta configuración especial de vacío se denomina longitud de correlación del sistema. Una longitud de correlación no puede ser mayor que la que permitiría la causalidad , por lo tanto, la longitud de correlación para formar monopolos magnéticos debe ser al menos tan grande como el tamaño del horizonte determinado por la métrica del universo en expansión . Según esa lógica, debería haber al menos un monopolo magnético por volumen de horizonte como lo había cuando se produjo la ruptura de la simetría.
Los modelos cosmológicos de los acontecimientos posteriores al Big Bang hacen predicciones sobre cuál era el volumen del horizonte, lo que conduce a predicciones sobre la densidad de monopolos actual. Los primeros modelos predijeron una enorme densidad de monopolos, en clara contradicción con la evidencia experimental. [33] [34] Esto se llamó el " problema del monopolo ". Su resolución ampliamente aceptada no fue un cambio en la predicción de monopolos de la física de partículas, sino más bien en los modelos cosmológicos utilizados para inferir su densidad actual. En concreto, las teorías más recientes de la inflación cósmica reducen drásticamente el número predicho de monopolos magnéticos, a una densidad lo suficientemente pequeña como para que no sea sorprendente que los humanos nunca hayan visto uno. [35] Esta resolución del "problema del monopolo" se consideró un éxito de la teoría de la inflación cósmica . (Sin embargo, por supuesto, sólo es un éxito notable si la predicción del monopolo de la física de partículas es correcta. [36] ) Por estas razones, los monopolos se convirtieron en un interés importante en los años 1970 y 1980, junto con las otras predicciones "accesibles" de las GUT como la desintegración de protones .
Muchas de las otras partículas predichas por estas GUT estaban más allá de la capacidad de detección de los experimentos actuales. Por ejemplo, se predice que una amplia clase de partículas conocidas como los bosones X e Y median el acoplamiento de las fuerzas electrodébil y fuerte, pero estas partículas son extremadamente pesadas y están muy fuera de la capacidad de creación de cualquier acelerador de partículas razonable.
Las búsquedas experimentales de monopolos magnéticos se pueden clasificar en una de dos categorías: las que intentan detectar monopolos magnéticos preexistentes y las que intentan crear y detectar nuevos monopolos magnéticos.
Al pasar un monopolo magnético a través de una bobina de alambre se induce una corriente neta en la bobina. Esto no sucede en el caso de un dipolo magnético o un polo magnético de orden superior, para los cuales la corriente neta inducida es cero y, por lo tanto, el efecto puede utilizarse como una prueba inequívoca de la presencia de monopolos magnéticos. En un alambre con resistencia finita, la corriente inducida disipa rápidamente su energía en forma de calor, pero en un bucle superconductor la corriente inducida es de larga duración. Mediante el uso de un "dispositivo de interferencia cuántica superconductor" ( SQUID ) de alta sensibilidad, en principio se puede detectar incluso un solo monopolo magnético.
Según la cosmología inflacionaria estándar, los monopolos magnéticos producidos antes de la inflación se habrían diluido hasta alcanzar una densidad extremadamente baja en la actualidad. También es posible que se hayan producido monopolos magnéticos térmicamente después de la inflación, durante el período de recalentamiento. Sin embargo, los límites actuales de la temperatura de recalentamiento abarcan 18 órdenes de magnitud y, en consecuencia, la densidad de monopolos magnéticos actuales no está bien limitada por la teoría.
Se han llevado a cabo muchas búsquedas de monopolos magnéticos preexistentes. Aunque se ha registrado un suceso fascinante, realizado por Blas Cabrera Navarro en la noche del 14 de febrero de 1982 (por lo que a veces se lo denomina el " Monopolo del día de San Valentín " [37] ), nunca ha habido evidencia reproducible de la existencia de monopolos magnéticos. [13] La falta de tales eventos impone un límite superior al número de monopolos de aproximadamente un monopolo por cada 10 29 nucleones .
Otro experimento en 1975 resultó en el anuncio de la detección de un monopolo magnético en movimiento en los rayos cósmicos por el equipo dirigido por P. Buford Price . [12] Price más tarde se retractó de su afirmación, y una posible explicación alternativa fue ofrecida por Luis Walter Alvarez . [38] En su artículo se demostró que la trayectoria del evento de rayos cósmicos que se afirmaba que se debía a un monopolo magnético podía reproducirse mediante la trayectoria seguida por un núcleo de platino que se desintegra primero en osmio y luego en tantalio .
Los colisionadores de partículas de alta energía se han utilizado para intentar crear monopolos magnéticos. Debido a la conservación de la carga magnética, los monopolos magnéticos deben crearse en pares, uno norte y otro sur. Debido a la conservación de la energía, solo se pueden producir monopolos magnéticos con masas inferiores a la mitad de la energía del centro de masas de las partículas en colisión. Más allá de esto, se sabe muy poco teóricamente sobre la creación de monopolos magnéticos en colisiones de partículas de alta energía. Esto se debe a su gran carga magnética, que invalida todas las técnicas de cálculo habituales. Como consecuencia, las búsquedas de monopolos magnéticos basadas en colisionadores no pueden, hasta ahora, proporcionar límites inferiores para la masa de los monopolos magnéticos. Sin embargo, pueden proporcionar límites superiores para la probabilidad (o sección transversal) de producción de pares, en función de la energía.
El experimento ATLAS del Gran Colisionador de Hadrones tiene actualmente los límites de sección eficaz más estrictos para monopolos magnéticos de 1 y 2 cargas de Dirac, producidos mediante la producción de pares Drell-Yan . Un equipo dirigido por Wendy Taylor busca estas partículas basándose en teorías que las definen como de larga vida (no se desintegran rápidamente), además de ser altamente ionizantes (su interacción con la materia es predominantemente ionizante). En 2019, la búsqueda de monopolos magnéticos en el detector ATLAS informó sus primeros resultados a partir de datos recopilados de las colisiones Run 2 del LHC a una energía del centro de masas de 13 TeV, que con 34,4 fb −1 es el conjunto de datos más grande analizado hasta la fecha. [39]
El experimento MoEDAL , instalado en el Gran Colisionador de Hadrones, busca actualmente monopolos magnéticos y partículas supersimétricas de gran tamaño utilizando detectores de trazas nucleares y barras de aluminio alrededor del detector VELO del LHCb . Las partículas que busca dañan las láminas de plástico que componen los detectores de trazas nucleares a lo largo de su trayectoria, con diversas características identificativas. Además, las barras de aluminio pueden atrapar monopolos magnéticos que se mueven con suficiente lentitud. Las barras pueden luego analizarse pasándolas a través de un SQUID.
Desde aproximadamente 2003, varios grupos de física de la materia condensada han utilizado el término "monopolo magnético" para describir un fenómeno diferente y en gran medida no relacionado. [18] [19]
Un monopolo magnético verdadero sería una nueva partícula elemental y violaría la ley de Gauss para el magnetismo ∇⋅ B = 0. Un monopolo de este tipo, que ayudaría a explicar la ley de cuantificación de carga formulada por Paul Dirac en 1931, [40] nunca se ha observado en experimentos. [41] [42]
Los monopolos estudiados por los grupos de materia condensada no tienen ninguna de estas propiedades. No son una nueva partícula elemental, sino más bien un fenómeno emergente en sistemas de partículas cotidianas ( protones , neutrones , electrones , fotones ); en otras palabras, son cuasipartículas . No son fuentes para el campo B (es decir, no violan ∇⋅ B = 0 ); en cambio, son fuentes para otros campos, por ejemplo el campo H , [5] el " campo B * " (relacionado con la vorticidad superfluida ), [6] [43] o varios otros campos cuánticos. [44] No son directamente relevantes para las grandes teorías unificadas u otros aspectos de la física de partículas, y no ayudan a explicar la cuantificación de carga , excepto en la medida en que los estudios de situaciones análogas puedan ayudar a confirmar que los análisis matemáticos involucrados son sólidos. [45]
Hay varios ejemplos en la física de la materia condensada donde el comportamiento colectivo conduce a fenómenos emergentes que se parecen a los monopolos magnéticos en ciertos aspectos, [17] [46] [47] [48] incluyendo, más prominentemente, los materiales de hielo de espín . [5] [49] Si bien estos no deben confundirse con los monopolos elementales hipotéticos que existen en el vacío, no obstante tienen propiedades similares y pueden investigarse utilizando técnicas similares.
Algunos investigadores utilizan el término magnetricidad para describir la manipulación de cuasipartículas monopolares magnéticas en el hielo de espín , [50] [51] [49] [52] en analogía con la palabra "electricidad".
Un ejemplo del trabajo sobre cuasipartículas monopolares magnéticas es un artículo publicado en la revista Science en septiembre de 2009, en el que los investigadores describieron la observación de cuasipartículas que se asemejaban a monopolos magnéticos. Un monocristal del material de hielo de espín titanato de disprosio se enfrió a una temperatura entre 0,6 kelvin y 2,0 kelvin. Utilizando observaciones de dispersión de neutrones , se demostró que los momentos magnéticos se alineaban en haces entrelazados con forma de tubo que se asemejaban a cuerdas de Dirac . En el defecto formado por el extremo de cada tubo, el campo magnético se parece al de un monopolo. Utilizando un campo magnético aplicado para romper la simetría del sistema, los investigadores pudieron controlar la densidad y la orientación de estas cuerdas. También se describió una contribución a la capacidad térmica del sistema a partir de un gas efectivo de estas cuasipartículas. [16] [53] Esta investigación ganó el Premio Europhysics 2012 de física de la materia condensada.
En otro ejemplo, un artículo publicado en la edición del 11 de febrero de 2011 de Nature Physics describe la creación y medición de corrientes de cuasipartículas magnéticas monopolares de larga duración en hielo de espín. Al aplicar un pulso de campo magnético a un cristal de titanato de disprosio a 0,36 K, los autores crearon una corriente magnética relajante que duró varios minutos. Midieron la corriente mediante la fuerza electromotriz que indujo en un solenoide acoplado a un amplificador sensible y la describieron cuantitativamente utilizando un modelo cinético químico de cargas puntuales que obedecen al mecanismo de Onsager-Wien de disociación y recombinación de portadores. De este modo, derivaron los parámetros microscópicos del movimiento monopolar en el hielo de espín e identificaron los distintos papeles de las cargas magnéticas libres y ligadas. [52]
En los superfluidos , existe un campo B * , relacionado con la vorticidad superfluida, que es matemáticamente análogo al campo magnético B. Debido a la similitud, el campo B * se denomina "campo magnético sintético". En enero de 2014, se informó que se crearon y estudiaron cuasipartículas monopolares [54] para el campo B * en un condensado de Bose-Einstein de espinores. [6] Esto constituye el primer ejemplo de un monopolo cuasimagnético observado dentro de un sistema gobernado por la teoría cuántica de campos. [45]
Las actualizaciones de las búsquedas teóricas y experimentales en la materia se pueden encontrar en los informes de G. Giacomelli (2000) y de S. Balestra (2011) en la sección Bibliografía.
Esta no es la primera vez que los físicos han creado análogos de monopolos. En 2009, los físicos observaron monopolos magnéticos en un material cristalino llamado hielo de espín, que, cuando se enfría hasta casi el cero absoluto, parece llenarse de monopolos clásicos del tamaño de un átomo. Estos son magnéticos en un sentido verdadero, pero no se pueden estudiar individualmente. También se han visto análogos similares en otros materiales, como en el helio superfluido. ... Steven Bramwell, físico del University College de Londres que fue pionero en el estudio de monopolos en hielos de espín, dice que el experimento [de 2014 dirigido por David Hall] es impresionante, pero que lo que se observó no es un monopolo de Dirac en el sentido en que mucha gente podría entenderlo. "Hay una analogía matemática aquí, una analogía clara y hermosa. Pero no son monopolos magnéticos".
Los monopolos magnéticos también han inspirado a los físicos de la materia condensada a descubrir estados y excitaciones análogos en sistemas como los hielos de espín y los condensados de Bose-Einstein. Sin embargo, a pesar de la importancia de esos desarrollos en sus propios campos, no resuelven la cuestión de la existencia de monopolos magnéticos reales. Por lo tanto, la búsqueda continúa.
Este artículo incorpora material de N. Hitchin (2001) [1994], "Monopolo magnético", Enciclopedia de matemáticas , EMS Press, que se encuentra bajo la licencia Creative Commons Attribution/Share-Alike y la Licencia de Documentación Libre de GNU .