Isometría del plano euclidiano

En geometría , una isometría del plano euclidiano es una isometría del plano euclidiano o, de manera más informal, una forma de transformar el plano que conserva propiedades geométricas como la longitud. Existen cuatro tipos: traslaciones , rotaciones , reflexiones y reflexiones de deslizamiento (consulte más adelante el apartado Clasificación).

El conjunto de isometrías del plano euclidiano forma un grupo de composición : el grupo euclidiano en dos dimensiones. Se genera por reflexiones en líneas y cada elemento del grupo euclidiano es la composición de, como máximo, tres reflexiones distintas.

Discusión informal

De manera informal, una isometría del plano euclidiano es cualquier forma de transformar el plano sin "deformarlo". Por ejemplo, supongamos que el plano euclidiano está representado por una lámina de plástico transparente colocada sobre un escritorio. Algunos ejemplos de isometrías son:

• Desplazando la hoja una pulgada hacia la derecha.
• Girar la hoja diez grados alrededor de un punto marcado (que permanece inmóvil).
• Dando vuelta la hoja para mirarla desde atrás. Observe que si se dibuja un dibujo en un lado de la hoja, luego de dar vuelta la hoja, vemos la imagen reflejada del dibujo.

Estos son ejemplos de traslaciones , rotaciones y reflexiones respectivamente. Existe otro tipo de isometría, llamada reflexión de deslizamiento (ver más abajo la clasificación de las isometrías del plano euclidiano).

Sin embargo, doblar, cortar o fundir la lámina no se consideran isometrías, como tampoco lo son alteraciones menos drásticas como doblarla, estirarla o torcerla.

Definición formal

Una isometría del plano euclidiano es una transformación del plano que preserva la distancia. Es decir, es una función

$${\displaystyle M:{\textbf {R}}^{2}\to {\textbf {R}}^{2}}$$

de manera que para cualesquiera puntos p y q en el plano,

$${\displaystyle d(p,q)=d(M(p),M(q)),}$$

donde d ( p , q ) es la distancia euclidiana habitual entre p y q .

Clasificación

Se puede demostrar que hay cuatro tipos de isometrías del plano euclidiano. ( Nota : las notaciones para los tipos de isometrías que se enumeran a continuación no están completamente estandarizadas).

Reflexiones

Reflexión

Las reflexiones , o isometrías especulares , denotadas por F _{c , v} , donde c es un punto en el plano y v es un vector unitario en R ² . ( F significa "flip".) tienen el efecto de reflejar el punto p en la línea L que es perpendicular a v y que pasa por c . La línea L se llama eje de reflexión o espejo asociado. Para encontrar una fórmula para F _{c , v} , primero usamos el producto escalar para encontrar el componente t de p − c en la dirección v ,

$${\displaystyle t=(p-c)\cdot v=(p_{x}-c_{x})v_{x}+(p_{y}-c_{y})v_{y},}$$

y luego obtenemos el reflejo de p por sustracción,

$${\displaystyle F_{c,v}(p)=p-2tv.}$$

La combinación de rotaciones sobre el origen y reflexiones sobre una línea que pasa por el origen se obtiene con todas las matrices ortogonales (es decir, con determinante 1 y −1) formando el grupo ortogonal O (2). En el caso de un determinante de −1 tenemos:

$${\displaystyle R_{0,\theta }(p)={\begin{bmatrix}\cos \theta &\sin \theta \\\sin \theta &\mathbf {-} \cos \theta \end{bmatrix}}{\begin{bmatrix}p_{x}\\p_{y}\end{bmatrix}}.}$$que es una reflexión en el eje x seguida de una rotación en un ángulo θ , o equivalentemente, una reflexión en una línea que forma un ángulo θ /2 con el eje x . La reflexión en una línea paralela corresponde a la suma de un vector perpendicular a ella.

Traducciones

Traducción

Las traslaciones , denotadas por T _v , donde v es un vector en R ² tienen el efecto de desplazar el plano en la dirección de v . Es decir, para cualquier punto p en el plano,

$${\displaystyle T_{v}(p)=p+v,}$$

o en términos de coordenadas ( x , y ),

$${\displaystyle T_{v}(p)={\begin{bmatrix}p_{x}+v_{x}\\p_{y}+v_{y}\end{bmatrix}}.}$$

Una traducción puede verse como una combinación de dos reflexiones paralelas.

Rotaciones

Rotación

Rotaciones , denotadas por R _c,θ , donde c es un punto en el plano (el centro de rotación), y θ es el ángulo de rotación. En términos de coordenadas, las rotaciones se expresan más fácilmente dividiéndolas en dos operaciones. Primero, una rotación alrededor del origen está dada por

$${\displaystyle R_{0,\theta }(p)={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{bmatrix}}{\begin{bmatrix}p_{x}\\p_{y}\end{bmatrix}}.}$$

Estas matrices son las matrices ortogonales (es decir, cada una es una matriz cuadrada G cuya transpuesta es su inversa , es decir ), con determinante 1 (la otra posibilidad para matrices ortogonales es −1, que da una imagen especular, véase más abajo). Forman el grupo ortogonal especial SO(2). ${\displaystyle GG^{T}=G^{T}G=I_{2}.}$

Se puede lograr una rotación alrededor de c trasladando primero c al origen, luego realizando la rotación alrededor del origen y finalmente trasladando el origen nuevamente a c . Es decir,

$${\displaystyle R_{c,\theta }=T_{c}\circ R_{0,\theta }\circ T_{-c},}$$

o en otras palabras,

$${\displaystyle R_{c,\theta }(p)=c+R_{0,\theta }(p-c).}$$

Alternativamente, se realiza una rotación alrededor del origen, seguida de una traslación:

$${\displaystyle R_{c,\theta }(p)=c-R_{0,\theta }c+R_{0,\theta }(p).}$$

Una rotación puede verse como una composición de dos reflexiones no paralelas.

Transformaciones rígidas

El conjunto de traslaciones y rotaciones forman en conjunto los movimientos rígidos o desplazamientos rígidos . Este conjunto forma un grupo bajo composición, el grupo de los movimientos rígidos , un subgrupo del grupo completo de isometrías euclidianas.

Reflexiones de deslizamiento

Reflexión de deslizamiento

Las reflexiones de deslizamiento , denotadas por G _{c , v , w} , donde c es un punto en el plano, v es un vector unitario en R ² y w es un vector no nulo perpendicular a v son una combinación de una reflexión en la línea descrita por c y v , seguida de una traslación a lo largo de w . Es decir,

$${\displaystyle G_{c,v,w}=T_{w}\circ F_{c,v},}$$

o en otras palabras,

$${\displaystyle G_{c,v,w}(p)=w+F_{c,v}(p).}$$

(También es cierto que

$${\displaystyle G_{c,v,w}(p)=F_{c,v}(p+w);}$$

es decir, obtenemos el mismo resultado si hacemos la traslación y la reflexión en orden opuesto.)

Alternativamente, multiplicamos por una matriz ortogonal con determinante −1 (que corresponde a una reflexión en una línea que pasa por el origen), seguida de una traslación. Esta es una reflexión por deslizamiento, excepto en el caso especial de que la traslación sea perpendicular a la línea de reflexión, en cuyo caso la combinación es en sí misma simplemente una reflexión en una línea paralela.

La isometría identidad , definida por I ( p ) = p para todos los puntos p , es un caso especial de traslación y también de rotación. Es la única isometría que pertenece a más de uno de los tipos descritos anteriormente.

En todos los casos multiplicamos el vector de posición por una matriz ortogonal y sumamos un vector; si el determinante es 1 tenemos una rotación, una traslación o la identidad, y si es −1 tenemos una reflexión de deslizamiento o una reflexión.

Una isometría "aleatoria", como tomar una hoja de papel de una mesa y colocarla al azar, " casi con toda seguridad " es una rotación o una reflexión deslizante (tienen tres grados de libertad ). Esto se aplica independientemente de los detalles de la distribución de probabilidad , siempre que θ y la dirección del vector añadido sean independientes y se distribuyan uniformemente y la longitud del vector añadido tenga una distribución continua. Una traslación pura y una reflexión pura son casos especiales con solo dos grados de libertad, mientras que la identidad es aún más especial, sin grados de libertad.

Isometrías como grupo de reflexión

Las reflexiones, o isometrías especulares, se pueden combinar para producir cualquier isometría. Por lo tanto, las isometrías son un ejemplo de un grupo de reflexión .

Combinaciones de espejos

En el plano euclidiano tenemos las siguientes posibilidades.

Isometrías como espejos

• [ d  ] Identidad

Dos reflejos en el mismo espejo devuelven cada punto a su posición original. Todos los puntos quedan fijos. Cualquier par de espejos idénticos tiene el mismo efecto.

• [ d b ] Reflexión

Como descubrió Alicia a través del espejo , un solo espejo hace que las manos izquierda y derecha se alternen (en términos formales, la orientación topológica se invierte). Los puntos del espejo quedan fijos. Cada espejo tiene un efecto único.

• [ d p ] Rotación

Dos espejos distintos que se intersecan tienen un único punto en común, que permanece fijo. Todos los demás puntos giran alrededor de él formando un ángulo que es el doble del que forman los espejos. Dos espejos cualesquiera que tengan el mismo punto fijo y el mismo ángulo producen la misma rotación, siempre que se utilicen en el orden correcto.

• [ d d ] Traducción

Dos espejos distintos que no se intersecan deben ser paralelos. Cada punto se mueve la misma distancia, el doble de la distancia entre los espejos, y en la misma dirección. Ningún punto queda fijo. Cualquier par de espejos con la misma dirección paralela y la misma distancia entre sí dan la misma traslación, siempre que se utilicen en el orden correcto.

• [ d q ] Reflexión de deslizamiento

Tres espejos. Si todos son paralelos, el efecto es el mismo que con un solo espejo (deslizar un par para cancelar el tercero). De lo contrario, podemos encontrar una disposición equivalente donde dos son paralelos y el tercero es perpendicular a ellos. El efecto es una reflexión combinada con una traslación paralela al espejo. No se deja ningún punto fijo.

Tres espejos son suficientes

Añadir más espejos no añade más posibilidades (en el plano), porque siempre se pueden reorganizar para provocar una cancelación.

Prueba

Una isometría está completamente determinada por su efecto sobre tres puntos independientes (no colineales). Supongamos que p ₁ , p ₂ , p ₃ se asignan a q ₁ , q ₂ , q ₃ ; podemos generar una secuencia de espejos para lograr esto de la siguiente manera. Si p ₁ y q ₁ son distintos, elija su bisectriz perpendicular como espejo. Ahora p ₁ se asigna a q ₁ ; y pasaremos todos los espejos posteriores a través de q ₁ , dejándolo fijo. Llamemos a las imágenes de p ₂ y p ₃ bajo esta reflexión p ₂ ′ y p ₃ ′. Si q ₂ es distinto de p ₂ ′, bisectremos el ángulo en q ₁ con un nuevo espejo. Con p ₁ y p ₂ ahora en su lugar, p ₃ está en p ₃ ″; y si no está en su lugar, un espejo final a través de q ₁ y q ₂ lo volteará a q ₃ . Por lo tanto, como máximo tres reflexiones son suficientes para reproducir cualquier isometría plana. QED

Reconocimiento

Podemos reconocer cuál de estas isometrías tenemos según conserve las manos o las intercambie, y tenga al menos un punto fijo o no, como se muestra en la siguiente tabla (omitiendo la identidad).

Estructura del grupo

Las isometrías que requieren un número impar de espejos (reflexión y reflexión por deslizamiento) siempre se invierten a la izquierda y a la derecha. Las isometrías pares (identidad, rotación y traslación) nunca lo hacen; corresponden a movimientos rígidos y forman un subgrupo normal del grupo euclidiano completo de isometrías. Ni el grupo completo ni el subgrupo par son abelianos ; por ejemplo, invertir el orden de composición de dos espejos paralelos invierte la dirección de la traslación que producen.

Prueba

La identidad es una isometría; nada cambia, por lo tanto la distancia no puede cambiar. Y si una isometría no puede cambiar la distancia, tampoco pueden hacerlo dos (o tres, o más) en sucesión; por lo tanto, la composición de dos isometrías es nuevamente una isometría, y el conjunto de isometrías está cerrado bajo la composición. La isometría identidad también es una identidad para la composición, y la composición es asociativa ; por lo tanto, las isometrías satisfacen los axiomas para un semigrupo . Para un grupo , también debemos tener una inversa para cada elemento. Para cancelar una reflexión, simplemente la componemos consigo misma (Las reflexiones son involuciones ). Y como cada isometría puede expresarse como una secuencia de reflexiones, su inversa puede expresarse como esa secuencia invertida. Nótese que la cancelación de un par de reflexiones idénticas reduce el número de reflexiones en un número par, preservando la paridad de la secuencia; nótese también que la identidad tiene paridad par. Por lo tanto, todas las isometrías forman un grupo, y las isometrías pares un subgrupo. (Las isometrías impares no incluyen la identidad, por lo que no son un subgrupo). Este subgrupo es un subgrupo normal, porque al intercalar una isometría par entre dos impares se obtiene una isometría par. QED

Como el subgrupo par es normal, es el núcleo de un homomorfismo a un grupo cociente , donde el cociente es isomorfo a un grupo formado por una reflexión y la identidad. Sin embargo, el grupo completo no es un producto directo , sino solo un producto semidirecto , del subgrupo par y el grupo cociente.

Composición

La composición de isometrías mezcla tipos de diversas maneras. Podemos pensar en la identidad como dos espejos o ninguno; en cualquier caso, no tiene efecto en la composición. Y dos reflexiones dan una traslación o una rotación, o la identidad (que es ambas, de manera trivial). La reflexión compuesta con cualquiera de estas dos podría cancelarse hasta una sola reflexión; de lo contrario, da la única isometría de tres espejos disponible, una reflexión de deslizamiento. Un par de traslaciones siempre se reduce a una sola traslación; por lo que los casos desafiantes involucran rotaciones. Sabemos que una rotación compuesta ya sea con una rotación o una traslación debe producir una isometría par. La composición con traslación produce otra rotación (en la misma cantidad, con un punto fijo desplazado), pero la composición con rotación puede producir una traslación o una rotación. A menudo se dice que la composición de dos rotaciones produce una rotación, y Euler demostró un teorema a tal efecto en 3D; sin embargo, esto solo es cierto para rotaciones que comparten un punto fijo.

Traslación, rotación y subgrupos ortogonales

De este modo, tenemos dos nuevos tipos de subgrupos de isometrías: todas las traslaciones y las rotaciones que comparten un punto fijo. Ambos son subgrupos del subgrupo par, dentro del cual las traslaciones son normales. Como las traslaciones son un subgrupo normal, podemos factorizarlas y dejar el subgrupo de isometrías con un punto fijo, el grupo ortogonal .

Adición de traducción con espejos

Prueba

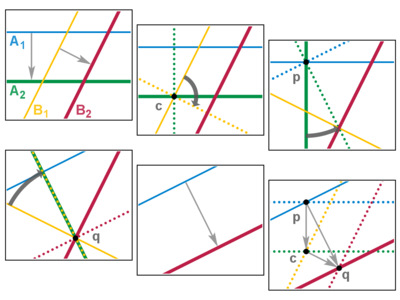
Si dos rotaciones comparten un punto fijo, entonces podemos girar el par de espejos de la segunda rotación para cancelar los espejos internos de la secuencia de cuatro (dos y dos), dejando solo el par externo. De esta manera, la composición de dos rotaciones con un punto fijo común produce una rotación por la suma de los ángulos alrededor del mismo punto fijo.

Si dos traslaciones son paralelas, podemos deslizar el par de espejos de la segunda traslación para cancelar el espejo interior de la secuencia de cuatro, de forma muy similar a lo que ocurre en el caso de la rotación. De este modo, la composición de dos traslaciones paralelas produce una traslación por la suma de las distancias en la misma dirección. Ahora supongamos que las traslaciones no son paralelas y que la secuencia de espejos es A ₁ , A ₂ (la primera traslación) seguida de B ₁ , B ₂ (la segunda). Entonces A ₂ y B ₁ deben cruzarse, digamos en c ; y, reasociando, somos libres de hacer pivotar este par interior alrededor de c . Si giramos 90°, sucede algo interesante: ahora A ₁ y A ₂ ′ se intersecan en un ángulo de 90°, digamos en p , y lo mismo hacen B ₁ ′ y B ₂ , digamos en q . Nuevamente reasociando, giramos el primer par alrededor de p para hacer que B ₂ ″ pase por q , y giramos el segundo par alrededor de q para hacer que A ₁ ″ pase por p . Los espejos interiores coinciden y se cancelan, y los espejos exteriores quedan paralelos. Por lo tanto, la composición de dos traslaciones no paralelas también produce una traslación. Además, los tres puntos de pivote forman un triángulo cuyos bordes dan la regla de suma de vectores : 2( p c ) + 2( c q ) = 2( p q ) . QED

Construcción de grupos anidados

La estructura del subgrupo sugiere otra forma de componer una isometría arbitraria:

Elija un punto fijo y un espejo que pase por él.

1. Si la isometría es impar, utilice el espejo; de lo contrario, no lo haga.
2. Si es necesario, gire alrededor del punto fijo.
3. Si es necesario, traduzca.

Esto funciona porque las traslaciones son un subgrupo normal del grupo completo de isometrías, con cociente del grupo ortogonal; y las rotaciones alrededor de un punto fijo son un subgrupo normal del grupo ortogonal, con cociente de una sola reflexión.

Subgrupos discretos

Grupo diedro de simetrías de pentágonos regulares

Los subgrupos discutidos hasta ahora no sólo son infinitos, sino que también son continuos ( grupos de Lie ). Cualquier subgrupo que contenga al menos una traslación distinta de cero debe ser infinito, pero los subgrupos del grupo ortogonal pueden ser finitos. Por ejemplo, las simetrías de un pentágono regular consisten en rotaciones por múltiplos enteros de 72° (360° / 5), junto con reflexiones en los cinco espejos que bisecan perpendicularmente las aristas. Este es un grupo, D ₅ , con 10 elementos. Tiene un subgrupo, C ₅ , de la mitad del tamaño, omitiendo las reflexiones. Estos dos grupos son miembros de dos familias, D _n y C _n , para cualquier n > 1. Juntas, estas familias constituyen los grupos roseta .

Las traslaciones no se pliegan sobre sí mismas, pero podemos tomar múltiplos enteros de cualquier traslación finita, o sumas de múltiplos de dos de esas traslaciones independientes, como un subgrupo. Estos generan la red de un teselado periódico del plano.

También podemos combinar estos dos tipos de grupos discretos (las rotaciones y reflexiones discretas alrededor de un punto fijo y las traslaciones discretas) para generar los grupos de frisos y los grupos de papel tapiz . Curiosamente, solo unos pocos de los grupos de punto fijo son compatibles con las traslaciones discretas. De hecho, la compatibilidad reticular impone una restricción tan severa que, hasta el isomorfismo , solo tenemos 7 grupos de frisos distintos y 17 grupos de papel tapiz distintos. Por ejemplo, las simetrías del pentágono, D ₅ , son incompatibles con una red discreta de traslaciones. (Cada dimensión superior también tiene solo un número finito de tales grupos cristalográficos , pero el número crece rápidamente; por ejemplo, 3D tiene 230 grupos y 4D tiene 4783).

Isometrías en el plano complejo

En términos de números complejos , las isometrías del plano son de la forma

$${\displaystyle {\begin{array}{ccc}\mathbb {C} &\longrightarrow &\mathbb {C} \\z&\mapsto &a+\omega z\end{array}}}$$

o de la forma

$${\displaystyle {\begin{array}{ccc}\mathbb {C} &\longrightarrow &\mathbb {C} \\z&\mapsto &a+\omega {\overline {z}}{\mbox{,}}\end{array}}}$$

para algunos números complejos a y ω con |ω| = 1. Esto es fácil de demostrar: si a = f (0) y ω = f (1) − f (0) y si uno define

$${\displaystyle {\begin{array}{rccc}g\colon &\mathbb {C} &\longrightarrow &\mathbb {C} \\&z&\mapsto &{\frac {f(z)-a}{\omega }}{\mbox{,}}\end{array}}}$$

entonces g es una isometría, g (0) = 0 , y g (1) = 1 . Es fácil ver entonces que g es la identidad o la conjugación, y la afirmación que se está demostrando se sigue de esto y del hecho de que f ( z ) = a + ωg ( z ) .

Obviamente esto está relacionado con la clasificación anterior de isometrías planas, ya que:

• Las funciones del tipo z → a + z son traslaciones;
• Las funciones del tipo z → ω z son rotaciones (cuando |ω| = 1);
• La conjugación es una reflexión.

Nótese que una rotación alrededor del punto complejo p se obtiene mediante aritmética compleja con

$${\displaystyle z\mapsto \omega (z-p)+p=\omega z+p(1-\omega )}$$

donde la última expresión muestra la aplicación equivalente a la rotación en 0 y una traslación. Por lo tanto, dada la isometría directa se puede resolver para obtener como el centro para una rotación equivalente, siempre que , es decir, siempre que la isometría directa no sea una traslación pura. Como afirma Cederberg, "Una isometría directa es una rotación o una traslación". ^[1] ${\displaystyle z\mapsto \omega z+a,}$ ${\displaystyle p(1-\omega )=a}$ ${\displaystyle p=a/(1-\omega )}$ ${\displaystyle \omega \neq 1}$

Véase también

• Teorema de Beckman-Quarles , una caracterización de las isometrías como las transformaciones que preservan las distancias unitarias
• Congruencia (geometría)
• Rotaciones y reflexiones de coordenadas
• Teorema de Hjelmslev , afirmación de que los puntos medios de pares de puntos correspondientes en una isometría de líneas son colineales.

Referencias

1. Cederberg, Judith N. (2001). Un curso de geometría moderna . Springer. Págs. 136-164. ISBN. 978-0-387-98972-3., cita de la página 151

Enlaces externos

• Isometrías planas