Estimación de intervalos

Intervalo delimitado por una estadística de límite superior e inferior

En estadística , la estimación de intervalos es el uso de datos de muestra para estimar un intervalo de posibles valores de un parámetro de interés. Esto contrasta con la estimación puntual , que proporciona un único valor. ^[1]

Las formas más frecuentes de estimación de intervalos son los intervalos de confianza ( un método frecuentista ) y los intervalos creíbles (un método bayesiano ). ^[2] Las formas menos comunes incluyen intervalos de verosimilitud , intervalos fiduciales , intervalos de tolerancia e intervalos de predicción . Para un método no estadístico, las estimaciones de intervalos se pueden deducir a partir de la lógica difusa .

Tipos

Intervalos de confianza

Los intervalos de confianza se utilizan para estimar el parámetro de interés a partir de un conjunto de datos muestreados, comúnmente la media o la desviación estándar . Un intervalo de confianza indica que hay un 100γ% de confianza en que el parámetro de interés se encuentra dentro de un límite inferior y superior. Un error común en los intervalos de confianza es que el 100γ% del conjunto de datos se encuentra dentro o por encima/debajo de los límites; esto se conoce como intervalo de tolerancia, que se analiza a continuación.

Existen múltiples métodos utilizados para construir un intervalo de confianza, la elección correcta depende de los datos que se analizan. Para una distribución normal con una varianza conocida , se utiliza la tabla z para crear un intervalo donde se puede obtener un nivel de confianza del 100γ% centrado alrededor de la media de la muestra de un conjunto de datos de n mediciones, . Para una distribución binomial , los intervalos de confianza se pueden aproximar utilizando el método aproximado de Wald , el intervalo de Jeffreys y el intervalo de Clopper-Pearson . El método de Jeffrey también se puede utilizar para aproximar intervalos para una distribución de Poisson . ^[3] Si se desconoce la distribución subyacente, se puede utilizar el bootstrap para crear límites sobre la mediana del conjunto de datos.

Intervalos creíbles

Distribución bayesiana: ajuste de una distribución previa para formar una probabilidad posterior.

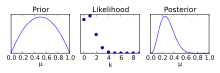
A diferencia de un intervalo de confianza, un intervalo creíble requiere una suposición previa , modificando la suposición utilizando un factor de Bayes y determinando una distribución posterior . Utilizando la distribución posterior, se puede determinar una probabilidad del 100γ% de que el parámetro de interés esté incluido, a diferencia del intervalo de confianza donde se puede tener una confianza del 100γ% de que una estimación está incluida dentro de un intervalo. ^[4]

${\displaystyle {\text{Posterior}}\ \propto \ {\text{Likelihood}}\times {\text{Prior}}}$

Si bien una suposición previa es útil para proporcionar más datos para construir un intervalo, elimina la objetividad de un intervalo de confianza. Se utilizará una suposición previa para informar una suposición posterior; si no se la cuestiona, esta suposición previa puede conducir a predicciones incorrectas. ^[5]

Los límites del intervalo creíble son variables, a diferencia del intervalo de confianza. Existen múltiples métodos para determinar dónde se deben ubicar los límites superior e inferior correctos. Las técnicas comunes para ajustar los límites del intervalo incluyen el intervalo de densidad posterior más alto (HPDI), el intervalo de colas iguales o la elección del centro del intervalo alrededor de la media.

Formas menos comunes

Basado en probabilidad

Utiliza los principios de una función de verosimilitud para estimar el parámetro de interés. Utilizando el método basado en verosimilitud, se pueden encontrar intervalos de confianza para medias exponenciales, de Weibull y lognormales. Además, los enfoques basados ​​en verosimilitud pueden proporcionar intervalos de confianza para la desviación estándar. También es posible crear un intervalo de predicción combinando la función de verosimilitud y la variable aleatoria futura. ^[3]

Fiducial

La inferencia fiducial utiliza un conjunto de datos, elimina cuidadosamente el ruido y recupera un estimador de distribución, la Distribución Fiducial Generalizada (GFD). Sin el uso del Teorema de Bayes, no hay suposición de un previo, al igual que los intervalos de confianza. La inferencia fiducial es una forma menos común de inferencia estadística . El fundador, RA Fisher , que había estado desarrollando métodos de probabilidad inversa, tenía sus propias preguntas sobre la validez del proceso. Si bien la inferencia fiducial se desarrolló a principios del siglo XX, a fines del siglo XX se creía que el método era inferior a los enfoques frecuentistas y bayesianos, pero tenía un lugar importante en el contexto histórico para la inferencia estadística. Sin embargo, los enfoques modernos han generalizado el intervalo fiducial en la Inferencia Fiducial Generalizada (GFI), que se puede utilizar para estimar conjuntos de datos discretos y continuos. ^[6]

Tolerancia

Los intervalos de tolerancia utilizan la población de un conjunto de datos recopilados para obtener un intervalo, dentro de los límites de tolerancia, que contiene valores del 100γ%. Los ejemplos que se utilizan normalmente para describir los intervalos de tolerancia incluyen la fabricación. En este contexto, se evalúa un porcentaje de un conjunto de productos existente para garantizar que un porcentaje de la población esté incluido dentro de los límites de tolerancia. Al crear intervalos de tolerancia, los límites se pueden escribir en términos de un límite de tolerancia superior e inferior, utilizando la media de la muestra , y la desviación estándar de la muestra , . ${\displaystyle \mu }$

${\displaystyle (l_{b},u_{b})=\mu \pm k_{2}s}$para intervalos de dos lados

para intervalos de dos lados

Y en el caso de intervalos unilaterales donde la tolerancia se requiere sólo por encima o por debajo de un valor crítico,

${\displaystyle l_{b}=\mu -k_{1}s}$

${\displaystyle u_{b}=\mu +k_{1}s}$

${\displaystyle k_{i}}$Varía según la distribución y el número de lados, i, en la estimación del intervalo. En una distribución normal,  se puede expresar como ^[7] ${\displaystyle k_{2}}$

${\displaystyle k_{2}=z_{\alpha /2}{\sqrt {\frac {\nu (1+{\frac {1}{N}})}{\chi _{1-\alpha ,\nu }^{2}}}}}$

Dónde,

${\displaystyle \chi _{1-\alpha ,\nu }^{2}}$es el valor crítico de la distribución de chi-cuadrado que utiliza grados de libertad que se excede con probabilidad . ${\displaystyle \nu }$ ${\displaystyle \alpha }$

${\displaystyle z_{\alpha /2}}$son los valores críticos obtenidos de la distribución normal.

Predicción

Un intervalo de predicción estima el intervalo que contiene muestras futuras con cierta confianza, γ. Los intervalos de predicción se pueden utilizar tanto en contextos bayesianos como frecuentistas . Estos intervalos se utilizan normalmente en conjuntos de datos de regresión, pero no se utilizan para la extrapolación más allá de los parámetros controlados experimentalmente de los datos anteriores. ^[8]

Lógica difusa

La lógica difusa se utiliza para gestionar la toma de decisiones de forma no binaria en el ámbito de la inteligencia artificial, las decisiones médicas y otros campos. En general, toma datos de entrada, los mapea a través de sistemas de inferencia difusa y produce una decisión de salida. Este proceso implica fuzzificación, evaluación de reglas de lógica difusa y desfuzzificación. Al analizar la evaluación de reglas de lógica difusa, las funciones de pertenencia convierten nuestra información de entrada no binaria en variables tangibles. Estas funciones de pertenencia son esenciales para predecir la incertidumbre del sistema.

Unilateral vs. bilateral

Diferenciar entre intervalos bilaterales y unilaterales en una curva de distribución normal estándar.

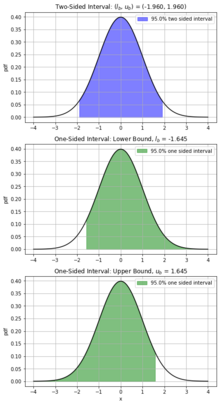
Los intervalos bilaterales estiman un parámetro de interés, Θ, con un nivel de confianza, γ, utilizando un límite inferior ( ) y un límite superior ( ). Algunos ejemplos pueden incluir la estimación de la altura promedio de los hombres en una región geográfica o las longitudes de un escritorio en particular fabricado por un fabricante. Estos casos tienden a estimar el valor central de un parámetro. Por lo general, esto se presenta en una forma similar a la ecuación siguiente. ${\displaystyle l_{b}}$ ${\displaystyle u_{b}}$

${\displaystyle P(l_{b}<\Theta <u_{b})=\gamma }$

A diferencia del intervalo bilateral, el intervalo unilateral utiliza un nivel de confianza, γ, para construir un límite mínimo o máximo que predice el parámetro de interés con una probabilidad de γ*100 %. Normalmente, se requiere un intervalo unilateral cuando el límite mínimo o máximo de la estimación no es de interés. Cuando se trata del valor mínimo predicho de Θ, ya no es necesario encontrar límites superiores de la estimación, lo que conduce a una forma reducida del intervalo bilateral.

${\displaystyle P(l_{b}<\Theta )=\gamma }$

Como resultado de eliminar el límite superior y mantener la confianza, el límite inferior ( ) aumentará. Del mismo modo, cuando se trata de encontrar solo un límite superior de la estimación de un parámetro, el límite superior disminuirá. Un intervalo unilateral es un parámetro que se encuentra comúnmente en el control de calidad de la producción de materiales , donde un valor esperado de la resistencia de un material, Θ, debe ser superior a un cierto valor mínimo ( ) con cierta confianza (100γ%). En este caso, el fabricante no está preocupado por producir un producto que sea demasiado fuerte, no hay límite superior ( ). ${\displaystyle l_{b}}$ ${\displaystyle l_{b}}$ ${\displaystyle u_{b}}$

Discusión

Al determinar la significancia estadística de un parámetro, es mejor comprender los datos y sus métodos de recolección. Antes de recolectar datos, se debe planificar un experimento de manera que el error de muestreo sea una variabilidad estadística (un error aleatorio ), en lugar de un sesgo estadístico (un error sistemático ). ^[9] Después de experimentar, un primer paso típico para crear estimaciones de intervalo es el análisis exploratorio que se realiza mediante varios métodos gráficos . A partir de esto, se puede determinar la distribución de muestras del conjunto de datos. Producir límites de intervalo con suposiciones incorrectas basadas en la distribución hace que una predicción sea defectuosa. ^[10]

Cuando se informan estimaciones de intervalos, deben tener una interpretación común dentro y fuera de la comunidad científica. Las estimaciones de intervalos derivadas de la lógica difusa tienen significados mucho más específicos de la aplicación.

En situaciones que ocurren con frecuencia, debe haber conjuntos de procedimientos estándar que se puedan utilizar, sujetos a la verificación y validez de los supuestos requeridos. Esto se aplica tanto a los intervalos de confianza como a los intervalos creíbles. Sin embargo, en situaciones más novedosas, debe haber una guía sobre cómo se pueden formular estimaciones de intervalos. En este sentido, los intervalos de confianza y los intervalos creíbles tienen una posición similar, pero hay dos diferencias. En primer lugar, los intervalos creíbles pueden manejar fácilmente la información previa, mientras que los intervalos de confianza no pueden. En segundo lugar, los intervalos de confianza son más flexibles y se pueden usar prácticamente en más situaciones que los intervalos creíbles: un área en la que los intervalos creíbles sufren en comparación es en el manejo de modelos no paramétricos .

Debería haber formas de probar el desempeño de los procedimientos de estimación de intervalos. Esto surge porque muchos de estos procedimientos implican aproximaciones de varios tipos y existe la necesidad de verificar que el desempeño real de un procedimiento sea cercano a lo que se afirma. El uso de simulaciones estocásticas hace que esto sea sencillo en el caso de los intervalos de confianza, pero es algo más problemático para los intervalos creíbles en los que es necesario tener en cuenta adecuadamente la información previa. La verificación de intervalos creíbles se puede realizar para situaciones que no representan información previa, pero la verificación implica verificar las propiedades de frecuencia de largo plazo de los procedimientos.

Severini (1993) analiza las condiciones bajo las cuales los intervalos creíbles y los intervalos de confianza producirán resultados similares, y también analiza tanto las probabilidades de cobertura de los intervalos creíbles como las probabilidades posteriores asociadas con los intervalos de confianza. ^[11]

En la teoría de la decisión , que es un enfoque común y una justificación de las estadísticas bayesianas, la estimación de intervalos no es de interés directo. El resultado es una decisión, no una estimación de intervalo, y por lo tanto los teóricos de la decisión bayesiana utilizan una acción bayesiana : minimizan la pérdida esperada de una función de pérdida con respecto a toda la distribución posterior, no a un intervalo específico.

Aplicaciones

Las aplicaciones de los intervalos de confianza se utilizan para resolver una variedad de problemas relacionados con la incertidumbre. Katz (1975) propone varios desafíos y beneficios para utilizar estimaciones de intervalos en procedimientos legales. ^[12] Para su uso en investigación médica, Altmen (1990) analiza el uso de intervalos de confianza y las pautas para su uso. ^[13] En la fabricación, también es común encontrar estimaciones de intervalos que estiman la vida útil de un producto o que evalúan las tolerancias de un producto. Meeker y Escobar (1998) presentan métodos para analizar datos de confiabilidad bajo estimación paramétrica y no paramétrica, incluida la predicción de variables aleatorias futuras (intervalos de predicción). ^[14]

Véase también

• Portal de matemáticas

• Regla 68-95-99,7
• Inferencia algorítmica
• El problema de Behrens-Fisher jugó un papel importante en el desarrollo de la teoría detrás de las metodologías estadísticas aplicables.
• Probabilidad de cobertura
• Estadísticas de estimación
• Inducción (filosofía)
• Margen de error
• Comparaciones múltiples
• Filosofía de la estadística
• Inferencia predictiva
• Interferencia estadística

Referencias

1. Neyman, J. (1937). "Esquema de una teoría de estimación estadística basada en la teoría clásica de la probabilidad". Philosophical Transactions of the Royal Society of London. Serie A, Ciencias matemáticas y físicas . 236 (767). The Royal Society: 333–380. Bibcode :1937RSPTA.236..333N. doi : 10.1098/rsta.1937.0005 . ISSN  0080-4614. JSTOR  91337. S2CID  19584450 . Consultado el 15 de julio de 2021 .
2. Severini, Thomas A. (1991). "Sobre la relación entre estimaciones de intervalo bayesianas y no bayesianas". Revista de la Royal Statistical Society, Serie B (Metodológica) . 53 (3). Wiley: 611–618. doi :10.1111/j.2517-6161.1991.tb01849.x. ISSN  0035-9246.
3. Meeker, William Q.; Hahn, Gerald J.; Escobar, Luis A. (2017-03-27). Intervalos estadísticos: una guía para profesionales e investigadores . Serie Wiley en probabilidad y estadística (1.ª ed.). Wiley. doi :10.1002/9781118594841. ISBN 978-0-471-68717-7.
4. Hespanhol, Luiz; Vallio, Caio Sain; Costa, Lucíola Menezes; Saragiotto, Bruno T (1 de julio de 2019). "Comprensión e interpretación de los intervalos de confianza y credibilidad en torno a las estimaciones de efectos". Revista Brasileña de Fisioterapia . 23 (4): 290–301. doi :10.1016/j.bjpt.2018.12.006. ISSN  1413-3555. PMC 6630113 . PMID  30638956. 
5. Lee, Peter M. (2012). Estadística bayesiana: una introducción (4.ª ed., 1.ª ed. publ.). Chichester: Wiley. ISBN 978-1-118-33257-3.
6. Hannig, Jan; Iyer, Hari; Lai, Randy CS; Lee, Thomas CM (2 de julio de 2016). "Inferencia fiducial generalizada: una revisión y nuevos resultados". Revista de la Asociación Estadounidense de Estadística . 111 (515): 1346–1361. doi :10.1080/01621459.2016.1165102. ISSN  0162-1459.
7. Howe, WG (junio de 1969). "Límites de tolerancia bilaterales para poblaciones normales, algunas mejoras". Revista de la Asociación Estadounidense de Estadística . 64 (326): 610. doi :10.2307/2283644. ISSN  0162-1459.
8. Vardeman, Stephen B. (1992). "¿Qué pasa con los otros intervalos?". The American Statistician . 46 (3): 193–197. doi :10.2307/2685212. ISSN  0003-1305.
9. Hahn, Gerald J.; Meeker, William Q. (1993). "Supuestos para la inferencia estadística". The American Statistician . 47 (1): 1–11. doi :10.2307/2684774. ISSN  0003-1305.
10. Hahn, Gerald J.; Doganaksoy, Necip; Meeker, William Q. (1 de agosto de 2019). "Intervalos estadísticos, no significancia estadística". Significancia . 16 (4): 20–22. doi : 10.1111/j.1740-9713.2019.01298.x . ISSN  1740-9705.
11. Severini, Thomas A. (1993). "Estimaciones de intervalos bayesianos que también son intervalos de confianza". Revista de la Royal Statistical Society. Serie B (Metodológica) . 55 (2): 533–540. ISSN  0035-9246.
12. Katz, Leo (1975). "Presentación de una estimación del intervalo de confianza como prueba en un procedimiento legal". The American Statistician . 29 (4): 138–142. doi :10.2307/2683480. ISSN  0003-1305.
13. Altman, Douglas G., ed. (2011). Estadísticas con confianza: intervalos de confianza y pautas estadísticas; [incluye disco] (2. ed., [Nachdr.] ed.). Londres: BMJ Books. ISBN 978-0-7279-1375-3.
14. Meeker, William Q.; Escobar, Luis A. (1998). Métodos estadísticos para datos de confiabilidad . Series de Wiley en probabilidad y estadística. Sección de probabilidad y estadística aplicada. Nueva York Weinheim: Wiley. ISBN 978-0-471-14328-4.

Bibliografía

• Kendall, MG y Stuart, A. (1973). La teoría avanzada de la estadística. Vol. 2: Inferencia y relación (3.ª edición). Griffin, Londres.

En el capítulo 20 se tratan los intervalos de confianza, mientras que en el capítulo 21 se tratan los intervalos fiduciales y los intervalos bayesianos y se analizan comparativamente los tres enfoques. Cabe señalar que este trabajo es anterior a las metodologías modernas que requieren un uso intensivo de los cálculos. Además, en el capítulo 21 se analiza el problema de Behrens-Fisher.

• Meeker, WQ, Hahn, GJ y Escobar, LA (2017). Intervalos estadísticos: una guía para profesionales e investigadores (segunda edición). John Wiley & Sons.

Enlaces externos

• Introducción a las matemáticas difusas https://web.archive.org/web/20061205114153/http://blog.peltarion.com/2006/10/25/fuzzy-math-part-1-the-theory
• ¿Qué es la lógica difusa? https://www.youtube.com/watch?v=__0nZuG4sTw