En Grupo (matemáticas) se dan algunos ejemplos elementales de grupos en matemáticas . Aquí se enumeran más ejemplos.

Considere tres bloques de colores (rojo, verde y azul), colocados inicialmente en el orden RGB. Sea a la operación "intercambiar el primer bloque y el segundo bloque", y b la operación "intercambiar el segundo bloque y el tercer bloque".
Podemos escribir xy para la operación "primero haz y , luego haz x "; de modo que ab es la operación RGB → RBG → BRG, que podría describirse como "mover los dos primeros bloques una posición a la derecha y poner el tercer bloque en la primera posición". Si escribimos e para "dejar los bloques como están" (la operación de identidad ), entonces podemos escribir las seis permutaciones de los tres bloques de la siguiente manera:
Nótese que aa tiene el efecto RGB → GRB → RGB; por lo que podemos escribir aa = e . De manera similar, bb = ( aba )( aba ) = e ; ( ab )( ba ) = ( ba )( ab ) = e ; por lo que cada elemento tiene una inversa .
Por inspección, podemos determinar la asociatividad y el cierre ; note en particular que ( ba ) b = bab = b ( ab ).
Como se construye a partir de las operaciones básicas a y b , decimos que el conjunto { a , b } genera este grupo. El grupo, llamado grupo simétrico S 3 , tiene orden 6 y es no abeliano (ya que, por ejemplo, ab ≠ ba ).
Una traslación del plano es un movimiento rígido de cada punto del plano durante una cierta distancia en una cierta dirección. Por ejemplo, "moverse en dirección noreste durante 2 kilómetros" es una traslación del plano. Dos traslaciones como a y b se pueden componer para formar una nueva traslación a ∘ b de la siguiente manera: primero siga la prescripción de b , luego la de a . Por ejemplo, si
y
entonces
O si
y
entonces
(ver el teorema de Pitágoras para saber por qué esto es así, geométricamente).
El conjunto de todas las traslaciones del plano con composición como operación forma un grupo:
Éste es un grupo abeliano y nuestro primer ejemplo (no discreto) de un grupo de Lie : un grupo que también es una variedad .


Los grupos son muy importantes para describir la simetría de los objetos, ya sean geométricos (como un tetraedro ) o algebraicos (como un conjunto de ecuaciones). Como ejemplo, consideremos un cuadrado de vidrio de cierto grosor (con una letra "F" escrita sobre él, solo para que se puedan distinguir las diferentes posiciones).
Para describir su simetría, formamos el conjunto de todos aquellos movimientos rígidos del cuadrado que no hacen una diferencia visible (excepto la "F"). Por ejemplo, si un objeto girado 90° en el sentido de las agujas del reloj sigue pareciendo el mismo, el movimiento es un elemento del conjunto, por ejemplo a . También podríamos girarlo sobre un eje vertical de modo que su superficie inferior se convierta en su superficie superior, mientras que el borde izquierdo se convierta en el borde derecho. Nuevamente, después de realizar este movimiento, el cuadrado de vidrio parece el mismo, por lo que este también es un elemento de nuestro conjunto y lo llamamos b . El movimiento que no hace nada se denota por e .
Dados dos movimientos x e y , es posible definir la composición x ∘ y como se indica arriba: primero se realiza el movimiento y , seguido del movimiento x . El resultado dejará la losa con el mismo aspecto que antes.
La cuestión es que el conjunto de todos esos movimientos, cuya operación es la composición, forma un grupo. Este grupo es la descripción más concisa de la simetría del cuadrado. Los químicos utilizan grupos de simetría de este tipo para describir la simetría de cristales y moléculas .
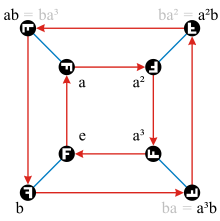
Investiguemos un poco más el grupo de simetría de nuestro cuadrado. Ahora mismo, tenemos los elementos a , b y e , pero podemos formar fácilmente más: por ejemplo, a ∘ a , también escrito como a 2 , es un giro de 180°. a 3 es una rotación de 270° en el sentido de las agujas del reloj (o una rotación de 90° en el sentido contrario a las agujas del reloj). También vemos que b 2 = e y también a 4 = e . Aquí hay una pregunta interesante: ¿qué hace a ∘ b ? Primero se da la vuelta horizontalmente, luego rota. Trata de visualizar que a ∘ b = b ∘ a 3 . Además, a 2 ∘ b es una vuelta vertical y es igual a b ∘ a 2 .
Decimos que los elementos a y b generan el grupo.
Este grupo de orden 8 tiene la siguiente tabla de Cayley :
Para dos elementos cualesquiera del grupo, la tabla registra cuál es su composición. Aquí escribimos " a 3 b " como abreviatura de a 3 ∘ b .
En matemáticas, este grupo se conoce como grupo diedro de orden 8 y se denota como Dih 4 , D 4 o D 8 , según la convención. Este fue un ejemplo de un grupo no abeliano: la operación ∘ aquí no es conmutativa , lo que se puede ver en la tabla; la tabla no es simétrica respecto de la diagonal principal.

Esta versión de la tabla de Cayley muestra que este grupo tiene un subgrupo normal que se muestra con un fondo rojo. En esta tabla, r significa rotaciones y f significa giros. Debido a que el subgrupo es normal, la clase lateral izquierda es la misma que la clase lateral derecha.
El grupo libre con dos generadores a y b consta de todas las cadenas /palabras finitas que se pueden formar a partir de los cuatro símbolos a , a −1 , b y b −1 de manera que no aparezca ningún a directamente junto a un a −1 y ningún b aparezca directamente junto a un b −1 . Dos de estas cadenas se pueden concatenar y convertir en una cadena de este tipo reemplazando repetidamente las subcadenas "prohibidas" con la cadena vacía. Por ejemplo: " abab −1 a −1 " concatenado con " abab −1 a " produce " abab −1 a −1 abab −1 a ", que se reduce a " abaab −1 a ". Se puede comprobar que el conjunto de esas cadenas con esta operación forma un grupo con la cadena vacía ε := "" siendo el elemento identidad (normalmente se omiten las comillas; por eso se requiere el símbolo ε).
Éste es otro grupo infinito no abeliano.
Los grupos libres son importantes en la topología algebraica ; el grupo libre en dos generadores también se utiliza para una prueba de la paradoja de Banach-Tarski .
Sea G un grupo y S un conjunto. El conjunto de aplicaciones M ( S , G ) es en sí mismo un grupo; es decir, para dos aplicaciones f , g de S en G definimos fg como la aplicación tal que ( fg )( x ) = f ( x ) g ( x ) para cada x en S y f −1 como la aplicación tal que f −1 ( x ) = f ( x ) −1 .
Tomemos las funciones f , g y h en M ( S , G ). Para cada x en S , f ( x ) y g ( x ) están ambas en G , y también lo está ( fg )( x ). Por lo tanto, fg también está en M ( S , G ), es decir, M ( S , G ) es cerrado. M ( S , G ) es asociativo porque (( fg ) h )( x ) = ( fg )( x ) h ( x ) = ( f ( x ) g ( x )) h ( x ) = f ( x )( g ( x ) h ( x )) = f ( x )( gh )( x ) = ( f ( gh ))( x ). Y hay una función i tal que i ( x ) = e donde e es el elemento identidad de G . La función i es tal que para todo f en M ( S , G ) tenemos fi = if = f , es decir i es el elemento identidad de M ( S , G ). Por lo tanto, M ( S , G ) es en realidad un grupo.
Si G es abeliano entonces ( fg )( x ) = f ( x ) g ( x ) = g ( x ) f ( x ) = ( gf )( x ), y por lo tanto también lo es M ( S , G ).
Sea G el conjunto de aplicaciones biyectivas de un conjunto S sobre sí mismo. Entonces G forma un grupo bajo la composición ordinaria de aplicaciones. Este grupo se llama grupo simétrico y se denota comúnmente como Σ S o . El elemento identidad de G es la aplicación identidad de S. Para dos aplicaciones f , g en G son biyectivas, fg también es biyectiva. Por lo tanto, G es cerrado. La composición de aplicaciones es asociativa; por lo tanto, G es un grupo. S puede ser finito o infinito .
Si n es un entero positivo , podemos considerar el conjunto de todas las matrices invertibles n por n con componentes de números reales , por ejemplo. Este es un grupo con la multiplicación de matrices como operación. Se llama grupo lineal general y se denota GL n ( R ) o GL( n , R ) (donde R es el conjunto de números reales). Geométricamente, contiene todas las combinaciones de rotaciones, reflexiones, dilataciones y transformaciones oblicuas del espacio euclidiano n -dimensional que fijan un punto dado (el origen).
Si nos limitamos a matrices con determinante 1, obtenemos otro grupo, el grupo lineal especial , SL n ( R ) o SL( n , R ). Geométricamente, este consta de todos los elementos de GL n ( R ) que preservan tanto la orientación como el volumen de los diversos sólidos geométricos en el espacio euclidiano.
Si, en cambio, nos limitamos a las matrices ortogonales , obtenemos el grupo ortogonal O n ( R ) u O( n , R ). Geométricamente, este está formado por todas las combinaciones de rotaciones y reflexiones que fijan el origen. Éstas son precisamente las transformaciones que conservan longitudes y ángulos.
Finalmente, si imponemos ambas restricciones, obtenemos el grupo ortogonal especial SO n ( R ) o SO( n , R ), que consiste únicamente en rotaciones.
Estos grupos son nuestros primeros ejemplos de grupos no abelianos infinitos. Resulta que también son grupos de Lie . De hecho, la mayoría de los grupos de Lie importantes (pero no todos) pueden expresarse como grupos matriciales .
Si esta idea se generaliza a matrices con números complejos como entradas, obtenemos otros grupos de Lie útiles, como el grupo unitario U( n ). También podemos considerar matrices con cuaterniones como entradas; en este caso, no hay una noción bien definida de determinante (y, por lo tanto, no hay una buena manera de definir un "volumen" cuaterniónico), pero aún podemos definir un grupo análogo al grupo ortogonal, el grupo simpléctico Sp( n ).
Además, la idea puede tratarse puramente algebraicamente con matrices sobre cualquier campo , pero entonces los grupos no son grupos de Lie.