Gráfica de rado

Gráfico infinito que contiene todos los gráficos contables

El gráfico de Rado, tal como lo numeraron Ackermann (1937) y Rado (1964).

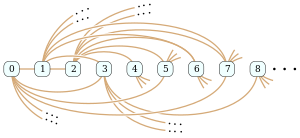
En el campo matemático de la teoría de grafos , el grafo de Rado , grafo de Erdős–Rényi o grafo aleatorio es un grafo infinito numerable que se puede construir (con probabilidad uno ) eligiendo de forma independiente al azar para cada par de sus vértices si conectar los vértices por una arista. Los nombres de este grafo honran a Richard Rado , Paul Erdős y Alfréd Rényi , matemáticos que lo estudiaron a principios de la década de 1960; aparece incluso antes en el trabajo de Wilhelm Ackermann  (1937). El grafo de Rado también se puede construir de forma no aleatoria, simetrizando la relación de pertenencia de los conjuntos finitos hereditarios , aplicando el predicado BIT a las representaciones binarias de los números naturales , o como un grafo de Paley infinito que tiene aristas que conectan pares de números primos congruentes con 1 módulo 4 que son residuos cuadráticos módulo entre sí.

Todo grafo finito o numerablemente infinito es un subgrafo inducido del grafo de Rado, y puede encontrarse como subgrafo inducido mediante un algoritmo voraz que construye el subgrafo vértice por vértice. El grafo de Rado se define de forma única, entre los grafos numerables, por una propiedad de extensión que garantiza la corrección de este algoritmo: no importa qué vértices ya hayan sido elegidos para formar parte del subgrafo inducido, y no importa qué patrón de adyacencias se necesite para extender el subgrafo con un vértice más, siempre existirá otro vértice con ese patrón de adyacencias que el algoritmo voraz puede elegir.

El grafo de Rado es altamente simétrico: cualquier isomorfismo de sus subgrafos inducidos finitos puede extenderse a una simetría de todo el grafo. Las oraciones lógicas de primer orden que son verdaderas para el grafo de Rado también son verdaderas para casi todos los grafos finitos aleatorios, y las oraciones que son falsas para el grafo de Rado también son falsas para casi todos los grafos finitos. En la teoría de modelos , el grafo de Rado es un ejemplo del modelo contable único de una teoría ω-categórica .

Historia

El grafo de Rado fue construido por primera vez por Ackermann (1937) de dos maneras, con vértices ya sean los conjuntos finitos hereditarios o los números naturales. (Estrictamente hablando, Ackermann describió un grafo dirigido , y el grafo de Rado es el grafo no dirigido correspondiente dado al olvidar las direcciones en los bordes). Erdős y Rényi (1963) construyeron el grafo de Rado como el grafo aleatorio en un número contable de puntos. Probaron que tiene infinitos automorfismos, y su argumento también muestra que es único aunque no lo mencionaron explícitamente. Richard Rado  (1964) redescubrió el grafo de Rado como un grafo universal , y dio una construcción explícita del mismo con los números naturales como el conjunto de vértices. La construcción de Rado es esencialmente equivalente a una de las construcciones de Ackermann.

Construcciones

Números binarios

Ackermann (1937) y Rado (1964) construyeron el grafo de Rado utilizando el predicado BIT de la siguiente manera. Identificaron los vértices del grafo con los números naturales 0, 1, 2, ... Una arista conecta los vértices y en el grafo (donde ) siempre que el bit n de la representación binaria de sea distinto de cero. Así, por ejemplo, los vecinos del vértice 0 consisten en todos los vértices impares, porque los números cuyo bit n es distinto de cero son exactamente los números impares. El vértice 1 tiene un vecino más pequeño, el vértice 0, ya que 1 es impar y el vértice 0 está conectado a todos los vértices impares. Los vecinos más grandes del vértice 1 son todos los vértices con números congruentes con 2 o 3 módulo 4, porque esos son exactamente los números con un bit distinto de cero en el índice 1. ^[1] ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle x<y}$ ${\displaystyle x}$ ${\displaystyle y}$

Gráfico aleatorio

El grafo de Rado surge casi con seguridad en el modelo de Erdős–Rényi de un grafo aleatorio con un número contable de vértices. En concreto, se puede formar un grafo infinito eligiendo, de forma independiente y con una probabilidad de 1/2 para cada par de vértices, si se conectan los dos vértices mediante una arista. Con una probabilidad de 1, el grafo resultante es isomorfo al grafo de Rado. Esta construcción también funciona si se utiliza cualquier probabilidad fija distinta de 0 o 1 en lugar de 1/2. ^[2] ${\displaystyle p}$

Este resultado, demostrado por Paul Erdős y Alfréd Rényi  (1963), justifica el artículo definido en el nombre alternativo común " el grafo aleatorio" para el grafo de Rado. Dibujar repetidamente un grafo finito a partir del modelo de Erdős-Rényi conducirá en general a diferentes grafos; sin embargo, cuando se aplica a un grafo infinito numerable, el modelo casi siempre produce el mismo grafo infinito. ^[3]

Para cualquier grafo generado aleatoriamente de esta manera, el grafo complementario puede obtenerse al mismo tiempo invirtiendo todas las opciones: incluyendo una arista cuando el primer grafo no incluía la misma arista, y viceversa. Esta construcción del grafo complementario es una instancia del mismo proceso de elección aleatoria e independiente de si incluir o no cada arista, por lo que también (con probabilidad 1) genera el grafo de Rado. Por lo tanto, el grafo de Rado es un grafo autocomplementario . ^[4]

Otras construcciones

En una de las construcciones originales de Ackermann de 1937, los vértices del grafo de Rado están indexados por los conjuntos finitos hereditarios, y hay una arista entre dos vértices exactamente cuando uno de los conjuntos finitos correspondientes es miembro del otro. Una construcción similar puede basarse en la paradoja de Skolem , el hecho de que existe un modelo contable para la teoría de conjuntos de primer orden. Se puede construir el grafo de Rado a partir de dicho modelo creando un vértice para cada conjunto, con una arista que conecta cada par de conjuntos donde un conjunto en el par es miembro del otro. ^[5]

El grafo de Rado también puede formarse mediante una construcción similar a la de los grafos de Paley , tomando como vértices de un grafo todos los números primos que son congruentes con 1 módulo 4, y conectando dos vértices por una arista siempre que uno de los dos números sea un residuo cuadrático módulo el otro. Por reciprocidad cuadrática y la restricción de los vértices a primos congruentes con 1 módulo 4, esta es una relación simétrica , por lo que define un grafo no dirigido, que resulta ser isomorfo al grafo de Rado. ^[6]

Otra construcción del grafo de Rado muestra que se trata de un grafo circulante infinito , con los números enteros como sus vértices y con una arista entre cada dos números enteros cuya distancia (el valor absoluto de su diferencia) pertenece a un conjunto particular . Para construir el grafo de Rado de esta manera, se puede elegir aleatoriamente, o bien eligiendo la función indicadora de como la concatenación de todas las secuencias binarias finitas . ^[7] ${\displaystyle S}$ ${\displaystyle S}$ ${\displaystyle S}$

El gráfico de Rado también se puede construir como el gráfico de intersección de bloques de un diseño de bloques infinitos en el que el número de puntos y el tamaño de cada bloque son infinitos contablemente . ^[8] También se puede construir como el límite de Fraïssé de la clase de gráficos finitos. ^[9]

Propiedades

Extensión

La propiedad de extensión del gráfico de Rado: para cada dos conjuntos finitos disjuntos de vértices y , existe otro vértice conectado a todo en , y a nada en ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle x}$ ${\displaystyle U}$ ${\displaystyle V}$

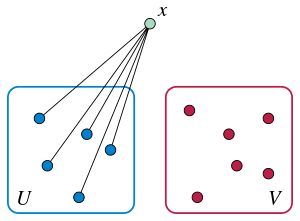
El grafo de Rado satisface la siguiente propiedad de extensión: para cada dos conjuntos finitos disjuntos de vértices y , existe un vértice fuera de ambos conjuntos que está conectado a todos los vértices en , pero no tiene vecinos en . ^[2] Por ejemplo, con la definición de número binario del grafo de Rado, sea Entonces los bits distintos de cero en la representación binaria de hacen que sea adyacente a todo en . Sin embargo, no tiene bits distintos de cero en su representación binaria correspondientes a vértices en , y es tan grande que el bit n de cada elemento de es cero. Por lo tanto, no es adyacente a ningún vértice en . ^[10] ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle x}$ ${\displaystyle U}$ ${\displaystyle V}$ $${\displaystyle x=2^{1+\max(U\cup V)}+\sum _{u\in U}2^{u}.}$$ ${\displaystyle x}$ ${\displaystyle U}$ ${\displaystyle x}$ ${\displaystyle V}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle V}$ ${\displaystyle x}$ ${\displaystyle V}$

Con la definición de grafo aleatorio del grafo de Rado, cada vértice fuera de la unión de y tiene probabilidad de cumplir la propiedad de extensión, independientemente de los otros vértices. Debido a que hay infinitos vértices para elegir, cada uno con la misma probabilidad finita de éxito, la probabilidad es uno de que exista un vértice que cumpla la propiedad de extensión. ^[2] Con la definición de grafo de Paley, para cualesquiera conjuntos y , por el teorema del resto chino , los números que son residuos cuadráticos módulo cada primo en y no residuos módulo cada primo en forman una secuencia periódica, por lo que por el teorema de Dirichlet sobre primos en progresiones aritméticas este grafo de teoría de números tiene la propiedad de extensión. ^[6] ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle 1/2^{|U|+|V|}}$ ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle U}$ ${\displaystyle V}$

Subgrafos inducidos

La propiedad de extensión se puede utilizar para construir copias isomorfas de cualquier grafo finito o infinito numerable dentro del grafo de Rado, como subgrafos inducidos . Para ello, ordene los vértices de , y añada vértices en el mismo orden a una copia parcial de dentro del grafo de Rado. En cada paso, el siguiente vértice en será adyacente a algún conjunto de vértices en que son anteriores en el orden de los vértices, y no adyacente al conjunto restante de vértices anteriores en . Por la propiedad de extensión, el grafo de Rado también tendrá un vértice que es adyacente a todos los vértices en la copia parcial que corresponden a miembros de , y no adyacente a todos los vértices en la copia parcial que corresponden a miembros de . Añadir a la copia parcial de produce una copia parcial más grande, con un vértice más. ^[11] ${\displaystyle G}$ ${\displaystyle G}$ ${\displaystyle G}$ ${\displaystyle G}$ ${\displaystyle U}$ ${\displaystyle G}$ ${\displaystyle V}$ ${\displaystyle G}$ ${\displaystyle x}$ ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle x}$ ${\displaystyle G}$

Este método constituye la base para una prueba por inducción , con el subgrafo de vértice 0 como caso base, de que todo grafo finito o infinito contable es un subgrafo inducido del grafo de Rado. ^[11]

Unicidad

El grafo de Rado es, hasta el isomorfismo de grafos , el único grafo contable con la propiedad de extensión. Por ejemplo, sean y dos grafos contables con la propiedad de extensión, sean y subgrafos inducidos finitos isomorfos de y respectivamente, y sean y los primeros vértices en una enumeración de los vértices de y respectivamente que no pertenecen a y . Luego, al aplicar la propiedad de extensión dos veces, uno puede encontrar subgrafos inducidos isomorfos y que incluyen a y junto con todos los vértices de los subgrafos anteriores. Al repetir este proceso, uno puede construir una secuencia de isomorfismos entre subgrafos inducidos que eventualmente incluya cada vértice en y . Por lo tanto, por el método de ida y vuelta , y deben ser isomorfos. ^[12] Debido a que los grafos construidos por la construcción de grafos aleatorios, la construcción de números binarios y la construcción de grafos de Paley son todos grafos contables con la propiedad de extensión, este argumento muestra que todos son isomorfos entre sí. ^[13] ${\displaystyle G}$ ${\displaystyle H}$ ${\displaystyle G_{i}}$ ${\displaystyle H_{i}}$ ${\displaystyle G}$ ${\displaystyle H}$ ${\displaystyle g_{i}}$ ${\displaystyle h_{i}}$ ${\displaystyle G}$ ${\displaystyle H}$ ${\displaystyle G_{i}}$ ${\displaystyle H_{i}}$ ${\displaystyle G_{i+1}}$ ${\displaystyle H_{i+1}}$ ${\displaystyle g_{i}}$ ${\displaystyle h_{i}}$ ${\displaystyle G}$ ${\displaystyle H}$ ${\displaystyle G}$ ${\displaystyle H}$

Grupo de simetría

La aplicación de la construcción de ida y vuelta a dos subgrafos finitos isomorfos cualesquiera del grafo de Rado extiende su isomorfismo a un automorfismo de todo el grafo de Rado. El hecho de que todo isomorfismo de subgrafos finitos se extienda a un automorfismo de todo el grafo se expresa diciendo que el grafo de Rado es ultrahomogéneo . En particular, hay un automorfismo que lleva cualquier par ordenado de vértices adyacentes a cualquier otro par ordenado de ese tipo, por lo que el grafo de Rado es un grafo simétrico . ^[12]

El grupo de automorfismos del grafo de Rado es un grupo simple , cuyo número de elementos es la cardinalidad del continuo . Cada subgrupo de este grupo cuyo índice es menor que la cardinalidad del continuo contiene el estabilizador puntual de un conjunto finito de vértices, y además está contenido dentro del estabilizador por conjuntos del mismo conjunto. ^[14] La afirmación sobre los estabilizadores puntuales se denomina propiedad de índice pequeño, ^[14] y demostrarla requería mostrar que para cada grafo finito , hay un grafo finito que contiene como un subgrafo inducido tal que cada isomorfismo entre subgrafos inducidos de se extiende a un automorfismo de . ^[15] Esto se denomina propiedad de extensión para automorfismos parciales y desde entonces se ha generalizado a otras estructuras para mostrar la propiedad de índice pequeño y otras propiedades. ^[16] ${\displaystyle X}$ ${\displaystyle Z}$ ${\displaystyle X}$ ${\displaystyle X}$ ${\displaystyle Z}$

La construcción del grafo de Rado como un grafo circulante infinito muestra que su grupo de simetría incluye automorfismos que generan un grupo cíclico infinito transitivo . El conjunto de diferencias de esta construcción (el conjunto de distancias en los enteros entre vértices adyacentes) puede restringirse para incluir la diferencia 1, sin afectar la corrección de esta construcción, de lo que se sigue que el grafo de Rado contiene un camino hamiltoniano infinito cuyas simetrías son un subgrupo de las simetrías de todo el grafo. ^[17]

Robustez frente a cambios finitos

Si se forma un gráfico a partir del gráfico de Rado eliminando cualquier número finito de aristas o vértices, o añadiendo un número finito de aristas, el cambio no afecta a la propiedad de extensión del gráfico. Para cualquier par de conjuntos y todavía es posible encontrar un vértice en el gráfico modificado que sea adyacente a todo en y no adyacente a todo en , añadiendo las partes modificadas de a y aplicando la propiedad de extensión en el gráfico de Rado sin modificar. Por lo tanto, cualquier modificación finita de este tipo da como resultado un gráfico que es isomorfo al gráfico de Rado. ^[18] ${\displaystyle G}$ ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle G}$ ${\displaystyle V}$

Particiones

Para cualquier partición de los vértices del grafo de Rado en dos conjuntos y , o más generalmente para cualquier partición en un número finito de subconjuntos, al menos uno de los subgrafos inducidos por uno de los conjuntos de partición es isomorfo a todo el grafo de Rado. Cameron (2001) da la siguiente prueba corta: si ninguna de las partes induce un subgrafo isomorfo al grafo de Rado, todas ellas no tienen la propiedad de extensión, y se pueden encontrar pares de conjuntos y que no se pueden extender dentro de cada subgrafo. Pero entonces, la unión de los conjuntos y la unión de los conjuntos formarían un conjunto que no se podría extender en todo el grafo, contradiciendo la propiedad de extensión del grafo de Rado. Esta propiedad de ser isomorfo a uno de los subgrafos inducidos de cualquier partición la mantienen solo tres grafos no dirigidos infinitos numerables: el grafo de Rado, el grafo completo y el grafo vacío . ^[19] Bonato, Cameron y Delić (2000) y Diestel et al. (2007) investigan gráficos dirigidos infinitos con la misma propiedad de partición; todos se forman eligiendo orientaciones para los bordes del gráfico completo o el gráfico de Rado. ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle U_{i}}$ ${\displaystyle V_{i}}$ ${\displaystyle U_{i}}$ ${\displaystyle V_{i}}$

Un resultado relacionado con esto se refiere a particiones de aristas en lugar de particiones de vértices: para cada partición de las aristas del grafo de Rado en un número finito de conjuntos, hay un subgrafo isomorfo a todo el grafo de Rado que utiliza como máximo dos de los colores. Sin embargo, no necesariamente puede existir un subgrafo isomorfo que utilice solo un color de aristas. ^[20] De manera más general, para cada grafo finito hay un número (llamado el gran grado de Ramsey de en el grafo de Rado) tal que para cada partición de las copias de en el grafo de Rado en un número finito de conjuntos, hay un subgrafo inducido isomorfo a todo el grafo de Rado que utiliza como máximo los colores. ^{[21] [22]} ${\displaystyle A}$ ${\displaystyle d_{A}}$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle d_{A}}$

Teoría de modelos y leyes 0-1

Fagin (1976) utilizó el gráfico de Rado para demostrar una ley cero-uno para enunciados de primer orden en la lógica de grafos . Cuando un enunciado lógico de este tipo es verdadero o falso para el gráfico de Rado, también es verdadero o falso (respectivamente) para casi todos los grafos finitos.

Propiedades de primer orden

El lenguaje de primer orden de los grafos es la colección de oraciones bien formadas en lógica matemática formadas a partir de variables que representan los vértices de los grafos, cuantificadores universales y existenciales , conectivos lógicos y predicados para la igualdad y adyacencia de los vértices. Por ejemplo, la condición de que un grafo no tenga ningún vértice aislado puede expresarse mediante la oración donde el símbolo indica la relación de adyacencia entre dos vértices. ^[23] Esta oración es verdadera para algunos grafos y falsa para otros; se dice que un grafo modela , escrito , si es verdadero para los vértices y la relación de adyacencia de . ^[24] $${\displaystyle \forall u:\exists v:u\sim v}$$ ${\displaystyle \sim }$ ${\displaystyle S}$ ${\displaystyle G}$ ${\displaystyle S}$ ${\displaystyle G\models S}$ ${\displaystyle S}$ ${\displaystyle G}$

La propiedad de extensión del gráfico de Rado puede expresarse mediante una colección de oraciones de primer orden , que establecen que para cada elección de vértices en un conjunto y vértices en un conjunto , todos distintos, existe un vértice adyacente a todo en y no adyacente a todo en . ^[25] Por ejemplo, puede escribirse como ${\displaystyle E_{i,j}}$ ${\displaystyle i}$ ${\displaystyle A}$ ${\displaystyle j}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle E_{1,1}}$ $${\displaystyle \forall a:\forall b:a\neq b\rightarrow \exists c:c\neq a\wedge c\neq b\wedge c\sim a\wedge \lnot (c\sim b).}$$

Lo completo

Gaifman (1964) demostró que las oraciones , junto con oraciones adicionales que establecen que la relación de adyacencia es simétrica y antirreflexiva (es decir, que un grafo que modela estas oraciones no está dirigido y no tiene bucles propios), son los axiomas de una teoría completa . Esto significa que, para cada oración de primer orden , exactamente uno de y su negación se puede demostrar a partir de estos axiomas. Debido a que el grafo de Rado modela los axiomas de extensión, modela todas las oraciones en esta teoría. ^[26] ${\displaystyle E_{i,j}}$ ${\displaystyle S}$ ${\displaystyle S}$

En lógica, una teoría que tiene un solo modelo (salvo isomorfismo) con una cardinalidad infinita dada se llama -categórica . El hecho de que el grafo de Rado sea el único grafo numerable con la propiedad de extensión implica que también es el único modelo numerable para su teoría. Esta propiedad de unicidad del grafo de Rado se puede expresar diciendo que la teoría del grafo de Rado es ω-categórica . Łoś y Vaught demostraron en 1954 que cuando una teoría es –categórica (para algún cardinal infinito ) y, además, no tiene modelos finitos, entonces la teoría debe ser completa. ^[27] Por lo tanto, el teorema de Gaifman de que la teoría del grafo de Rado es completa se deduce de la unicidad del grafo de Rado por la prueba de Łoś–Vaught . ^[28] ${\displaystyle \lambda }$ ${\displaystyle \lambda }$ ${\displaystyle \lambda }$ ${\displaystyle \lambda }$

Grafos finitos y complejidad computacional

Como Fagin (1976) demostró, las oraciones de primer orden demostrables a partir de los axiomas de extensión y modeladas por el grafo de Rado son exactamente las oraciones verdaderas para casi todos los grafos finitos aleatorios. Esto significa que si uno elige un grafo de vértice uniformemente al azar entre todos los grafos en vértices etiquetados, entonces la probabilidad de que tal oración sea verdadera para el grafo elegido se acerca a uno en el límite cuando tiende a infinito. Simétricamente, las oraciones que no están modeladas por el grafo de Rado son falsas para casi todos los grafos finitos aleatorios. De ello se deduce que cada oración de primer orden es casi siempre verdadera o casi siempre falsa para grafos finitos aleatorios, y estas dos posibilidades se pueden distinguir determinando si el grafo de Rado modela la oración. La prueba de Fagin utiliza el teorema de compacidad . ^[29] Con base en esta equivalencia, la teoría de oraciones modeladas por el grafo de Rado se ha llamado "la teoría del grafo aleatorio" o "la teoría casi segura de grafos". ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle n}$

Debido a esta ley 0-1, es posible probar si cualquier oración particular de primer orden es modelada por el grafo de Rado en una cantidad finita de tiempo, eligiendo un valor suficientemente grande de y contando el número de grafos de -vértice que modelan la oración. Sin embargo, aquí, "suficientemente grande" es al menos exponencial en el tamaño de la oración. Por ejemplo, el axioma de extensión implica la existencia de una camarilla de -vértice , pero una camarilla de ese tamaño existe con alta probabilidad solo en grafos aleatorios de tamaño exponencial en . Es poco probable que determinar si el grafo de Rado modela una oración dada se pueda hacer más rápidamente que en tiempo exponencial, ya que el problema es PSPACE-completo . ^[30] ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle E_{k,0}}$ ${\displaystyle (k+1)}$ ${\displaystyle k}$

Otras propiedades de la teoría de modelos

El gráfico de Rado es ultrahomogéneo y, por lo tanto, es el límite de Fraïssé de su clase de subestructuras finitas, es decir, la clase de gráficos finitos. ^[31] Dado que también está en un lenguaje relacional finito, la ultrahomogeneidad es equivalente a que su teoría tenga eliminación de cuantificadores y sea ω-categórica. ^[32] Como el gráfico de Rado es, por lo tanto, el modelo contable de una teoría ω-categórica contable, es a la vez primo y saturado . ^{[33] [34]}

La teoría del grafo de Rado es un ejemplo prototípico de una teoría con la propiedad de independencia y de una teoría simple que no es estable . ^[35]

Conceptos relacionados

Aunque el gráfico de Rado es universal para subgrafos inducidos, no lo es para incrustaciones isométricas de grafos, donde una incrustación isométrica es un isomorfismo de grafo que conserva la distancia . El gráfico de Rado tiene un diámetro de dos, por lo que cualquier grafo con un diámetro mayor no se incrusta isométricamente en él. Moss (1989, 1991) ha descrito una familia de grafos universales para incrustaciones isométricas, uno para cada diámetro de grafo finito posible; el grafo de su familia con diámetro dos es el gráfico de Rado.

Los grafos de Henson son grafos contables (uno por cada entero positivo ) que no contienen una camarilla de vértices y son universales para grafos sin camarillas. Pueden construirse como subgrafos inducidos del grafo de Rado. ^[17] El grafo de Rado, los grafos de Henson y sus complementos, las uniones disjuntas de camarillas infinitas contables y sus complementos, y las uniones disjuntas infinitas de camarillas finitas isomorfas y sus complementos son los únicos grafos homogéneos infinitos contables posibles . ^[36] ${\displaystyle i}$ ${\displaystyle i}$ ${\displaystyle i}$

La propiedad de universalidad del grafo de Rado se puede extender a grafos con aristas coloreadas; es decir, grafos en los que las aristas han sido asignadas a diferentes clases de color, pero sin el requisito habitual de coloración de aristas de que cada clase de color forme un . Para cualquier número finito o infinito numerable de colores , existe un grafo único con aristas coloreadas infinito numerable de modo que cada isomorfismo parcial de un grafo finito con aristas coloreadas se puede extender a un isomorfismo completo. Con esta notación, el grafo de Rado es simplemente . Truss (1985) investiga los grupos de automorfismos de esta familia más general de grafos. ${\displaystyle \chi }$ ${\displaystyle \chi }$ ${\displaystyle G_{\chi }}$ ${\displaystyle \chi }$ ${\displaystyle G_{1}}$

Si bien el gráfico de Rado es universal contable para la clase de todos los gráficos, no todas las clases de gráficos tienen un gráfico universal contable. Por ejemplo, no existe ningún gráfico contable que omita el ciclo de 4 como subgráfico que contenga todos los demás gráficos contables como subgráficos (no necesariamente inducidos). ^[37]

De las consideraciones de la teoría de modelos clásicos para construir un modelo saturado se desprende que, bajo la hipótesis del continuo CH, existe un grafo universal con un número continuo de vértices. Por supuesto, bajo CH, el continuo es igual a , el primer cardinal incontable . Shelah (1984, 1990) utiliza el forzamiento para investigar grafos universales con muchos vértices y demuestra que, incluso en ausencia de CH, puede existir un grafo universal de tamaño . También investiga cuestiones análogas para cardinalidades superiores. ${\displaystyle \aleph _{1}}$ ${\displaystyle \aleph _{1}}$ ${\displaystyle \aleph _{1}}$

Notas

1. Ackermann (1937); Rado (1964).
2. Véase Cameron (1997), Hecho 1 y su prueba.
3. Erdős y Rényi (1963).
4. Cameron (1997), Proposición 5.
5. Cameron (1997), Teorema 2.
6. Cameron (1997, 2001)
7. Cameron (1997), Sección 1.2.
8. Horsley, Pike y Sanaei (2011)
9. Hodges (1997), pág. 350.
10. Esencialmente, la misma construcción, descrita en términos de teoría de conjuntos en lugar de utilizar números binarios, se da como Teorema 2 de Cameron (1997).
11. Cameron (1997), Proposición 6.
12. Cameron (2001).
13. Cameron (1997), Hecho 2.
14. Cameron (1997), Sección 1.8: El grupo de automorfismos.
15. Grushovski (1992)
16. Macpherson (2011), Secciones 5.2 y 5.3.
17. Henson (1971).
18. Cameron (1997), Sección 1.3: Indestructibilidad.
19. Cameron (1990); Diestel et al. (2007).
20. Pouzet y Sauer (1996).
21. Sauer (2006)
22. Döbrinen (2021)
23. Spencer (2001), Sección 1.2, "¿Qué es una teoría de primer orden?", págs. 15-17.
24. Véase, por ejemplo, Grandjean (1983), pág. 184.
25. Spencer (2001), Sección 1.3, "Declaraciones de extensión y gráficos con raíz", págs. 17-18.
26. Gaifman (1964); Marker (2002), Teorema 2.4.2, pág. 50.
27. Loś (1954); Vaught (1954); Enderton (1972), pág. 147.
28. Marker (2002), Teorema 2.2.6, pág. 42.
29. Fagin (1976); Marker (2002), Teorema 2.4.4, págs. 51–52.
30. Grandjean (1983).
31. Macpherson (2011), Teorema 2.1.3, Ejemplo 2.2.1.
32. Macpherson (2011), Corolario 3.1.3, Proposición 3.1.6.
33. Rothmaler (2000), Teorema 13.3.1, Teorema 13.2.1.
34. McNulty (2016), pág. 71 y pág. 75.
35. Baldwin (2018)
36. Lachlan y Woodrow (1980).
37. Cherlin (2011), Hecho 1.3

Referencias

• Ackermann, Wilhelm (1937), "Die Widerspruchsfreiheit der allgemeinen Mengenlehre", Mathematische Annalen , 114 (1): 305–315, doi :10.1007/BF01594179, S2CID  120576556
• Bonato, Anthony; Cameron, Peter ; Delić, Dejan (2000), "Torneos y órdenes con la propiedad pigeonhole", Canadian Mathematical Bulletin , 43 (4): 397–405, doi : 10.4153/CMB-2000-047-6 , MR  1793941.
• Baldwin, John T. (2018), Teoría de modelos y filosofía de la práctica matemática: formalización sin fundacionalismo , Cambridge University Press, doi :10.1017/9781316987216, ISBN 978-1-107-18921-8, MR  3793636, S2CID  126311148.
• Cameron, Peter J. (1990), Grupos de permutación oligomórfica , London Mathematical Society Lecture Note Series, vol. 152, Cambridge: Cambridge University Press, ISBN 0-521-38836-8, Sr.  1066691.
• Cameron, Peter J. (1997), "El grafo aleatorio", Las matemáticas de Paul Erdős, II , Algorithms and Combinatorics , vol. 14, Berlín: Springer, págs. 333–351, arXiv : 1301.7544 , Bibcode :2013arXiv1301.7544C, MR  1425227.
• Cameron, Peter J. (2001), "El gráfico aleatorio revisitado" (PDF) , Congreso Europeo de Matemáticas , vol. I (Barcelona, ​​2000) , Progr. Math., vol. 201, Basilea: Birkhäuser, págs. 267–274, doi :10.1007/978-3-0348-8268-2_15, MR  1905324.
• Cherlin, Gregory (2011), "Subestructuras prohibidas y dicotomías combinatorias: WQO y universalidad", Discrete Mathematics , 311 (15): 1543–1584, doi :10.1016/j.disc.2011.03.014, MR  2800977.
• Diestel, Reinhard; Leader, Imre ; Scott, Alex; Thomassé, Stéphan (2007), "Particiones y orientaciones del gráfico de Rado", Transactions of the American Mathematical Society , 359 (5): 2395–2405, doi : 10.1090/S0002-9947-06-04086-4 , MR  2276626.
• Dobrinen, Natasha (2021), "Teoría de estructuras homogéneas de Ramsey: tendencias actuales y problemas abiertos", arXiv : 2110.00655v1 [math.LO].
• Enderton, Herbert B. (1972), Una introducción matemática a la lógica , Academic Press, Nueva York-Londres, MR  0337470.
• Erdős, P .; Rényi, A. (1963), "Gráficos asimétricos", Acta Mathematica Academiae Scientiarum Hungaricae , 14 (3–4): 295–315, doi : 10.1007/BF01895716 , SEÑOR  0156334.
• Fagin, Ronald (1976), "Probabilidades en modelos finitos" (PDF) , The Journal of Symbolic Logic , 41 (1): 50–58, doi :10.1017/s0022481200051756, JSTOR  2272945, MR  0476480, S2CID  2563318, archivado desde el original (PDF) el 2016-03-04 , consultado el 2014-09-05.
• Gaifman, Haim (1964), "Sobre las medidas en los cálculos de primer orden", Israel Journal of Mathematics , 2 : 1–18, doi : 10.1007/BF02759729 , MR  0175755.
• Grandjean, Étienne (1983), "Complejidad de la teoría de primer orden de casi todas las estructuras finitas", Información y Control , 57 (2–3): 180–204, doi : 10.1016/S0019-9958(83)80043-6 , MR  0742707.
• Henson, C. Ward (1971), "Una familia de grafos homogéneos contables", Pacific Journal of Mathematics , 38 : 69–83, doi : 10.2140/pjm.1971.38.69 , MR  0304242.
• Hodges, Wilfrid (1997), Una teoría de modelos más breve , Cambridge University Press, ISBN 0-521-58713-1, OCLC  468298248
• Horsley, Daniel; Pike, David A.; Sanaei, Asiyeh (2011), "Cierre existencial de gráficos de intersección de bloques de diseños infinitos que tienen un tamaño de bloque infinito", Journal of Combinatorial Designs , 19 (4): 317–327, doi :10.1002/jcd.20283, MR  2838911, S2CID  120707836.
• Hrushovski, Ehud (1992), "Extensión de isomorfismos parciales de grafos", Combinatorica , 12 (4): 411–416, doi :10.1007/BF01305233, MR  1194731, S2CID  19939702.
• Lachlan, AH; Woodrow, Robert E. (1980), "Grafos no dirigidos ultrahomogéneos contables", Transactions of the American Mathematical Society , 262 (1): 51–94, doi : 10.2307/1999974 , JSTOR  1999974, MR  0583847.
• Łoś, J. (1954), "Sobre la categoricidad en el poder de los sistemas deductivos elementales y algunos problemas relacionados", Colloquium Math. , 3 : 58–62, doi : 10.4064/cm-3-1-58-62 , MR  0061561.
• Macpherson, Dugald (2011), "Un estudio de estructuras homogéneas", Discrete Mathematics , 311 (15): 1599–1634, doi : 10.1016/j.disc.2011.01.024 , MR  2800979.
• Marker, David (2002), Teoría de modelos , Textos de posgrado en matemáticas, vol. 217, Springer-Verlag, Nueva York, ISBN 0-387-98760-6, Sr.  1924282.
• McNulty, George F. (2016), Teoría de modelos elementales (PDF) , págs. 71–75 , consultado el 5 de abril de 2023.
• Moss, Lawrence S. (1989), "Existencia e inexistencia de gráficos universales", Polska Akademia Nauk. Fundamenta Mathematicae , 133 (1): 25–37, doi : 10.4064/fm-133-1-25-37 , SEÑOR  1059159.
• Moss, Lawrence S. (1991), "Los grafos universales de diámetro finito fijo", Teoría de grafos, combinatoria y aplicaciones. Vol. 2 (Kalamazoo, MI, 1988) , Wiley-Intersci. Publ., Nueva York: Wiley, págs. 923–937, MR  1170834.
• Pouzet, Maurice; Sauer, Norbert (1996), "Particiones de borde del gráfico de Rado", Combinatorica , 16 (4): 505–520, doi :10.1007/BF01271269, MR  1433638, S2CID  206793062.
• Rado, Richard (1964), "Gráficos universales y funciones universales" (PDF) , Acta Arith. , 9 (4): 331–340, doi :10.4064/aa-9-4-331-340.
• Rothmaler, Philipp (2000), Introducción a la teoría de modelos , Álgebra, lógica y aplicaciones, vol. 15, Gordon and Breach Science Publishers, ISBN 90-5699-287-2, Sr.  1800596.
• Sauer, Norbert (2006), "Coloración de subgrafos del gráfico de Rado", Combinatorica , 26 (2): 231–253, doi :10.1007/s00493-006-0015-0, MR  2223636, S2CID  19251747.
• Shelah, Saharon (1984), "Sobre grafos universales sin instancias de CH", Anales de lógica pura y aplicada , 26 (1): 75–87, doi : 10.1016/0168-0072(84)90042-3 , MR  0739914.
• Shelah, Saharon (1990), "Gráficos universales sin instancias de CH: revisitados", Israel Journal of Mathematics , 70 (1): 69–81, doi : 10.1007/BF02807219 , MR  1057268.
• Spencer, Joel (2001), La extraña lógica de los grafos aleatorios , Algorithms and Combinatorics, vol. 22, Springer-Verlag, Berlín, doi :10.1007/978-3-662-04538-1, ISBN 3-540-41654-4, MR  1847951, S2CID  118026950.
• Truss, JK (1985), "El grupo del grafo universal contable", Mathematical Proceedings of the Cambridge Philosophical Society , 98 (2): 213–245, Bibcode :1985MPCPS..98..213T, doi :10.1017/S0305004100063428, MR  0795890, S2CID  122772888.
• Vaught, Robert L. (1954), "Aplicaciones del teorema de Löwenheim-Skolem-Tarski a problemas de completitud y decidibilidad", Indagationes Mathematicae , 16 : 467–472, doi :10.1016/S1385-7258(54)50058-2, MR  0063993.