
Los diagramas matemáticos , como cuadros y gráficos , están diseñados principalmente para transmitir relaciones matemáticas, por ejemplo, comparaciones a lo largo del tiempo. [1]

Un número complejo se puede representar visualmente como un par de números que forman un vector en un diagrama llamado diagrama de Argand. El plano complejo a veces se llama plano de Argand porque se usa en los diagramas de Argand . Estos reciben su nombre de Jean-Robert Argand (1768-1822), aunque fueron descritos por primera vez por el agrimensor y matemático noruego-danés Caspar Wessel (1745-1818). [2] Los diagramas de Argand se usan con frecuencia para trazar las posiciones de los polos y ceros de una función en el plano complejo.
El concepto de plano complejo permite una interpretación geométrica de los números complejos. En la suma , se suman como vectores . La multiplicación de dos números complejos se puede expresar más fácilmente en coordenadas polares : la magnitud o módulo del producto es el producto de los dos valores absolutos , o módulos, y el ángulo o argumento del producto es la suma de los dos ángulos, o argumentos. En particular, la multiplicación por un número complejo de módulo 1 actúa como una rotación.
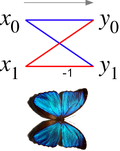
En el contexto de los algoritmos de transformada rápida de Fourier , una mariposa es una parte del cálculo que combina los resultados de transformadas de Fourier discretas (DFT) más pequeñas en una DFT más grande, o viceversa (dividiendo una DFT más grande en subtransformaciones). El nombre "mariposa" proviene de la forma del diagrama de flujo de datos en el caso de base 2, como se describe a continuación. La misma estructura también se puede encontrar en el algoritmo de Viterbi , utilizado para encontrar la secuencia más probable de estados ocultos.
El diagrama de mariposa muestra un diagrama de flujo de datos que conecta las entradas x (izquierda) con las salidas y que dependen de ellas (derecha) para un paso de "mariposa" de un algoritmo de FFT de Cooley-Tukey de base 2. Este diagrama se parece a una mariposa, como en la mariposa Morpho que se muestra a modo de comparación, de ahí el nombre.

En matemáticas, y especialmente en teoría de categorías , un diagrama conmutativo es un diagrama de objetos , también conocidos como vértices, y morfismos , también conocidos como flechas o aristas, tales que al seleccionar dos objetos cualquier camino dirigido a través del diagrama conduce al mismo resultado por composición.
Los diagramas conmutativos desempeñan en la teoría de categorías el mismo papel que las ecuaciones en el álgebra.

Un diagrama de Hasse es una representación sencilla de un conjunto finito parcialmente ordenado , que forma un dibujo de la reducción transitiva del orden parcial . Concretamente, se representa cada elemento del conjunto como un vértice en la página y se dibuja un segmento de línea o curva que va hacia arriba desde x hasta y precisamente cuando x < y y no hay z tal que x < z < y . En este caso, decimos que y cubre a x, o y es un sucesor inmediato de x. En un diagrama de Hasse, se requiere que las curvas se dibujen de manera que cada una se encuentre exactamente con dos vértices: sus dos puntos finales. Cualquier diagrama de este tipo (suponiendo que los vértices estén etiquetados) determina de forma única un orden parcial, y cualquier orden parcial tiene una reducción transitiva única, pero hay muchas posibles ubicaciones de elementos en el plano, lo que da como resultado diferentes diagramas de Hasse para un orden dado que pueden tener apariencias muy variadas.

En la teoría de nudos, una forma útil de visualizar y manipular nudos es proyectarlos sobre un plano (pensemos en el nudo que proyecta una sombra sobre la pared). Una pequeña perturbación en la elección de la proyección garantizará que sea biunívoca, excepto en los puntos dobles, llamados cruces , donde la "sombra" del nudo se cruza a sí misma una vez transversalmente [3].
En cada cruce hay que indicar qué sección está "por encima" y cuál "por debajo", para poder recrear el nudo original. Esto se hace a menudo creando una ruptura en la hebra que pasa por debajo. Si siguiendo el diagrama el nudo se cruza alternativamente "por encima" y "por debajo", entonces el diagrama representa una clase de nudo particularmente bien estudiada, los nudos alternados .

Un diagrama de Venn es una representación de conjuntos matemáticos: un diagrama matemático que representa conjuntos como círculos, con sus relaciones entre sí expresadas a través de sus posiciones superpuestas, de modo que se muestran todas las relaciones posibles entre los conjuntos. [4]
El diagrama de Venn se construye con una colección de curvas cerradas simples dibujadas en el plano. El principio de estos diagramas es que las clases se representan por regiones en tal relación entre sí que todas las posibles relaciones lógicas de estas clases se pueden indicar en el mismo diagrama. Es decir, el diagrama inicialmente deja espacio para cualquier posible relación de las clases, y la relación real o dada, luego se puede especificar indicando que alguna región particular es nula o no es nula. [5]

Un diagrama de Voronoi es un tipo especial de descomposición de un espacio métrico determinado por las distancias a un conjunto discreto específico de objetos en el espacio, por ejemplo, por un conjunto discreto de puntos. Este diagrama recibe su nombre en honor a Georgy Voronoi , y también se denomina teselación de Voronoi , descomposición de Voronoi o teselación de Dirichlet en honor a Peter Gustav Lejeune Dirichlet .
En el caso más simple, se nos da un conjunto de puntos S en el plano, que son los sitios de Voronoi. Cada sitio s tiene una celda de Voronoi V(s) que consiste en todos los puntos más cercanos a s que a cualquier otro sitio. Los segmentos del diagrama de Voronoi son todos los puntos en el plano que son equidistantes a dos sitios. Los nodos de Voronoi son los puntos equidistantes a tres (o más) sitios.

Un grupo de papel tapiz , grupo de simetría plana o grupo cristalográfico plano es una clasificación matemática de un patrón repetitivo bidimensional, basada en las simetrías del patrón. Dichos patrones se dan con frecuencia en la arquitectura y el arte decorativo. Hay 17 grupos distintos posibles .
Los grupos de papel tapiz son grupos de simetría bidimensionales , de complejidad intermedia entre los grupos de frisos más simples y los grupos cristalográficos tridimensionales , también llamados grupos espaciales . Los grupos de papel tapiz clasifican los patrones por sus simetrías. Las diferencias sutiles pueden ubicar patrones similares en grupos diferentes, mientras que los patrones que son muy diferentes en estilo, color, escala u orientación pueden pertenecer al mismo grupo.
Un diagrama de Young o cuadro de Young , también llamado diagrama de Ferrers , es una colección finita de cajas o celdas, dispuestas en filas justificadas a la izquierda, con tamaños de fila que disminuyen débilmente (cada fila tiene la misma longitud o una longitud más corta que su predecesora).

Al enumerar el número de casillas en cada fila se obtiene una partición de un entero positivo n , el número total de casillas del diagrama. Se dice que el diagrama de Young tiene forma , y contiene la misma información que esa partición. Al enumerar el número de casillas en cada columna se obtiene otra partición, la partición conjugada o transpuesta de ; se obtiene un diagrama de Young de esa forma reflejando el diagrama original a lo largo de su diagonal principal.
Los cuadros de Young fueron introducidos por Alfred Young , un matemático de la Universidad de Cambridge , en 1900. Luego fueron aplicados al estudio del grupo simétrico por Georg Frobenius en 1903. Su teoría fue desarrollada posteriormente por muchos matemáticos.