esfera de riemann

Modelo del plano complejo extendido más un punto en el infinito

La esfera de Riemann se puede visualizar como el plano numérico complejo enrollado alrededor de una esfera (mediante alguna forma de proyección estereográfica ; los detalles se dan a continuación).

En matemáticas , la esfera de Riemann , llamada así en honor a Bernhard Riemann , ^[1] es un modelo del plano complejo extendido (también llamado plano complejo cerrado ): el plano complejo más un punto en el infinito . Este plano extendido representa los números complejos extendidos , es decir, los números complejos más un valor para el infinito . En el modelo de Riemann, el punto se aproxima a números muy grandes, del mismo modo que el punto se aproxima a números muy pequeños. ${\displaystyle \infty }$ ${\displaystyle \infty }$ ${\displaystyle 0}$

Los números complejos extendidos son útiles en el análisis complejo porque permiten la división por cero en algunas circunstancias, de una manera que hace que expresiones como se porten bien . Por ejemplo, cualquier función racional en el plano complejo se puede extender a una función holomorfa en la esfera de Riemann, con los polos de la función racional mapeándose hasta el infinito. De manera más general, cualquier función meromorfa puede considerarse como una función holomorfa cuyo codominio es la esfera de Riemann. ${\displaystyle 1/0=\infty }$

En geometría , la esfera de Riemann es el ejemplo prototípico de una superficie de Riemann y es una de las variedades complejas más simples . En geometría proyectiva , la esfera es un ejemplo de un espacio proyectivo complejo y puede considerarse como la línea proyectiva compleja , el espacio proyectivo de todas las líneas complejas . Como ocurre con cualquier superficie compacta de Riemann, la esfera también puede verse como una curva algebraica proyectiva , lo que la convierte en un ejemplo fundamental en geometría algebraica . También encuentra utilidad en otras disciplinas que dependen del análisis y la geometría, como la esfera de Bloch de la mecánica cuántica y en otras ramas de la física . ${\displaystyle \mathbf {P} ^{1}(\mathbf {C} )}$ ${\displaystyle \mathbf {C} ^{2}}$

Números complejos extendidos

Los números complejos extendidos constan de números complejos junto con . El conjunto de números complejos extendidos puede escribirse como y, a menudo, se denota añadiendo alguna decoración a la letra , como ${\displaystyle \mathbf {C} }$ ${\displaystyle \infty }$ ${\displaystyle \mathbf {C} \cup \{\infty \}}$ ${\displaystyle \mathbf {C} }$

${\displaystyle {\widehat {\mathbf {C} }},\quad {\overline {\mathbf {C} }},\quad {\text{or}}\quad \mathbf {C} _{\infty }.}$

La notación también se ha utilizado, pero como esta notación también se usa para el plano perforado , puede generar ambigüedad. ^[2] ${\displaystyle \mathbf {C} ^{*}}$ ${\displaystyle \mathbf {C} \setminus \{0\}}$

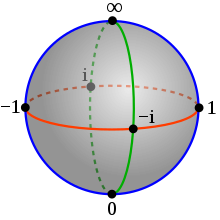
Geométricamente, el conjunto de números complejos extendidos se denomina esfera de Riemann (o plano complejo extendido ).

Operaciones aritmeticas

La suma de números complejos se puede ampliar definiendo, para , ${\displaystyle z\in \mathbf {C} }$

${\displaystyle z+\infty =\infty }$

para cualquier número complejo , y la multiplicación puede definirse por ${\displaystyle z}$

${\displaystyle z\times \infty =\infty }$

para todos los números complejos distintos de cero , con . Tenga en cuenta que y quedan sin definir . A diferencia de los números complejos, los números complejos extendidos no forman un cuerpo , ya que no tienen inverso aditivo ni multiplicativo . Sin embargo, se acostumbra definir la división por ${\displaystyle z}$ ${\displaystyle \infty \times \infty =\infty }$ ${\displaystyle \infty -\infty }$ ${\displaystyle 0\times \infty }$ ${\displaystyle \infty }$ ${\displaystyle \mathbf {C} \cup \{\infty \}}$

${\displaystyle {\frac {z}{0}}=\infty \quad {\text{and}}\quad {\frac {z}{\infty }}=0}$

para todos los números complejos distintos de cero con y . Los cocientes y quedan sin definir. ${\displaystyle z}$ ${\displaystyle \infty /0=\infty }$ ${\displaystyle 0/\infty =0}$ ${\displaystyle 0/0}$ ${\displaystyle \infty /\infty }$

Funciones racionales

Cualquier función racional (en otras palabras, es la razón de funciones polinómicas y con coeficientes complejos, tales que y no tienen factor común) se puede extender a una función continua en la esfera de Riemann. Específicamente, si es un número complejo tal que el denominador es cero pero el numerador es distinto de cero, entonces se puede definir como . Además, puede definirse como el límite de as , que puede ser finito o infinito. ${\displaystyle f(z)=g(z)/h(z)}$ ${\displaystyle f(z)}$ ${\displaystyle g(z)}$ ${\displaystyle h(z)}$ ${\displaystyle z}$ ${\displaystyle g(z)}$ ${\displaystyle h(z)}$ ${\displaystyle z_{0}}$ ${\displaystyle h(z_{0})}$ ${\displaystyle g(z_{0})}$ ${\displaystyle f(z_{0})}$ ${\displaystyle \infty }$ ${\displaystyle f(\infty )}$ ${\displaystyle f(z)}$ ${\displaystyle z\to \infty }$

El conjunto de funciones racionales complejas, cuyo símbolo matemático es, forman todas las funciones holomorfas posibles desde la esfera de Riemann hacia sí misma, cuando se la ve como una superficie de Riemann , excepto la función constante que toma el valor en todas partes. Las funciones de forman un campo algebraico, conocido como campo de funciones racionales en la esfera . ${\displaystyle \mathbf {C} (z)}$ ${\displaystyle \infty }$ ${\displaystyle \mathbf {C} (z)}$

Por ejemplo, dada la función

${\displaystyle f(z)={\frac {6z^{2}+1}{2z^{2}-50}}}$

podemos definir , ya que el denominador es cero en y desde como . Usando estas definiciones, se convierte en una función continua desde la esfera de Riemann hacia sí misma. ${\displaystyle f(\pm 5)=\infty }$ ${\displaystyle \pm 5}$ ${\displaystyle f(\infty )=3}$ ${\displaystyle f(z)\to 3}$ ${\displaystyle z\to \infty }$ ${\displaystyle f}$

Como una variedad compleja

Como variedad compleja unidimensional , la esfera de Riemann se puede describir mediante dos gráficos , ambos con dominio igual al plano de números complejos . Sea un número complejo en una copia de y sea un número complejo en otra copia de . Identifique cada número complejo distinto de cero del primero con el número complejo distinto de cero del segundo . Entonces el mapa ${\displaystyle \mathbf {C} }$ ${\displaystyle \zeta }$ ${\displaystyle \mathbf {C} }$ ${\displaystyle \xi }$ ${\displaystyle \mathbf {C} }$ ${\displaystyle \zeta }$ ${\displaystyle \mathbf {C} }$ ${\displaystyle 1/\xi }$ ${\displaystyle \mathbf {C} }$

${\displaystyle f(z)={\frac {1}{z}}}$

Se llama mapa de transición entre las dos copias de los llamados gráficos, pegándolas entre sí. Dado que los mapas de transición son holomorfos , definen una variedad compleja, llamada esfera de Riemann . Como variedad compleja de 1 dimensión compleja (es decir, 2 dimensiones reales), también se denomina superficie de Riemann . ${\displaystyle \mathbf {C} }$

Intuitivamente, los mapas de transición indican cómo unir dos planos para formar la esfera de Riemann. Los planos están pegados "de adentro hacia afuera", de modo que se superponen casi en todas partes, y cada plano contribuye solo con un punto (su origen) que falta en el otro plano. En otras palabras, (casi) cada punto de la esfera de Riemann tiene tanto un valor como un valor, y los dos valores están relacionados por . El punto donde debería tener -valor " "; en este sentido, el origen del gráfico juega el papel de en el gráfico. Simétricamente, el origen del gráfico juega el papel de en el gráfico. ${\displaystyle \zeta }$ ${\displaystyle \xi }$ ${\displaystyle \zeta =1/\xi }$ ${\displaystyle \xi =0}$ ${\displaystyle \zeta }$ ${\displaystyle 1/0}$ ${\displaystyle \xi }$ ${\displaystyle \infty }$ ${\displaystyle \zeta }$ ${\displaystyle \zeta }$ ${\displaystyle \infty }$ ${\displaystyle \xi }$

Topológicamente , el espacio resultante es la compactación en un punto de un plano en la esfera. Sin embargo, la esfera de Riemann no es simplemente una esfera topológica. Es una esfera con una estructura compleja bien definida , de modo que alrededor de cada punto de la esfera hay una vecindad con la que se puede identificar biholomórficamente . ${\displaystyle \mathbf {C} }$

Por otro lado, el teorema de uniformización , un resultado central en la clasificación de las superficies de Riemann, establece que toda superficie de Riemann simplemente conexa es biholomórfica con respecto al plano complejo, el plano hiperbólico o la esfera de Riemann. De ellas, la esfera de Riemann es la única que es una superficie cerrada (una superficie compacta sin límite ). De ahí que la esfera bidimensional admita una estructura compleja única convirtiéndola en una variedad compleja unidimensional.

Como la línea proyectiva compleja

La esfera de Riemann también puede definirse como la línea proyectiva compleja . Los puntos de la recta proyectiva compleja se pueden definir como clases de equivalencia de vectores no nulos en el espacio vectorial complejo : dos vectores no nulos y son equivalentes si y solo para algún coeficiente distinto de cero . ${\displaystyle \mathbf {C} ^{2}}$ ${\displaystyle (w,z)}$ ${\displaystyle (u,v)}$ ${\displaystyle (w,z)=(\lambda u,\lambda v)}$ ${\displaystyle \lambda \in \mathbf {C} }$

En este caso, la clase de equivalencia se escribe usando coordenadas proyectivas . Dado cualquier punto en la línea proyectiva compleja, uno de y debe ser distinto de cero, digamos . Luego por la noción de equivalencia, que está en un gráfico para la variedad de esferas de Riemann. ^[3] ${\displaystyle [w,z]}$ ${\displaystyle [w,z]}$ ${\displaystyle w}$ ${\displaystyle z}$ ${\displaystyle w\neq 0}$ ${\displaystyle [w,z]=\left[1,z/w\right]}$

Este tratamiento de la esfera de Riemann se conecta más fácilmente con la geometría proyectiva. Por ejemplo, cualquier línea (o cónica suave) en el plano proyectivo complejo es biholomórfica con respecto a la línea proyectiva compleja. También es conveniente para estudiar los automorfismos de la esfera , más adelante en este artículo.

como una esfera

Proyección estereográfica de un número complejo A sobre un punto α de la esfera de Riemann

La esfera de Riemann se puede visualizar como la esfera unitaria en el espacio real tridimensional . Para este fin, considere la proyección estereográfica desde la esfera unitaria menos el punto sobre el plano que identificamos con el plano complejo por . En coordenadas cartesianas y coordenadas esféricas sobre la esfera (con el cenit y el acimut ), la proyección es ${\displaystyle x^{2}+y^{2}+z^{2}=1}$ ${\displaystyle \mathbf {R} ^{3}}$ ${\displaystyle (0,0,1)}$ ${\displaystyle z=0,}$ ${\displaystyle \zeta =x+iy}$ ${\displaystyle (x,y,z)}$ ${\displaystyle (\theta ,\varphi )}$ ${\displaystyle \theta }$ ${\displaystyle \varphi }$

${\displaystyle \zeta ={\frac {x+iy}{1-z}}={\cot }{\bigl (}{\tfrac {1}{2}}\theta {\bigr )}\,e^{i\varphi }.}$

De manera similar, la proyección estereográfica desde el plano identificado con otra copia del plano complejo se escribe ${\displaystyle (0,0,-1)}$ ${\displaystyle z=0,}$ ${\displaystyle \xi =x-iy,}$

${\displaystyle \xi ={\frac {x-iy}{1+z}}={\tan }{\bigl (}{\tfrac {1}{2}}\theta {\bigr )}\,e^{-i\varphi }.}$

Las inversas de estas dos proyecciones estereográficas son mapas del plano complejo a la esfera. La primera inversa cubre la esfera excepto el punto , y la segunda cubre la esfera excepto el punto . Los dos planos complejos, que son los dominios de estos mapas, se identifican de manera diferente con el plano , porque es necesaria una inversión de orientación para mantener una orientación consistente en la esfera. ${\displaystyle (0,0,1)}$ ${\displaystyle (0,0,-1)}$ ${\displaystyle z=0}$

Los mapas de transición entre coordenadas - y - se obtienen componiendo una proyección con la inversa de la otra. Resultan ser y , como se describe anteriormente. Por tanto, la esfera unitaria es difeomorfa de la esfera de Riemann. ${\displaystyle \zeta }$ ${\displaystyle \xi }$ ${\displaystyle \zeta =1/\xi }$ ${\displaystyle \xi =1/\zeta }$

Bajo este difeomorfismo, se identifican el círculo unitario en el gráfico, el círculo unitario en el gráfico y el ecuador de la esfera unitaria. El disco unitario se identifica con el hemisferio sur , mientras que el disco unitario se identifica con el hemisferio norte . ${\displaystyle \zeta }$ ${\displaystyle \xi }$ ${\displaystyle |\zeta |<1}$ ${\displaystyle z<0}$ ${\displaystyle |\xi |<1}$ ${\displaystyle z>0}$

Métrico

Una superficie de Riemann no viene equipada con ninguna métrica riemanniana en particular . Sin embargo, la estructura conforme de la superficie de Riemann determina una clase de métricas: todas aquellas cuya estructura conforme subordinada es la dada. Más detalladamente: la compleja estructura de la superficie de Riemann determina de forma única una métrica hasta la equivalencia conforme . (Se dice que dos métricas son conformemente equivalentes si difieren mediante la multiplicación por una función suave positiva ). Por el contrario, cualquier métrica en una superficie orientada determina de forma única una estructura compleja, que depende de la métrica sólo hasta la equivalencia conforme. Por lo tanto, las estructuras complejas en una superficie orientada se corresponden uno a uno con clases conformes de métricas en esa superficie.

Dentro de una clase conforme dada, se puede utilizar la simetría conforme para encontrar una métrica representativa con propiedades convenientes. En particular, siempre hay una métrica completa con curvatura constante en cualquier clase conforme dada.

En el caso de la esfera de Riemann, el teorema de Gauss-Bonnet implica que una métrica de curvatura constante debe tener curvatura positiva . De ello se deduce que la métrica debe ser isométrica a la esfera de radio mediante proyección estereográfica. En el gráfico de la esfera de Riemann, la métrica con viene dada por ${\displaystyle K}$ ${\displaystyle 1/{\sqrt {K}}}$ ${\displaystyle \mathbf {R} ^{3}}$ ${\displaystyle \zeta }$ ${\displaystyle K=1}$

${\displaystyle ds^{2}=\left({\frac {2}{1+|\zeta |^{2}}}\right)^{2}\,|d\zeta |^{2}={\frac {4}{\left(1+\zeta {\overline {\zeta }}\right)^{2}}}\,d\zeta \,d{\overline {\zeta }}.}$

En coordenadas reales , la fórmula es ${\displaystyle \zeta =u+iv}$

${\displaystyle ds^{2}={\frac {4}{\left(1+u^{2}+v^{2}\right)^{2}}}\left(du^{2}+dv^{2}\right).}$

Hasta un factor constante, esta métrica concuerda con la métrica estándar de Fubini-Study sobre el espacio proyectivo complejo (de la cual la esfera de Riemann es un ejemplo).

Hasta la escala, esta es la única métrica en la esfera cuyo grupo de isometrías que preservan la orientación es tridimensional (y ninguna es más que tridimensional); ese grupo se llama En este sentido, ésta es, con diferencia, la métrica más simétrica de la esfera. (El grupo de todas las isometrías, conocido como , también es tridimensional, pero a diferencia no es un espacio conexo). ${\displaystyle {\mbox{SO}}(3)}$ ${\displaystyle {\mbox{O}}(3)}$ ${\displaystyle {\mbox{SO}}(3)}$

Por el contrario, denotemos la esfera (como una variedad topológica o suave abstracta ). Según el teorema de uniformización, existe una estructura compleja única hasta la equivalencia conforme. De ello se deduce que cualquier métrica es conformemente equivalente a la métrica redonda . Todas estas métricas determinan la misma geometría conforme. Por tanto, la métrica redonda no es intrínseca a la esfera de Riemann, ya que la "redondez" no es una invariante de la geometría conforme. La esfera de Riemann es sólo una variedad conforme , no una variedad de Riemann . Sin embargo, si uno necesita hacer geometría riemanniana en la esfera de Riemann, la métrica redonda es una opción natural (con cualquier radio fijo, aunque el radio es la opción más simple y común). Esto se debe a que sólo una métrica redonda en la esfera de Riemann tiene su grupo de isometría como un grupo tridimensional. (Es decir, el grupo conocido como , un grupo continuo ("Mentira") que topológicamente es el espacio proyectivo tridimensional ). ${\displaystyle S}$ ${\displaystyle S}$ ${\displaystyle S}$ ${\displaystyle 1}$ ${\displaystyle {\mbox{SO}}(3)}$ ${\displaystyle \mathbf {P} ^{3}}$

Automorfismos

Una transformación de Möbius que actúa sobre la esfera y sobre el plano mediante proyección estereográfica.

El estudio de cualquier objeto matemático se ve favorecido por la comprensión de su grupo de automorfismos, es decir, los mapas del objeto a sí mismo que preservan la estructura esencial del objeto. En el caso de la esfera de Riemann, un automorfismo es un mapa conforme invertible (es decir, mapa biholomórfico) de la esfera de Riemann a sí misma. Resulta que los únicos mapas de este tipo son las transformaciones de Möbius . Estas son funciones de la forma

${\displaystyle f(\zeta )={\frac {a\zeta +b}{c\zeta +d}},}$

donde , , y son números complejos tales que . Ejemplos de transformaciones de Möbius incluyen dilataciones , rotaciones , traslaciones e inversiones complejas. De hecho, cualquier transformación de Möbius puede escribirse como una composición de éstas. ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle d}$ ${\displaystyle ad-bc\neq 0}$

Las transformaciones de Möbius son homografías de la línea proyectiva compleja. En coordenadas proyectivas , la transformación f se puede escribir

${\displaystyle [\zeta ,\ 1]{\begin{pmatrix}a&c\\b&d\end{pmatrix}}\ =\ [a\zeta +b,\ c\zeta +d]\ =\ \left[{\tfrac {a\zeta +b}{c\zeta +d}},\ 1\right]\ =\ [f(\zeta ),\ 1].}$

Por tanto, las transformaciones de Möbius pueden describirse como matrices complejas de dos por dos con determinante distinto de cero . Dado que actúan sobre coordenadas proyectivas, dos matrices producen la misma transformación de Möbius si y sólo si difieren en un factor distinto de cero. El grupo de transformaciones de Möbius es el grupo lineal proyectivo . ${\displaystyle {\mbox{PGL}}(2,\mathbf {C} )}$

Si se dota a la esfera de Riemann de la métrica del estudio de Fubini , entonces no todas las transformaciones de Möbius son isometrías; por ejemplo, las dilataciones y traslaciones no lo son. Las isometrías forman un subgrupo propio de , a saber . Este subgrupo es isomorfo al grupo de rotación , que es el grupo de simetrías de la esfera unitaria en (que, cuando se restringen a la esfera, se convierten en las isometrías de la esfera). ${\displaystyle {\mbox{PGL}}(2,\mathbf {C} )}$ ${\displaystyle {\mbox{PSU}}(2)}$ ${\displaystyle {\mbox{SO}}(3)}$ ${\displaystyle \mathbf {R} ^{3}}$

Aplicaciones

En análisis complejo, una función meromorfa en el plano complejo (o en cualquier superficie de Riemann, de hecho) es una relación de dos funciones holomorfas y . Como mapa de números complejos, no está definido dondequiera que esté el cero. Sin embargo, induce un mapa holomórfico de la línea proyectiva compleja que está bien definida incluso donde . Esta construcción es útil en el estudio de funciones holomorfas y meromorfas. Por ejemplo, en una superficie compacta de Riemann no hay mapas holomorfos no constantes para los números complejos, pero abundan los mapas holomorfos para la línea proyectiva compleja. ${\displaystyle f/g}$ ${\displaystyle f}$ ${\displaystyle g}$ ${\displaystyle g}$ ${\displaystyle (f,g)}$ ${\displaystyle g=0}$

La esfera de Riemann tiene muchos usos en física. En mecánica cuántica, los puntos en la línea proyectiva compleja son valores naturales para los estados de polarización de fotones , los estados de espín de partículas masivas de espín y las partículas de 2 estados en general (ver también Bit cuántico y Esfera de Bloch ). La esfera de Riemann ha sido sugerida como modelo relativista de la esfera celeste . ^[4] En la teoría de cuerdas , las hojas de mundo de las cuerdas son superficies de Riemann, y la esfera de Riemann, al ser la superficie de Riemann más simple, juega un papel importante. También es importante en la teoría de los twistores . ${\displaystyle 1/2}$

Ver también

• Geometría conforme
• relación cruzada
• Diseño infantil
• Infinito dirigido
• paquete hopf
• Avión de Moebius
• Paralelo (operador) § Propiedades
• Línea real extendida proyectivamente
• carta de smith
• Teoría de la rueda

Referencias

1. B. Riemann: Theorie der Abel'sche Funktionen, J. Math. (Crelle) 1857; Obra 88-144. El nombre se debe a Neumann C:Vorlesungen über Riemanns Theorie der Abelsche Integrale, Leipzig 1865 (Teubner)
2. "C^*". Archivado desde el original el 8 de octubre de 2021 . Consultado el 12 de diciembre de 2021 .
3. William Mark Goldman (1999) Geometría hiperbólica compleja , página 1, Clarendon Press ISBN 0-19-853793-X 
4. R. Penrose (2007). El camino a la realidad . Libros antiguos. págs. 428–430 (§18.5). ISBN 978-0-679-77631-4.

• Brown, James y Churchill, Ruel (1989). Variables complejas y aplicaciones . Nueva York: McGraw-Hill. ISBN 0-07-010905-2.
• Griffiths, Phillip y Harris, Joseph (1978). Principios de Geometría Algebraica . John Wiley e hijos. ISBN 0-471-32792-1.
• Penrose, Roger (2005). El camino a la realidad . Nueva York: Knopf. ISBN 0-679-45443-8.
• Rudin, Walter (1987). Análisis Real y Complejo . Nueva York: McGraw-Hill. ISBN 0-07-100276-6.

enlaces externos

• "Esfera de Riemann", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Transformaciones de Moebius reveladas, de Douglas N. Arnold y Jonathan Rogness (un vídeo de dos profesores de la Universidad de Minnesota que explican e ilustran las transformaciones de Möbius mediante proyección estereográfica desde una esfera)