Esfera de colina

Región en la que un cuerpo astronómico domina la atracción de los satélites

En vista seccional/lateral, una representación bidimensional del concepto tridimensional de la esfera de Hill, que muestra aquí el "pozo de gravedad" de la Tierra (potencial gravitacional de la Tierra, línea azul), lo mismo para la Luna (línea roja) y su potencial combinado (línea gruesa negra). El punto P es el punto libre de fuerzas, donde las fuerzas gravitacionales de la Tierra y la Luna se cancelan. Los tamaños de la Tierra y la Luna están en proporción, pero las distancias y las energías no están a escala.

La esfera de Hill es un modelo común para el cálculo de una esfera de influencia gravitatoria . Es el modelo más comúnmente utilizado para calcular la extensión espacial de la influencia gravitatoria de un cuerpo astronómico ( m ) en el que domina sobre la influencia gravitatoria de otros cuerpos, particularmente un primario ( M ). ^[1] A veces se confunde con otros modelos de influencia gravitatoria, como la esfera de Laplace ^[1] o se la denomina esfera de Roche , esta última causando confusión con el límite de Roche . ^{[2] [3]} Fue definida por el astrónomo estadounidense George William Hill , basándose en el trabajo del astrónomo francés Édouard Roche . ^{[ no verificado en el cuerpo ]}

Para ser retenido por un objeto astrofísico que atraiga más gravitacionalmente (un planeta por una estrella más masiva, una luna por un planeta más masivo), el cuerpo menos masivo debe tener una órbita que se encuentre dentro del potencial gravitacional representado por la esfera de Hill del cuerpo más masivo. ^{[ no verificado en el cuerpo ]} Esa luna, a su vez, tendría una esfera de Hill propia, y cualquier objeto dentro de esa distancia tendería a convertirse en un satélite de la luna, en lugar del planeta mismo. ^{[ no verificado en el cuerpo ]}

Diagrama de contorno del potencial gravitacional efectivo de un sistema de dos cuerpos, aquí el Sol y la Tierra, que indica los cinco puntos de Lagrange . ^{[ aclaración necesaria ] [ cita necesaria ]}

Una visión simple de la extensión del Sistema Solar es que está limitado por la esfera de Hill del Sol (engendrada por la interacción del Sol con el núcleo galáctico u otras estrellas más masivas). ^{[4] [ verificación necesaria ]} Un ejemplo más complejo es el de la derecha, la esfera de Hill de la Tierra, que se extiende entre los puntos de Lagrange L 1 y L 2 , ^{[ aclaración necesaria ]} que se encuentran a lo largo de la línea de centros de la Tierra y el Sol más masivo. ^{[ no verificado en el cuerpo ]} La influencia gravitatoria del cuerpo menos masivo es menor en esa dirección, y por lo tanto actúa como el factor limitante para el tamaño de la esfera de Hill; ^{[ aclaración necesaria ]} más allá de esa distancia, un tercer objeto en órbita alrededor de la Tierra pasaría al menos parte de su órbita fuera de la esfera de Hill, y sería perturbado progresivamente por las fuerzas de marea del cuerpo más masivo, el Sol, terminando eventualmente orbitando este último. ^{[ no verificado en el cuerpo ]}

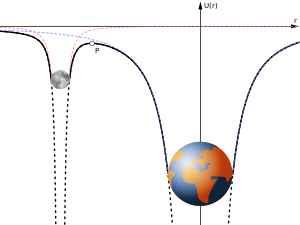
Para dos cuerpos masivos con potenciales gravitacionales y cualquier energía dada de un tercer objeto de masa despreciable que interactúa con ellos, se puede definir una superficie de velocidad cero en el espacio que no se puede pasar, el contorno de la integral de Jacobi . ^{[ no verificado en el cuerpo ]} Cuando la energía del objeto es baja, la superficie de velocidad cero rodea completamente al cuerpo menos masivo (de este sistema restringido de tres cuerpos ), lo que significa que el tercer objeto no puede escapar; a mayor energía, habrá uno o más huecos o cuellos de botella por los cuales el tercer objeto puede escapar del cuerpo menos masivo y entrar en órbita alrededor del más masivo. ^{[ no verificado en el cuerpo ]} Si la energía está en el límite entre estos dos casos, entonces el tercer objeto no puede escapar, pero la superficie de velocidad cero que lo confina toca una superficie de velocidad cero más grande alrededor del cuerpo menos masivo ^{[ verificación necesaria ]} en uno de los puntos de Lagrange cercanos, formando allí un punto en forma de cono. ^{[ aclaración necesaria ] [ no verificado en el cuerpo ]} En el lado opuesto del cuerpo menos masivo, la superficie de velocidad cero se acerca al otro punto de Lagrange. ^{[ no verificado en el cuerpo ]}

Definición

El radio o esfera de Hill (este último definido por el radio anterior ^{[ cita requerida ]} ) se ha descrito como "la región alrededor de un cuerpo planetario donde su propia gravedad (en comparación con la del Sol u otros cuerpos cercanos) es la fuerza dominante en la atracción de satélites", tanto naturales como artificiales. ^{[5] [ se necesita una mejor fuente ]}

Como lo describen de Pater y Lissauer, todos los cuerpos dentro de un sistema como el Sistema Solar del Sol "sienten la fuerza gravitatoria de los demás", y mientras que los movimientos de sólo dos cuerpos que interactúan gravitatoriamente -lo que constituye un "problema de dos cuerpos"- son "completamente integrables ([lo que significa]... que existe una integral o restricción independiente por grado de libertad)" y, por lo tanto, una solución analítica exacta, las interacciones de tres (o más) de esos cuerpos "no pueden deducirse analíticamente", requiriendo en cambio soluciones por integración numérica, cuando sea posible. ^{[6] : p.26} Este es el caso, a menos que la masa despreciable de uno de los tres cuerpos permita la aproximación del sistema como un problema de dos cuerpos, conocido formalmente como un "problema restringido de tres cuerpos". ^{[6] : p.26}

Para problemas de dos o tres cuerpos restringidos como sus ejemplos más simples (por ejemplo, un cuerpo astrofísico primario más masivo, masa m1, y un cuerpo secundario menos masivo, masa m2), el concepto de radio o esfera de Hill es el límite aproximado de la "dominación gravitacional" de la masa secundaria, ^[6] un límite definido por "la extensión" de su esfera de Hill, que se representa matemáticamente de la siguiente manera: ^{[6] : p.29  [7]}

${\displaystyle R_{\mathrm {H} }\approx a{\sqrt[{3}]{\frac {m_{2}}{3(m_{1}+m_{2})}}}}$,

donde, en esta representación, el eje mayor "a" puede entenderse como la "distancia heliocéntrica instantánea" entre las dos masas (abreviada en otros lugares como r p ). ^{[6] : p.29  [7]}

De manera más general, si el cuerpo menos masivo, , orbita alrededor de un cuerpo más masivo (m1, por ejemplo, como un planeta que orbita alrededor del Sol) y tiene un semieje mayor , y una excentricidad de , entonces el radio de Hill o esfera, del cuerpo menos masivo, calculado en el pericentro , es aproximadamente: ^{[8] [ se necesita una fuente no primaria ] [ se necesita una mejor fuente ]} ${\displaystyle m2}$ ${\displaystyle a}$ ${\displaystyle e}$ ${\displaystyle R_{\mathrm {H} }}$

${\displaystyle R_{\mathrm {H} }\approx a(1-e){\sqrt[{3}]{\frac {m_{2}}{3(m_{1}+m_{2})}}}.}$

Cuando la excentricidad es despreciable (el caso más favorable para la estabilidad orbital), esta expresión se reduce a la presentada anteriormente. ^{[ cita requerida ]}

Ejemplo y derivación

Representación esquemática, no a escala, de las esferas de Hill (como radios 2D) y los límites de Roche de cada cuerpo del sistema Sol-Tierra-Luna. El radio real de Hill para el par Tierra-Luna es del orden de 60.000 km (es decir, se extiende menos de una sexta parte de la distancia de los 378.000 km entre la Luna y la Tierra). ^[9]

En el ejemplo de la Tierra y el Sol, la Tierra (5,97 × 10 ²⁴  kg ) orbita alrededor del Sol (1,99 × 10 ³⁰  kg ) a una distancia de 149,6 millones de kilómetros, o una unidad astronómica (UA). La esfera de Hill de la Tierra se extiende, por tanto, hasta unos 1,5 millones de kilómetros (0,01 UA). La órbita de la Luna, a una distancia de 0,384 millones de kilómetros de la Tierra, se encuentra cómodamente dentro de la esfera de influencia gravitatoria de la Tierra y, por tanto, no corre el riesgo de ser arrastrada a una órbita independiente alrededor del Sol.

La fórmula anterior que ignora la excentricidad se puede reformular de la siguiente manera:

${\displaystyle {\frac {R_{\mathrm {H} }^{3}}{a^{3}}}\approx 1/3{\frac {m2}{M}}}$, o , ${\displaystyle 3{\frac {R_{\mathrm {H} }^{3}}{a^{3}}}\approx {\frac {m2}{M}}}$

donde M es la suma de las masas que interactúan.

Derivación

La expresión para el radio de Hill se puede encontrar igualando las fuerzas gravitacionales y centrífugas que actúan sobre una partícula de prueba (de masa mucho menor que ) que orbita alrededor del cuerpo secundario. Suponga que la distancia entre las masas y es , y que la partícula de prueba está orbitando a una distancia del cuerpo secundario. Cuando la partícula de prueba está en la línea que conecta el cuerpo primario y el secundario, el equilibrio de fuerzas requiere que ${\displaystyle m}$ ${\displaystyle M}$ ${\displaystyle m}$ ${\displaystyle r}$ ${\displaystyle r_{\mathrm {H} }}$

${\displaystyle {\frac {Gm}{r_{\mathrm {H} }^{2}}}-{\frac {GM}{(r-r_{\mathrm {H} })^{2}}}+\Omega ^{2}(r-r_{\mathrm {H} })=0,}$

donde es la constante gravitacional y es la velocidad angular ( kepleriana ) del secundario respecto del primario (suponiendo que ). La ecuación anterior también se puede escribir como ${\displaystyle G}$ ${\displaystyle \Omega ={\sqrt {\frac {GM}{r^{3}}}}}$ ${\displaystyle m\ll M}$

${\displaystyle {\frac {m}{r_{\mathrm {H} }^{2}}}-{\frac {M}{r^{2}}}\left(1-{\frac {r_{\mathrm {H} }}{r}}\right)^{-2}+{\frac {M}{r^{2}}}\left(1-{\frac {r_{\mathrm {H} }}{r}}\right)=0,}$

que, a través de una expansión binomial hasta el orden principal en , se puede escribir como ${\displaystyle r_{\mathrm {H} }/r}$

${\displaystyle {\frac {m}{r_{\mathrm {H} }^{2}}}-{\frac {M}{r^{2}}}\left(1+2{\frac {r_{\mathrm {H} }}{r}}\right)+{\frac {M}{r^{2}}}\left(1-{\frac {r_{\mathrm {H} }}{r}}\right)={\frac {m}{r_{\mathrm {H} }^{2}}}-{\frac {M}{r^{2}}}\left(3{\frac {r_{\mathrm {H} }}{r}}\right)\approx 0.}$

Por lo tanto, la relación establecida anteriormente

${\displaystyle {\frac {r_{\mathrm {H} }}{r}}\approx {\sqrt[{3}]{\frac {m}{3M}}}.}$

Si la órbita del secundario en torno al primario es elíptica, el radio de Hill es máximo en el apocentro , donde es mayor, y mínimo en el pericentro de la órbita. Por lo tanto, a los efectos de la estabilidad de las partículas de prueba (por ejemplo, de los satélites pequeños), se debe considerar el radio de Hill en la distancia del pericentro. ${\displaystyle r}$

Para el orden principal en , el radio de Hill anterior también representa la distancia del punto lagrangiano L ₁ desde el secundario. ${\displaystyle r_{\mathrm {H} }/r}$

Regiones de estabilidad

La esfera de Hill es sólo una aproximación, y otras fuerzas (como la presión de radiación o el efecto Yarkovsky ) pueden eventualmente perturbar un objeto fuera de la esfera. ^{[ cita requerida ]} Como se dijo, el satélite (tercera masa) debería ser lo suficientemente pequeño como para que su gravedad contribuya de manera insignificante. ^{[6] : p.26ff}

Los cálculos numéricos detallados muestran que las órbitas en la esfera de Hill o justo dentro de ella no son estables en el largo plazo; parece que las órbitas estables de los satélites existen sólo dentro de 1/2 a 1/3 del radio de Hill. ^{[ cita requerida ]}

La región de estabilidad para órbitas retrógradas a gran distancia de la primaria es mayor que la región para órbitas progradas a gran distancia de la primaria. Se pensaba que esto explicaba la preponderancia de lunas retrógradas alrededor de Júpiter; sin embargo, Saturno tiene una mezcla más uniforme de lunas retrógradas/progradas, por lo que las razones son más complicadas. ^[10]

Más ejemplos

Es posible que una esfera de Hill sea tan pequeña que sea imposible mantener una órbita alrededor de un cuerpo. Por ejemplo, un astronauta no podría haber orbitado el transbordador espacial de 104 toneladas en una órbita a 300 km sobre la Tierra, porque un objeto de 104 toneladas a esa altitud tiene una esfera de Hill de solo 120 cm de radio, mucho más pequeña que un transbordador espacial. Una esfera de este tamaño y masa sería más densa que el plomo y, de hecho, en la órbita terrestre baja , un cuerpo esférico debe ser más denso que el plomo para caber dentro de su propia esfera de Hill, o de lo contrario será incapaz de mantener una órbita. Los satélites más alejados en la órbita geoestacionaria , sin embargo, solo necesitarían tener más del 6% de la densidad del agua para caber dentro de su propia esfera de Hill. ^{[ cita requerida ]}

Dentro del Sistema Solar , el planeta con el mayor radio de Hill es Neptuno , con 116 millones de km, o 0,775 ua; su gran distancia del Sol compensa ampliamente su pequeña masa en relación con Júpiter (cuyo propio radio de Hill mide 53 millones de km). Un asteroide del cinturón de asteroides tendrá una esfera de Hill que puede alcanzar los 220.000 km (para 1 Ceres ), disminuyendo rápidamente con la disminución de la masa. La esfera de Hill de 66391 Moshup , un asteroide que cruza Mercurio y que tiene una luna (llamada Squannit), mide 22 km de radio. ^[11]

Un típico " Júpiter caliente " extrasolar , HD 209458 b , ^[12] tiene un radio de esfera de Hill de 593.000 km, aproximadamente ocho veces su radio físico de aproximadamente 71.000 km. Incluso el planeta extrasolar cercano más pequeño, CoRoT-7b , ^[13] aún tiene un radio de esfera de Hill (61.000 km), seis veces su radio físico (aproximadamente 10.000 km). Por lo tanto, estos planetas podrían tener pequeñas lunas cercanas, aunque no dentro de sus respectivos límites de Roche . ^{[ cita requerida ]}

Esferas de colinas para el sistema solar

La siguiente tabla y gráfico logarítmico muestran el radio de las esferas de Hill de algunos cuerpos del Sistema Solar calculados con la primera fórmula mencionada anteriormente (incluyendo la excentricidad orbital), utilizando valores obtenidos de las efemérides del JPL DE405 y del sitio web de Exploración del Sistema Solar de la NASA. ^[14]

Gráfico logarítmico de los radios de Hill (en km) para los cuerpos del sistema solar

Véase también

• Esfera de Laplace
• Red de transporte interplanetario
• Problema de n -cuerpos
• Lóbulo de Roche
• Esfera de influencia (astrodinámica)
• Esfera de influencia (agujero negro)

Notas explicativas

1. A una distancia promedio, visto desde el Sol. El tamaño angular visto desde la Tierra varía dependiendo de la proximidad de la Tierra al objeto.

Referencias

1. Souami, D.; Cresson, J.; Biernacki, C.; Pierret, F. (2020). "Sobre las propiedades locales y globales de las esferas de influencia gravitacionales". Avisos mensuales de la Real Sociedad Astronómica . 496 (4): 4287–4297. arXiv : 2005.13059 . doi : 10.1093/mnras/staa1520 .
2. Williams, Matt (30 de diciembre de 2015). "¿Cuántas lunas tiene Mercurio?". Universe Today . Consultado el 8 de noviembre de 2023 .
3. Hill, Roderick J. (2022). "Despeje gravitacional de las órbitas de los satélites naturales". Publicaciones de la Sociedad Astronómica de Australia . 39 . Cambridge University Press. Bibcode :2022PASA...39....6H. doi :10.1017/pasa.2021.62. ISSN  1323-3580. S2CID  246637375.
4. Chebotarev, GA (marzo de 1965). "Sobre los límites dinámicos del sistema solar". Astronomía soviética . 8 : 787. Código Bibliográfico :1965SvA.....8..787C.
5. Lauretta, Dante y el personal de la misión de devolución de muestras del asteroide Osiris-Rex (2023). "Palabra de la semana: Hill Sphere". Misión de retorno de muestras del asteroide Osiris-Rex (AsteroidMission.org) . Tempe, AZ: Universidad de Arizona . Consultado el 22 de julio de 2023 .
6. de Pater, Imke y Lissauer, Jack (2015). "Dinámica (El problema de los tres cuerpos, perturbaciones y resonancias)". Ciencias planetarias (2.ª ed.). Cambridge, Inglaterra: Cambridge University Press. pp. 26, 28–30, 34. ISBN 9781316195697. Recuperado el 22 de julio de 2023 .{{cite book}}: CS1 maint: multiple names: authors list (link)
7. Higuchi1, A. & Ida, S. (abril de 2017). "Captura temporal de asteroides por un planeta excéntrico". The Astronomical Journal . 153 (4). Washington, DC: The American Astronomical Society: 155. arXiv : 1702.07352 . Bibcode :2017AJ....153..155H. doi : 10.3847/1538-3881/aa5daa . S2CID  119036212.{{cite journal}}: CS1 maint: multiple names: authors list (link) CS1 maint: numeric names: authors list (link)
8. Hamilton, DP y Burns, JA (marzo de 1992). "Zonas de estabilidad orbital sobre asteroides: II. Los efectos desestabilizadores de las órbitas excéntricas y de la radiación solar". Icarus . 96 (1). Nueva York, NY: Academic Press: 43–64. Bibcode :1992Icar...96...43H. doi : 10.1016/0019-1035(92)90005-R .{{cite journal}}: CS1 maint: multiple names: authors list (link)Véase también Hamilton, DP y Burns, JA (marzo de 1991). "Orbital Stability Zones About Asteroids" (PDF) . Icarus . 92 (1). Nueva York, NY: Academic Press: 118–131. Bibcode :1991Icar...92..118H. doi :10.1016/0019-1035(91)90039-V . Consultado el 22 de julio de 2023 .{{cite journal}}: CS1 maint: multiple names: authors list (link)citado en el mismo.
9. Follows, Mike (4 de octubre de 2017). "Círculos cada vez más pequeños". NewScientist.com . Consultado el 23 de julio de 2023. La esfera de Hill de la Luna tiene un radio de 60.000 kilómetros, aproximadamente una sexta parte de la distancia entre ella y la Tierra.
10. Astakhov, Sergey A.; Burbanks, Andrew D.; Wiggins, Stephen y Farrelly, David (2003). "Captura de lunas irregulares asistida por el caos". Nature . 423 (6937): 264–267. Bibcode :2003Natur.423..264A. doi :10.1038/nature01622. PMID  12748635. S2CID  16382419.
11. Johnston, Robert (20 de octubre de 2019). «(66391) Moshup and Squannit». Archivo de Johnston . Consultado el 30 de marzo de 2017 .
12. "HD 209458 b". Enciclopedia de planetas extrasolares . Archivado desde el original el 16 de enero de 2010. Consultado el 16 de febrero de 2010 .
13. "Planeta CoRoT-7 b". Enciclopedia de planetas extrasolares . 2024.
14. "Exploración del sistema solar de la NASA". NASA . Consultado el 22 de diciembre de 2020 .

Lectura adicional

• de Pater, Imke y Lissauer, Jack (2015). "Dinámica (El problema de los tres cuerpos, perturbaciones y resonancias)". Ciencias planetarias (2.ª ed.). Cambridge, Inglaterra: Cambridge University Press. pp. 28–30, 34. ISBN 9781316195697. Recuperado el 22 de julio de 2023 .{{cite book}}: CS1 maint: multiple names: authors list (link)
• de Pater, Imke y Lissauer, Jack (2015). "Formación de planetas (formación de planetas gigantes, satélites de planetas y planetas menores)". Ciencias planetarias (2.ª ed.). Cambridge, Inglaterra: Cambridge University Press. pp. 539, 544. ISBN 9781316195697. Recuperado el 22 de julio de 2023 .{{cite book}}: CS1 maint: multiple names: authors list (link)
• Gurzadyan, Grigor A. (2020). "La esfera de atracción, la esfera de acción y la esfera de Hill". Teoría de los vuelos interplanetarios. Boca Raton, FL: CRC Press. pp. 258–263. ISBN 9781000116717. Recuperado el 22 de julio de 2023 .
• Gurzadyan, Grigor A. (2020). "El límite de Roche". Teoría de los vuelos interplanetarios. Boca Raton, FL: CRC Press. pp. 263f. ISBN 9781000116717. Recuperado el 22 de julio de 2023 .
• Ida, S.; Kokubo, E. y Takeda, T. (2012). "Simulaciones de acreción lunar con N cuerpos". En Marov, Mikhail Ya. y Rickman, Hans (ed.). Procesos de colisión en el sistema solar. Biblioteca de Astrofísica y Ciencia Espacial. Vol. 261. Berlín, Alemania: Springer Science & Business Media. págs. 206, 209f. ISBN. 9789401007122. Recuperado el 22 de julio de 2023 .{{cite book}}: CS1 maint: multiple names: authors list (link)
• Ip, W.-H. y Fernandez, JA (2012). "Origen acrecional de los planetas gigantes y sus consecuencias". En Marov, Mikhail Ya. y Rickman, Hans (ed.). Procesos de colisión en el sistema solar. Biblioteca de Astrofísica y Ciencia Espacial. Vol. 261. Berlín, Alemania: Springer Science & Business Media. pp. 173f. ISBN. 9789401007122. Recuperado el 22 de julio de 2023 .{{cite book}}: CS1 maint: multiple names: authors list (link)
• Asher, DJ; Bailey, ME y Steel (2012). "El papel de las fuerzas no gravitacionales en el desacoplamiento de las órbitas de Júpiter". En Marov, Mikhail Ya. y Rickman, Hans (ed.). Procesos de colisión en el sistema solar. Biblioteca de Astrofísica y Ciencia Espacial. Vol. 261. Berlín, Alemania: Springer Science & Business Media. pág. 122. ISBN. 9789401007122. Recuperado el 22 de julio de 2023 .{{cite book}}: CS1 maint: multiple names: authors list (link)

Enlaces externos

• ¿Puede un astronauta orbitar el transbordador espacial?
• La luna que subió una colina, pero bajó un planeta Archivado el 30 de septiembre de 2008 en Wayback Machine.