Teorema fundamental del cálculo

Relación entre derivadas e integrales

El teorema fundamental del cálculo es un teorema que vincula el concepto de diferenciar una función (calcular sus pendientes o tasa de cambio en cada punto del tiempo) con el concepto de integrar una función (calcular el área bajo su gráfica o el efecto acumulativo de pequeñas contribuciones). En términos generales, las dos operaciones pueden considerarse como inversas entre sí.

La primera parte del teorema, el primer teorema fundamental del cálculo , establece que para una función continua f , una antiderivada o integral indefinida F puede obtenerse como la integral de f en un intervalo con un límite superior variable. ^[1]

Por el contrario, la segunda parte del teorema, el segundo teorema fundamental del cálculo , establece que la integral de una función f en un intervalo fijo es igual al cambio de cualquier antiderivada F entre los extremos del intervalo. Esto simplifica enormemente el cálculo de una integral definida siempre que se pueda hallar una antiderivada mediante integración simbólica , evitando así la integración numérica .

Historia

El teorema fundamental del cálculo relaciona la diferenciación y la integración, mostrando que estas dos operaciones son esencialmente inversas entre sí. Antes del descubrimiento de este teorema, no se reconocía que estas dos operaciones estuvieran relacionadas. Los matemáticos de la antigua Grecia sabían cómo calcular el área mediante infinitesimales , una operación que ahora llamaríamos integración. Los orígenes de la diferenciación también son anteriores al teorema fundamental del cálculo por cientos de años; por ejemplo, en el siglo XIV las nociones de continuidad de funciones y movimiento fueron estudiadas por los Calculadores de Oxford y otros eruditos. La relevancia histórica del teorema fundamental del cálculo no es la capacidad de calcular estas operaciones, sino la comprensión de que las dos operaciones aparentemente distintas (cálculo de áreas geométricas y cálculo de gradientes) en realidad están estrechamente relacionadas.

A partir de la conjetura y la demostración del teorema fundamental del cálculo, se inicia el cálculo como una teoría unificada de integración y diferenciación. El primer enunciado y demostración publicados de una forma rudimentaria del teorema fundamental, de carácter marcadamente geométrico, ^[2] fue obra de James Gregory (1638-1675). ^{[3] [4]} Isaac Barrow (1630-1677) demostró una versión más generalizada del teorema, ^[5] mientras que su alumno Isaac Newton (1642-1727) completó el desarrollo de la teoría matemática circundante. Gottfried Leibniz (1646-1716) sistematizó el conocimiento en un cálculo para cantidades infinitesimales e introdujo la notación que se utiliza hoy en día.

Significado geométrico/Prueba

El área sombreada con rayas rojas es cercana a h multiplicada por f ( x ) . Alternativamente, si se conociera la función A ( x ) , esta área sería exactamente A ( x + h ) − A ( x ) . Estos dos valores son aproximadamente iguales, particularmente para valores h pequeños .

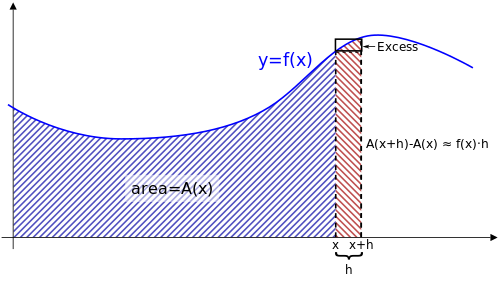
El primer teorema fundamental puede interpretarse de la siguiente manera: dada una función continua cuyo gráfico se representa como una curva, se define una "función de área" correspondiente tal que A ( x ) es el área debajo de la curva entre 0 y x . El área A ( x ) puede no ser fácil de calcular, pero se supone que está bien definida. ${\displaystyle y=f(x)}$ ${\displaystyle x\mapsto A(x)}$

El área bajo la curva entre x y x + h se puede calcular hallando el área entre 0 y x + h y luego restando el área entre 0 y x . En otras palabras, el área de esta "franja" sería A ( x + h ) − A ( x ) .

Hay otra forma de estimar el área de esta misma franja. Como se muestra en la figura adjunta, h se multiplica por f ( x ) para hallar el área de un rectángulo que tiene aproximadamente el mismo tamaño que esta franja. Por lo tanto: $${\displaystyle A(x+h)-A(x)\approx f(x)\cdot h}$$

Dividiendo por h en ambos lados, obtenemos: $${\displaystyle {\frac {A(x+h)-A(x)}{h}}\ \approx f(x)}$$

Esta estimación se convierte en una igualdad perfecta cuando h se acerca a 0: es decir, la derivada de la función de área A ( x ) existe y es igual a la función original f ( x ) , por lo que la función de área es una antiderivada de la función original. $${\displaystyle f(x)=\lim _{h\to 0}{\frac {A(x+h)-A(x)}{h}}\ {\stackrel {\text{def}}{=}}\ A'(x).}$$

Así, la derivada de la integral de una función (el área) es la función original, de modo que derivada e integral son operaciones inversas que se invierten entre sí. Esta es la esencia del Teorema Fundamental.

Intuición física

Intuitivamente, el teorema fundamental establece que la integración y la diferenciación son operaciones inversas que se invierten entre sí.

El segundo teorema fundamental dice que la suma de los cambios infinitesimales en una cantidad (la integral de la derivada de la cantidad) se suma al cambio neto en la cantidad. Para visualizar esto, imagina que viajas en un automóvil y quieres saber la distancia recorrida (el cambio neto en la posición a lo largo de la carretera). Puedes ver la velocidad en el velocímetro, pero no puedes mirar hacia afuera para ver tu ubicación. Cada segundo, puedes encontrar qué tan lejos ha viajado el automóvil usando distancia = velocidad × tiempo , es decir, multiplicando la velocidad actual (en kilómetros o millas por hora) por el intervalo de tiempo (1 segundo = hora). Sumando todos estos pequeños pasos, puedes aproximar la distancia total recorrida, a pesar de no mirar fuera del automóvil: Como se vuelve infinitesimalmente pequeño, la suma corresponde a la integración . Por lo tanto, la integral de la función de velocidad (la derivada de la posición) calcula qué tan lejos ha viajado el automóvil (el cambio neto en la posición). ${\displaystyle {\tfrac {1}{3600}}}$ $${\displaystyle {\text{distance traveled}}=\sum \left({\begin{array}{c}{\text{velocity at}}\\{\text{each time}}\end{array}}\right)\times \left({\begin{array}{c}{\text{time}}\\{\text{interval}}\end{array}}\right)=\sum v_{t}\times \Delta t.}$$ ${\displaystyle \Delta t}$

El primer teorema fundamental dice que el valor de cualquier función es la tasa de cambio (la derivada) de su integral desde un punto de partida fijo hasta cualquier punto final elegido. Continuando con el ejemplo anterior utilizando una velocidad como función, puede integrarla desde el tiempo de partida hasta cualquier tiempo dado para obtener una función de distancia cuya derivada sea esa velocidad. (Para obtener la posición de su marcador de carretera, necesitaría sumar su posición de partida a esta integral y tener en cuenta si su viaje fue en la dirección de los marcadores de millas crecientes o decrecientes).

Declaraciones formales

El teorema consta de dos partes: la primera trata de la derivada de una antiderivada , mientras que la segunda trata de la relación entre las antiderivadas y las integrales definidas .

Primera parte

Esta parte a veces se denomina el primer teorema fundamental del cálculo . ^[6]

Sea f una función continua de valor real definida en un intervalo cerrado [ a , b ] . Sea F la función definida, para todo x en [ a , b ] , por $${\displaystyle F(x)=\int _{a}^{x}f(t)\,dt.}$$

Entonces F es uniformemente continua en [ a , b ] y diferenciable en el intervalo abierto ( a , b ) , y para todo x en ( a , b ) entonces F es una antiderivada de f . $${\displaystyle F'(x)=f(x)}$$

Corolario

Teorema fundamental del cálculo (animación)

El teorema fundamental se emplea a menudo para calcular la integral definida de una función para la que se conoce una antiderivada. En concreto, si es una función continua de valor real en y es una antiderivada de en , entonces ${\displaystyle f}$ ${\displaystyle F}$ ${\displaystyle f}$ ${\displaystyle [a,b]}$ ${\displaystyle F}$ ${\displaystyle f}$ ${\displaystyle [a,b]}$ $${\displaystyle \int _{a}^{b}f(t)\,dt=F(b)-F(a).}$$

El corolario supone continuidad en todo el intervalo. Este resultado se refuerza ligeramente en la siguiente parte del teorema.

Segunda parte

Esta parte a veces se denomina el segundo teorema fundamental del cálculo ^[7] o el teorema de Newton-Leibniz .

Sea una función de valor real en un intervalo cerrado y una función continua en la que es una antiderivada de en : ${\displaystyle f}$ ${\displaystyle [a,b]}$ ${\displaystyle F}$ ${\displaystyle [a,b]}$ ${\displaystyle f}$ ${\displaystyle (a,b)}$ $${\displaystyle F'(x)=f(x).}$$

Si es Riemann integrable en entonces ${\displaystyle f}$ ${\displaystyle [a,b]}$ $${\displaystyle \int _{a}^{b}f(x)\,dx=F(b)-F(a).}$$

La segunda parte es algo más fuerte que el corolario porque no supone que sea continuo. ${\displaystyle f}$

Cuando existe una antiderivada de , entonces hay infinitas antiderivadas para , que se obtienen sumando una constante arbitraria a . Además, por la primera parte del teorema, siempre existen antiderivadas de cuando es continua. ${\displaystyle F}$ ${\displaystyle f}$ ${\displaystyle f}$ ${\displaystyle F}$ ${\displaystyle f}$ ${\displaystyle f}$

Prueba de la primera parte

Para una función dada f , defina la función F ( x ) como $${\displaystyle F(x)=\int _{a}^{x}f(t)\,dt.}$$

Para cualesquiera dos números x ₁ y x ₁ + Δ x en [ a , b ] , tenemos

$${\displaystyle {\begin{aligned}F(x_{1}+\Delta x)-F(x_{1})&=\int _{a}^{x_{1}+\Delta x}f(t)\,dt-\int _{a}^{x_{1}}f(t)\,dt\\&=\int _{x_{1}}^{x_{1}+\Delta x}f(t)\,dt,\end{aligned}}}$$La última igualdad resulta de las propiedades básicas de las integrales y de la aditividad de las áreas.

Según el teorema del valor medio para la integración , existe un número real tal que ${\displaystyle c\in [x_{1},x_{1}+\Delta x]}$ $${\displaystyle \int _{x_{1}}^{x_{1}+\Delta x}f(t)\,dt=f(c)\cdot \Delta x.}$$

De ello se deduce que y por lo tanto que $${\displaystyle F(x_{1}+\Delta x)-F(x_{1})=f(c)\cdot \Delta x,}$$ $${\displaystyle {\frac {F(x_{1}+\Delta x)-F(x_{1})}{\Delta x}}=f(c).}$$

Tomando el límite como y teniendo en cuenta que se obtiene que es, según la definición de la derivada, la continuidad de f , y el teorema del apretón . ^[8] ${\displaystyle \Delta x\to 0,}$ ${\displaystyle c\in [x_{1},x_{1}+\Delta x],}$ $${\displaystyle \lim _{\Delta x\to 0}{\frac {F(x_{1}+\Delta x)-F(x_{1})}{\Delta x}}=\lim _{\Delta x\to 0}f(c),}$$ $${\displaystyle F'(x_{1})=f(x_{1}),}$$

Prueba del corolario

Supóngase que F es una antiderivada de f , con f continua en [ a , b ] . Sea $${\displaystyle G(x)=\int _{a}^{x}f(t)\,dt.}$$

Por la primera parte del teorema, sabemos que G también es una antiderivada de f . Como F ′ − G ′ = 0 el teorema del valor medio implica que F − G es una función constante , es decir, hay un número c tal que G ( x ) = F ( x ) +  c para todo x en [ a , b ] . Si x = a , tenemos que significa que c = − F ( a ) . En otras palabras, G ( x ) = F ( x ) − F ( a ) , y por lo tanto $${\displaystyle F(a)+c=G(a)=\int _{a}^{a}f(t)\,dt=0,}$$ $${\displaystyle \int _{a}^{b}f(x)\,dx=G(b)=F(b)-F(a).}$$

Prueba de la segunda parte

Esta es una prueba límite mediante sumas de Riemann .

Para empezar, recordemos el teorema del valor medio . Dicho brevemente, si F es continua en el intervalo cerrado [ a , b ] y diferenciable en el intervalo abierto ( a , b ) , entonces existe algún c en ( a , b ) tal que $${\displaystyle F'(c)(b-a)=F(b)-F(a).}$$

Sea f integrable (Riemann) en el intervalo [ a , b ] , y sea f admitiendo una antiderivada F en ( a , b ) tal que F sea continua en [ a , b ] . Comencemos con la cantidad F ( b ) − F ( a ) . Sean números x ₀ , ..., x _n tales que $${\displaystyle a=x_{0}<x_{1}<x_{2}<\cdots <x_{n-1}<x_{n}=b.}$$

Resulta que $${\displaystyle F(b)-F(a)=F(x_{n})-F(x_{0}).}$$

Ahora, sumamos cada F ( x _i ) junto con su inverso aditivo, de modo que la cantidad resultante sea igual: $${\displaystyle {\begin{aligned}F(b)-F(a)&=F(x_{n})+[-F(x_{n-1})+F(x_{n-1})]+\cdots +[-F(x_{1})+F(x_{1})]-F(x_{0})\\&=[F(x_{n})-F(x_{n-1})]+[F(x_{n-1})-F(x_{n-2})]+\cdots +[F(x_{2})-F(x_{1})]+[F(x_{1})-F(x_{0})].\end{aligned}}}$$

La cantidad anterior se puede escribir como la siguiente suma:

La función F es diferenciable en el intervalo ( a , b ) y continua en el intervalo cerrado [ a , b ] ; por lo tanto, también es diferenciable en cada intervalo ( x _{i −1} , x _i ) y continua en cada intervalo [ x _{i −1} , x _i ] . De acuerdo con el teorema del valor medio (arriba), para cada i existe un en ( x _{i −1} , x _i ) tal que ${\displaystyle c_{i}}$ $${\displaystyle F(x_{i})-F(x_{i-1})=F'(c_{i})(x_{i}-x_{i-1}).}$$

Sustituyendo lo anterior en ( 1' ), obtenemos $${\displaystyle F(b)-F(a)=\sum _{i=1}^{n}[F'(c_{i})(x_{i}-x_{i-1})].}$$

El supuesto implica También, puede expresarse como de partición . ${\displaystyle F'(c_{i})=f(c_{i}).}$ ${\displaystyle x_{i}-x_{i-1}}$ ${\displaystyle \Delta x}$ ${\displaystyle i}$

Una secuencia convergente de sumas de Riemann. El número en la esquina superior izquierda es el área total de los rectángulos azules. Convergen a la integral definida de la función.

Estamos describiendo el área de un rectángulo, multiplicando el ancho por la altura, y sumando las áreas. Cada rectángulo, en virtud del teorema del valor medio , describe una aproximación de la sección de la curva sobre la que se dibuja. Además, no es necesario que sea el mismo para todos los valores de i , o en otras palabras, el ancho de los rectángulos puede diferir. Lo que tenemos que hacer es aproximar la curva con n rectángulos. Ahora, a medida que el tamaño de las particiones se hace más pequeño y n aumenta, lo que da como resultado más particiones para cubrir el espacio, nos acercamos cada vez más al área real de la curva. ${\displaystyle \Delta x_{i}}$

Al tomar el límite de la expresión cuando la norma de las particiones se acerca a cero, llegamos a la integral de Riemann . Sabemos que este límite existe porque se supuso que f era integrable. Es decir, tomamos el límite cuando la mayor de las particiones se acerca a cero en tamaño, de modo que todas las demás particiones son más pequeñas y el número de particiones se acerca al infinito.

Entonces, tomamos el límite en ambos lados de ( 2' ). Esto nos da $${\displaystyle \lim _{\|\Delta x_{i}\|\to 0}F(b)-F(a)=\lim _{\|\Delta x_{i}\|\to 0}\sum _{i=1}^{n}[f(c_{i})(\Delta x_{i})].}$$

Ni F ( b ) ni F ( a ) dependen de , por lo que el límite en el lado izquierdo sigue siendo F ( b ) − F ( a ) . ${\displaystyle \|\Delta x_{i}\|}$ $${\displaystyle F(b)-F(a)=\lim _{\|\Delta x_{i}\|\to 0}\sum _{i=1}^{n}[f(c_{i})(\Delta x_{i})].}$$

La expresión del lado derecho de la ecuación define la integral sobre f de a a b . Por lo tanto, obtenemos lo que completa la prueba. $${\displaystyle F(b)-F(a)=\int _{a}^{b}f(x)\,dx,}$$

Relación entre las partes

Como se ha comentado anteriormente, de la primera parte se desprende una versión ligeramente más débil de la segunda parte.

De manera similar, casi parece que la primera parte del teorema se sigue directamente de la segunda. Es decir, supongamos que G es una antiderivada de f . Entonces por el segundo teorema, . Ahora, supongamos que . Entonces F tiene la misma derivada que G , y por lo tanto F ′ = f . Sin embargo, este argumento solo funciona si ya sabemos que f tiene una antiderivada, y la única forma en que sabemos que todas las funciones continuas tienen antiderivadas es por la primera parte del Teorema Fundamental. ^[9] Por ejemplo, si f ( x ) = e ^{− x 2} , entonces f tiene una antiderivada, a saber y no hay una expresión más simple para esta función. Por lo tanto, es importante no interpretar la segunda parte del teorema como la definición de la integral. De hecho, hay muchas funciones que son integrables pero carecen de antiderivadas elementales , y las funciones discontinuas pueden ser integrables pero carecer de antiderivadas en absoluto. Por el contrario, muchas funciones que tienen antiderivadas no son integrables en Riemann (véase la función de Volterra ). ${\textstyle G(x)-G(a)=\int _{a}^{x}f(t)\,dt}$ ${\textstyle F(x)=\int _{a}^{x}f(t)\,dt=G(x)-G(a)}$ $${\displaystyle G(x)=\int _{0}^{x}f(t)\,dt}$$

Ejemplos

Calcular una integral particular

Supongamos que se desea calcular lo siguiente: $${\displaystyle \int _{2}^{5}x^{2}\,dx.}$$

Aquí podemos utilizar y como antiderivada. Por lo tanto: ${\displaystyle f(x)=x^{2}}$ ${\textstyle F(x)={\frac {1}{3}}x^{3}}$ $${\displaystyle \int _{2}^{5}x^{2}\,dx=F(5)-F(2)={\frac {5^{3}}{3}}-{\frac {2^{3}}{3}}={\frac {125}{3}}-{\frac {8}{3}}={\frac {117}{3}}=39.}$$

Usando la primera parte

Supongamos que se debe calcular. Utilizando la primera parte del teorema con se obtiene $${\displaystyle {\frac {d}{dx}}\int _{0}^{x}t^{3}\,dt}$$ ${\displaystyle f(t)=t^{3}}$ $${\displaystyle {\frac {d}{dx}}\int _{0}^{x}t^{3}\,dt=f(x)=x^{3}.}$$

Esto también se puede comprobar utilizando la segunda parte del teorema. En concreto, es una antiderivada de , por lo que ${\textstyle F(t)={\frac {1}{4}}t^{4}}$ ${\displaystyle f(t)}$ $${\displaystyle {\frac {d}{dx}}\int _{0}^{x}t^{3}\,dt={\frac {d}{dx}}F(x)-{\frac {d}{dx}}F(0)={\frac {d}{dx}}{\frac {x^{4}}{4}}=x^{3}.}$$

Una integral donde el corolario es insuficiente

Supongamos que Entonces no es continua en cero. Además, no se trata solo de una cuestión de cómo se define en cero, ya que el límite como de no existe. Por lo tanto, el corolario no se puede utilizar para calcular Pero considere la función Observe que es continua en (incluso en cero por el teorema del apretón ), y es diferenciable en con Por lo tanto, se aplica la segunda parte del teorema, y $${\displaystyle f(x)={\begin{cases}\sin \left({\frac {1}{x}}\right)-{\frac {1}{x}}\cos \left({\frac {1}{x}}\right)&x\neq 0\\0&x=0\\\end{cases}}}$$ ${\displaystyle f(x)}$ ${\displaystyle f}$ ${\displaystyle x\to 0}$ ${\displaystyle f(x)}$ $${\displaystyle \int _{0}^{1}f(x)\,dx.}$$ $${\displaystyle F(x)={\begin{cases}x\sin \left({\frac {1}{x}}\right)&x\neq 0\\0&x=0.\\\end{cases}}}$$ ${\displaystyle F(x)}$ ${\displaystyle [0,1]}$ ${\displaystyle F(x)}$ ${\displaystyle (0,1)}$ ${\displaystyle F'(x)=f(x).}$ $${\displaystyle \int _{0}^{1}f(x)\,dx=F(1)-F(0)=\sin(1).}$$

Ejemplo teórico

El teorema se puede utilizar para demostrar que $${\displaystyle \int _{a}^{b}f(x)dx=\int _{a}^{c}f(x)dx+\int _{c}^{b}f(x)dx.}$$

Puesto que el resultado se sigue de, $${\displaystyle {\begin{aligned}\int _{a}^{b}f(x)dx&=F(b)-F(a),\\\int _{a}^{c}f(x)dx&=F(c)-F(a),{\text{ and }}\\\int _{c}^{b}f(x)dx&=F(b)-F(c),\end{aligned}}}$$ $${\displaystyle F(b)-F(a)=F(c)-F(a)+F(b)-F(c).}$$

Generalizaciones

La función f no tiene por qué ser continua en todo el intervalo. La parte I del teorema dice entonces: si f es cualquier función integrable de Lebesgue en [ a , b ] y x ₀ es un número en [ a , b ] tal que f es continua en x ₀ , entonces $${\displaystyle F(x)=\int _{a}^{x}f(t)\,dt}$$

es diferenciable para x = x ₀ con F ′( x ₀ ) = f ( x ₀ ) . Podemos relajar aún más las condiciones sobre f y suponer que es meramente integrable localmente. En ese caso, podemos concluir que la función F es diferenciable casi en todas partes y F ′( x ) = f ( x ) casi en todas partes. En la línea real, esta afirmación es equivalente al teorema de diferenciación de Lebesgue . Estos resultados siguen siendo válidos para la integral de Henstock-Kurzweil , que permite una clase más amplia de funciones integrables. ^[10]

En dimensiones superiores, el teorema de diferenciación de Lebesgue generaliza el teorema fundamental del cálculo al afirmar que para casi cada x , el valor promedio de una función f sobre una bola de radio r centrada en x tiende a f ( x ) cuando r tiende a 0.

La segunda parte del teorema es válida para cualquier función integrable de Lebesgue f , que tenga una antiderivada F (no todas las funciones integrables la tienen, sin embargo). En otras palabras, si una función real F en [ a , b ] admite una derivada f ( x ) en cada punto x de [ a , b ] y si esta derivada f es integrable de Lebesgue en [ a , b ] , entonces ^[11] $${\displaystyle F(b)-F(a)=\int _{a}^{b}f(t)\,dt.}$$

Este resultado puede fallar para funciones continuas F que admiten una derivada f ( x ) en casi todo punto x , como lo muestra el ejemplo de la función de Cantor . Sin embargo, si F es absolutamente continua , admite una derivada F′ ( x ) en casi todo punto x , y además F′ es integrable, con F ( b ) − F ( a ) igual a la integral de F′ en [ a , b ] . Por el contrario, si f es cualquier función integrable, entonces F como se da en la primera fórmula será absolutamente continua con F′ = f casi en todas partes.

Las condiciones de este teorema pueden ser nuevamente relajadas al considerar las integrales involucradas como integrales de Henstock-Kurzweil . Específicamente, si una función continua F ( x ) admite una derivada f ( x ) en todos los puntos excepto en un número contable, entonces f ( x ) es integrable según Henstock-Kurzweil y F ( b ) − F ( a ) es igual a la integral de f en [ a , b ] . La diferencia aquí es que no es necesario suponer la integrabilidad de f . ^[12]

La versión del teorema de Taylor que expresa el término de error como una integral puede verse como una generalización del teorema fundamental.

Existe una versión del teorema para funciones complejas : supongamos que U es un conjunto abierto en C y f  : U → C es una función que tiene una antiderivada holomorfa F en U . Entonces, para cada curva γ : [ a , b ] → U , la integral de la curva se puede calcular como $${\displaystyle \int _{\gamma }f(z)\,dz=F(\gamma (b))-F(\gamma (a)).}$$

El teorema fundamental puede generalizarse a integrales de curvas y superficies en dimensiones superiores y en variedades . Una de esas generalizaciones que ofrece el cálculo de superficies en movimiento es la evolución temporal de las integrales . Las extensiones más conocidas del teorema fundamental del cálculo en dimensiones superiores son el teorema de la divergencia y el teorema del gradiente .

Una de las generalizaciones más poderosas en esta dirección es el teorema generalizado de Stokes (a veces conocido como el teorema fundamental del cálculo multivariable): ^[13] Sea M una variedad suave orientada por partes de dimensión n y sea una forma ( n  − 1) suave y compactamente soportada en M . Si ∂ M denota el límite de M dada su orientación inducida , entonces ${\displaystyle \omega }$ $${\displaystyle \int _{M}d\omega =\int _{\partial M}\omega .}$$

Aquí d es la derivada exterior , que se define utilizando únicamente la estructura de la variedad.

El teorema se utiliza a menudo en situaciones en las que M es una subvariedad orientada e incorporada de alguna variedad mayor (por ejemplo, R ^k ) en la que se define la forma . ${\displaystyle \omega }$

El teorema fundamental del cálculo nos permite plantear una integral definida como una ecuación diferencial ordinaria de primer orden. puede plantearse como con como el valor de la integral. $${\displaystyle \int _{a}^{b}f(x)\,dx}$$ $${\displaystyle {\frac {dy}{dx}}=f(x),\;\;y(a)=0}$$ ${\displaystyle y(b)}$

Véase también

• Portal de matemáticas

• Diferenciación bajo el signo integral
• Serie telescópica
• Teorema fundamental del cálculo para integrales de línea
• Notación para diferenciación

Notas

Referencias

1. Weisstein, Eric W. "Primer teorema fundamental del cálculo". mathworld.wolfram.com . Consultado el 15 de abril de 2024 .
2. Malet, Antoni (1993). «James Gregorie sobre las tangentes y la regla de «Taylor» para desarrollos de series». Archivo de Historia de las Ciencias Exactas . 46 (2). Springer-Verlag : 97–137. doi :10.1007/BF00375656. S2CID  120101519. El pensamiento de Gregorie, por otra parte, pertenece a un marco conceptual de marcado carácter geométrico. (página 137)
3. Véase, por ejemplo, Marlow Anderson, Victor J. Katz, Robin J. Wilson, Sherlock Holmes en Babilonia y otros cuentos de historia matemática , Mathematical Association of America, 2004, pág. 114.
4. Gregorio, James (1668). Geometriae Pars Universalis. Museo Galileo : Patavii: typis heredum Pauli Frambotti.
5. Niño, James Mark; Barrow, Isaac (1916). Las lecciones geométricas de Isaac Barrow. Chicago: Open Court Publishing Company .
6. Apóstol 1967, §5.1
7. Apóstol 1967, §5.3
8. Leithold, L. (1996), El cálculo de una sola variable (6.ª ed.), Nueva York: HarperCollins College Publishers, pág. 380.
9. Spivak, Michael (1980), Cálculo (2.ª ed.), Houston, Texas: Publish or Perish Inc.
10. Bartle (2001), Teoría 4.11.
11. Rudin 1987, tomo 7.21
12. Bartle (2001), Teoría 4.7.
13. Spivak, M. (1965). Cálculo de variedades . Nueva York: WA Benjamin. pp. 124-125. ISBN. 978-0-8053-9021-6.

Bibliografía

• Apostol, Tom M. (1967), Cálculo, vol. 1: Cálculo de una variable con una introducción al álgebra lineal (2.ª ed.), Nueva York: John Wiley & Sons , ISBN 978-0-471-00005-1.
• Bartle, Robert (2001), Una teoría moderna de la integración , AMS, ISBN 0-8218-0845-1.
• Leithold, L. (1996), El cálculo de una sola variable (6.ª ed.), Nueva York: HarperCollins College Publishers.
• Rudin, Walter (1987), Análisis real y complejo (tercera edición), Nueva York: McGraw-Hill Book Co., ISBN 0-07-054234-1

Lectura adicional

• Courant, Richard; John, Fritz (1965), Introducción al cálculo y al análisis , Springer.
• Larson, Ron; Edwards, Bruce H.; Heyd, David E. (2002), Cálculo de una sola variable (7.ª ed.), Boston: Houghton Mifflin Company, ISBN 978-0-618-14916-2.
• Malet, A. , Estudios sobre James Gregorie (1638-1675) (Tesis doctoral, Princeton, 1989).
• Hernández Rodríguez, OA; López Fernández, JM. "La enseñanza del teorema fundamental del cálculo: una reflexión histórica", Loci: Convergencia ( MAA ), enero de 2012.
• Stewart, J. (2003), "Teorema fundamental del cálculo", Cálculo: trascendentales tempranos , Belmont, California: Thomson/Brooks/Cole.
• Turnbull, HW, ed. (1939), Volumen conmemorativo del tricentenario de James Gregory , Londres{{citation}}: CS1 maint: location missing publisher (link).

Enlaces externos

• "Teorema fundamental del cálculo", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Prueba euclidiana del teorema fundamental del cálculo en la convergencia de James Gregory
• Demostración del teorema fundamental del cálculo de Isaac Barrow
• Teorema fundamental del cálculo en imomath.com
• Prueba alternativa del teorema fundamental del cálculo
• Teorema fundamental del cálculo MIT .
• Teorema fundamental del cálculo Mathworld .