La distancia instantánea Tierra-Luna , o distancia a la Luna , es la distancia desde el centro de la Tierra hasta el centro de la Luna . La distancia lunar ( LD o ), o distancia característica Tierra-Luna , es una unidad de medida en astronomía . Más técnicamente, es el semieje mayor de la órbita lunar geocéntrica . La distancia lunar es en promedio de aproximadamente 385.000 km (239.000 mi), o 1,28 segundos luz ; esto es aproximadamente 30 veces el diámetro de la Tierra o 9,5 veces la circunferencia de la Tierra . Alrededor de 389 distancias lunares conforman una unidad astronómica UA (aproximadamente la distancia de la Tierra al Sol).
La distancia lunar se utiliza comúnmente para expresar la distancia a los encuentros de objetos cercanos a la Tierra . [1] El semieje mayor lunar es un dato astronómico importante; la precisión de pocos milímetros de las mediciones de rango determina el semieje mayor a unos pocos decímetros; tiene implicaciones para probar teorías gravitacionales como la relatividad general , [2] y para refinar otros valores astronómicos, como la masa , [3] el radio , [4] y la rotación de la Tierra. [5] La medición también es útil para caracterizar el radio lunar , así como la masa y la distancia al Sol .
Las mediciones de precisión milimétrica de la distancia lunar se realizan midiendo el tiempo que tarda el haz de luz láser en viajar entre las estaciones en la Tierra y los retrorreflectores colocados en la Luna. La Luna se aleja de la Tierra en espiral a una velocidad media de 3,8 cm (1,5 pulgadas) por año, según lo detectado por el experimento Lunar Laser Ranging . [6] [7] [8]

Debido a la influencia del Sol y otras perturbaciones, la Luna no se mueve en una elipse verdadera alrededor de la Tierra. No obstante, se han utilizado diferentes métodos para definir un semieje mayor . Ernest William Brown proporcionó una fórmula para la paralaje de la Luna vista desde lados opuestos de la Tierra, que involucra términos trigonométricos . Esto es equivalente a una fórmula para la inversa de la distancia, y el valor promedio de esta es el inverso de 384.399 km (238.854 mi). [9] [10] Por otro lado, la distancia promediada en el tiempo (en lugar de la inversa de la distancia inversa promedio) entre los centros de la Tierra y la Luna es de 385.000,6 km (239.228,3 mi). También se puede modelar la órbita como una elipse que cambia constantemente, y en este caso se puede encontrar una fórmula para el semieje mayor, que nuevamente involucra términos trigonométricos. El valor promedio por este método es de 383.397 km. [11]
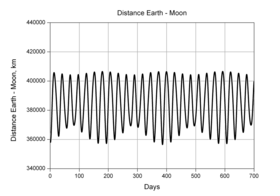
La distancia real varía a lo largo de la órbita de la Luna . Los valores en el punto de máxima aproximación ( perigeo ) o en el punto de máxima lejanía ( apogeo ) son tanto más raros cuanto más extremos son. El gráfico de la derecha muestra la distribución del perigeo y el apogeo a lo largo de seis mil años.
Jean Meeus da los siguientes valores extremos para el período 1500 a. C. al 8000 d. C.: [12]

La distancia lunar instantánea cambia constantemente. La distancia real entre la Luna y la Tierra puede cambiar tan rápido como75 metros por segundo , [20] o más de 1.000 km (620 mi) en sólo 6 horas, debido a su órbita no circular. [21] Hay otros efectos que también influyen en la distancia lunar. Algunos factores incluyen:

La fórmula de Chapront y Touzé para la distancia en kilómetros comienza con los términos: [9]
donde es la anomalía media (más o menos cuánto se ha movido la luna desde el perigeo) y es la elongación media (más o menos cuánto se ha movido desde la conjunción con el Sol en la luna nueva). Se pueden calcular a partir de
GM = 134,963 411 38° + 13,064 992 953 630°/d · t
D = 297,850 204 20° + 12,190 749 117 502°/d · t
donde t es el tiempo (en días) desde el 1 de enero de 2000 (ver Época (astronomía) ). Esto muestra que el perigeo más pequeño ocurre en luna nueva o luna llena (ca 356870 km), al igual que el apogeo más grande (ca 406079 km), mientras que el perigeo más grande será alrededor de la media luna (ca 370180 km), al igual que el apogeo más pequeño (ca 404593 km). Los valores exactos serán ligeramente diferentes debido a otros términos. Dos veces en cada ciclo de luna llena de aproximadamente 411 días habrá un perigeo mínimo y un apogeo máximo, separados por dos semanas, y un perigeo máximo y un apogeo mínimo, también separados por dos semanas.
La distancia a la Luna se puede medir con una precisión de2 mm durante un período de muestreo de 1 hora, [22] lo que da como resultado una incertidumbre general de un decímetro para el semieje mayor. Sin embargo, debido a su órbita elíptica con excentricidad variable, la distancia instantánea varía con la periodicidad mensual. Además, la distancia se ve perturbada por los efectos gravitacionales de varios cuerpos astronómicos, el más significativo es el Sol y, en menor medida, Venus y Júpiter. Otras fuerzas responsables de pequeñas perturbaciones son: la atracción gravitacional hacia otros planetas del Sistema Solar y hacia asteroides; las fuerzas de marea; y los efectos relativistas. [23] [24] El efecto de la presión de radiación del Sol contribuye con una cantidad de ±3,6 mm a la distancia lunar. [22]
Aunque la incertidumbre instantánea es de unos pocos milímetros, la distancia lunar medida puede variar en más de 30.000 km (19.000 mi) con respecto al valor medio a lo largo de un mes típico. Estas perturbaciones se comprenden bien [25] y la distancia lunar se puede modelar con precisión a lo largo de miles de años. [23]

A través de la acción de las fuerzas de marea , el momento angular de la rotación de la Tierra se transfiere lentamente a la órbita de la Luna. [26] El resultado es que la velocidad de giro de la Tierra está disminuyendo gradualmente (a una tasa de2,4 milisegundos/siglo ), [27] [28] [29] [30] y la órbita lunar se está expandiendo gradualmente. La tasa de recesión es3,830 ± 0,008 cm por año . [25] [28] Sin embargo, se cree que esta tasa ha aumentado recientemente, como una tasa de3,8 cm/año implicaría que la Luna tiene sólo 1.500 millones de años, mientras que el consenso científico apoya una edad de unos 4.000 millones de años. [31] También se cree que esta tasa de recesión anómalamente alta puede seguir acelerándose. [32]
En teoría, la distancia lunar seguirá aumentando hasta que la Tierra y la Luna queden atrapadas por las mareas , como ocurre con Plutón y Caronte . Esto ocurriría cuando la duración del período orbital lunar sea igual al período de rotación de la Tierra, que se estima en 47 días terrestres. Los dos cuerpos estarían entonces en equilibrio y no se intercambiaría más energía rotacional. Sin embargo, los modelos predicen que se necesitarían 50 mil millones de años para alcanzar esta configuración, [33] que es significativamente más larga que la vida útil esperada del Sistema Solar .
Las mediciones láser muestran que la distancia lunar promedio está aumentando, lo que implica que la Luna estaba más cerca en el pasado y que los días de la Tierra eran más cortos. Los estudios fósiles de conchas de moluscos de la era Campaniana (hace 80 millones de años) muestran que hubo 372 días (de 23 h 33 min) por año durante ese tiempo, lo que implica que la distancia lunar era de aproximadamente 60,05 R 🜨 (383 000 km o 238 000 mi). [26] Existe evidencia geológica de que la distancia lunar promedio fue de aproximadamente 52 R 🜨 (332 000 km o 205 000 mi) durante la Era Precámbrica ; 2500 millones de años AP . [31]
La hipótesis del impacto gigante, ampliamente aceptada, afirma que la Luna se creó como resultado de un impacto catastrófico entre la Tierra y otro planeta, lo que dio lugar a una reacumulación de fragmentos a una distancia inicial de 3,8 R 🜨 (24 000 km o 15 000 mi). [34] Esta teoría supone que el impacto inicial ocurrió hace 4500 millones de años. [35]
Hasta finales de la década de 1950, todas las mediciones de la distancia lunar se basaban en mediciones angulares ópticas: la primera medición precisa fue la de Hiparco en el siglo II a. C. La era espacial marcó un punto de inflexión en el que la precisión de este valor mejoró mucho. Durante las décadas de 1950 y 1960, se realizaron experimentos con radar, láser y naves espaciales, que se llevaron a cabo con la ayuda del procesamiento y modelado informáticos. [36]
Algunos métodos históricamente significativos o interesantes para determinar la distancia lunar:
El método más antiguo para determinar la distancia lunar implicaba medir el ángulo entre la Luna y un punto de referencia elegido desde varias ubicaciones, simultáneamente. La sincronización se puede coordinar haciendo mediciones en un momento predeterminado o durante un evento que sea observable para todas las partes. Antes de los cronómetros mecánicos precisos, el evento de sincronización era típicamente un eclipse lunar o el momento en que la Luna cruzaba el meridiano (si los observadores compartían la misma longitud). Esta técnica de medición se conoce como paralaje lunar .
Para una mayor precisión, el ángulo medido se puede ajustar para tener en cuenta la refracción y la distorsión de la luz que pasa a través de la atmósfera.
Los primeros intentos de medir la distancia a la Luna se basaron en observaciones de eclipses lunares combinadas con el conocimiento del radio de la Tierra y la comprensión de que el Sol está mucho más lejos que la Luna. Al observar la geometría de un eclipse lunar, la distancia lunar se puede calcular mediante trigonometría .
Los primeros relatos de intentos de medir la distancia lunar utilizando esta técnica fueron realizados por el astrónomo y matemático griego Aristarco de Samos en el siglo IV a. C. [37] y más tarde por Hiparco , cuyos cálculos produjeron un resultado de 59-67 R 🜨 (376 000 –427 000 km o233 000 –265 000 mi ). [38] Este método más tarde se utilizó en el trabajo de Ptolomeo , [39] quien produjo un resultado de 64+1 ⁄ 6 R 🜨 (409 000 km o253 000 mi ) en su punto más lejano. [40]
Una expedición del astrónomo francés ACD Crommelin observó tránsitos meridianos lunares en la misma noche desde dos lugares diferentes. Mediciones cuidadosas realizadas entre 1905 y 1910 midieron el ángulo de elevación en el momento en que un cráter lunar específico ( Mösting A ) cruzó el meridiano local, desde estaciones en Greenwich y en el Cabo de Buena Esperanza . [41] Se calculó una distancia con una incertidumbre de30 km , y este siguió siendo el valor definitivo de la distancia lunar durante el siguiente medio siglo.
Al registrar el instante en que la Luna oculta una estrella de fondo (o de manera similar, midiendo el ángulo entre la Luna y una estrella de fondo en un momento predeterminado), se puede determinar la distancia lunar, siempre que las mediciones se tomen desde múltiples ubicaciones con una separación conocida.
Los astrónomos O'Keefe y Anderson calcularon la distancia lunar observando cuatro ocultaciones desde nueve lugares en 1952. [42] Calcularon un semieje mayor de384 407,6 ± 4,7 km (238 859,8 ± 2,9 mi). Este valor fue refinado en 1962 por Irene Fischer , quien incorporó datos geodésicos actualizados para producir un valor de384.403,7 ± 2 km ( 238.857,4 ± 1 mi). [4]

La distancia a la Luna se midió por primera vez mediante radar en 1946 como parte del Proyecto Diana . [44]
Más tarde, en 1957, se llevó a cabo un experimento en el Laboratorio de Investigación Naval de Estados Unidos que utilizó el eco de las señales de radar para determinar la distancia entre la Tierra y la Luna. Los pulsos de radar duranSe transmitieron 2 μs desde una antena parabólica de 15 m de diámetro. Después de que las ondas de radio hicieran eco en la superficie de la Luna, se detectó la señal de retorno y se midió el tiempo de retardo. A partir de esa medición, se pudo calcular la distancia. Sin embargo, en la práctica, la relación señal-ruido era tan baja que no se podía producir una medición precisa de manera confiable. [45]
El experimento se repitió en 1958 en el Royal Radar Establishment , en Inglaterra. Los pulsos de radar duranSe transmitieron 5 μs con una potencia pico de 2 megavatios, a una frecuencia de repetición de 260 pulsos por segundo. Después de que las ondas de radio hicieran eco en la superficie de la Luna, se detectó la señal de retorno y se midió el tiempo de retardo. Se sumaron varias señales para obtener una señal confiable superponiendo trazas del osciloscopio sobre una película fotográfica. A partir de las mediciones, se calculó la distancia con una incertidumbre de 1,25 km (0,777 mi). [46]
Estos experimentos iniciales tenían como objetivo ser experimentos de prueba de concepto y solo duraron un día. Los experimentos posteriores, que duraron un mes, produjeron un semieje mayor de384 402 ± 1,2 km (238 856 ± 0,75 mi), [47] que era la medición más precisa de la distancia lunar en ese momento.

En 1962, un equipo del Instituto Tecnológico de Massachusetts y un equipo soviético del Observatorio Astrofísico de Crimea realizaron un experimento que midió el tiempo de ida y vuelta de los pulsos láser reflejados directamente desde la superficie de la Luna . [48]
Durante las misiones Apolo en 1969, los astronautas colocaron retrorreflectores en la superficie de la Luna con el fin de perfeccionar la exactitud y precisión de esta técnica. Las mediciones están en curso e involucran múltiples instalaciones láser. La precisión instantánea de los experimentos de medición de distancias por láser lunar puede lograr una pequeña resolución milimétrica y es el método más confiable para determinar la distancia lunar. Se determinó que el semieje mayor es de 384.399,0 km. [10]
Gracias a la accesibilidad moderna de dispositivos de cronometraje precisos, cámaras digitales de alta resolución, receptores GPS , computadoras potentes y comunicación casi instantánea, es posible que los astrónomos aficionados realicen mediciones de alta precisión de la distancia lunar.
El 23 de mayo de 2007 se tomaron fotografías digitales de la Luna durante una ocultación casi total de Regulus desde dos lugares, en Grecia e Inglaterra. Midiendo la paralaje entre la Luna y la estrella de fondo elegida, se calculó la distancia lunar. [49]
Un proyecto más ambicioso llamado "Campaña Aristarco" se llevó a cabo durante el eclipse lunar del 15 de abril de 2014. [21] Durante este evento, se invitó a los participantes a registrar una serie de cinco fotografías digitales desde la salida de la luna hasta su culminación (el punto de mayor altitud).
El método aprovechó el hecho de que la Luna está realmente más cerca de un observador cuando está en su punto más alto en el cielo, en comparación con cuando está en el horizonte. Aunque parece que la Luna es más grande cuando está cerca del horizonte, lo cierto es lo contrario. Este fenómeno se conoce como la ilusión lunar . La razón de la diferencia de distancia es que la distancia desde el centro de la Luna al centro de la Tierra es casi constante durante toda la noche, pero un observador en la superficie de la Tierra está en realidad a 1 radio terrestre del centro de la Tierra. Este desfase lo lleva más cerca de la Luna cuando está en lo alto.
Las cámaras modernas han logrado una resolución capaz de captar la Luna con suficiente precisión para detectar y medir esta pequeña variación en el tamaño aparente. Los resultados de este experimento se calcularon como LD =60,51+3,91
-4,19 R 🜨 . El valor aceptado para esa noche fue 60,61 R 🜨 , lo que implica una precisión del 3%. La ventaja de este método es que el único equipo de medición necesario es una cámara digital moderna (equipada con un reloj preciso y un receptor GPS).
Otros métodos experimentales para medir la distancia lunar que pueden realizar los astrónomos aficionados incluyen:
{{cite journal}}: CS1 maint: varios nombres: lista de autores ( enlace )