Efecto piel

Tendencia del flujo de corriente alterna en la capa exterior de un conductor

Distribución del flujo de corriente en un conductor cilíndrico, mostrado en sección transversal. Para corriente alterna , la densidad de corriente disminuye exponencialmente desde la superficie hacia el interior. La profundidad superficial, δ, se define como la profundidad donde la densidad de corriente es solo 1/e (aproximadamente el 37 %) del valor en la superficie; depende de la frecuencia de la corriente y de las propiedades eléctricas y magnéticas del conductor.

Las cocinas de inducción utilizan bobinas trenzadas ( alambre Litz ) para reducir el calentamiento de la propia bobina debido al efecto pelicular. Las frecuencias de CA que se utilizan en las cocinas de inducción son mucho más altas que la frecuencia de la red eléctrica estándar, normalmente alrededor de 25–50 kHz.

En electromagnetismo , el efecto pelicular es la tendencia de una corriente eléctrica alterna (CA) a distribuirse dentro de un conductor de tal manera que la densidad de corriente es mayor cerca de la superficie del conductor y disminuye exponencialmente a mayor profundidad en el conductor. Es causado por corrientes de Foucault opuestas inducidas por el campo magnético cambiante resultante de la corriente alterna. La corriente eléctrica fluye principalmente en la piel del conductor, entre la superficie exterior y un nivel llamado profundidad de la piel .

La profundidad de la piel depende de la frecuencia de la corriente alterna; a medida que aumenta la frecuencia, el flujo de corriente se vuelve más concentrado cerca de la superficie, lo que resulta en una menor profundidad de la piel. El efecto de piel reduce la sección transversal efectiva del conductor y, por lo tanto, aumenta su resistencia efectiva . A 60 Hz en el cobre, la profundidad de piel es de aproximadamente 8,5 mm. A altas frecuencias, la profundidad de piel se vuelve mucho menor.

La mayor resistencia de corriente alterna causada por el efecto pelicular se puede mitigar utilizando un cable multifilar especializado llamado cable litz . Debido a que el interior de un conductor grande transporta poca corriente, se pueden utilizar conductores tubulares para ahorrar peso y costos.

El efecto pelicular tiene consecuencias prácticas en el análisis y diseño de circuitos de radiofrecuencia y microondas , líneas de transmisión (o guías de ondas) y antenas . También es importante en las frecuencias de red (50–60 Hz) en los sistemas de transmisión y distribución de energía eléctrica de CA. Es una de las razones por las que se prefiere la corriente continua de alto voltaje para la transmisión de energía a larga distancia.

El efecto fue descrito por primera vez en un artículo de Horace Lamb en 1883 para el caso de conductores esféricos, ^[1] y fue generalizado a conductores de cualquier forma por Oliver Heaviside en 1885.

Causa

Causa del efecto piel. Una corriente principal I que fluye a través de un conductor induce un campo magnético H . Si la corriente aumenta, como en esta figura, el aumento resultante de H induce corrientes de Foucault circulantes separadas I _W que anulan parcialmente el flujo de corriente en el centro y lo refuerzan cerca de la piel.

Los conductores, normalmente en forma de cables, pueden utilizarse para transferir energía eléctrica o señales utilizando una corriente alterna que fluye a través de ese conductor. Los portadores de carga que constituyen esa corriente, normalmente electrones , son impulsados ​​por un campo eléctrico debido a la fuente de energía eléctrica. Una corriente en un conductor produce un campo magnético dentro y alrededor del conductor. Cuando la intensidad de la corriente en un conductor cambia, el campo magnético también cambia. El cambio en el campo magnético, a su vez, crea un campo eléctrico que se opone al cambio en la intensidad de la corriente. Este campo eléctrico opuesto se llama fuerza contraelectromotriz (FEM posterior). La FEM posterior es más fuerte/más concentrada en el centro del conductor, permitiendo la corriente solo cerca de la capa exterior del conductor, como se muestra en el diagrama de la derecha. ^{[2] [3]}

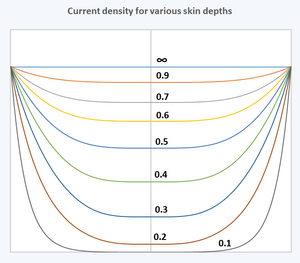
Independientemente de la fuerza impulsora, se ha descubierto que la densidad de corriente es mayor en la superficie del conductor, con una magnitud reducida en las zonas más profundas del conductor. Esa disminución de la densidad de corriente se conoce como efecto pelicular y la profundidad pelicular es una medida de la profundidad a la que la densidad de corriente cae a 1/e de su valor cerca de la superficie. Más del 98% de la corriente fluirá dentro de una capa de 4 veces la profundidad pelicular desde la superficie. Este comportamiento es distinto al de la corriente continua, que normalmente se distribuirá de manera uniforme sobre la sección transversal del cable.

Una corriente alterna también puede inducirse en un conductor debido a un campo magnético alterno de acuerdo con la ley de inducción . Por lo tanto, una onda electromagnética que incide sobre un conductor generalmente producirá dicha corriente; esto explica la atenuación de las ondas electromagnéticas en los metales. Aunque el término efecto pelicular se asocia con mayor frecuencia a aplicaciones que implican la transmisión de corrientes eléctricas, la profundidad pelicular también describe la disminución exponencial de los campos eléctricos y magnéticos, así como la densidad de corrientes inducidas, dentro de un material a granel cuando una onda plana incide sobre él con una incidencia normal .

Fórmula

La densidad de corriente alterna J en un conductor disminuye exponencialmente a partir de su valor en la superficie J _S según la profundidad d desde la superficie, de la siguiente manera: ^{[4] : 362} donde se denomina profundidad pelicular , que se define como la profundidad por debajo de la superficie del conductor en la que la densidad de corriente ha caído a 1/ e (aproximadamente 0,37) de J _S . La parte imaginaria del exponente indica que la fase de la densidad de corriente se retrasa 1 radián por cada profundidad pelicular de penetración. Una longitud de onda completa en el conductor requiere 2 π profundidades peliculares, en cuyo punto la densidad de corriente se atenúa a e ^{−2 π} (1,87×10 ⁻³ , o −54,6 dB) de su valor superficial. La longitud de onda en el conductor es mucho más corta que la longitud de onda en el vacío , o equivalentemente, la velocidad de fase en un conductor es mucho más lenta que la velocidad de la luz en el vacío. Por ejemplo, una onda de radio de 1 MHz tiene una longitud de onda en el vacío λ _o de aproximadamente 300 m, mientras que en el cobre, la longitud de onda se reduce a solo unos 0,5 mm con una velocidad de fase de solo unos 500 m/s. Como consecuencia de la ley de Snell y de esta ínfima velocidad de fase en un conductor, cualquier onda que entre en un conductor, incluso con incidencia rasante, se refracta esencialmente en la dirección perpendicular a la superficie del conductor. $${\displaystyle J=J_{\mathrm {S} }\,e^{-{(1+j)d/\delta }}}$$ ${\displaystyle \delta }$

La fórmula general para la profundidad de la piel cuando no hay pérdida dieléctrica o magnética es: ^{[5] [6]} $${\displaystyle \delta ={\sqrt {{\frac {\,2\rho \,}{\omega \mu }}\left({\sqrt {1+\left({\rho \omega \varepsilon }\right)^{2}\,}}+\rho \omega \varepsilon \right)\,}}}$$

dónde

• ${\displaystyle \rho =}$ resistividad del conductor
• ${\displaystyle \omega =}$ frecuencia angular de la corriente donde es la frecuencia. ${\displaystyle =2\pi f,}$ ${\displaystyle f}$
• ${\displaystyle \mu =}$ permeabilidad del conductor, ${\displaystyle \mu _{r}\,\mu _{0}}$
• ${\displaystyle \mu _{r}=}$permeabilidad magnética relativa del conductor
• ${\displaystyle \mu _{0}=}$la permeabilidad del espacio libre
• ${\displaystyle \varepsilon =}$ permitividad del conductor, ${\displaystyle \varepsilon _{r}\,\varepsilon _{0}}$
• ${\displaystyle \varepsilon _{r}=}$permitividad relativa del conductor
• ${\displaystyle \varepsilon _{0}=}$la permitividad del espacio libre .

En frecuencias muy inferiores, la cantidad dentro del radical grande está cerca de la unidad y la fórmula se da más comúnmente como: ${\displaystyle 1/(\rho \varepsilon )}$ $${\displaystyle \delta ={\sqrt {{\frac {\,2\rho \,}{\omega \mu }}\,}}~.}$$

Esta fórmula es válida en frecuencias alejadas de las fuertes resonancias atómicas o moleculares (donde tendría una gran parte imaginaria) y en frecuencias que están muy por debajo tanto de la frecuencia del plasma del material (que depende de la densidad de electrones libres en el material) como del recíproco del tiempo medio entre colisiones que involucran a los electrones de conducción. En buenos conductores como los metales, todas esas condiciones están aseguradas al menos hasta las frecuencias de microondas, lo que justifica la validez de esta fórmula. ^{[nota 1]} Por ejemplo, en el caso del cobre, esto sería cierto para frecuencias muy por debajo ${\displaystyle \varepsilon }$10 ^18Hz . ​

Sin embargo, en conductores muy malos, a frecuencias suficientemente altas, el factor bajo el radical grande aumenta. A frecuencias mucho más altas, se puede demostrar que la profundidad de la piel, en lugar de seguir disminuyendo, se acerca a un valor asintótico: ${\displaystyle 1/(\rho \varepsilon )}$ $${\displaystyle \delta \approx {2\rho }{\sqrt {{\frac {\,\varepsilon \,}{\mu }}\,}}~.}$$

Esta desviación de la fórmula habitual sólo se aplica a materiales de conductividad relativamente baja y a frecuencias en las que la longitud de onda del vacío no es mucho mayor que la propia profundidad de la piel. Por ejemplo, el silicio en masa (sin dopar) es un mal conductor y tiene una profundidad de piel de unos 40 metros a 100 kHz ( λ = 3 km). Sin embargo, a medida que la frecuencia se incrementa hasta el rango de los megahercios, su profundidad de piel nunca cae por debajo del valor asintótico de 11 metros. La conclusión es que en malos conductores sólidos, como el silicio sin dopar, el efecto pelicular no necesita tenerse en cuenta en la mayoría de las situaciones prácticas: cualquier corriente se distribuye de manera uniforme a lo largo de la sección transversal del material, independientemente de su frecuencia.

Alambre redondo

Cuando la profundidad de la piel no es pequeña con respecto al radio del cable, la densidad de corriente se puede describir en términos de funciones de Bessel . La densidad de corriente dentro del cable redondo, lejos de las influencias de otros campos, como función de la distancia desde el eje, se da por: ^{[7] : 38}

Densidad de corriente en un cable redondo para distintas profundidades de la piel. Los números que se muestran en cada curva son la relación entre la profundidad de la piel y el radio del cable. La curva que se muestra con el signo de infinito es el caso de frecuencia cero (CC). Todas las curvas están normalizadas de modo que la densidad de corriente en la superficie sea la misma. El eje horizontal es la posición dentro del cable y los extremos izquierdo y derecho son la superficie del cable. El eje vertical es la densidad de corriente relativa.

$${\displaystyle \mathbf {J} (r)={\frac {k\mathbf {I} }{2\pi R}}{\frac {J_{0}(kr)}{J_{1}(kR)}}=\mathbf {J} (R){\frac {J_{0}(kr)}{J_{0}(kR)}}}$$

dónde

• ${\displaystyle r={}}$distancia desde el eje del alambre
• ${\displaystyle R={}}$radio del alambre
• ${\displaystyle \mathbf {J} (r)={}}$fasor de densidad de corriente a una distancia, r , del eje del cable
• ${\displaystyle \mathbf {J} (R)={}}$Fasor de densidad de corriente en la superficie del cable.
• ${\displaystyle \mathbf {I} =}$fasor de corriente total
• ${\displaystyle J_{0}={}}$Función de Bessel de primer tipo, orden 0
• ${\displaystyle J_{1}={}}$Función de Bessel de primer tipo, orden 1
• ${\displaystyle k={\sqrt {\frac {-j\omega \mu }{\rho }}}={\frac {1-j}{\delta }}}$El número de onda en el conductor
• ${\displaystyle \delta ={\sqrt {\frac {2\rho }{\omega \mu }}}}$También llamado profundidad de la piel.
• ${\displaystyle \rho ={}}$resistividad del conductor
• ${\displaystyle \mu _{r}={}}$permeabilidad magnética relativa del conductor
• ${\displaystyle \mu =\mu _{r}\mu _{0}}$

Como es compleja, las funciones de Bessel también lo son. La amplitud y la fase de la densidad de corriente varían con la profundidad. ${\displaystyle k}$

Derivación

Combinando la ecuación de onda electromagnética y la ley de Ohm se obtiene La solución de esta ecuación es, para una corriente finita en el centro del conductor, donde es una función de Bessel de primer orden y es un fasor constante. Para satisfacer la condición de contorno para la densidad de corriente en la superficie del conductor, debe ser Por lo tanto, $${\displaystyle \nabla ^{2}\mathbf {J} (r)+k^{2}\mathbf {J} (r)={\frac {\partial ^{2}}{\partial r^{2}}}\mathbf {J} (r)+{\frac {1}{r}}{\frac {\partial }{\partial r}}\mathbf {J} (r)+k^{2}\mathbf {J} (r)=0.}$$ $${\displaystyle \mathbf {J} (r)=\mathbf {C} J_{0}(kr),}$$ ${\displaystyle J_{0}}$ ${\displaystyle 0}$ ${\displaystyle \mathbf {C} }$ ${\displaystyle \mathbf {J} (R),}$ ${\displaystyle \mathbf {C} }$ ${\displaystyle {\frac {\mathbf {J} (R)}{J_{0}(kR)}}.}$ $${\displaystyle \mathbf {J} (r)=\mathbf {J} (R){\frac {J_{0}(kr)}{J_{0}(kR)}}.}$$

Impedancia

Resistencia

El efecto más importante del efecto pelicular sobre la impedancia de un solo cable es el aumento de la resistencia del cable y las pérdidas consecuentes . La resistencia efectiva debida a una corriente confinada cerca de la superficie de un conductor grande (mucho más grueso que δ ) se puede resolver como si la corriente fluyera uniformemente a través de una capa de espesor δ en función de la resistividad de CC de ese material. El área de sección transversal efectiva es aproximadamente igual a δ multiplicada por la circunferencia del conductor. Por lo tanto, un conductor cilíndrico largo, como un cable, que tiene un diámetro D grande en comparación con δ , tiene una resistencia aproximadamente igual a la de un tubo hueco con espesor de pared δ que transporta corriente continua. La resistencia de CA de un cable de longitud ℓ y resistividad es: ${\displaystyle \rho }$ $${\displaystyle R\approx {{\ell \rho } \over {\pi (D-\delta )\delta }}\approx {{\ell \rho } \over {\pi D\delta }}}$$

La aproximación final anterior supone . ${\displaystyle D\gg \delta }$

Una fórmula conveniente (atribuida a FE Terman ) para el diámetro D _W de un cable de sección transversal circular cuya resistencia aumentará en un 10% a la frecuencia f es: ^[8] $${\displaystyle D_{\mathrm {W} }={\frac {200~\mathrm {mm} }{\sqrt {f/\mathrm {Hz} }}}}$$

Esta fórmula para el aumento de la resistencia de CA es precisa solo para un cable aislado. Para cables cercanos, por ejemplo, en un cable o una bobina, la resistencia de CA también se ve afectada por el efecto de proximidad , que puede causar un aumento adicional en la resistencia de CA. La impedancia interna por unidad de longitud de un segmento de cable redondo está dada por: ^{[7] : 40} $${\displaystyle \mathbf {Z} _{\text{int}}={\frac {k\rho }{2\pi R}}{\frac {J_{0}(kR)}{J_{1}(kR)}}.}$$

Esta impedancia es una cantidad compleja que corresponde a una resistencia (real) en serie con la reactancia (imaginaria) debida a la autoinducción interna del cable , por unidad de longitud.

Inductancia

Una parte de la inductancia de un cable se puede atribuir al campo magnético dentro del propio cable, que se denomina inductancia interna ; esto explica la reactancia inductiva (parte imaginaria de la impedancia) dada por la fórmula anterior. En la mayoría de los casos, se trata de una pequeña parte de la inductancia de un cable que incluye el efecto de la inducción de los campos magnéticos fuera del cable producidos por la corriente en el cable. A diferencia de la inductancia externa , la inductancia interna se reduce por el efecto pelicular, es decir, en frecuencias donde la profundidad pelicular ya no es grande en comparación con el tamaño del conductor. ^[9] Este pequeño componente de la inductancia se acerca a un valor de (50 nH/m para cables no magnéticos) a bajas frecuencias, independientemente del radio del cable. Su reducción con el aumento de la frecuencia, a medida que la relación entre la profundidad pelicular y el radio del cable cae por debajo de aproximadamente 1, se representa en el gráfico adjunto y explica la reducción de la inductancia del cable telefónico con el aumento de la frecuencia en la tabla siguiente. ${\displaystyle {\frac {\mu }{8\pi }}}$

El componente interno de la inductancia de un cable redondo en relación con la relación entre la profundidad de la piel y el radio. Ese componente de la autoinductancia se reduce por debajo de μ /8 π a medida que la profundidad de la piel se hace pequeña (a medida que aumenta la frecuencia).

Relación entre la resistencia de CA y la resistencia de CC de un cable redondo y la relación entre el radio del cable y la profundidad de la piel. A medida que la profundidad de la piel se hace pequeña en relación con el radio, la relación entre la resistencia de CA y la resistencia de CC se acerca a la mitad de la relación entre el radio y la profundidad de la piel.

Consulte el diagrama a continuación que muestra los conductores internos y externos de un cable coaxial. Dado que el efecto pelicular hace que una corriente a altas frecuencias fluya principalmente en la superficie de un conductor, se puede ver que esto reducirá el campo magnético dentro del cable, es decir, por debajo de la profundidad a la que fluye la mayor parte de la corriente. Se puede demostrar que esto tendrá un efecto menor en la autoinducción del propio cable; consulte Skilling ^[10] o Hayt ^[11] para un tratamiento matemático de este fenómeno.

La inductancia considerada en este contexto se refiere a un conductor desnudo, no a la inductancia de una bobina utilizada como elemento de circuito. La inductancia de una bobina está dominada por la inductancia mutua entre las espiras de la bobina, que aumenta su inductancia de acuerdo con el cuadrado del número de espiras. Sin embargo, cuando solo se trata de un solo cable, entonces, además de la inductancia externa que implica campos magnéticos fuera del cable (debido a la corriente total en el cable) como se ve en la región blanca de la figura siguiente, también hay un componente mucho más pequeño de inductancia interna debido a la parte del campo magnético dentro del propio cable, la región verde en la figura B. Ese pequeño componente de la inductancia se reduce cuando la corriente se concentra hacia la piel del conductor, es decir, cuando la profundidad de la piel no es mucho mayor que el radio del cable, como será el caso a frecuencias más altas.

En el caso de un solo cable, esta reducción pierde importancia a medida que el cable se hace más largo en comparación con su diámetro, y normalmente se descuida. Sin embargo, la presencia de un segundo conductor en el caso de una línea de transmisión reduce la extensión del campo magnético externo (y de la autoinductancia total) independientemente de la longitud del cable, de modo que la disminución de la inductancia debido al efecto pelicular puede seguir siendo importante. Por ejemplo, en el caso de un par trenzado telefónico, a continuación, la inductancia de los conductores disminuye sustancialmente a frecuencias más altas, donde el efecto pelicular se vuelve importante. Por otro lado, cuando el componente externo de la inductancia se magnifica debido a la geometría de una bobina (debido a la inductancia mutua entre las espiras), la importancia del componente de inductancia interna se eclipsa aún más y se ignora.

Cable coaxial

Sean las dimensiones a , b y c el radio del conductor interno, el radio interno del blindaje (conductor externo) y el radio externo del blindaje respectivamente, como se ve en la sección transversal de la figura  A a continuación.

Cuatro etapas del efecto pelicular en un cable coaxial que muestra el efecto sobre la inductancia. Los diagramas muestran una sección transversal del cable coaxial. Código de color: negro = vaina aislante general , marrón claro = conductor , blanco = dieléctrico , verde = corriente que entra en el diagrama, azul = corriente que sale del diagrama, líneas negras discontinuas con puntas de flecha = flujo magnético ( B ). El ancho de las líneas negras discontinuas tiene como objetivo mostrar la fuerza relativa del campo magnético integrado sobre la circunferencia en ese radio. Las cuatro etapas son A sin energía, B de baja frecuencia, C de frecuencia media y D de alta frecuencia. Hay tres regiones que pueden contener campos magnéticos inducidos: el conductor central, el dieléctrico y el conductor externo. En la etapa B , la corriente cubre los conductores de manera uniforme y hay un campo magnético significativo en las tres regiones. A medida que aumenta la frecuencia y se afianza el efecto pelicular ( C y D ), el campo magnético en la región dieléctrica no cambia, ya que es proporcional a la corriente total que fluye en el conductor central. En C , sin embargo, hay un campo magnético reducido en las secciones más profundas del conductor interno y las secciones externas del blindaje (conductor externo). Por lo tanto, hay menos energía almacenada en el campo magnético dada la misma corriente total, lo que corresponde a una inductancia reducida. A una frecuencia aún más alta, D , la profundidad de la piel es minúscula: toda la corriente se limita a la superficie de los conductores. El único campo magnético está en las regiones entre los conductores; solo permanece la inductancia externa .  

Para una corriente dada, la energía total almacenada en los campos magnéticos debe ser la misma que la energía eléctrica calculada atribuida a esa corriente que fluye a través de la inductancia del cable coaxial; esa energía es proporcional a la inductancia medida del cable.

El campo magnético dentro de un cable coaxial se puede dividir en tres regiones, cada una de las cuales contribuirá a la inductancia eléctrica observada en una longitud de cable. ^[12]

• La inductancia está asociada al campo magnético en la región con radio , la región dentro del conductor central. ${\displaystyle L_{\text{cen}}\,}$ ${\displaystyle r<a\,}$

• La inductancia está asociada al campo magnético en la región , la región entre los dos conductores (que contiene un dieléctrico, posiblemente aire). ${\displaystyle L_{\text{ext}}\,}$ ${\displaystyle a<r<b\,}$

• La inductancia está asociada con el campo magnético en la región , la región dentro del conductor de blindaje. ${\displaystyle L_{\text{shd}}\,}$ ${\displaystyle b<r<c\,}$

La inductancia eléctrica neta se debe a las tres contribuciones: $${\displaystyle L_{\text{total}}=L_{\text{cen}}+L_{\text{shd}}+L_{\text{ext}}\,}$$

${\displaystyle L_{\text{ext}}\,}$no se modifica por el efecto pelicular y se da mediante la fórmula frecuentemente citada para la inductancia L por longitud D de un cable coaxial: $${\displaystyle L/D={\frac {\mu _{0}}{2\pi }}\ln \left({\frac {b}{a}}\right)\,}$$

A bajas frecuencias, las tres inductancias están completamente presentes, de modo que . ${\displaystyle L_{\text{DC}}=L_{\text{cen}}+L_{\text{shd}}+L_{\text{ext}}\,}$

A altas frecuencias, sólo la región dieléctrica tiene flujo magnético, de modo que . ${\displaystyle L_{\infty }=L_{\text{ext}}\,}$

La mayoría de las discusiones sobre líneas de transmisión coaxial suponen que se utilizarán para frecuencias de radio, por lo que se suministran ecuaciones correspondientes únicamente al último caso.

A medida que aumenta el efecto pelicular, las corrientes se concentran cerca del exterior del conductor interno ( r  =  a ) y del interior del blindaje ( r  =  b ). Dado que esencialmente no hay corriente más profunda en el conductor interno, no hay campo magnético debajo de la superficie del conductor interno. Dado que la corriente en el conductor interno está equilibrada por la corriente opuesta que fluye en el interior del conductor externo, no hay campo magnético restante en el propio conductor externo donde . Solo contribuye a la inductancia eléctrica a estas frecuencias más altas. ${\displaystyle b<r<c\,}$ ${\displaystyle L_{\text{ext}}}$

Aunque la geometría es diferente, un par trenzado utilizado en líneas telefónicas se ve afectado de manera similar: a frecuencias más altas, la inductancia disminuye en más de un 20% como se puede ver en la siguiente tabla.

Cable telefónico

Datos de parámetros representativos para cable telefónico PIC calibre 24 a 21 °C (70 °F).

En Reeve se encuentran disponibles tablas más extensas y tablas para otros calibres, temperaturas y tipos. ^[13] Chen ^[14] proporciona los mismos datos en una forma parametrizada que, según afirma, se puede utilizar hasta 50 MHz.

Chen ^[14] da una ecuación de esta forma para el par trenzado telefónico: $${\displaystyle L(f)={\frac {\ell _{0}+\ell _{\infty }\left({\frac {f}{f_{m}}}\right)^{b}}{1+\left({\frac {f}{f_{m}}}\right)^{b}}}\,}$$

Efecto del material sobre la profundidad de la piel.

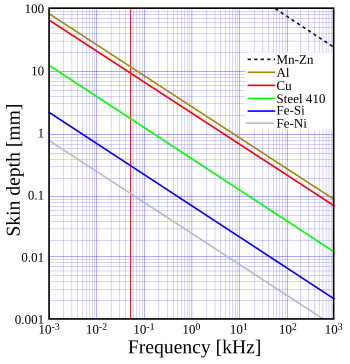
En un buen conductor, la profundidad de la piel es proporcional a la raíz cuadrada de la resistividad. Esto significa que los mejores conductores tienen una profundidad de piel reducida. La resistencia total del mejor conductor sigue siendo menor incluso con la profundidad de piel reducida. Sin embargo, el mejor conductor mostrará una relación más alta entre su resistencia de CA y CC, en comparación con un conductor de mayor resistividad. Por ejemplo, a 60 Hz, un conductor de cobre de 2000 MCM (1000 milímetros cuadrados) tiene un 23% más de resistencia que en CC. El mismo tamaño de conductor en aluminio tiene solo un 10% más de resistencia con 60 Hz de CA que con CC. ^[15]

La profundidad de la piel también varía como la raíz cuadrada inversa de la permeabilidad del conductor. En el caso del hierro, su conductividad es aproximadamente 1/7 de la del cobre. Sin embargo, al ser ferromagnético , su permeabilidad es aproximadamente 10.000 veces mayor. Esto reduce la profundidad de la piel del hierro a aproximadamente 1/38 de la del cobre, aproximadamente 220 micrómetros a 60 Hz. El cable de hierro es poco práctico para líneas de alimentación de CA (excepto para agregar resistencia mecánica al servir como núcleo para un conductor no ferromagnético como el aluminio). El efecto pelicular también reduce el espesor efectivo de las laminaciones en transformadores de potencia, lo que aumenta sus pérdidas.

Las varillas de hierro funcionan bien para la soldadura con corriente continua (CC), pero es difícil utilizarlas a frecuencias mucho más altas que 60 Hz. A unos pocos kilohertz, una varilla de soldadura de hierro se pondría al rojo vivo a medida que la corriente fluye a través de la resistencia de CA mucho mayor que resulta del efecto pelicular, con relativamente poca energía restante para el arco en sí. Solo se utilizan varillas no magnéticas para la soldadura de alta frecuencia.

A 1 megahercio la profundidad del efecto pelicular en suelo húmedo es de aproximadamente 5,0 m; en agua de mar es de aproximadamente 0,25 m. ^[16]

Mitigación

Un tipo de cable llamado hilo litz (del alemán Litzendraht , hilo trenzado) se utiliza para mitigar el efecto pelicular para frecuencias de unos pocos kilohercios a aproximadamente un megahercio. Consiste en una serie de hilos de alambre aislados entretejidos en un patrón cuidadosamente diseñado, de modo que el campo magnético general actúa por igual en todos los cables y hace que la corriente total se distribuya de manera uniforme entre ellos. Como el efecto pelicular tiene poco efecto en cada uno de los hilos delgados, el haz no sufre el mismo aumento de resistencia de CA que sufriría un conductor sólido de la misma área de sección transversal debido al efecto pelicular. ^[17]

El alambre litz se utiliza a menudo en los devanados de transformadores de alta frecuencia para aumentar su eficiencia mitigando tanto el efecto pelicular como el efecto de proximidad. Los transformadores de potencia grandes se enrollan con conductores trenzados de construcción similar al alambre litz, pero empleando una sección transversal más grande correspondiente a la mayor profundidad pelicular en las frecuencias de la red eléctrica. ^[18] Se ha demostrado que los hilos conductores compuestos de nanotubos de carbono ^[19] son ​​conductores para antenas desde frecuencias de onda media hasta microondas. A diferencia de los conductores de antena estándar, los nanotubos son mucho más pequeños que la profundidad pelicular, lo que permite el uso completo de la sección transversal del hilo, lo que da como resultado una antena extremadamente ligera.

Las líneas eléctricas aéreas de alto voltaje y alta corriente a menudo utilizan cables de aluminio con un núcleo de refuerzo de acero ; la mayor resistencia del núcleo de acero no tiene importancia, ya que está ubicado muy por debajo de la profundidad de la piel, donde esencialmente no fluye corriente alterna.

En aplicaciones donde circulan corrientes elevadas (hasta miles de amperios), los conductores sólidos suelen sustituirse por tubos, eliminando así la parte interior del conductor por donde circula poca corriente. Esto apenas afecta a la resistencia de CA, pero reduce considerablemente el peso del conductor. La alta resistencia pero el bajo peso de los tubos aumenta sustancialmente la capacidad de paso. Los conductores tubulares son típicos en los patios de distribución de energía eléctrica donde la distancia entre los aisladores de soporte puede ser de varios metros. Los tramos largos suelen presentar flechas físicas, pero esto no afecta al rendimiento eléctrico. Para evitar pérdidas, la conductividad del material del tubo debe ser alta.

En situaciones de alta corriente donde los conductores ( barras colectoras redondas o planas ) pueden tener entre 5 y 50 mm de espesor, el efecto pelicular también ocurre en curvas cerradas donde el metal se comprime dentro de la curva y se estira fuera de la curva. El camino más corto en la superficie interna da como resultado una resistencia menor, lo que hace que la mayor parte de la corriente se concentre cerca de la superficie de la curva interna. Esto causa un aumento de temperatura en esa región en comparación con el área recta (sin doblar) del mismo conductor. Un efecto pelicular similar ocurre en las esquinas de los conductores rectangulares (vistos en sección transversal), donde el campo magnético está más concentrado en las esquinas que en los lados. Esto da como resultado un rendimiento superior (es decir, mayor corriente con menor aumento de temperatura) de conductores anchos y delgados (por ejemplo, conductores de cinta ) en los que los efectos de las esquinas se eliminan de manera efectiva.

De ello se deduce que un transformador con un núcleo redondo será más eficiente que un transformador de potencia equivalente que tenga un núcleo cuadrado o rectangular del mismo material.

Los conductores sólidos o tubulares pueden ser plateados para aprovechar la mayor conductividad de la plata. Esta técnica se utiliza particularmente en frecuencias de VHF a microondas , donde la pequeña profundidad de la película requiere solo una capa muy fina de plata, lo que hace que la mejora en la conductividad sea muy rentable. El plateado se utiliza de manera similar en la superficie de las guías de ondas utilizadas para la transmisión de microondas. Esto reduce la atenuación de la onda que se propaga debido a las pérdidas resistivas que afectan a las corrientes parásitas que la acompañan; el efecto de película confina dichas corrientes parásitas a una capa superficial muy delgada de la estructura de la guía de ondas. El efecto de película en sí no se combate realmente en estos casos, pero la distribución de corrientes cerca de la superficie del conductor hace que el uso de metales preciosos (que tienen una resistividad menor) sea práctico. Aunque tiene una conductividad menor que el cobre y la plata, también se utiliza el dorado, porque a diferencia del cobre y la plata, no se corroe. Una capa delgada oxidada de cobre o plata tendría una conductividad baja y, por lo tanto, causaría grandes pérdidas de potencia, ya que la mayor parte de la corriente seguiría fluyendo a través de esta capa.

Recientemente, se ha demostrado que un método de superposición de materiales no magnéticos y ferromagnéticos con espesores a escala nanométrica mitiga la mayor resistencia del efecto pelicular para aplicaciones de muy alta frecuencia. ^[20] Una teoría de trabajo es que el comportamiento de los materiales ferromagnéticos en altas frecuencias da como resultado campos y/o corrientes que se oponen a los generados por materiales relativamente no magnéticos, pero se necesita más trabajo para verificar los mecanismos exactos. ^{[ cita requerida ]} Como han demostrado los experimentos, esto tiene el potencial de mejorar en gran medida la eficiencia de los conductores que operan en decenas de GHz o más. Esto tiene fuertes ramificaciones para las comunicaciones 5G . ^[20]

Ejemplos

Profundidad de la piel frente a frecuencia para algunos materiales a temperatura ambiente, la línea vertical roja indica una frecuencia de 50 Hz:

• Mn-Zn – ferrita magnéticamente blanda
• Al – aluminio metálico
• Cu – cobre metálico
• acero 410 – acero inoxidable magnético
• Fe-Si – acero eléctrico de grano orientado
• Fe-Ni – aleación permanente de alta permeabilidad (80%Ni-20%Fe)

Podemos derivar una fórmula práctica para la profundidad de la piel de la siguiente manera: $${\displaystyle {\begin{aligned}\delta &={\frac {1}{\alpha }}={\sqrt {{2\rho } \over {(2\pi f)(\mu _{0}\mu _{r})}}}\\&={\frac {1}{\sqrt {\pi f\mu \sigma }}}\approx 503\,{\sqrt {\frac {\rho }{\mu _{r}f}}}\approx 503\,{\frac {1}{\sqrt {\mu _{r}f\sigma }}},\end{aligned}}}$$

dónde

• ${\displaystyle \delta =}$La profundidad de la piel en metros
• ${\displaystyle \alpha =}$La atenuación en ${\displaystyle {\frac {Np}{m}}}$
• ${\displaystyle \mu _{0}=}$la permeabilidad del espacio libre
• ${\displaystyle \mu =}$la permeabilidad del medio
• ${\displaystyle \sigma =}$la conductividad del medio (para cobre, ${\displaystyle \sigma \approx }$ 58,5 × 10 ⁶  S/m )
• ${\displaystyle f=}$la frecuencia de la corriente en Hz

El oro es un buen conductor con una resistividad de2,44 × 10 ⁻⁸  Ω·m y es esencialmente no magnético: 1, por lo que su profundidad de piel a una frecuencia de 50 Hz viene dada por ${\displaystyle \mu _{r}=}$ $${\displaystyle \delta =503\,{\sqrt {\frac {2.44\cdot 10^{-8}}{1\cdot 50}}}=11.1\,\mathrm {mm} }$$

El plomo, por el contrario, es un conductor relativamente pobre (entre los metales) con una resistividad de2,2 × 10 ⁻⁷  Ω·m , aproximadamente 9 veces la del oro. Su profundidad de capa a 50 Hz también es de aproximadamente 33 mm, o veces la del oro. ${\displaystyle {\sqrt {9}}=3}$

Los materiales altamente magnéticos tienen una profundidad de capa reducida debido a su gran permeabilidad , como se señaló anteriormente para el caso del hierro, a pesar de su menor conductividad. Una consecuencia práctica la observan los usuarios de cocinas de inducción , donde algunos tipos de utensilios de cocina de acero inoxidable son inutilizables porque no son ferromagnéticos. ${\displaystyle \mu _{r}}$

A frecuencias muy altas, la profundidad de la piel de los buenos conductores se vuelve minúscula. Por ejemplo, la profundidad de la piel de algunos metales comunes a una frecuencia de 10 GHz (región de microondas) es inferior a un micrómetro :

Por tanto, en las frecuencias de microondas, la mayor parte de la corriente fluye en una zona extremadamente fina cerca de la superficie. Por tanto, las pérdidas óhmicas de las guías de ondas en las frecuencias de microondas dependen únicamente del revestimiento de la superficie del material. Por tanto, una capa de plata de 3  μm de espesor evaporada sobre un trozo de vidrio es un excelente conductor en esas frecuencias.

En el cobre, se puede observar que la profundidad de la piel disminuye según la raíz cuadrada de la frecuencia:

En Ingeniería Electromagnética , Hayt señala que en una central eléctrica, una barra colectora para corriente alterna a 60 Hz con un radio mayor a un tercio de pulgada (8 mm) es un desperdicio de cobre, ^[21] y en la práctica, las barras colectoras para corriente alterna pesada rara vez tienen más de media pulgada (12 mm) de espesor, excepto por razones mecánicas.

Ondas electromagnéticas

En las ondas electromagnéticas, la profundidad de la piel es la profundidad a la que la amplitud de los campos eléctricos y magnéticos se han reducido en . ^[22] La intensidad de la onda es proporcional al cuadrado de la amplitud y, por lo tanto, la profundidad a la que la intensidad ha disminuido en es En las guías de ondas , las pérdidas debido a las corrientes inducidas ocurren principalmente dentro de una profundidad de piel de la superficie. Por lo tanto, recubrir la superficie de una guía de ondas con un material que tenga una profundidad de piel baja reduce las pérdidas. ^[23] ${\displaystyle {\frac {1}{e}}}$ ${\displaystyle {\frac {1}{e}}}$ ${\displaystyle {\frac {\delta }{2}}.}$

Efecto anómalo en la piel

En el caso de frecuencias altas y temperaturas bajas, las fórmulas habituales para la profundidad pelicular no funcionan. Este efecto fue observado por primera vez por Heinz London en 1940, quien sugirió correctamente que se debe a la longitud media del recorrido libre de los electrones que alcanzan el rango de la profundidad pelicular clásica. ^[24] La teoría de Mattis-Bardeen fue desarrollada para este caso específico de metales y superconductores .

Véase también

• Efecto de proximidad (electromagnetismo)
• Corriente de Foucault
• Alambre litz
• Transformador
• Cocina por inducción
• Calentamiento por inducción
• Número de Reynolds magnético
• Regla de inductancia incremental de Wheeler , un método para estimar la resistencia del efecto pelicular

Notas

1. Nótese que la ecuación anterior para la densidad de corriente dentro del conductor en función de la profundidad se aplica a los casos en los que se cumple la aproximación habitual para la profundidad de la piel. En los casos extremos en los que no se cumple, la disminución exponencial con respecto a la profundidad de la piel aún se aplica a la magnitud de las corrientes inducidas, sin embargo, la parte imaginaria del exponente en esa ecuación y, por lo tanto, la velocidad de fase dentro del material, se modifican con respecto a esa ecuación.

Referencias

1. Lamb, Horace (1 de enero de 1883). "XIII. Sobre movimientos eléctricos en un conductor esférico". Philosophical Transactions of the Royal Society of London . 174 : 519–549. doi :10.1098/rstl.1883.0013. S2CID  111283238.
2. Fink, Donald G.; Beaty, H. Wayne (2000). Manual estándar para ingenieros eléctricos (14.ª edición). McGraw-Hill. págs. 2–50. ISBN 978-0-07-022005-8Estas fem son mayores en el centro que en la circunferencia, por lo que la diferencia de potencial tiende a establecer corrientes que se oponen a la corriente en el centro y la ayudan en la circunferencia .
3. Johnson, Howard; Graham, Martin (2003). Propagación de señales a alta velocidad. Magia negra avanzada (3.ª ed.). Prentice Hall. Págs. 58-78. ISBN 978-0-13-084408-8Para comprender el efecto piel , primero debes entender cómo funcionan las corrientes de Foucault...
4. Hayt, William H. (1989), Ingeniería electromagnética (5.ª ed.), McGraw-Hill, ISBN 978-0070274068
5. Vander Vorst, Rosen y Kotsuka (2006)
6. La fórmula que se muestra es algebraicamente equivalente a la fórmula que se encuentra en la página 130 de Jordan (1968, pág. 130).
7. Weeks, Walter L. (1981), Transmisión y distribución de energía eléctrica , Harper & Row, ISBN 978-0060469825
8. Terman 1943, pág. ??
9. Hayt (1981, pág. 303)
10. Skilling (1951, págs. 157-159)
11. Hayt (1981, págs. 434-439)
12. Hayt (1981, pág. 434)
13. Reeve (1995, pág. 558) harvtxt error: no target: CITEREFReeve1995 (help)
14. Chen (2004, pág. 26)
15. Fink, Donald G.; Beatty, H. Wayne, eds. (1978), Standard Handbook for Electrical Engineers (11.ª ed.), McGraw Hill, pág. Tabla 18-21
16. Popovic y Popovic 1999, pág. 385
17. Xi Nan y Sullivan 2005
18. Central Electricity Generating Board (1982). Práctica moderna de centrales eléctricas . Pergamon Press.
19. "Los nanotubos de carbono giratorios generan nuevas aplicaciones inalámbricas". Sciencedaily.com. 2009-03-09 . Consultado el 2011-11-08 .
20. Rahimi, A.; Yoon, Y.-K. (16 de marzo de 2016). "Estudio sobre conductores de nano superredes de Cu/Ni para reducir la pérdida de RF". IEEE Microwave and Wireless Components Letters . 26 (4): 258–260. doi :10.1109/LMWC.2016.2537780. ISSN  1531-1309. S2CID  30187468 . Consultado el 22 de diciembre de 2020 – a través de ResearchGate.
21. Hayt (1981, pág. 401)
22. Jackson (1999, pág. 353)
23. Feynman (1964, pág. 32-11)
24. RG Chambers, The Anomalous Skin Effect , Actas de la Royal Society de Londres, Serie A, Ciencias Físicas y Matemáticas, vol. 215, n.º 1123 (22 de diciembre de 1952), págs. 481–497 (17 páginas) https://www.jstor.org/stable/99095

• Chen, Walter Y. (2004), Conceptos básicos de redes domésticas , Prentice Hall, ISBN 978-0-13-016511-4
• Feynman, Richard P; Leighton, Robert B; Sands, Matthew (1964). Las conferencias Feynman sobre física, volumen 2. Addison-Wesley. ISBN 0-201-02117-X.
• Hayt, William (1981), Ingeniería electromagnética (4.ª ed.), McGraw-Hill, ISBN 978-0-07-027395-5
• Jackson, John David (1999), Electrodinámica clásica (3.ª ed.), Wiley, ISBN 978-0471309321
• Jordan, Edward Conrad (1968), Ondas electromagnéticas y sistemas radiantes , Prentice Hall, ISBN 978-0-13-249995-8
• Nahin, Paul J. Oliver Heaviside: Sabio en soledad . Nueva York: IEEE Press, 1988. ISBN 0-87942-238-6 . 
• Popovic, Zoya; Popovic, Branko (1999), Capítulo 20, El efecto de la piel, Introducción al electromagnetismo , Prentice-Hall, ISBN 978-0-201-32678-9
• Skilling, Hugh H. (1951), Líneas de transmisión eléctrica , McGraw-Hill
• Terman, FE (1943), Manual de ingenieros de radio , Nueva York: McGraw-Hill
• Vander Vorst, Andre; Rosen, Arye; Kotsuka, Youji (2006), Interacción de RF/microondas con tejidos biológicos , John Wiley and Sons, Inc., ISBN 978-0-471-73277-8
• Xi Nan; Sullivan, CR (2005). "Un modelo de permeabilidad complejo equivalente para bobinados de alambre litz". Cuadragésima Reunión Anual de la IAS. Acta de la Conferencia de Aplicaciones Industriales de 2005, 2005. Vol. 3. págs. 2229–2235. doi :10.1109/IAS.2005.1518758. ISBN 978-0-7803-9208-3. ISSN  0197-2618. S2CID  114947614.

Enlaces externos