Morfología matemática

Una forma (en azul) y su dilatación morfológica (en verde) y erosión (en amarillo) por un elemento estructurante en forma de rombo.

La morfología matemática ( MM ) es una teoría y técnica para el análisis y procesamiento de estructuras geométricas , basada en la teoría de conjuntos , la teoría de redes , la topología y las funciones aleatorias . MM se aplica más comúnmente a imágenes digitales , pero también se puede emplear en gráficos , mallas de superficie , sólidos y muchas otras estructuras espaciales.

MM introdujo conceptos topológicos y geométricos de espacio continuo , como tamaño, forma , convexidad , conectividad y distancia geodésica , tanto en espacios continuos como discretos . MM es también la base del procesamiento de imágenes morfológicas , que consta de un conjunto de operadores que transforman imágenes de acuerdo con las caracterizaciones anteriores.

Los operadores morfológicos básicos son erosión , dilatación , apertura y cierre .

MM se desarrolló originalmente para imágenes binarias y luego se extendió a funciones e imágenes en escala de grises . La generalización posterior para completar redes es ampliamente aceptada hoy como fundamento teórico del MM.

Historia

La Morfología Matemática fue desarrollada en 1964 gracias al trabajo colaborativo de Georges Matheron y Jean Serra , en la École des Mines de París , Francia . Matheron supervisó la tesis doctoral de Serra, dedicada a la cuantificación de características minerales a partir de secciones transversales delgadas , y este trabajo resultó en un enfoque práctico novedoso, así como avances teóricos en geometría integral y topología .

En 1968, el Centre de Morphologie Mathématique fue fundado por la École des Mines de Paris en Fontainebleau , Francia, dirigido por Matheron y Serra.

Durante el resto de la década de 1960 y la mayor parte de la década de 1970, MM se ocupó esencialmente de imágenes binarias , tratadas como conjuntos , y generó una gran cantidad de operadores y técnicas binarias : transformada de acierto o error , dilatación , erosión , apertura , cierre , granulometría. , adelgazamiento , esqueletización , erosión última, bisectriz condicional y otros. También se desarrolló un enfoque aleatorio, basado en modelos de imágenes novedosos. La mayor parte del trabajo de ese período se desarrolló en Fontainebleau.

Desde mediados de la década de 1970 hasta mediados de la de 1980, MM se generalizó también a funciones e imágenes en escala de grises . Además de extender los conceptos principales (como dilatación, erosión, etc.) a funciones, esta generalización produjo nuevos operadores, como gradientes morfológicos , transformación de sombrero de copa y Watershed (el principal enfoque de segmentación de MM ).

En las décadas de 1980 y 1990, el MM obtuvo un reconocimiento más amplio, a medida que los centros de investigación de varios países comenzaron a adoptar e investigar el método. MM comenzó a aplicarse a una gran cantidad de problemas y aplicaciones de imágenes, especialmente en el campo del filtrado no lineal de imágenes ruidosas.

En 1986, Serra generalizó aún más el MM, esta vez a un marco teórico basado en redes completas . Esta generalización aportó flexibilidad a la teoría, permitiendo su aplicación a un número mucho mayor de estructuras, incluidas imágenes en color, vídeos, gráficos , mallas , etc. Al mismo tiempo, Matheron y Serra también formularon una teoría para el filtrado morfológico , basada en la nuevo marco reticular.

Las décadas de 1990 y 2000 también vieron más avances teóricos, incluidos los conceptos de conexiones y nivelaciones .

En 1993 tuvo lugar en Barcelona , ​​España , el primer Simposio Internacional sobre Morfología Matemática (ISMM) . Desde entonces, los ISMM se organizan cada 2 o 3 años: Fontainebleau , Francia (1994); Atlanta , Estados Unidos (1996); Ámsterdam , Países Bajos (1998); Palo Alto , California , Estados Unidos (2000); Sídney , Australia (2002); París , Francia (2005); Río de Janeiro , Brasil (2007); Groninga , Países Bajos (2009); Intra ( Verbania ), Italia (2011); Upsala , Suecia (2013); Reikiavik , Islandia (2015); y Fontainebleau , Francia (2017).

Referencias

• "Introducción" de Pierre Soille, en (Serra et al. (Eds.) 1994), págs. 1-4.
• "Apéndice A: El 'Centre de Morphologie Mathématique', una descripción general" por Jean Serra, en (Serra et al. (Eds.) 1994), págs. 369-374.
• "Prólogo" en (Ronse et al. (Eds.) 2005)

Morfología binaria

En morfología binaria, una imagen se ve como un subconjunto de un espacio euclidiano o la cuadrícula entera , para alguna dimensión d . ${\displaystyle \mathbb {R} ^{d}}$ ${\displaystyle \mathbb {Z} ^{d}}$

Elemento estructurante

La idea básica en morfología binaria es sondear una imagen con una forma simple y predefinida, sacando conclusiones sobre cómo esta forma encaja o no con las formas de la imagen. Esta simple "sonda" se llama elemento estructurante y es en sí misma una imagen binaria (es decir, un subconjunto del espacio o cuadrícula).

A continuación se muestran algunos ejemplos de elementos estructurantes ampliamente utilizados (indicados por B ):

• Dejar ; B es un disco abierto de radio r , centrado en el origen. ${\displaystyle E=\mathbb {R} ^{2}}$
• Dejar ; B es un cuadrado de 3 × 3, es decir, B = {(−1, −1), (−1, 0), (−1, 1), (0, −1), (0, 0), ( 0, 1), (1, −1), (1, 0), (1, 1)}. ${\displaystyle E=\mathbb {Z} ^{2}}$
• Dejar ; B es la "cruz" dada por B = {(−1, 0), (0, −1), (0, 0), (0, 1), (1, 0)}. ${\displaystyle E=\mathbb {Z} ^{2}}$

Operadores básicos

Las operaciones básicas son operadores invariantes de desplazamiento ( invariantes de traducción ) fuertemente relacionados con la suma de Minkowski .

Sea E un espacio euclidiano o una cuadrícula de números enteros, y A una imagen binaria en E.

Erosión

La erosión del cuadrado azul oscuro por un disco, dando como resultado el cuadrado azul claro.

La erosión de la imagen binaria A por el elemento estructurante B está definida por

${\displaystyle A\ominus B=\{z\in E|B_{z}\subseteq A\},}$

donde B _z es la traslación de B por el vector z , es decir, , . ${\displaystyle B_{z}=\{b+z\mid b\in B\}}$ ${\displaystyle \forall z\in E}$

Cuando el elemento estructurante B tiene un centro (p. ej., B es un disco o un cuadrado), y este centro está situado en el origen de E , entonces la erosión de A por B puede entenderse como el lugar geométrico de los puntos alcanzados por el centro. de B cuando B se mueve dentro de A . Por ejemplo, la erosión de un cuadrado de lado 10, centrado en el origen, por un disco de radio 2, también centrado en el origen, es un cuadrado de lado 6 centrado en el origen.

La erosión de A por B también viene dada por la expresión . ${\displaystyle A\ominus B=\bigcap _{b\in B}A_{-b}}$

Aplicación de ejemplo: Supongamos que hemos recibido un fax de una fotocopia oscura. Todo parece escrito con un bolígrafo que sangra. El proceso de erosión permitirá que las líneas más gruesas se adelgacen y detecten el agujero dentro de la letra "o".

Dilatación

La dilatación del cuadrado azul oscuro por un disco, lo que da como resultado el cuadrado azul claro con esquinas redondeadas.

La dilatación de A por el elemento estructurante B está definida por

${\displaystyle A\oplus B=\bigcup _{b\in B}A_{b}.}$

La dilatación es conmutativa, también dada por . ${\displaystyle A\oplus B=B\oplus A=\bigcup _{a\in A}B_{a}}$

Si B tiene centro en el origen, como antes, entonces la dilatación de A por B puede entenderse como el lugar geométrico de los puntos cubiertos por B cuando el centro de B se mueve dentro de A. En el ejemplo anterior, la dilatación del cuadrado de lado 10 por el disco de radio 2 es un cuadrado de lado 14, con esquinas redondeadas, centrado en el origen. El radio de las esquinas redondeadas es 2.

La dilatación también se puede obtener mediante , donde B ^s denota la simetría de B , es decir, . ${\displaystyle A\oplus B=\{z\in E\mid (B^{s})_{z}\cap A\neq \varnothing \}}$ ${\displaystyle B^{s}=\{x\in E\mid -x\in B\}}$

Ejemplo de aplicación: la dilatación es la operación dual de la erosión. Las figuras que están muy ligeramente dibujadas se vuelven gruesas cuando se "dilatan". La forma más sencilla de describirlo es imaginar que el mismo fax/texto está escrito con un bolígrafo más grueso.

Apertura

La apertura del cuadrado azul oscuro mediante un disco, dando como resultado el cuadrado azul claro con esquinas redondeadas.

La apertura de A por B se obtiene por la erosión de A por B , seguida de la dilatación de la imagen resultante por B :

${\displaystyle A\circ B=(A\ominus B)\oplus B.}$

La apertura también está dada por , lo que significa que es el lugar de traslaciones del elemento estructurante B dentro de la imagen A . En el caso del cuadrado de lado 10, y un disco de radio 2 como elemento estructurante, la abertura es un cuadrado de lado 10 con esquinas redondeadas, donde el radio de las esquinas es 2. ${\displaystyle A\circ B=\bigcup _{B_{x}\subseteq A}B_{x}}$

Ejemplo de aplicación: supongamos que alguien ha escrito una nota en un papel que no está empapado y que parece como si a la escritura le estuvieran creciendo pequeñas raíces peludas por todas partes. La apertura esencialmente elimina las pequeñas fugas externas y restaura el texto. El efecto secundario es que completa las cosas. Los bordes afilados empiezan a desaparecer.

Clausura

El cierre de la forma azul oscuro (unión de dos cuadrados) por un disco, dando como resultado la unión de la forma azul oscuro y las áreas azul claro.

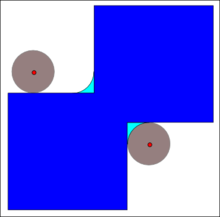
El cierre de A por B se obtiene por la dilatación de A por B , seguida de la erosión de la estructura resultante por B :

${\displaystyle A\bullet B=(A\oplus B)\ominus B.}$

El cierre también se puede obtener mediante , donde X ^c denota el complemento de X relativo a E (es decir, ). Lo anterior significa que el cierre es el complemento del lugar de traslaciones de la simétrica del elemento estructurante fuera de la imagen A. ${\displaystyle A\bullet B=(A^{c}\circ B^{s})^{c}}$ ${\displaystyle X^{c}=\{x\in E\mid x\notin X\}}$

Propiedades de los operadores básicos

A continuación se muestran algunas propiedades de los operadores morfológicos binarios básicos (dilatación, erosión, apertura y cierre):

• Son invariantes de traducción .
• Son crecientes , es decir, si , entonces , y , etc. ${\displaystyle A\subseteq C}$ ${\displaystyle A\oplus B\subseteq C\oplus B}$ ${\displaystyle A\ominus B\subseteq C\ominus B}$
• La dilatación es conmutativa : . ${\displaystyle A\oplus B=B\oplus A}$
• Si el origen de E pertenece al elemento estructurante B , entonces . ${\displaystyle A\ominus B\subseteq A\circ B\subseteq A\subseteq A\bullet B\subseteq A\oplus B}$
• La dilatación es asociativa , es decir, . Además, la erosión satisface . ${\displaystyle (A\oplus B)\oplus C=A\oplus (B\oplus C)}$ ${\displaystyle (A\ominus B)\ominus C=A\ominus (B\oplus C)}$
• La erosión y la dilatación satisfacen la dualidad . ${\displaystyle A\oplus B=(A^{c}\ominus B^{s})^{c}}$
• Abrir y cerrar satisfacen la dualidad . ${\displaystyle A\bullet B=(A^{c}\circ B^{s})^{c}}$
• La dilatación es distributiva sobre la unión establecida.
• La erosión es distributiva sobre una intersección determinada.
• La dilatación es una pseudoinversa de la erosión, y viceversa, en el siguiente sentido: si y sólo si . ${\displaystyle A\subseteq (C\ominus B)}$ ${\displaystyle (A\oplus B)\subseteq C}$
• La apertura y el cierre son idempotentes .
• La apertura es anti-extensiva, es decir, mientras que el cierre es extensivo , es decir ,. ${\displaystyle A\circ B\subseteq A}$ ${\displaystyle A\subseteq A\bullet B}$

Otros operadores y herramientas.

• Transformación impredecible
• Transformación de poda
• Esqueleto morfológico
• Filtrado por reconstrucción
• Erosiones finales y bisectrices condicionales.
• Granulometría
• Funciones de distancia geodésica

Morfología en escala de grises

Cuenca del gradiente de la imagen cardíaca

En morfología en escala de grises , las imágenes son funciones que asignan un espacio euclidiano o cuadrícula E , donde es el conjunto de reales , es un elemento mayor que cualquier número real y es un elemento menor que cualquier número real. ${\displaystyle \mathbb {R} \cup \{\infty ,-\infty \}}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \infty }$ ${\displaystyle -\infty }$

Los elementos estructurantes en escala de grises también son funciones del mismo formato, denominadas "funciones estructurantes".

Denotando una imagen por f ( x ), la función estructurante por b ( x ) y el soporte de b por B , la dilatación en escala de grises de f por b viene dada por

${\displaystyle (f\oplus b)(x)=\sup _{y\in B}[f(y)+b(x-y)],}$

donde "sup" denota el supremo .

De manera similar, la erosión de f por b viene dada por

${\displaystyle (f\ominus b)(x)=\inf _{y\in B}[f(y)-b(y-x)],}$

donde "inf" denota el mínimo .

Al igual que en la morfología binaria, la apertura y el cierre están dados respectivamente por

${\displaystyle f\circ b=(f\ominus b)\oplus b,}$

${\displaystyle f\bullet b=(f\oplus b)\ominus b.}$

Funciones de estructuración plana.

Es habitual utilizar elementos estructurantes planos en aplicaciones morfológicas. Las funciones de estructuración plana son funciones b ( x ) en la forma

${\displaystyle b(x)={\begin{cases}0,&x\in B,\\-\infty &{\text{otherwise}},\end{cases}}}$

dónde . ${\displaystyle B\subseteq E}$

En este caso, la dilatación y la erosión están muy simplificadas y vienen dadas respectivamente por

${\displaystyle (f\oplus b)(x)=\sup _{z\in B^{s}}f(x+z),}$

${\displaystyle (f\ominus b)(x)=\inf _{z\in B}f(x+z).}$

En el caso discreto y acotado ( E es una cuadrícula y B está acotado), los operadores supremo e mínimo se pueden reemplazar por el máximo y el mínimo . Por lo tanto, la dilatación y la erosión son casos particulares de filtros de estadísticas de orden , donde la dilatación devuelve el valor máximo dentro de una ventana en movimiento (la simetría del soporte de la función estructurante B ) , y la erosión devuelve el valor mínimo dentro de la ventana en movimiento B.

En el caso de un elemento estructurante plano, los operadores morfológicos dependen únicamente del orden relativo de los valores de los píxeles , independientemente de sus valores numéricos, y por lo tanto son especialmente adecuados para el procesamiento de imágenes binarias e imágenes en escala de grises cuya función de transferencia de luz se desconoce.

Otros operadores y herramientas.

• gradientes morfológicos
• Transformación de sombrero de copa
• Algoritmo de cuenca

Al combinar estos operadores, se pueden obtener algoritmos para muchas tareas de procesamiento de imágenes, como detección de características , segmentación de imágenes , nitidez de imágenes , filtrado de imágenes y clasificación . En esta línea también se debería profundizar en la Morfología Continua ^[1]

Morfología matemática en celosías completas.

Las redes completas son conjuntos parcialmente ordenados , donde cada subconjunto tiene un mínimo y un supremo . En particular, contiene un elemento mínimo y un elemento mayor (también denominado "universo").

Adjunciones (dilatación y erosión)

Sea una red completa, con ínfimo y supremo simbolizados por y , respectivamente. Su universo y su mínimo elemento están simbolizados por U y , respectivamente. Además, sea una colección de elementos de L . ${\displaystyle (L,\leq )}$ ${\displaystyle \wedge }$ ${\displaystyle \vee }$ ${\displaystyle \emptyset }$ ${\displaystyle \{X_{i}\}}$

Una dilatación es cualquier operador que se distribuye sobre el supremo y conserva el mínimo elemento. Es decir: ${\displaystyle \delta \colon L\rightarrow L}$

• ${\displaystyle \bigvee _{i}\delta (X_{i})=\delta \left(\bigvee _{i}X_{i}\right)}$,
• ${\displaystyle \delta (\emptyset )=\emptyset }$.

Una erosión es cualquier operador que se distribuye sobre el mínimo y preserva el universo. Es decir: ${\displaystyle \varepsilon \colon L\rightarrow L}$

• ${\displaystyle \bigwedge _{i}\varepsilon (X_{i})=\varepsilon \left(\bigwedge _{i}X_{i}\right)}$,
• ${\displaystyle \varepsilon (U)=U}$.

Las dilataciones y erosiones forman conexiones de Galois . Es decir, por cada dilatación existe una y sólo una erosión que satisface ${\displaystyle \delta }$ ${\displaystyle \varepsilon }$

${\displaystyle X\leq \varepsilon (Y)\Leftrightarrow \delta (X)\leq Y}$

para todos . ${\displaystyle X,Y\in L}$

De manera similar, por cada erosión hay una y sólo una dilatación que satisface la conexión anterior.

Además, si dos operadores satisfacen la conexión, entonces debe haber una dilatación y una erosión. ${\displaystyle \delta }$ ${\displaystyle \varepsilon }$

Los pares de erosiones y dilataciones que satisfacen la conexión anterior se denominan "conjunciones", y se dice que la erosión es la erosión adjunta de la dilatación, y viceversa.

Abriendo y cerrando

Para cada conjunción , la apertura morfológica y el cierre morfológico se definen de la siguiente manera: ${\displaystyle (\varepsilon ,\delta )}$ ${\displaystyle \gamma \colon L\to L}$ ${\displaystyle \phi \colon L\to L}$

${\displaystyle \gamma =\delta \varepsilon ,}$

${\displaystyle \phi =\varepsilon \delta .}$

La apertura y el cierre morfológicos son casos particulares de apertura algebraica (o simplemente apertura) y cierre algebraico (o simplemente cierre). Las aperturas algebraicas son operadores en L que son idempotentes, crecientes y antiextensivo. Los cierres algebraicos son operadores en L que son idempotentes, crecientes y extensivos.

Casos particulares

La morfología binaria es un caso particular de morfología reticular, donde L es el conjunto potencia de E (espacio euclidiano o cuadrícula), es decir, L es el conjunto de todos los subconjuntos de E , y es la inclusión del conjunto . En este caso, el mínimo se establece en intersección y el supremo se establece en unión . ${\displaystyle \leq }$

De manera similar, la morfología en escala de grises es otro caso particular, donde L es el conjunto de funciones que asignan E a , y , y , son el orden puntual, supremo e mínimo, respectivamente. Es decir, si f y g son funciones en L , entonces si y sólo si ; el mínimo está dado por ; y el supremo está dado por . ${\displaystyle \mathbb {R} \cup \{\infty ,-\infty \}}$ ${\displaystyle \leq }$ ${\displaystyle \vee }$ ${\displaystyle \wedge }$ ${\displaystyle f\leq g}$ ${\displaystyle f(x)\leq g(x),\forall x\in E}$ ${\displaystyle f\wedge g}$ ${\displaystyle (f\wedge g)(x)=f(x)\wedge g(x)}$ ${\displaystyle f\vee g}$ ${\displaystyle (f\vee g)(x)=f(x)\vee g(x)}$

Ver también

• Transformada H-máxima

Notas

1. G. Sapiro, R. Kimmel, D. Shaked, B. Kimia y AM Bruckstein. Implementación de morfología de escala continua mediante evolución de curvas. Reconocimiento de patrones, 26(9):1363–1372, 1993.

Referencias

• Análisis de imágenes y morfología matemática de Jean Serra, ISBN  0-12-637240-3 (1982)
• Análisis de imágenes y morfología matemática, volumen 2: avances teóricos de Jean Serra, ISBN 0-12-637241-1 (1988) 
• Introducción al procesamiento de imágenes morfológicas por Edward R. Dougherty, ISBN 0-8194-0845-X (1992) 
• Análisis de Imágenes Morfológicas; Principios y aplicaciones de Pierre Soille, ISBN 3-540-65671-5 (1999), 2.ª edición (2003) 
• Morfología matemática y su aplicación al procesamiento de señales , J. Serra y Ph. Salembier (Eds.), actas del 1er taller internacional sobre morfología matemática y sus aplicaciones al procesamiento de señales (ISMM'93), ISBN 84-7653-271-7 (1993) 
• Morfología matemática y sus aplicaciones al procesamiento de imágenes , J. Serra y P. Soille (Eds.), actas del segundo simposio internacional sobre morfología matemática (ISMM'94), ISBN 0-7923-3093-5 (1994) 
• Morfología matemática y sus aplicaciones al procesamiento de imágenes y señales , Henk JAM Heijmans y Jos BTM Roerdink (Eds.), actas del cuarto simposio internacional sobre morfología matemática (ISMM'98), ISBN 0-7923-5133-9 (1998) 
• Morfología matemática: 40 años después , Christian Ronse, Laurent Najman y Etienne Decencière (Eds.), ISBN 1-4020-3442-3 (2005) 
• Morfología matemática y sus aplicaciones al procesamiento de señales e imágenes , Gerald JF Banon, Junior Barrera, Ulisses M. Braga-Neto (Eds.), actas del octavo simposio internacional sobre morfología matemática (ISMM'07), ISBN 978-85-17 -00032-4 (2007) 
• Morfología matemática: de la teoría a las aplicaciones , Laurent Najman y Hugues Talbot (Eds). ISTE-Wiley. ISBN 978-1-84821-215-2 . (520 págs.) Junio ​​de 2010 

enlaces externos

• Curso online sobre morfología matemática, a cargo de Jean Serra (en inglés, francés y español)
• Centro de Morfología Matemática, Escuela de Minas de París
• Historia de la Morfología Matemática, por Georges Matheron y Jean Serra
• Morphology Digest, un boletín sobre morfología matemática, por Pierre Soille
• Conferencias sobre procesamiento de imágenes: una colección de 18 conferencias en formato pdf de la Universidad de Vanderbilt. Las conferencias 16 a 18 son sobre morfología matemática, por Alan Peters
• Morfología Matemática; de conferencias sobre visión por computadora, por Robyn Owens
• SMIL: una biblioteca de imágenes morfológicas simple (pero eficiente) (de la Ecole des Mines de Paris)
• Biblioteca gratuita de procesamiento de imágenes optimizadas SIMD
• Demostración del subprograma de Java
• FILTROS: una biblioteca gratuita de procesamiento de imágenes de código abierto
• Erosiones, dilataciones, aperturas y cierres morfológicos rápidos.
• Análisis morfológico de neuronas mediante Matlab.