
Un cuadrante es un instrumento utilizado para medir ángulos de hasta 90° . Se podían utilizar diferentes versiones de este instrumento para calcular diversas lecturas, como la longitud , la latitud y la hora del día . Su uso registrado más antiguo fue en la antigua India en tiempos del Rigvédico por Rishi Atri para observar un eclipse solar. [1] [2] Luego fue propuesto por Ptolomeo como un mejor tipo de astrolabio . [3] Posteriormente, los astrónomos musulmanes medievales produjeron varias variaciones diferentes del instrumento . Los cuadrantes murales fueron instrumentos astronómicos importantes en los observatorios europeos del siglo XVIII , estableciendo un uso para la astronomía posicional .
El término cuadrante , que significa un cuarto, se refiere al hecho de que las primeras versiones del instrumento derivaban de los astrolabios. El cuadrante condensaba el funcionamiento del astrolabio en un área de un cuarto del tamaño de la esfera del astrolabio; era esencialmente un cuarto de un astrolabio.


Durante la época del Rigveda en la antigua India, se utilizaban cuadrantes llamados "Tureeyam" para medir la extensión de un gran eclipse solar . El uso de un Tureeyam para observar un eclipse solar por parte de Rishi Atri se describe en el quinto mandala del Rigveda , [1] [2] probablemente entre los años 1500 y 1000 a. C. [4]
Los primeros relatos sobre un cuadrante también provienen del Almagesto de Ptolomeo , alrededor del año 150 d. C. En él, describió un "pedestal" que podía medir la altitud del sol del mediodía proyectando la sombra de una estaca sobre un arco graduado de 90 grados. [5] Este cuadrante era diferente a las versiones posteriores del instrumento; era más grande y constaba de varias partes móviles. La versión de Ptolomeo era un derivado del astrolabio y el propósito de este dispositivo rudimentario era medir el ángulo meridiano del sol.
Los astrónomos islámicos de la Edad Media mejoraron estas ideas y construyeron cuadrantes por todo Oriente Medio, en observatorios como Marageh , Rey y Samarcanda . Al principio, estos cuadrantes solían ser muy grandes y estacionarios, y podían rotarse en cualquier dirección para obtener tanto la altitud como el acimut de cualquier cuerpo celeste. [5] A medida que los astrónomos islámicos avanzaban en la teoría astronómica y la precisión de las observaciones, se les atribuye el desarrollo de cuatro tipos diferentes de cuadrantes durante la Edad Media y más allá. El primero de ellos, el cuadrante seno , fue inventado por Muhammad ibn Musa al-Khwarizmi en el siglo IX en la Casa de la Sabiduría en Bagdad. [6] : 128 Los otros tipos eran el cuadrante universal, el cuadrante horario y el cuadrante astrolabio.
Durante la Edad Media, el conocimiento de estos instrumentos se extendió a Europa. En el siglo XIII, el astrónomo judío Jacob ben Machir ibn Tibbon fue crucial en el desarrollo del cuadrante. [7] Era un astrónomo experto y escribió varios volúmenes sobre el tema, incluido un influyente libro que detalla cómo construir y usar una versión mejorada del cuadrante. El cuadrante que inventó llegó a conocerse como novus quadrans o nuevo cuadrante. [8] Este dispositivo fue revolucionario porque fue el primer cuadrante que se construyó sin varias partes móviles y, por lo tanto, podía ser mucho más pequeño y portátil.
Los manuscritos hebreos de Tibbon fueron traducidos al latín y mejorados por el erudito danés Peter Nightingale varios años después. [9] [10] Debido a la traducción, Tibbon, o Prophatius Judaeus como era conocido en latín, se convirtió en un nombre influyente en astronomía. Su nuevo cuadrante se basó en la idea de que la proyección estereográfica que define un astrolabio planisférico todavía puede funcionar si las partes del astrolabio se pliegan en un solo cuadrante. [11] El resultado fue un dispositivo que era mucho más barato, más fácil de usar y más portátil que un astrolabio estándar. El trabajo de Tibbon tuvo un gran alcance e influyó en Copérnico , Christopher Clavius y Erasmus Reinhold ; y su manuscrito fue mencionado en la Divina Comedia de Dante . [7]
A medida que el cuadrante se hizo más pequeño y, por lo tanto, más portátil, pronto se comprendió su valor para la navegación. El primer uso documentado del cuadrante para navegar en el mar es de 1461, por Diogo Gomes . [12] Los marineros comenzaron midiendo la altura de Polaris para determinar su latitud. Esta aplicación de los cuadrantes generalmente se atribuye a los marineros árabes que comerciaban a lo largo de la costa este de África y a menudo viajaban fuera de la vista de la tierra. Pronto se volvió más común medir la altura del sol en un momento dado debido al hecho de que Polaris no es visible al sur del ecuador.
En 1618, el matemático inglés Edmund Gunter adaptó aún más el cuadrante con una invención que llegó a conocerse como el cuadrante de Gunter. [13] Este cuadrante de bolsillo fue revolucionario porque estaba inscrito con proyecciones de los trópicos, el ecuador, el horizonte y la eclíptica. Con las tablas correctas, se podía utilizar el cuadrante para encontrar la hora, la fecha, la duración del día o la noche, la hora de salida y puesta del sol y el meridiano. El cuadrante de Gunter era extremadamente útil, pero tenía sus inconvenientes; las escalas solo se aplicaban a una cierta latitud, por lo que el uso del instrumento estaba limitado en el mar.

Existen varios tipos de cuadrantes:
También se pueden clasificar en: [15]
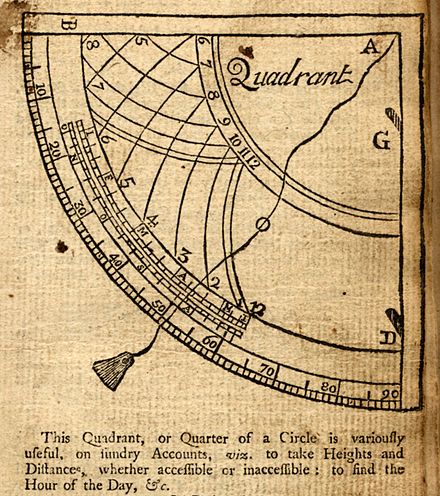

El cuadrante geométrico es un panel de un cuarto de círculo, generalmente de madera o latón. Las marcas en la superficie pueden estar impresas en papel y pegadas a la madera o pintadas directamente sobre la superficie. Los instrumentos de viento metal tenían sus marcas grabadas directamente en el latón.
Los primeros ejemplos de navegación marítima se encontraron alrededor de 1460. No estaban graduados en grados, sino que tenían las latitudes de los destinos más comunes directamente escritas en el extremo. Cuando se utilizaban, el navegante navegaba hacia el norte o el sur hasta que el cuadrante indicaba que estaba en la latitud del destino, giraba en la dirección del destino y navegaba hacia él manteniendo un rumbo de latitud constante. Después de 1480, se fabricaron más instrumentos con extremos graduados en grados. [21]
A lo largo de un borde había dos miras que formaban una alidada . Una plomada estaba suspendida por una cuerda desde el centro del arco en la parte superior.
Para medir la altura de una estrella, el observador la observaba a través de la mira y sostenía el cuadrante de manera que el plano del instrumento estuviera vertical. La plomada se dejaba colgar verticalmente y la línea indicaba la lectura en las graduaciones del arco . No era raro que una segunda persona tomara la lectura mientras la primera se concentraba en observar y sostener el instrumento en la posición adecuada.
La precisión del instrumento estaba limitada por su tamaño y por el efecto que el viento o el movimiento del observador tendrían sobre la plomada. Para los navegantes que se encontraban en la cubierta de un barco en movimiento, estas limitaciones podían ser difíciles de superar.

Para evitar tener que mirar directamente al sol para medir su altitud, los navegantes podían sostener el instrumento frente a ellos con el sol a su lado. Al hacer que la veleta de observación orientada hacia el sol proyectara su sombra sobre la veleta de observación inferior, era posible alinear el instrumento con el sol. Habría que tener cuidado para asegurarse de que se determinara la altitud del centro del sol. Esto podría hacerse promediando las elevaciones de la umbra superior e inferior en la sombra.
Para realizar mediciones de la altitud del sol, se desarrolló un cuadrante de observación posterior. [21]
Con un cuadrante de este tipo, el observador veía el horizonte desde una veleta (C en la figura de la derecha) a través de una ranura en la veleta del horizonte (B). Esto aseguraba que el instrumento estuviera nivelado. El observador movía la veleta de sombra (A) a una posición en la escala graduada de modo que su sombra pareciera coincidir con el nivel del horizonte en la veleta del horizonte. Este ángulo era la elevación del sol.
Los cuadrantes de gran tamaño se utilizaban para realizar mediciones astronómicas, en particular para determinar la altitud de los objetos celestes . Podían ser instalaciones permanentes, como los cuadrantes murales . Los cuadrantes más pequeños podían moverse. Al igual que los sextantes astronómicos similares , podían utilizarse en un plano vertical o ajustarse a cualquier plano.
Colocados sobre un pedestal u otro soporte, podrían usarse para medir la distancia angular entre dos objetos celestes.
Los detalles sobre su construcción y uso son esencialmente los mismos que los de los sextantes astronómicos ; consulte ese artículo para obtener más detalles.
Marina: Se utilizaba para medir la elevación de los cañones de los barcos. El cuadrante debía colocarse en el muñón de cada cañón para poder juzgar el alcance, después de la carga. La lectura se tomaba en el punto más alto del balanceo del barco, se ajustaba el cañón y se verificaba, nuevamente en el punto más alto del balanceo, y se pasaba al siguiente cañón, hasta que todos los que iban a disparar estuvieran listos. Se informaba al artillero del barco, quien a su vez informaba al capitán... Puede disparar cuando esté listo... en el siguiente balanceo alto, se dispararía el cañón.
En aplicaciones más modernas, el cuadrante se fija al anillo de apoyo o a un cañón naval grande para alinearlo con los puntos de referencia soldados a la cubierta del barco. Esto se hace para garantizar que el disparo del cañón no haya "deformado la cubierta". También se verifica una superficie plana en la caseta del cañón o la torreta de montaje con respecto a los puntos de referencia, para garantizar que los cojinetes grandes y/o las pistas de los cojinetes no hayan cambiado... para "calibrar" el cañón.
Durante la Edad Media, los fabricantes solían añadir detalles personalizados para impresionar a la persona a la que estaba destinado el cuadrante. En los espacios grandes y sin uso del instrumento, se solía añadir un sigilo o una insignia para indicar que el instrumento era propiedad de una persona importante o que el propietario era leal a ella. [22]
Por cierto, los préstamos indoarios de Mitanni confirman la fecha del Rig Veda de ca. 1200-1000 a. C. El Rig Veda es un texto de la Edad del Bronce tardía, por lo tanto de antes del 1000 a. C. Sin embargo, las palabras de Mitanni tienen una forma de indoario que es ligeramente más antigua que eso... Claramente, el Rig Veda no puede ser anterior a ca. 1400, y teniendo en cuenta un período necesario para el cambio lingüístico, puede que no sea mucho más antiguo que ca. 1200 a. C.