Ecuación de onda acústica

Ecuación para la propagación de ondas sonoras a través de un medio.

En física , la ecuación de ondas acústicas es una ecuación diferencial parcial de segundo orden que gobierna la propagación de ondas acústicas a través de un medio material , respectivamente. un campo de ondas estacionarias . La ecuación describe la evolución de la presión acústica p o la velocidad de la partícula u en función de la posición x y el tiempo t . Una forma simplificada (escalar) de la ecuación describe ondas acústicas en una sola dimensión espacial, mientras que una forma más general describe ondas en tres dimensiones. Las ondas que se propagan en una dirección predefinida también se pueden calcular utilizando una ecuación de onda unidireccional de primer orden .

Para medios con pérdidas, es necesario aplicar modelos más complejos para tener en cuenta la atenuación dependiente de la frecuencia y la velocidad de fase. Dichos modelos incluyen ecuaciones de ondas acústicas que incorporan términos de derivadas fraccionarias ; consulte también el artículo sobre atenuación acústica o el documento de estudio. ^[1]

en una dimensión

Ecuación

La ecuación de onda que describe un campo de onda estacionaria en una dimensión (posición ) es ${\displaystyle x}$

${\displaystyle {\partial ^{2}p \over \partial x^{2}}-{1 \over c^{2}}{\partial ^{2}p \over \partial t^{2}}=0,}$

¿Dónde está la presión acústica (la desviación local de la presión ambiental) y dónde está la velocidad del sonido ? ^[2] ${\displaystyle p}$ ${\displaystyle c}$

Solución

Siempre que la velocidad sea constante, no dependiente de la frecuencia (el caso sin dispersión), entonces la solución más general es ${\displaystyle c}$

${\displaystyle p=f(ct-x)+g(ct+x)}$

donde y son dos funciones cualesquiera dos veces diferenciables. Esto puede representarse como la superposición de dos formas de onda de perfil arbitrario, una ( ) viajando hacia arriba en el eje x y la otra ( ) hacia abajo por el eje x a la velocidad . El caso particular de una onda sinusoidal que viaja en una dirección se obtiene eligiendo que sea una sinusoide y la otra sea cero, dando ${\displaystyle f}$ ${\displaystyle g}$ ${\displaystyle f}$ ${\displaystyle g}$ ${\displaystyle c}$ ${\displaystyle f}$ ${\displaystyle g}$

${\displaystyle p=p_{0}\sin(\omega t\mp kx)}$.

donde es la frecuencia angular de la onda y es su número de onda . ${\displaystyle \omega }$ ${\displaystyle k}$

Derivación

Derivación de la ecuación de la onda acústica.

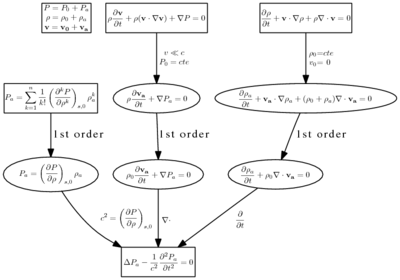
La derivación de la ecuación de onda implica tres pasos: derivación de la ecuación de estado, la ecuación de continuidad unidimensional linealizada y la ecuación de fuerza unidimensional linealizada.

La ecuación de estado ( ley de los gases ideales )

${\displaystyle PV=nRT}$

En un proceso adiabático , la presión P en función de la densidad se puede linealizar a ${\displaystyle \rho }$

${\displaystyle P=C\rho \,}$

donde C es una constante. Dividiendo la presión y la densidad en sus componentes media y total y observando que : ${\displaystyle C={\frac {\partial P}{\partial \rho }}}$

${\displaystyle P-P_{0}=\left({\frac {\partial P}{\partial \rho }}\right)(\rho -\rho _{0})}$.

El módulo de volumen adiabático de un fluido se define como

${\displaystyle B=\rho _{0}\left({\frac {\partial P}{\partial \rho }}\right)_{adiabatic}}$

que da el resultado

${\displaystyle P-P_{0}=B{\frac {\rho -\rho _{0}}{\rho _{0}}}}$.

La condensación, s , se define como el cambio de densidad para una densidad de fluido ambiental determinada.

${\displaystyle s={\frac {\rho -\rho _{0}}{\rho _{0}}}}$

La ecuación de estado linealizada se convierte en

${\displaystyle p=Bs\,}$donde p es la presión acústica ( ). ${\displaystyle P-P_{0}}$

La ecuación de continuidad (conservación de masa) en una dimensión es

${\displaystyle {\frac {\partial \rho }{\partial t}}+{\frac {\partial }{\partial x}}(\rho u)=0}$.

Donde u es la velocidad del flujo del fluido. Nuevamente se debe linealizar la ecuación y dividir las variables en componentes medios y variables.

${\displaystyle {\frac {\partial }{\partial t}}(\rho _{0}+\rho _{0}s)+{\frac {\partial }{\partial x}}(\rho _{0}u+\rho _{0}su)=0}$

Reordenando y observando que la densidad ambiental cambia sin tiempo ni posición y que la condensación multiplicada por la velocidad es un número muy pequeño:

${\displaystyle {\frac {\partial s}{\partial t}}+{\frac {\partial }{\partial x}}u=0}$

La ecuación de fuerza de Euler (conservación del impulso) es el último componente necesario. En una dimensión la ecuación es:

${\displaystyle \rho {\frac {Du}{Dt}}+{\frac {\partial P}{\partial x}}=0}$,

donde representa la derivada convectiva, sustancial o material , que es la derivada en un punto que se mueve junto con el medio en lugar de en un punto fijo. ${\displaystyle D/Dt}$

Linealizando las variables:

${\displaystyle (\rho _{0}+\rho _{0}s)\left({\frac {\partial }{\partial t}}+u{\frac {\partial }{\partial x}}\right)u+{\frac {\partial }{\partial x}}(P_{0}+p)=0}$.

Reorganizando y descuidando los términos pequeños, la ecuación resultante se convierte en la ecuación de Euler unidimensional linealizada:

${\displaystyle \rho _{0}{\frac {\partial u}{\partial t}}+{\frac {\partial p}{\partial x}}=0}$.

Tomando la derivada temporal de la ecuación de continuidad y la derivada espacial de la ecuación de fuerza se obtiene:

${\displaystyle {\frac {\partial ^{2}s}{\partial t^{2}}}+{\frac {\partial ^{2}u}{\partial x\partial t}}=0}$

${\displaystyle \rho _{0}{\frac {\partial ^{2}u}{\partial x\partial t}}+{\frac {\partial ^{2}p}{\partial x^{2}}}=0}$.

Multiplicando el primero por , restando los dos y sustituyendo la ecuación de estado linealizada, ${\displaystyle \rho _{0}}$

${\displaystyle -{\frac {\rho _{0}}{B}}{\frac {\partial ^{2}p}{\partial t^{2}}}+{\frac {\partial ^{2}p}{\partial x^{2}}}=0}$.

El resultado final es

${\displaystyle {\partial ^{2}p \over \partial x^{2}}-{1 \over c^{2}}{\partial ^{2}p \over \partial t^{2}}=0}$

¿ Dónde está la velocidad de propagación? ${\displaystyle c={\sqrt {\frac {B}{\rho _{0}}}}}$

En tres dimensiones

Ecuación

Feynman ^[3] proporciona una derivación de la ecuación de onda para el sonido en tres dimensiones como

${\displaystyle \nabla ^{2}p-{1 \over c^{2}}{\partial ^{2}p \over \partial t^{2}}=0,}$

donde es el operador de Laplace , es la presión acústica (la desviación local de la presión ambiental) y es la velocidad del sonido . ${\displaystyle \nabla ^{2}}$ ${\displaystyle p}$ ${\displaystyle c}$

Una ecuación de onda similar pero para el campo vectorial , la velocidad de la partícula viene dada por

${\displaystyle \nabla ^{2}\mathbf {u} \;-{1 \over c^{2}}{\partial ^{2}\mathbf {u} \; \over \partial t^{2}}=0}$.

En algunas situaciones, es más conveniente resolver la ecuación de onda para un potencial de velocidad de campo escalar abstracto que tiene la forma

${\displaystyle \nabla ^{2}\Phi -{1 \over c^{2}}{\partial ^{2}\Phi \over \partial t^{2}}=0}$

y luego derivar las cantidades físicas velocidad de las partículas y presión acústica mediante las ecuaciones (o definición, en el caso de la velocidad de las partículas):

${\displaystyle \mathbf {u} =\nabla \Phi \;}$,

${\displaystyle p=-\rho {\partial \over \partial t}\Phi }$.

Solución

Las siguientes soluciones se obtienen separando variables en diferentes sistemas de coordenadas. Son soluciones fasoriales , es decir, tienen un factor implícito de dependencia del tiempo de dónde está la frecuencia angular . La dependencia explícita del tiempo está dada por ${\displaystyle e^{i\omega t}}$ ${\displaystyle \omega =2\pi f}$

${\displaystyle p(r,t,k)=\operatorname {Real} \left[p(r,k)e^{i\omega t}\right]}$

Aquí está el número de onda . ${\displaystyle k=\omega /c\ }$

Coordenadas cartesianas

${\displaystyle p(r,k)=Ae^{\pm ikr}}$.

Coordenadas cilíndricas

${\displaystyle p(r,k)=AH_{0}^{(1)}(kr)+\ BH_{0}^{(2)}(kr)}$.

donde las aproximaciones asintóticas a las funciones de Hankel , cuando , son ${\displaystyle kr\rightarrow \infty }$

${\displaystyle H_{0}^{(1)}(kr)\simeq {\sqrt {\frac {2}{\pi kr}}}e^{i(kr-\pi /4)}}$

${\displaystyle H_{0}^{(2)}(kr)\simeq {\sqrt {\frac {2}{\pi kr}}}e^{-i(kr-\pi /4)}}$.

Coordenadas esféricas

${\displaystyle p(r,k)={\frac {A}{r}}e^{\pm ikr}}$.

Dependiendo de la convención de Fourier elegida, una de ellas representa una onda viajera hacia afuera y la otra una onda viajera hacia adentro no física. La onda de solución que viaja hacia adentro solo no es física debido a la singularidad que ocurre en r=0; existen ondas viajeras hacia adentro.

Ver también

• Acústica
• atenuación acústica
• teoría acústica
• Ecuación de onda
• Ecuación de onda unidireccional
• Ecuaciones diferenciales
• Termodinámica
• Dinámica de fluidos
• Presión
• Ley de los gases ideales

Referencias

1. SP Näsholm y S. Holm, "Sobre una ecuación de onda elástica Zener fraccional", Fract. Calc. Aplica. Anal. vol. 16, No 1 (2013), págs. 26-50, DOI: 10.2478/s13540-013--0003-1 Enlace a e-print
2. Richard Feynman , Conferencias de física, volumen 1, capítulo 47: sonido. La ecuación de onda, Caltech 1963, 2006, 2013
3. Richard Feynman , Conferencias de física, volumen 1, 1969, Addison Publishing Company, Addison