Teoría de Debye-Hückel

Modelo que describe las desviaciones de la idealidad en soluciones de electrolitos y plasmas.

La teoría de Debye-Hückel fue propuesta por Peter Debye y Erich Hückel como una explicación teórica para las desviaciones de la idealidad en soluciones de electrolitos y plasmas . ^[1] Es un modelo de Poisson-Boltzmann linealizado , que supone un modelo extremadamente simplificado de solución de electrolito pero, sin embargo, dio predicciones precisas de los coeficientes de actividad media para iones en solución diluida. La ecuación de Debye-Hückel proporciona un punto de partida para los tratamientos modernos de la no idealidad de las soluciones de electrolitos. ^[2]

Descripción general

En la química de las soluciones electrolíticas , una solución ideal es una solución cuyas propiedades coligativas son proporcionales a la concentración del soluto . Las soluciones reales pueden mostrar desviaciones de este tipo de idealidad. Para dar cabida a estos efectos en la termodinámica de las soluciones, se introdujo el concepto de actividad : las propiedades son entonces proporcionales a las actividades de los iones. La actividad, a , es proporcional a la concentración, c . La constante de proporcionalidad se conoce como coeficiente de actividad , . ^[3] ${\displaystyle \gamma }$

${\displaystyle a=\gamma c/c^{0}}$

En una solución electrolítica ideal, los coeficientes de actividad de todos los iones son iguales a uno. La idealidad de una solución electrolítica solo se puede lograr en soluciones muy diluidas. La no idealidad de soluciones más concentradas surge principalmente (pero no exclusivamente) porque los iones de carga opuesta se atraen entre sí debido a fuerzas electrostáticas , mientras que los iones de la misma carga se repelen entre sí. En consecuencia, los iones no se distribuyen aleatoriamente en toda la solución, como lo estarían en una solución ideal.

Los coeficientes de actividad de iones individuales no se pueden medir experimentalmente porque una solución electrolítica debe contener iones con carga positiva y iones con carga negativa. En su lugar, se define un coeficiente de actividad medio. Por ejemplo, con el electrolito NaCl ${\displaystyle \gamma _{\pm }}$

${\displaystyle \gamma _{\pm }=\left(\gamma _{\mathrm {Na^{+}} }\gamma _{\mathrm {Cl^{-}} }\right)^{1/2}}$

En general, el coeficiente de actividad media de un electrolito completamente disociado de fórmula A _n B _m viene dado por ^[4]

${\displaystyle \gamma _{\pm }=\left({\gamma _{A}}^{n}{\gamma _{B}}^{m}\right)^{1/(n+m)}}$

Los coeficientes de actividad son en sí mismos funciones de la concentración, ya que la cantidad de interacción interiónica aumenta a medida que aumenta la concentración del electrolito. Debye y Hückel desarrollaron una teoría con la que se podían calcular los coeficientes de actividad de un solo ion. Al calcular los coeficientes de actividad promedio a partir de ellos, la teoría se podía probar con datos experimentales. Se descubrió que ofrecía una excelente concordancia para soluciones "diluidas".

El modelo

Una representación idealizada de una solución de un electrolito 1:1

Una descripción de la teoría de Debye-Hückel incluye un análisis muy detallado de los supuestos y sus limitaciones, así como del desarrollo matemático y sus aplicaciones. ^[5]

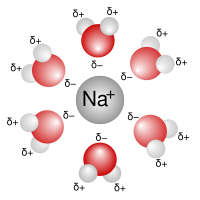
En la imagen se muestra una instantánea de una sección bidimensional de una solución electrolítica idealizada. Los iones se muestran como esferas con carga eléctrica unitaria. El disolvente (azul pálido) se muestra como un medio uniforme, sin estructura. En promedio, cada ion está rodeado más de cerca por iones de carga opuesta que por iones de carga similar. Estos conceptos se desarrollaron en una teoría cuantitativa que involucra iones de carga z ₁ e ⁺ y z ₂ e ⁻ , donde z puede ser cualquier número entero. La suposición principal es que la desviación de la idealidad se debe a interacciones electrostáticas entre iones, mediadas por la ley de Coulomb : la fuerza de interacción entre dos cargas eléctricas, separadas por una distancia, r en un medio de permitividad relativa ε _r está dada por ^[6]

${\displaystyle {\text{force}}={\frac {z_{1}z_{2}e^{2}}{4\pi \epsilon _{0}\epsilon _{r}r^{2}}}}$

También se supone que

• El soluto está completamente disociado; es un electrolito fuerte .
• Los iones son esféricos y no están polarizados por el campo eléctrico circundante . La solvatación de iones se ignora excepto en la medida en que determina los tamaños efectivos de los iones.
• El disolvente no juega ningún papel más que proporcionar un medio de permitividad relativa constante ( constante dieléctrica ).
• No hay electrostricción .
• Los iones individuales que rodean a un ion "central" pueden representarse mediante una nube de densidad de carga continua promediada estadísticamente, con una distancia mínima de aproximación más cercana.

El último supuesto significa que cada catión está rodeado por una nube esféricamente simétrica de otros iones. La nube tiene una carga neta negativa. De manera similar, cada anión está rodeado por una nube con carga neta positiva. ^[7]

Desarrollo matemático

La desviación de la idealidad se considera una función de la energía potencial resultante de las interacciones electrostáticas entre los iones y las nubes que los rodean. Para calcular esta energía se necesitan dos pasos.

El primer paso es especificar el potencial electrostático del ion j mediante la ecuación de Poisson.

${\displaystyle \nabla ^{2}\psi _{j}(r)=-{\frac {1}{\epsilon _{0}\epsilon _{r}}}\rho _{j}(r)}$

ψ( r ) es el potencial total a una distancia, r , del ion central y ρ( r ) es la densidad de carga promedio de la nube circundante a esa distancia. Para aplicar esta fórmula es esencial que la nube tenga simetría esférica, es decir, la densidad de carga es una función únicamente de la distancia al ion central ya que esto permite que la ecuación de Poisson se exprese en términos de coordenadas esféricas sin dependencia angular. ^[8]

El segundo paso es calcular la densidad de carga mediante una distribución de Boltzmann .

${\displaystyle n'_{i}=n_{i}\exp \left({\frac {-z_{i}e\psi _{j}(r)}{k_{\rm {B}}T}}\right)}$

donde k _B es la constante de Boltzmann y T es la temperatura. Esta distribución también depende del potencial ψ( r ) y esto introduce una dificultad seria en términos del principio de superposición . Sin embargo, las dos ecuaciones se pueden combinar para producir la ecuación de Poisson-Boltzmann . ^[9]

${\displaystyle \nabla ^{2}\psi _{j}(r)=-{\frac {1}{\epsilon _{0}\epsilon _{r}}}\sum _{i}\left\{n_{i}(z_{i}e)\exp \left({\frac {-z_{i}e\psi _{j}(r)}{k_{\rm {B}}T}}\right)\right\}}$

La solución de esta ecuación no es nada sencilla. Debye y Hückel desarrollaron la exponencial como una serie de Taylor truncada hasta el primer orden. El término de orden cero se anula porque la solución es, en promedio, eléctricamente neutra (de modo que Σ n _i z _i = 0), lo que nos deja solo con el término de primer orden. El resultado tiene la forma de la ecuación de Helmholtz ^[10]

${\displaystyle \nabla ^{2}\psi _{j}(r)=\kappa ^{2}\psi _{j}(r)\qquad {\text{with}}\qquad \kappa ^{2}={\frac {e^{2}}{\epsilon _{0}\epsilon _{r}k_{\rm {B}}T}}\sum _{i}n_{i}z_{i}^{2}}$,

que tiene una solución analítica . Esta ecuación se aplica a electrolitos con igual número de iones de cada carga. Los electrolitos no simétricos requieren otro término con ψ ² . Para electrolitos simétricos, esto se reduce a la ecuación esférica de Bessel modificada

${\displaystyle (\partial _{r}^{2}+{\frac {2}{r}}\partial _{r}-\kappa ^{2})\psi _{j}=0\qquad {\text{with solutions}}\qquad \psi _{j}(r)=A'{\frac {e^{-\kappa r}}{r}}+A''{\frac {e^{\kappa r}}{r}}}$

Los coeficientes y están fijados por las condiciones de contorno. Como , no debe divergir, entonces . En , que es la distancia del acercamiento más cercano de los iones, la fuerza ejercida por la carga debe ser equilibrada por la fuerza de otros iones, imponiendo , de la cual se encuentra, obteniéndose ${\displaystyle A'}$ ${\displaystyle A''}$ ${\displaystyle r\rightarrow \infty }$ ${\displaystyle \psi }$ ${\displaystyle A''=0}$ ${\displaystyle r=a_{0}}$ ${\displaystyle \partial _{r}\psi _{j}(a_{0})=-z_{j}e/(4\pi \epsilon _{0}\epsilon _{r}a_{0}^{2})}$ ${\displaystyle A'}$

${\displaystyle \psi _{j}(r)={\frac {z_{j}e}{4\pi \varepsilon _{0}\varepsilon _{r}}}{\frac {e^{\kappa a_{0}}}{1+\kappa a_{0}}}{\frac {e^{-\kappa r}}{r}}}$

La energía potencial electrostática , , del ion en es ${\displaystyle u_{j}}$ ${\displaystyle r=0}$

${\displaystyle u_{j}=z_{j}e{\Big (}\psi _{j}(a_{0})-{\frac {z_{j}e}{4\pi \varepsilon _{0}\varepsilon _{r}}}{\frac {1}{a_{0}}}{\Big )}=-{\frac {z_{j}^{2}e^{2}}{4\pi \varepsilon _{0}\varepsilon _{r}}}{\frac {\kappa }{1+\kappa a_{0}}}}$

Esta es la energía potencial de un solo ion en una solución. La generalización de carga múltiple de la electrostática proporciona una expresión para la energía potencial de toda la solución. El coeficiente de actividad media se obtiene mediante el logaritmo de esta cantidad, como se indica a continuación ^[11]

Valores experimentales para KBr a 25 °C (puntos) ^[12] y ley límite de Debye-Hückel (línea coloreada) ${\displaystyle \log \gamma _{\pm }}$

${\displaystyle \log _{10}\gamma _{\pm }=-Az_{j}^{2}{\frac {\sqrt {I}}{1+Ba_{0}{\sqrt {I}}}}}$

${\displaystyle A={\frac {e^{2}B}{2.303\times 8\pi \epsilon _{0}\epsilon _{r}k_{\rm {B}}T}}}$

${\displaystyle B=\left({\frac {2e^{2}N}{\epsilon _{0}\epsilon _{r}k_{\rm {B}}T}}\right)^{1/2}}$

donde I es la fuerza iónica y a ₀ es un parámetro que representa la distancia de aproximación más cercana de los iones. Para soluciones acuosas a 25 °C A = 0,51 mol ^−1/2 dm ^3/2 y B = 3,29 nm ⁻¹ mol ^−1/2 dm ^{3/2 [13]}

${\displaystyle A}$es una constante que depende de la temperatura. Si se expresa en términos de molalidad, en lugar de molaridad (como en la ecuación anterior y en el resto de este artículo), entonces un valor experimental para del agua es a 25 °C. Es común usar un logaritmo de base 10, en cuyo caso factorizamos , por lo que A es . El multiplicador anterior en la ecuación es para el caso en que las dimensiones de son . Cuando las dimensiones de son , el multiplicador debe eliminarse de la ecuación ^{[14] : sección 2.5.2} ${\displaystyle I}$ ${\displaystyle A}$ ${\displaystyle 1.172{\text{ mol}}^{-1/2}{\text{kg}}^{1/2}}$ ${\displaystyle \ln 10}$ ${\displaystyle 0.509{\text{ mol}}^{-1/2}{\text{kg}}^{1/2}}$ ${\displaystyle 10^{3}}$ ${\displaystyle I/2}$ ${\displaystyle I}$ ${\displaystyle {\text{mol}}/{\text{dm}}^{3}}$ ${\displaystyle I}$ ${\displaystyle {\text{mole}}/{\text{m}}^{3}}$ ${\displaystyle 10^{3}}$

El aspecto más significativo de este resultado es la predicción de que el coeficiente de actividad media es una función de la fuerza iónica en lugar de la concentración de electrolitos. Para valores muy bajos de la fuerza iónica, el valor del denominador en la expresión anterior se vuelve casi igual a uno. En esta situación, el coeficiente de actividad media es proporcional a la raíz cuadrada de la fuerza iónica. Esto se conoce como la ley límite de Debye-Hückel. En este límite, la ecuación se da de la siguiente manera ^{[14] : sección 2.5.2}

$${\displaystyle \ln(\gamma _{i})=-{\frac {z_{i}^{2}q^{2}\kappa }{8\pi \varepsilon _{r}\varepsilon _{0}k_{\text{B}}T}}=-{\frac {z_{i}^{2}q^{3}N_{\text{A}}^{1/2}}{4\pi (\varepsilon _{r}\varepsilon _{0}k_{\text{B}}T)^{3/2}}}{\sqrt {10^{3}{\frac {I}{2}}}}=-Az_{i}^{2}{\sqrt {I}},}$$

La presión osmótica en exceso obtenida a partir de la teoría de Debye-Hückel está en unidades cgs : ^[15] Por lo tanto, la presión total es la suma de la presión osmótica en exceso y la presión ideal . El coeficiente osmótico se expresa entonces mediante $${\displaystyle P^{\text{ex}}=-{\frac {k_{\text{B}}T\kappa _{\text{cgs}}^{3}}{24\pi }}=-{\frac {k_{\text{B}}T\left({\frac {4\pi \sum _{j}c_{j}q_{j}}{\varepsilon _{0}\varepsilon _{r}k_{\text{B}}T}}\right)^{3/2}}{24\pi }}.}$$ ${\textstyle P^{\text{id}}=k_{\text{B}}T\sum _{i}c_{i}}$ $${\displaystyle \phi ={\frac {P^{\text{id}}+P^{\text{ex}}}{P^{\text{id}}}}=1+{\frac {P^{\text{ex}}}{P^{\text{id}}}}.}$$

No dimensionalización

Tomando la ecuación diferencial de antes (como se dijo arriba, la ecuación sólo es válida para concentraciones bajas): $${\displaystyle {\frac {\partial ^{2}\varphi (r)}{\partial r^{2}}}+{\frac {2}{r}}{\frac {\partial \varphi (r)}{\partial r}}={\frac {Iq\varphi (r)}{\varepsilon _{r}\varepsilon _{0}k_{\text{B}}T}}=\kappa ^{2}\varphi (r).}$$

El uso del teorema π de Buckingham en este problema da como resultado los siguientes grupos adimensionales: se llama campo de potencial eléctrico escalar reducido. se llama radio reducido. Los grupos existentes pueden recombinarse para formar otros dos grupos adimensionales para la sustitución en la ecuación diferencial. El primero es lo que podría llamarse el cuadrado de la longitud de apantallamiento inversa reducida , . El segundo podría llamarse la carga iónica central reducida, (con Z mayúscula). Nótese que, aunque ya es adimensional, sin la sustitución dada a continuación, la ecuación diferencial seguiría siendo dimensional. $${\displaystyle {\begin{aligned}\pi _{1}&={\frac {q\varphi (r)}{k_{\text{B}}T}}=\Phi (R(r))\\\pi _{2}&=\varepsilon _{r}\\\pi _{3}&={\frac {ak_{\text{B}}T\varepsilon _{0}}{q^{2}}}\\\pi _{4}&=a^{3}I\\\pi _{5}&=z_{0}\\\pi _{6}&={\frac {r}{a}}=R(r).\end{aligned}}}$$ ${\displaystyle \Phi }$ ${\displaystyle R}$ ${\displaystyle (\kappa a)^{2}}$ ${\displaystyle Z_{0}}$ ${\displaystyle z_{0}}$

$${\displaystyle {\frac {\pi _{4}}{\pi _{2}\pi _{3}}}={\frac {a^{2}q^{2}I}{\varepsilon _{r}\varepsilon _{0}k_{\text{B}}T}}=(\kappa a)^{2}}$$ $${\displaystyle {\frac {\pi _{5}}{\pi _{2}\pi _{3}}}={\frac {z_{0}q^{2}}{4\pi a\varepsilon _{r}\varepsilon _{0}k_{\text{B}}T}}=Z_{0}}$$

Para obtener la ecuación diferencial no dimensionalizada y las condiciones iniciales, se utilizan los grupos para eliminar a favor de , luego eliminar a favor de mientras se lleva a cabo la regla de la cadena y se sustituye , luego eliminar a favor de (no se necesita regla de la cadena), luego eliminar a favor de , luego eliminar a favor de . Las ecuaciones resultantes son las siguientes: ${\displaystyle \pi }$ ${\displaystyle \varphi (r)}$ ${\displaystyle \Phi (R(r))}$ ${\displaystyle R(r)}$ ${\displaystyle r}$ ${\displaystyle {R^{\prime }}(r)=a}$ ${\displaystyle r}$ ${\displaystyle R}$ ${\displaystyle I}$ ${\displaystyle (\kappa a)^{2}}$ ${\displaystyle z_{0}}$ ${\displaystyle Z_{0}}$ $${\displaystyle {\frac {\partial \Phi (R)}{\partial R}}{\bigg |}_{R=1}=-Z_{0}}$$ $${\displaystyle \Phi (\infty )=0}$$ $${\displaystyle {\frac {\partial ^{2}\Phi (R)}{\partial R^{2}}}+{\frac {2}{R}}{\frac {\partial \Phi (R)}{\partial R}}=(\kappa a)^{2}\Phi (R).}$$

Para la sal de mesa en solución 0,01 M a 25 °C, un valor típico de es 0,0005636, mientras que un valor típico de es 7,017, lo que pone de relieve el hecho de que, en concentraciones bajas, es un objetivo para una aproximación de orden de magnitud cero, como el análisis de perturbaciones. Desafortunadamente, debido a la condición de contorno en el infinito, la perturbación regular no funciona. La misma condición de contorno nos impide encontrar la solución exacta de las ecuaciones. Sin embargo, la perturbación singular puede funcionar. ^{[ aclaración necesaria ] [ cita necesaria ]} ${\displaystyle (\kappa a)^{2}}$ ${\displaystyle Z_{0}}$ ${\displaystyle (\kappa a)^{2}}$

Limitaciones y extensiones

La primera capa de solvatación de un ion sodio disuelto en agua. Los átomos de oxígeno están dispuestos en los vértices de un octaedro con el ion sodio en su centro.

Esta ecuación concuerda satisfactoriamente con las mediciones experimentales para concentraciones bajas de electrolitos, típicamente menores a 10 ⁻³ mol/L. Las desviaciones de la teoría ocurren en concentraciones más altas y con electrolitos que producen iones de cargas más altas, particularmente electrolitos asimétricos. Esencialmente, estas desviaciones ocurren porque el modelo está demasiado simplificado , por lo que hay poco que ganar haciendo pequeños ajustes al modelo. ^[16] Las suposiciones individuales pueden ser cuestionadas a su vez. ${\displaystyle \log \gamma _{\pm }}$

• Disociación completa. Puede producirse asociación iónica , en particular con iones de mayor carga. Niels Bjerrum siguió este tema en detalle . La longitud de Bjerrum es la separación en la que la interacción electrostática entre dos iones es comparable en magnitud a kT .
• Electrolitos débiles. Un electrolito débil es aquel que no está completamente disociado. Como tal, tiene una constante de disociación . La constante de disociación se puede utilizar para calcular el grado de disociación y, por lo tanto, hacer la corrección necesaria para calcular los coeficientes de actividad. ^[17]
• Los iones son esféricos, no tienen cargas puntuales y no están polarizados . Muchos iones, como el ion nitrato , NO ₃ ⁻ , no son esféricos. Los iones poliatómicos también son polarizables.
• Papel del disolvente. El disolvente no es un medio sin estructura, sino que está formado por moléculas. Las moléculas de agua en solución acuosa son tanto dipolares como polarizables. Tanto los cationes como los aniones tienen una capa de solvatación primaria fuerte y una capa de solvatación secundaria más débil. Las interacciones ion-disolvente se ignoran en la teoría de Debye-Hückel.

Además, se supone que el radio iónico es insignificante, pero a concentraciones más altas, el radio iónico se vuelve comparable al radio de la atmósfera iónica . La mayoría de las extensiones de la teoría de Debye-Hückel son de naturaleza empírica. Por lo general, permiten seguir la ecuación de Debye-Hückel a baja concentración y agregan términos adicionales en alguna potencia de la fuerza iónica para ajustarse a las observaciones experimentales. Las principales extensiones son la ecuación de Davies , las ecuaciones de Pitzer y la teoría de interacción iónica específica .

Una de esas ecuaciones extendidas de Debye-Hückel viene dada por: donde su logaritmo común es el coeficiente de actividad, es la carga entera del ion (1 para H ⁺ , 2 para Mg ²⁺ etc.), es la fuerza iónica de la solución acuosa, y es el tamaño o diámetro efectivo del ion en angstroms . El radio hidratado efectivo del ion, a es el radio del ion y sus moléculas de agua estrechamente unidas. Los iones grandes y los iones menos cargados se unen al agua con menos fuerza y ​​tienen radios hidratados más pequeños que los iones más pequeños y más cargados. Los valores típicos son 3Å para iones como H ⁺ , Cl ⁻ , CN ⁻ y HCOO ⁻ . El diámetro efectivo para el ion hidronio es 9Å. y son constantes con valores de respectivamente 0,5085 y 0,3281 a 25 °C en agua ^[1] . $${\displaystyle -\log _{10}(\gamma )={\frac {A|z_{+}z_{-}|{\sqrt {I}}}{1+Ba{\sqrt {I}}}}}$$ ${\displaystyle \gamma }$ ${\displaystyle z}$ ${\displaystyle I}$ ${\displaystyle a}$ ${\displaystyle A}$ ${\displaystyle B}$

La ecuación de Debye-Hückel extendida proporciona resultados precisos para μ ≤ 0,1. Para soluciones con fuerzas iónicas mayores, se deben utilizar las ecuaciones de Pitzer . En estas soluciones, el coeficiente de actividad puede aumentar con la fuerza iónica.

Diagrama de Debye-Hückel con diferentes valores para la carga iónica Z y el diámetro iónico a

La ecuación de Debye-Hückel no se puede utilizar en soluciones de surfactantes donde la presencia de micelas influye en las propiedades electroquímicas del sistema (incluso un juicio aproximado sobreestima γ en un ~50%).

Mezclas de electrolitos

La teoría también se puede aplicar a soluciones diluidas de electrolitos mixtos. Para este fin se han utilizado mediciones de la depresión del punto de congelación . ^[18]

Conductividad

Fuerzas que afectan a un ion o nube cargada que se mueve en un campo eléctrico

El tratamiento dado hasta ahora es para un sistema no sujeto a un campo eléctrico externo. Cuando se mide la conductividad , el sistema está sujeto a un campo externo oscilante debido a la aplicación de un voltaje de CA a electrodos sumergidos en la solución. Debye y Hückel modificaron su teoría en 1926 y su teoría fue modificada nuevamente por Lars Onsager en 1927. Se conservaron todos los postulados de la teoría original. Además, se asumió que el campo eléctrico hace que la nube de carga se distorsione lejos de la simetría esférica. ^[19] Después de tomar esto en cuenta, junto con los requisitos específicos de los iones en movimiento, como la viscosidad y los efectos electroforéticos , Onsager pudo derivar una expresión teórica para explicar la relación empírica conocida como Ley de Kohlrausch , para la conductividad molar, Λ _m .

${\displaystyle \Lambda _{m}=\Lambda _{m}^{0}-K{\sqrt {c}}}$

${\displaystyle \Lambda _{m}^{0}}$se conoce como conductividad molar límite, K es una constante empírica y c es la concentración de electrolito. Límite aquí significa "en el límite de la dilución infinita"). La expresión de Onsager es

${\displaystyle \Lambda _{m}=\Lambda _{m}^{0}-(A+B\Lambda _{m}^{0}){\sqrt {c}}}$

donde A y B son constantes que dependen únicamente de magnitudes conocidas como la temperatura, las cargas de los iones y la constante dieléctrica y la viscosidad del disolvente. Esta ecuación se conoce como ecuación de Debye-Hückel-Onsager. Sin embargo, esta ecuación sólo se aplica a soluciones muy diluidas y ha sido reemplazada en gran medida por otras ecuaciones debido a Fuoss y Onsager, 1932 y 1957 y posteriores. ^[20]

Resumen del primer artículo de Debye y Hückel sobre la teoría de los electrolitos diluidos

El título en inglés del artículo es "On the Theory of Electrolytes. I. Freezing Point Depression and Related Phenomena". Fue publicado originalmente en 1923 en el volumen 24 de una revista en idioma alemán Physikalische Zeitschrift . Una traducción al inglés ^{[21] : 217–63} del artículo está incluida en un libro de artículos recopilados presentados a Debye por "sus alumnos, amigos y los editores con motivo de su septuagésimo cumpleaños el 24 de marzo de 1954". ^{[21] : xv} Otra traducción al inglés se completó en 2019. ^[22] El artículo trata sobre el cálculo de las propiedades de las soluciones de electrolitos que están bajo la influencia de campos eléctricos inducidos por iones, por lo que trata sobre electrostática .

En el mismo año en que publicaron por primera vez este artículo, Debye y Hückel, en adelante D&H, también publicaron un artículo que cubría su caracterización inicial de soluciones bajo la influencia de campos eléctricos llamado "Sobre la teoría de electrolitos. II. Ley límite para la conductividad eléctrica", pero ese artículo posterior no está (todavía) cubierto aquí.

En el siguiente resumen (aún incompleto y sin revisar) se utilizan notaciones y terminología modernas, tanto de la química como de las matemáticas, para evitar confusiones. Además, con algunas excepciones para mejorar la claridad, las subsecciones de este resumen son versiones (muy) condensadas de las mismas subsecciones del artículo original.

Introducción

D&H observan que la fórmula de Guldberg-Waage para especies de electrolitos en equilibrio de reacción química en forma clásica es ^{[21] : 221} donde $${\displaystyle \prod _{i=1}^{s}x_{i}^{\nu _{i}}=K,}$$

• ${\textstyle \prod }$es una notación para la multiplicación ,
• ${\displaystyle i}$es una variable ficticia que indica la especie,
• ${\displaystyle s}$es el número de especies que participan en la reacción,
• ${\displaystyle x_{i}}$es la fracción molar de la especie , ${\displaystyle i}$
• ${\displaystyle \nu _{i}}$es el coeficiente estequiométrico de las especies , ${\displaystyle i}$
• K es la constante de equilibrio .

D&H dicen que, debido a las "fuerzas electrostáticas mutuas entre los iones", es necesario modificar la ecuación de Guldberg-Waage reemplazándola por , donde es un coeficiente de actividad general, no un coeficiente de actividad "especial" (un coeficiente de actividad separado asociado con cada especie), que es lo que se utiliza en la química moderna a partir de 2007 . ${\displaystyle K}$ ${\displaystyle \gamma K}$ ${\displaystyle \gamma }$^[update]

La relación entre y los coeficientes de actividad especial es ^{[21] : 248} ${\displaystyle \gamma }$ ${\displaystyle \gamma _{i}}$ $${\displaystyle \log(\gamma )=\sum _{i=1}^{s}\nu _{i}\log(\gamma _{i}).}$$

Fundamentos

D&H utiliza las entropías libres de Helmholtz y Gibbs para expresar el efecto de las fuerzas electrostáticas en un electrolito sobre su estado termodinámico. En concreto, dividen la mayoría de los potenciales termodinámicos en términos clásicos y electrostáticos: donde ${\displaystyle \Phi }$ ${\displaystyle \Xi }$ $${\displaystyle \Phi =S-{\frac {U}{T}}=-{\frac {A}{T}},}$$

• ${\displaystyle \Phi }$¿ Es la entropía libre de Helmholtz ?
• ${\displaystyle S}$es entropía ,
• ${\displaystyle U}$es energía interna ,
• ${\displaystyle T}$es la temperatura ,
• ${\displaystyle A}$¿Es energía libre de Helmholtz ?

D&H dan el diferencial total de como ^{[21] : 222} donde ${\displaystyle \Phi }$ $${\displaystyle d\Phi ={\frac {P}{T}}\,dV+{\frac {U}{T^{2}}}\,dT,}$$

• ${\displaystyle P}$es presión ,
• ${\displaystyle V}$es volumen​

Por la definición del diferencial total, esto significa aquello que es útil más adelante. $${\displaystyle {\frac {P}{T}}={\frac {\partial \Phi }{\partial V}},}$$ $${\displaystyle {\frac {U}{T^{2}}}={\frac {\partial \Phi }{\partial T}},}$$

Como se dijo anteriormente, la energía interna se divide en dos partes: ^{[21] : 222} donde $${\displaystyle U=U_{k}+U_{e}}$$

• ${\displaystyle k}$indica la parte clásica,
• ${\displaystyle e}$Indica la parte eléctrica.

De manera similar, la entropía libre de Helmholtz también se divide en dos partes: $${\displaystyle \Phi =\Phi _{k}+\Phi _{e}.}$$

D&H afirman, sin dar la lógica, que ^{[21] : 222} $${\displaystyle \Phi _{e}=\int {\frac {U_{e}}{T^{2}}}\,dT.}$$

Pareciera que, sin justificación alguna, $${\displaystyle \Phi _{e}=\int {\frac {P_{e}}{T}}\,dV+\int {\frac {U_{e}}{T^{2}}}\,dT.}$$

Sin mencionarlo específicamente, D&H luego dan lo que podría ser la justificación requerida (arriba) al argumentar que , una suposición de que el solvente es incompresible. ${\displaystyle \Phi _{e}=\Xi _{e}}$

La definición de la entropía libre de Gibbs es ^{[21] : 222–3} donde es la energía libre de Gibbs . ${\displaystyle \Xi }$ $${\displaystyle \Xi =S-{\frac {U+PV}{T}}=\Phi -{\frac {PV}{T}}=-{\frac {G}{T}},}$$ ${\displaystyle G}$

D&H dan el diferencial total de como ^{[21] : 222} ${\displaystyle \Xi }$ $${\displaystyle d\Xi =-{\frac {V}{T}}\,dP+{\frac {U+PV}{T^{2}}}\,dT.}$$

En este punto, D&H observan que, para agua que contiene 1 mol por litro de cloruro de potasio (no se dan la presión nominal ni la temperatura), la presión eléctrica asciende a 20 atmósferas. Además, observan que este nivel de presión da un cambio de volumen relativo de 0,001. Por lo tanto, descuidan el cambio en el volumen del agua debido a la presión eléctrica, escribiendo ^{[21] : 223} y colocando ${\displaystyle P_{e}}$ $${\displaystyle \Xi =\Xi _{k}+\Xi _{e},}$$ $${\displaystyle \Xi _{e}=\Phi _{e}=\int {\frac {U_{e}}{T^{2}}}\,dT.}$$

D&H dicen que, según Planck, la parte clásica de la entropía libre de Gibbs es ^{[21] : 223} donde $${\displaystyle \Xi _{k}=\sum _{i=0}^{s}N_{i}(\xi _{i}-k_{\text{B}}ln(x_{i})),}$$

• ${\displaystyle i}$es una especie,
• ${\displaystyle s}$es el número de diferentes tipos de partículas en solución,
• ${\displaystyle N_{i}}$es el número de partículas de la especie i ,
• ${\displaystyle \xi _{i}}$es la entropía libre de Gibbs específica de la partícula de la especie i ,
• ${\displaystyle k_{\text{B}}}$es la constante de Boltzmann ,
• ${\displaystyle x_{i}}$es la fracción molar de la especie i .

La especie cero es el disolvente. La definición de es la siguiente, donde las letras minúsculas indican las versiones específicas de la partícula de las propiedades extensivas correspondientes: ^{[21] : 223} ${\displaystyle \xi _{i}}$ $${\displaystyle \xi _{i}=s_{i}-{\frac {u_{i}+Pv_{i}}{T}}.}$$

D&H no lo dice, pero la forma funcional puede derivarse de la dependencia funcional del potencial químico de un componente de una mezcla ideal respecto de su fracción molar. ^[23] ${\displaystyle \Xi _{k}}$

D&H observan que la energía interna de una solución se reduce por la interacción eléctrica de sus iones, pero que este efecto no se puede determinar utilizando la aproximación cristalográfica para las distancias entre átomos diferentes (la raíz cúbica de la relación entre el volumen total y el número de partículas en el volumen). Esto se debe a que hay más movimiento térmico en una solución líquida que en un cristal. El movimiento térmico tiende a difuminar la red natural que de otro modo construirían los iones. En cambio, D&H introducen el concepto de atmósfera o nube iónica . Al igual que la red cristalina, cada ion todavía intenta rodearse de iones de carga opuesta, pero de una manera más libre; a pequeñas distancias de los iones positivos, es más probable encontrar iones negativos y viceversa. ^{[21] : 225} ${\displaystyle U}$

La energía potencial de una solución iónica arbitraria

La electroneutralidad de una solución requiere que ^{[21] : 233} donde $${\displaystyle \sum _{i=1}^{s}N_{i}z_{i}=0,}$$

• ${\displaystyle N_{i}}$es el número total de iones de la especie i en la solución,
• ${\displaystyle z_{i}}$es el número de carga de la especie i .

Para llevar un ion de especie i , inicialmente lejano, a un punto dentro de la nube de iones se requiere una energía de interacción en la cantidad de , donde es la carga elemental , y es el valor del campo de potencial eléctrico escalar en . Si las fuerzas eléctricas fueran el único factor en juego, la configuración de energía mínima de todos los iones se lograría en una configuración reticular compacta. Sin embargo, los iones están en equilibrio térmico entre sí y son relativamente libres de moverse. Por lo tanto, obedecen las estadísticas de Boltzmann y forman una distribución de Boltzmann . Las densidades numéricas de todas las especies se alteran de sus valores volumétricos (promedio general) por el factor de Boltzmann correspondiente , donde es la constante de Boltzmann , y es la temperatura. ^[24] Por lo tanto, en cada punto de la nube ^{[21] : 233} ${\displaystyle P}$ ${\displaystyle z_{i}q\varphi }$ ${\displaystyle q}$ ${\displaystyle \varphi }$ ${\displaystyle P}$ ${\displaystyle n_{i}}$ ${\displaystyle n_{i}^{0}}$ ${\displaystyle e^{-{\frac {z_{i}q\varphi }{k_{\text{B}}T}}}}$ ${\displaystyle k_{\text{B}}}$ ${\displaystyle T}$ $${\displaystyle n_{i}={\frac {N_{i}}{V}}e^{-{\frac {z_{i}q\varphi }{k_{\text{B}}T}}}=n_{i}^{0}e^{-{\frac {z_{i}q\varphi }{k_{\text{B}}T}}}.}$$

Obsérvese que en el límite de temperatura infinito, todos los iones se distribuyen uniformemente, sin tener en cuenta sus interacciones electrostáticas. ^{[21] : 227}

La densidad de carga está relacionada con la densidad numérica: ^{[21] : 233} $${\displaystyle \rho =\sum _{i}z_{i}qn_{i}=\sum _{i}z_{i}qn_{i}^{0}e^{-{\frac {z_{i}q\varphi }{k_{\text{B}}T}}}.}$$

Al combinar este resultado para la densidad de carga con la ecuación de Poisson de la electrostática, resulta una forma de la ecuación de Poisson-Boltzmann : ^{[21] : 233} $${\displaystyle \nabla ^{2}\varphi =-{\frac {\rho }{\varepsilon _{r}\varepsilon _{0}}}=-\sum _{i}{\frac {z_{i}qn_{i}^{0}}{\varepsilon _{r}\varepsilon _{0}}}e^{-{\frac {z_{i}q\varphi }{k_{\text{B}}T}}}.}$$

Esta ecuación es difícil de resolver y no sigue el principio de superposición lineal para la relación entre el número de cargas y la intensidad del campo de potencial. Fue resuelta analíticamente por el matemático sueco Thomas Hakon Gronwall y sus colaboradores, los físico-químicos VK La Mer y Karl Sandved, en un artículo de 1928 de la revista Physikalische Zeitschrift que trataba sobre las extensiones de la teoría de Debye-Huckel. ^[25]

Sin embargo, para concentraciones suficientemente bajas de iones, se puede utilizar una aproximación de expansión de la serie de Taylor de primer orden para la función exponencial ( para ) para crear una ecuación diferencial lineal. ^{[14] : Sección 2.4.2} D&H dicen que esta aproximación se cumple a grandes distancias entre iones, ^{[21] : 227} lo que es lo mismo que decir que la concentración es baja. Por último, afirman sin prueba que la adición de más términos en la expansión tiene poco efecto en la solución final. ^{[21] : 227} Por lo tanto ${\displaystyle e^{x}\approx 1+x}$ ${\displaystyle 0<x\ll 1}$ $${\displaystyle -\sum _{i}{\frac {z_{i}qn_{i}^{0}}{\varepsilon _{r}\varepsilon _{0}}}e^{-{\frac {z_{i}q\varphi }{k_{\text{B}}T}}}\approx -\sum _{i}{\frac {z_{i}qn_{i}^{0}}{\varepsilon _{r}\varepsilon _{0}}}\left(1-{\frac {z_{i}q\varphi }{k_{\text{B}}T}}\right)=-\left(\sum _{i}{\frac {z_{i}qn_{i}^{0}}{\varepsilon _{r}\varepsilon _{0}}}-\sum _{i}{\frac {z_{i}^{2}q^{2}n_{i}^{0}\varphi }{\varepsilon _{r}\varepsilon _{0}k_{\text{B}}T}}\right).}$$

La ecuación de Poisson-Boltzmann se transforma en ^{[21] : 233} porque la primera suma es cero debido a la electroneutralidad. ^{[21] : 234} $${\displaystyle \nabla ^{2}\varphi =\sum _{i}{\frac {z_{i}^{2}q^{2}n_{i}^{0}\varphi }{\varepsilon _{r}\varepsilon _{0}k_{\text{B}}T}},}$$

Factorizamos el potencial escalar y asignamos los sobrantes, que son constantes, a . Además, sea la fuerza iónica de la solución: ^{[21] : 234} ${\displaystyle \kappa ^{2}}$ ${\displaystyle I}$ $${\displaystyle \kappa ^{2}=\sum _{i}{\frac {z_{i}^{2}q^{2}n_{i}^{0}}{\varepsilon _{r}\varepsilon _{0}k_{\text{B}}T}}={\frac {2Iq^{2}}{\varepsilon _{r}\varepsilon _{0}k_{\text{B}}T}},}$$ $${\displaystyle I={\frac {1}{2}}\sum _{i}z_{i}^{2}n_{i}^{0}.}$$

Así, la ecuación fundamental se reduce a una forma de la ecuación de Helmholtz : ^[26] $${\displaystyle \nabla ^{2}\varphi =\kappa ^{2}\varphi .}$$

Hoy en día, se denomina longitud de cribado de Debye . D&H reconoce la importancia del parámetro en su artículo y lo caracteriza como una medida del espesor de la atmósfera iónica, que es una doble capa eléctrica del tipo Gouy-Chapman. ^{[21] : 229} ${\displaystyle \kappa ^{-1}}$

La ecuación puede expresarse en coordenadas esféricas tomando un ion arbitrario: ^{[27] [21] : 229} ${\displaystyle r=0}$ $${\displaystyle \nabla ^{2}\varphi ={\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}\left(r^{2}{\frac {\partial \varphi (r)}{\partial r}}\right)={\frac {\partial ^{2}\varphi (r)}{\partial r^{2}}}+{\frac {2}{r}}{\frac {\partial \varphi (r)}{\partial r}}=\kappa ^{2}\varphi (r).}$$

La ecuación tiene la siguiente solución general (tenga en cuenta que es una constante positiva): ^{[21] : 229} donde , , y son constantes indeterminadas ${\displaystyle \kappa }$ $${\displaystyle \varphi (r)=A{\frac {e^{-{\sqrt {\kappa ^{2}}}r}}{r}}+A'{\frac {e^{{\sqrt {\kappa ^{2}}}r}}{2r{\sqrt {\kappa ^{2}}}}}=A{\frac {e^{-\kappa r}}{r}}+A''{\frac {e^{\kappa r}}{r}}=A{\frac {e^{-\kappa r}}{r}},}$$ ${\displaystyle A}$ ${\displaystyle A'}$ ${\displaystyle A''}$

El potencial eléctrico es cero en el infinito por definición, por lo que debe ser cero. ^{[21] : 229} ${\displaystyle A''}$

En el siguiente paso, D&H suponen que existe un cierto radio , más allá del cual ningún ion en la atmósfera puede acercarse al centro (de carga) del ion aislado. Este radio puede deberse al tamaño físico del ion en sí, a los tamaños de los iones en la nube y a cualquier molécula de agua que rodee a los iones. Matemáticamente, tratan al ion aislado como una carga puntual a la que uno no puede acercarse dentro del radio . ^{[21] : 231} ${\displaystyle a_{i}}$ ${\displaystyle a_{i}}$

El potencial de una carga puntual por sí mismo es $${\displaystyle \varphi _{\text{pc}}(r)={\frac {1}{4\pi \varepsilon _{r}\varepsilon _{0}}}{\frac {z_{i}q}{r}}.}$$

D&H dicen que el potencial total dentro de la esfera es ^{[21] : 232} donde es una constante que representa el potencial añadido por la atmósfera iónica. No se da ninguna justificación para ser una constante. Sin embargo, se puede ver que este es el caso considerando que cualquier distribución de carga estática esférica está sujeta a las matemáticas del teorema de capas . El teorema de capas dice que no se ejerce ninguna fuerza sobre partículas cargadas dentro de una esfera (de carga arbitraria). ^[28] Dado que se supone que la atmósfera iónica es (promediada en el tiempo) esféricamente simétrica, con una carga que varía en función del radio , puede representarse como una serie infinita de capas de carga concéntricas. Por lo tanto, dentro del radio , la atmósfera iónica no ejerce ninguna fuerza. Si la fuerza es cero, entonces el potencial es una constante (por definición). $${\displaystyle \varphi _{\text{sp}}(r)=\varphi _{\text{pc}}(r)+B_{i}={\frac {1}{4\pi \varepsilon _{r}\varepsilon _{0}}}{\frac {z_{i}q}{r}}+B_{i},}$$ ${\displaystyle B_{i}}$ ${\displaystyle B_{i}}$ ${\displaystyle r}$ ${\displaystyle a_{i}}$

En una combinación del modelo de distribución continua que dio la ecuación de Poisson-Boltzmann y el modelo de la carga puntual, se supone que en el radio , hay una continuidad de y su primera derivada. Por lo tanto ^{[21] : 232} ${\displaystyle a_{i}}$ ${\displaystyle \varphi (r)}$ $${\displaystyle \varphi (a_{i})=A_{i}{\frac {e^{-\kappa a_{i}}}{a_{i}}}={\frac {1}{4\pi \varepsilon _{r}\varepsilon _{0}}}{\frac {z_{i}q}{a_{i}}}+B_{i}=\varphi _{\text{sp}}(a_{i}),}$$ $${\displaystyle \varphi '(a_{i})=-{\frac {A_{i}e^{-\kappa a_{i}}(1+\kappa a_{i})}{a_{i}^{2}}}=-{\frac {1}{4\pi \varepsilon _{r}\varepsilon _{0}}}{\frac {z_{i}q}{a_{i}^{2}}}=\varphi _{\text{sp}}'(a_{i}),}$$ $${\displaystyle A_{i}={\frac {z_{i}q}{4\pi \varepsilon _{r}\varepsilon _{0}}}{\frac {e^{\kappa a_{i}}}{1+\kappa a_{i}}},}$$ $${\displaystyle B_{i}=-{\frac {z_{i}q\kappa }{4\pi \varepsilon _{r}\varepsilon _{0}}}{\frac {1}{1+\kappa a_{i}}}.}$$

Según la definición de energía potencial eléctrica , la energía potencial asociada con el ion aislado en la atmósfera iónica es ^{[21] : 230 y 232} $${\displaystyle u_{i}=z_{i}qB_{i}=-{\frac {z_{i}^{2}q^{2}\kappa }{4\pi \varepsilon _{r}\varepsilon _{0}}}{\frac {1}{1+\kappa a_{i}}}.}$$

Tenga en cuenta que esto solo requiere el conocimiento de la carga del ion seleccionado y el potencial de todos los demás iones.

Para calcular la energía potencial de toda la solución electrolítica, se debe utilizar la generalización de carga múltiple para la energía potencial eléctrica: ^{[21] : 230 y 232} $${\displaystyle U_{e}={\frac {1}{2}}\sum _{i=1}^{s}N_{i}u_{i}=-\sum _{i=1}^{s}{\frac {N_{i}z_{i}^{2}}{2}}{\frac {q^{2}\kappa }{4\pi \varepsilon _{r}\varepsilon _{0}}}{\frac {1}{1+\kappa a_{i}}}.}$$

El término eléctrico adicional al potencial termodinámico

Verificación experimental de la teoría

Para verificar la validez de la teoría de Debye-Hückel se han probado muchas formas experimentales, midiendo los coeficientes de actividad: el problema es que necesitamos llegar a diluciones muy altas. Ejemplos típicos son: mediciones de presión de vapor, punto de congelación, presión osmótica (métodos indirectos) y medición del potencial eléctrico en las células (método directo). Yendo hacia diluciones altas se han encontrado buenos resultados usando células de membrana líquida, ha sido posible investigar medios acuosos 10 ⁻⁴ M y se ha encontrado que para electrolitos 1:1 (como NaCl o KCl) la ecuación de Debye-Hückel es totalmente correcta, pero para electrolitos 2:2 o 3:2 es posible encontrar desviación negativa de la ley límite de Debye-Hückel: este extraño comportamiento puede observarse solo en el área muy diluida, y en regiones más concentradas la desviación se vuelve positiva. Es posible que la ecuación de Debye–Hückel no sea capaz de prever este comportamiento debido a la linealización de la ecuación de Poisson–Boltzmann, o tal vez no: los estudios sobre esto se iniciaron solo durante los últimos años del siglo XX porque antes no era posible investigar la región de 10 ⁻⁴ M, por lo que es posible que durante los próximos años nazcan nuevas teorías.

Véase también

• Electrólito
• Actividad química
• Fuerza iónica
• Ecuación de Poisson-Boltzmann
• Longitud de Debye
• Longitud de Bjerrum
• Convención Bates-Guggenheim
• Atmósfera jónica
• Doble capa eléctrica
• Asociación de iones
• Ecuación de Davies
• Ecuación de Pitzer
• Teoría de la interacción iónica específica

Referencias

1. P. Debye y E. Hückel (1923). "Zur Theorie der Elektrolyte. I. Gefrierpunktserniedrigung und verwandte Erscheinungen". Physikalische Zeitschrift . 24 : 185-206.
2. Wright, MR (2007). Introducción a las soluciones electrolíticas acuosas . Wiley. ISBN 978-0-470-84293-5.
3. Wright, sección 1.10
4. Wright, Sección 8.23
5. Wright, capítulo 10.
6. Wright, Sección 10.3
7. Wright, Sección 10.3
8. Wright, sección 10.6.3
9. Wright, sección 10.6.8
10. Wright, sección 10.6.10
11. Wright, sección 10.6.15
12. Datos de Wright, Problema resuelto 8.17
13. Wright, sección 10.7
14. Hamann, Hamnett y Vielstich (1998). Electroquímica . Weinheim: Wiley-VCH Verlag GmbH. ISBN 3-527-29096-6.{{cite book}}: CS1 maint: multiple names: authors list (link)
15. http://homepages.rpi.edu/~keblip/THERMO/chapters/Chapter33.pdf, página 9.
16. Wright, sección 10.9.
17. Davies, CW (1962). Ion Association . Londres: Butterworths. págs. 37–53.
18. R. Wasoe, Física , 30 (1929), 412
19. Wright, sección 12.3
20. Wright, secciones 12.10 a 12.17
21. Los documentos recopilados de Peter JW Debye . Nueva York, Nueva York: Interscience Publishers, Inc. 1954.
22. P. Debye y E. Hückel (1923). "Zur Theorie der Elektrolyte. I. Gefrierpunktserniedrigung und verwandte Erscheinungen". Physikalische Zeitschrift . 24 : 185-206.
23. Salzman, William R. (21 de agosto de 2001). «Mezclas; cantidades molares parciales; soluciones ideales». Termodinámica química . Universidad de Arizona. Archivado desde el original el 7 de junio de 2007. Consultado el 23 de octubre de 2007 .
24. http://www.pma.caltech.edu/Courses/ph136/yr2006/text.html Archivado el 28 de agosto de 2007 en Wayback Machine , sección 19.3
25. Hille, Einar (1932). "Thomas Hakon Gronwall—In memoriam". Bull. Amer. Math. Soc . 38 (11): 775–786. doi : 10.1090/s0002-9904-1932-05492-1 . MR  1562506.
26. http://guava.physics.uiuc.edu/~nigel/courses/569/Essays_2004/files/lu.pdf sección 3.1)
27. "Ecuaciones de LaPlace y Poisson".
28. "Potencial eléctrico de una esfera cargada".