Problema con el Jeep

Problema matemático de colocación de depósitos de combustible

Gráfico de la cantidad de combustible f vs la distancia desde el origen d para explorar (1–3) y cruzar (I–III) versiones del problema del jeep para tres unidades de combustible: las flechas de colores indican depósitos, los segmentos diagonales indican viaje y los segmentos verticales indican transferencia de combustible

El problema del jeep , ^[1] el problema de cruzar el desierto ^[2] o el problema de exploración ^[3] es un problema matemático en el que un jeep debe maximizar la distancia que puede recorrer en un desierto con una cantidad dada de combustible. El jeep solo puede llevar una cantidad fija y limitada de combustible, pero puede dejar combustible y recolectarlo en depósitos de combustible en cualquier lugar del desierto.

El problema apareció por primera vez en la colección del siglo IX Propositiones ad Acuendos Juvenes ( Problemas para agudizar a los jóvenes ), atribuida a Alcuino , y trataba sobre un camello viajero que comía grano. ^[4] El De viribus quantitatis (c. 1500) de Luca Pacioli también analiza el problema. NJ Fine le dio un tratamiento moderno en 1947. ^[1]

Problema

Gráfico a escala de las versiones de exploración (arriba) y cruce (abajo) del problema del jeep para tres unidades de combustible. El eje horizontal indica la distancia y el eje vertical indica el tiempo. Los segmentos de línea verticales de color indican el combustible almacenado y los horizontales indican el viaje utilizando el combustible extraído. Los números de color indican las unidades de combustible almacenadas en ese momento.

Hay n unidades de combustible almacenadas en una base fija. El jeep puede transportar como máximo 1 unidad de combustible en cualquier momento y puede recorrer 1 unidad de distancia con 1 unidad de combustible (se supone que el consumo de combustible del jeep es constante). En cualquier momento de un viaje, el jeep puede dejar cualquier cantidad de combustible que lleve en un depósito de combustible o puede recoger cualquier cantidad de combustible que haya quedado en un depósito de combustible en un viaje anterior, siempre que su carga de combustible nunca supere 1 unidad. Hay dos variantes del problema:

• Explorando el desierto  : el jeep debe regresar a la base al final de cada viaje.
• Cruzando el desierto  – el jeep debe regresar a la base al final de cada viaje, excepto en el viaje final, cuando el jeep viaja lo más lejos que puede antes de quedarse sin combustible.

En cualquier caso, el objetivo es maximizar la distancia recorrida por el jeep en su viaje final. Alternativamente, el objetivo puede ser encontrar la menor cantidad de combustible necesaria para realizar un viaje final de una distancia determinada.

Variaciones

En el problema clásico, el combustible en el jeep y en los depósitos de combustible se considera una cantidad continua . Se han propuesto variaciones más complejas del problema en las que el combustible solo puede dejarse o recogerse en cantidades discretas. ^[5]

Solución

Solución a la variante "explorar el desierto" para n  = 3, que muestra el contenido de combustible del jeep y los depósitos de combustible al inicio de cada viaje y en el punto de retorno de cada viaje.

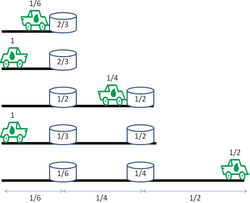
Una estrategia que maximiza la distancia recorrida en el viaje final para la variante “explorar el desierto” es la siguiente:

• El jeep hace n viajes. En cada viaje parte de la base con 1 unidad de combustible.
• En el primer viaje, el jeep recorre una distancia de 1/(2 n ) unidades y deja ( n  − 1)/ n unidades de combustible en un depósito de combustible. El jeep todavía tiene 1/(2 n ) unidades de combustible, lo suficiente para regresar a la base.
• En cada uno de los n  − 1 viajes subsiguientes, el jeep recoge 1/(2 n ) unidades de combustible de este primer depósito de combustible en el camino de ida, de modo que sale del depósito de combustible con 1 unidad de combustible. También recoge 1/(2 n ) unidades de combustible de este primer depósito de combustible en el camino de vuelta, que es justo el combustible suficiente para regresar a la base.
• En el segundo viaje, el jeep se desplaza hasta el primer depósito de combustible y se reabastece. Luego recorre una distancia de 1/(2 n  − 2) unidades y deja ( n  − 2)/( n  − 1) unidades de combustible en un segundo depósito de combustible. El jeep todavía tiene 1/(2 n  − 2) unidades de combustible, que es justo lo suficiente para regresar al primer depósito de combustible. Aquí recoge 1/(2 n ) unidades de combustible, que es justo lo suficiente para regresar a la base.
• En cada uno de los n  − 2 viajes subsiguientes, el jeep recoge 1/(2 n  − 2) unidades de combustible de este segundo depósito de combustible en el camino de ida, de modo que sale del depósito de combustible con 1 unidad de combustible. También recoge 1/(2 n  − 2) unidades de combustible del segundo depósito de combustible en el camino de regreso, que es justo el combustible suficiente para regresar al primer depósito de combustible.
• El jeep continúa de esta manera, de modo que en el viaje k establece un nuevo k -ésimo depósito de combustible a una distancia de 1/(2 n  − 2 k  + 2) unidades del depósito de combustible anterior y deja allí ( n  −  k )/( n  −  k  + 1) unidades de combustible. En cada uno de los n  −  k viajes posteriores recoge 1/(2 n  − 2 k  + 2) unidades de combustible del k -ésimo depósito a su ida y otras 1/(2 n  − 2 k  + 2) unidades de combustible a su vuelta.

Cuando el jeep inicia su viaje final, hay n  − 1 depósitos de combustible. El más lejano contiene 1/2 unidad de combustible, el siguiente más lejano contiene 1/3 de unidad de combustible, y así sucesivamente, y el depósito de combustible más cercano tiene solo 1/ n unidades de combustible restantes. Junto con 1 unidad de combustible con la que comienza desde la base, esto significa que el jeep puede recorrer una distancia total de ida y vuelta de

${\displaystyle 1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots +{\frac {1}{n}}=\sum _{k=1}^{n}{\frac {1}{k}}\equiv 2\times \mathrm {explore} (n)}$

unidades en su viaje final (la distancia máxima recorrida en el desierto es la mitad de esto). ^[3] Recoge la mitad del combustible restante en cada depósito de combustible en el camino de ida, lo que llena su tanque. Después de dejar el depósito de combustible más lejano, viaja 1/2 unidad más adentro del desierto y luego regresa al depósito de combustible más lejano. Recoge el combustible restante de cada depósito de combustible en el camino de regreso, que es suficiente para llegar al siguiente depósito de combustible o, en el paso final, para regresar a la base.

Solución a la variante "cruzar el desierto" para n  = 3, que muestra el contenido de combustible del jeep y los depósitos de combustible al inicio de cada viaje, en el punto de retorno en los primeros dos viajes y al final del viaje final.

La distancia recorrida en el último viaje es el n- ésimo número armónico , H _n . Como los números armónicos no tienen límites, es posible superar cualquier distancia dada en el último viaje, siempre que haya suficiente combustible disponible en la base. Sin embargo, la cantidad de combustible necesaria y el número de depósitos de combustible aumentan exponencialmente con la distancia a recorrer.

La variante de "cruzar el desierto" se puede resolver con una estrategia similar, excepto que ahora no hay requisito de recolectar combustible en el camino de regreso en el viaje final. Entonces, en el viaje k, el jeep establece un nuevo k -ésimo depósito de combustible a una distancia de 1/(2 n  − 2 k  + 1) unidades del depósito de combustible anterior y deja (2 n  − 2 k  − 1)/(2 n  − 2 k  + 1) unidades de combustible allí. En cada uno de los siguientes n  −  k  − 1 viajes, recoge 1/(2 n  − 2 k  + 1) unidades de combustible del k -ésimo depósito en su camino de ida y otras 1/(2 n  − 2 k  + 1) unidades de combustible en su camino de regreso.

Ahora, cuando el jeep comienza su viaje final, hay n  − 1 depósitos de combustible. El más lejano contiene 1/3 de una unidad de combustible, el siguiente más lejano contiene 1/5 de una unidad de combustible, y así sucesivamente, y el depósito de combustible más cercano tiene solo 1/(2 n  − 1) unidades de combustible restantes. Junto con 1 unidad de combustible con la que comienza desde la base, esto significa que el jeep puede recorrer una distancia total de

${\displaystyle 1+{\frac {1}{3}}+{\frac {1}{5}}+\cdots +{\frac {1}{2n-1}}=\sum _{k=1}^{n}{\frac {1}{2k-1}}=H_{2n-1}-{\frac {1}{2}}H_{n-1}\equiv \mathrm {cross} (n)}$

unidades en su último viaje. ^{[1] [3]} Recoge todo el combustible restante en cada depósito en el camino de salida, lo que llena su tanque. Después de dejar el depósito de combustible más lejano, recorre una distancia adicional de 1 unidad.

Desde

${\displaystyle \mathrm {cross} (n)=\sum _{k=1}^{n}{\frac {1}{2k-1}}>\sum _{k=1}^{n}{\frac {1}{2k}}={\frac {1}{2}}H_{n}=\mathrm {explore} (n)}$,

En teoría, es posible cruzar un desierto de cualquier tamaño si se dispone de suficiente combustible en la base. Como antes, la cantidad de combustible necesaria y el número de depósitos de combustible aumentan exponencialmente con la distancia a recorrer.

En resumen, la distancia máxima que puede alcanzar el jeep (con una capacidad de combustible para 1 unidad de distancia en cualquier momento) en n viajes (con n-1 recargas de combustible a mitad de camino y consumiendo un total de n unidades de combustible) es

• ${\displaystyle \mathrm {explore} (n)={\frac {1}{2}}H_{n}={\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{6}}+\cdots +{\frac {1}{2n}}}$, para explorar el desierto donde el jeep debe regresar a la base al final de cada viaje;
• ${\displaystyle \mathrm {cross} (n)=H_{2n-1}-{\frac {1}{2}}H_{n-1}=1+{\frac {1}{3}}+{\frac {1}{5}}+\cdots +{\frac {1}{2n-1}}}$, para cruzar el desierto donde el jeep debe regresar a la base al final de cada viaje excepto el viaje final, cuando el jeep viaja lo más lejos que puede antes de quedarse sin combustible.

Aquí está el n-ésimo número armónico . ${\displaystyle H_{n}=1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots +{\frac {1}{n}}}$

Cantidad continua de combustible

El número de unidades de combustible disponibles en la base no tiene por qué ser un número entero. En el caso general, la distancia máxima alcanzable para el problema de "explorar el desierto" con n unidades de combustible es

${\displaystyle \mathrm {explore} (n)=\int _{0}^{n}{\frac {\mathrm {d} f}{2\lceil n-f\rceil }}}$

con el primer depósito de combustible ubicado a unidades de distancia de la base de partida, el segundo a unidades de distancia del primer depósito de combustible, el tercero a unidades de distancia del segundo depósito de combustible, y así sucesivamente. Aquí está la parte fraccionaria de n . ${\displaystyle \{n\}/(2\lceil n\rceil )}$ ${\displaystyle 1/(2\lceil n\rceil -2)}$ ${\displaystyle 1/(2\lceil n\rceil -4)}$ ${\displaystyle \{n\}=n-\lfloor n\rfloor }$

La distancia máxima alcanzable para el problema de "cruzar el desierto" con n unidades de combustible es

${\displaystyle \mathrm {cross} (n)=\int _{0}^{n}{\frac {\mathrm {d} f}{2\lceil n-f\rceil -1}}}$

con el primer depósito de combustible ubicado a unidades de distancia de la base de partida, el segundo a unidades de distancia del primer depósito de combustible, el tercero a unidades de distancia del segundo depósito de combustible, y así sucesivamente. Aquí está la parte fraccionaria de n . ${\displaystyle \{n\}/(2\lceil n\rceil -1)}$ ${\displaystyle 1/(2\lceil n\rceil -3)}$ ${\displaystyle 1/(2\lceil n\rceil -5)}$ ${\displaystyle \{n\}=n-\lfloor n\rfloor }$

Orden de independencia

El orden de los viajes en jeep no es fijo. Por ejemplo, en la versión del problema de "exploración del desierto", el jeep podría hacer n − 1 viajes de ida y vuelta entre la base y el primer depósito de combustible, dejando ( n − 1) / n unidades de combustible en el depósito de combustible cada vez y luego hacer un n -ésimo viaje de ida al primer depósito de combustible, llegando así allí con un total de ( n − 1) + 1/(2 n ) unidades de combustible disponibles. Las 1/(2 n ) unidades se guardan para el viaje de regreso a la base al final y las otras n − 1 unidades de combustible se utilizan para mover combustible entre el primer y el segundo depósito de combustible, utilizando n − 2 viajes de ida y vuelta y luego un ( n − 1) -ésimo viaje de ida al segundo depósito de combustible. Y así sucesivamente.

Aplicaciones prácticas

En la Operación Black Buck One , el Vulcan atacante fue reabastecido siete veces en el viaje de ida y una vez en el de vuelta. Las líneas grises indican aviones de reserva para reemplazar a las bajas.

El problema puede tener una aplicación práctica en situaciones de guerra, especialmente en lo que respecta a la eficiencia del combustible . En el contexto del bombardeo de Japón en la Segunda Guerra Mundial por los B-29 , Robert McNamara dice en la película The Fog of War que la comprensión del problema de la eficiencia del combustible causado por tener que transportar el combustible a las bases avanzadas fue la razón principal por la que se abandonó la estrategia de lanzar bombardeos desde China continental en favor de la estrategia de salto de isla en isla :

"Teníamos que volar esos aviones desde las bases en Kansas hasta la India. Luego teníamos que volar por encima de la joroba para cargar combustible hasta China. [...] Se suponía que debíamos llevar esos B-29 , allí no había aviones cisterna . Teníamos que llenarlos de combustible, volar desde la India hasta Chengtu , descargar el combustible, volar de vuelta a la India, hacer misiones suficientes para acumular combustible en Chengtu, volar a Yawata , Japón , bombardear las fábricas de acero y volver a la India. Teníamos tan poco entrenamiento sobre este problema de maximizar la eficiencia [del combustible] que, de hecho, nos dimos cuenta de que, en lugar de descargar combustible, tenían que encargarse de traer de vuelta algunos de los B-29. Para resumir, no valía la pena. Y fue LeMay quien realmente llegó a esa conclusión y llevó a los Chiefs a trasladar todo el asunto a las Marianas , lo que devastó Japón". ^[6]

(Las misiones de bombardeo atómico al final de la Segunda Guerra Mundial se llevaron a cabo utilizando Superfortalezas B-29 desde la isla de Tinian, en el Pacífico, en las Islas Marianas del Norte ).

Véase también

• Lea la Operación Black Buck para comprender mejor la aplicación de estas ideas. En estas misiones, llevadas a cabo durante la Guerra de las Malvinas , la Real Fuerza Aérea utilizó el reabastecimiento en vuelo mediante el envío de aviones cisterna para permitir que los bombarderos Vulcan con base en la isla Ascensión bombardearan objetivos en las Islas Malvinas .
• Serie armónica (matemáticas)
• Optimización (matemáticas)

Referencias

1. Weisstein, Eric W. "Problema del Jeep". MathWorld .
2. Gardner, Martin (1994). Mis mejores acertijos matemáticos y lógicos . Dover. pp. 53. ISBN 0-486-28152-3.
3. " Problemas de exploración. Otra pregunta común se refiere a la distancia máxima en un desierto que podría alcanzar desde un asentamiento fronterizo un explorador capaz de llevar provisiones que le duraran un día." WW Rouse Ball y HSM Coxeter (1987). Mathematical Recreations and Essays , Decimotercera edición, Dover, pág. 32. ISBN 0-486-25357-0 . 
4. Problemas para agudizar a los jóvenes, John Hadley y David Singmaster, The Mathematical Gazette , 76 , #475 (marzo de 1992), págs. 102–126.
5. Logística óptima para expediciones: el problema del jeep con recarga completa, Gunter Rote y Guochuan Zhang, junio de 1996
6. Transcripción de Niebla de Guerra, www.errolmorris.com