Red neuronal convolucional

Red neuronal artificial

Una red neuronal convolucional ( CNN ) es un tipo regularizado de red neuronal de avance que aprende características por sí misma a través de la optimización del filtro (o kernel). Este tipo de red de aprendizaje profundo se ha aplicado para procesar y hacer predicciones a partir de muchos tipos diferentes de datos, incluidos texto, imágenes y audio. ^[1] Las redes basadas en convolución son el estándar de facto en los enfoques basados ​​en aprendizaje profundo para la visión por computadora y el procesamiento de imágenes, y solo recientemente han sido reemplazadas, en algunos casos, por arquitecturas de aprendizaje profundo más nuevas, como el transformador . Los gradientes que desaparecen y los gradientes explosivos, vistos durante la retropropagación en redes neuronales anteriores, se evitan mediante el uso de pesos regularizados sobre menos conexiones. ^{[2] [3]} Por ejemplo, para cada neurona en la capa completamente conectada, se requerirían 10,000 pesos para procesar una imagen de tamaño 100 × 100 píxeles. Sin embargo, al aplicar núcleos de convolución en cascada (o correlación cruzada), ^{[4] [5]} solo se requieren 25 neuronas para procesar mosaicos de tamaño 5x5. ^{[6] [7]} Las características de las capas superiores se extraen de ventanas de contexto más amplias, en comparación con las características de las capas inferiores.

Algunas aplicaciones de las CNN incluyen:

• Reconocimiento de imágenes y vídeos , ^[8]
• sistemas de recomendación , ^[9]
• clasificación de imágenes ,
• segmentación de imágenes ,
• análisis de imágenes médicas ,
• procesamiento del lenguaje natural , ^[10]
• interfaces cerebro-computadora , ^[11] y
• series temporales financieras . ^[12]

Las CNN también se conocen como redes neuronales artificiales invariantes al desplazamiento o invariantes al espacio , basadas en la arquitectura de peso compartido de los núcleos de convolución o filtros que se deslizan a lo largo de las características de entrada y brindan respuestas equivariantes a la traducción conocidas como mapas de características. ^{[13] [14]} Contrariamente a la intuición, la mayoría de las redes neuronales convolucionales no son invariantes a la traducción , debido a la operación de submuestreo que aplican a la entrada. ^[15]

Las redes neuronales de propagación hacia adelante suelen ser redes completamente conectadas, es decir, cada neurona de una capa está conectada a todas las neuronas de la siguiente capa . La "conectividad total" de estas redes las hace propensas a sobreajustar los datos. Las formas típicas de regularización, o de prevención del sobreajuste, incluyen: penalizar parámetros durante el entrenamiento (como la disminución del peso) o recortar la conectividad (conexiones omitidas, abandono, etc.). Los conjuntos de datos robustos también aumentan la probabilidad de que las CNN aprendan los principios generalizados que caracterizan a un conjunto de datos dado en lugar de los sesgos de un conjunto poco poblado. ^[16]

Las redes convolucionales se inspiraron en procesos biológicos ^{[17] [18] [19] [20]} en que el patrón de conectividad entre neuronas se asemeja a la organización de la corteza visual animal . Las neuronas corticales individuales responden a estímulos solo en una región restringida del campo visual conocida como campo receptivo . Los campos receptivos de diferentes neuronas se superponen parcialmente de tal manera que cubren todo el campo visual.

Las CNN utilizan relativamente poco preprocesamiento en comparación con otros algoritmos de clasificación de imágenes . Esto significa que la red aprende a optimizar los filtros (o núcleos) mediante aprendizaje automático, mientras que en los algoritmos tradicionales estos filtros se diseñan a mano . Esta independencia del conocimiento previo y de la intervención humana en la extracción de características es una gran ventaja. ^{[ ¿para quién? ]}

Arquitectura

Comparación de la convolución, agrupación y capas densas de LeNet y AlexNet
(el tamaño de la imagen de AlexNet debería ser 227×227×3, en lugar de 224×224×3, para que los cálculos salgan bien. El artículo original decía números diferentes, pero Andrej Karpathy, el jefe de visión por computadora en Tesla, dijo que debería ser 227×227×3 (dijo que Alex no describió por qué puso 224×224×3). La siguiente convolución debería ser 11×11 con paso 4: 55×55×96 (en lugar de 54×54×96). Se calcularía, por ejemplo, como: [(ancho de entrada 227 - ancho del kernel 11) / paso 4] + 1 = [(227 - 11) / 4] + 1 = 55. Dado que la salida del kernel tiene la misma longitud que el ancho, su área es 55×55.)

Una red neuronal convolucional consta de una capa de entrada, capas ocultas y una capa de salida. En una red neuronal convolucional, las capas ocultas incluyen una o más capas que realizan convoluciones. Normalmente, esto incluye una capa que realiza un producto escalar del núcleo de convolución con la matriz de entrada de la capa. Este producto suele ser el producto interno de Frobenius y su función de activación es comúnmente ReLU . A medida que el núcleo de convolución se desliza a lo largo de la matriz de entrada de la capa, la operación de convolución genera un mapa de características, que a su vez contribuye a la entrada de la siguiente capa. A esto le siguen otras capas como capas de agrupación , capas completamente conectadas y capas de normalización. Aquí debe notarse qué tan cerca está una red neuronal convolucional de un filtro adaptado . ^[21]

Capas convolucionales

En una CNN, la entrada es un tensor con forma:

(número de entradas) × (altura de entrada) × (ancho de entrada) × ( canales de entrada )

Después de pasar por una capa convolucional, la imagen se abstrae en un mapa de características, también llamado mapa de activación, con forma:

(número de entradas) × (altura del mapa de características) × (ancho del mapa de características) × ( canales del mapa de características ).

Las capas convolucionales convolucionan la entrada y pasan su resultado a la siguiente capa. Esto es similar a la respuesta de una neurona en la corteza visual a un estímulo específico. ^[22] Cada neurona convolucional procesa datos solo para su campo receptivo .

Ejemplo de red neuronal convolucional 1D con avance de retroalimentación

Aunque las redes neuronales de propagación hacia adelante completamente conectadas se pueden utilizar para aprender características y clasificar datos, esta arquitectura generalmente no es práctica para entradas más grandes (por ejemplo, imágenes de alta resolución), que requerirían cantidades masivas de neuronas porque cada píxel es una característica de entrada relevante. Una capa completamente conectada para una imagen de tamaño 100 × 100 tiene 10 000 pesos para cada neurona en la segunda capa. La convolución reduce la cantidad de parámetros libres, lo que permite que la red sea más profunda. ^[6] Por ejemplo, usar una región de mosaico de 5 × 5, cada una con los mismos pesos compartidos, requiere solo 25 neuronas. El uso de pesos regularizados sobre menos parámetros evita los problemas de gradientes evanescentes y gradientes explosivos observados durante la retropropagación en redes neuronales anteriores. ^{[2] [3]}

Para acelerar el procesamiento, las capas convolucionales estándar pueden reemplazarse por capas convolucionales separables en profundidad ^[23] , que se basan en una convolución en profundidad seguida de una convolución puntual. La convolución en profundidad es una convolución espacial aplicada independientemente sobre cada canal del tensor de entrada, mientras que la convolución puntual es una convolución estándar restringida al uso de núcleos. ${\displaystyle 1\times 1}$

Capas de agrupamiento

Las redes convolucionales pueden incluir capas de agrupación locales y/o globales junto con capas convolucionales tradicionales. Las capas de agrupación reducen las dimensiones de los datos al combinar las salidas de los grupos de neuronas en una capa en una sola neurona en la siguiente capa. La agrupación local combina grupos pequeños, los tamaños de mosaico como 2 × 2 se utilizan comúnmente. La agrupación global actúa sobre todas las neuronas del mapa de características. ^{[24] [25]} Hay dos tipos comunes de agrupación en uso popular: máximo y promedio. La agrupación máxima usa el valor máximo de cada grupo local de neuronas en el mapa de características, ^{[26] [27]} mientras que la agrupación promedio toma el valor promedio.

Capas completamente conectadas

Las capas completamente conectadas conectan cada neurona de una capa con cada neurona de otra capa. Es lo mismo que una red neuronal perceptiva multicapa (MLP) tradicional. La matriz aplanada pasa por una capa completamente conectada para clasificar las imágenes.

Campo receptivo

En las redes neuronales, cada neurona recibe información de una cierta cantidad de ubicaciones en la capa anterior. En una capa convolucional, cada neurona recibe información solo de un área restringida de la capa anterior llamada campo receptivo de la neurona . Normalmente, el área es un cuadrado (por ejemplo, 5 por 5 neuronas). Mientras que, en una capa completamente conectada, el campo receptivo es toda la capa anterior . Por lo tanto, en cada capa convolucional, cada neurona toma información de un área más grande en la entrada que las capas anteriores. Esto se debe a la aplicación de la convolución una y otra vez, que tiene en cuenta el valor de un píxel, así como los píxeles circundantes. Cuando se utilizan capas dilatadas, la cantidad de píxeles en el campo receptivo permanece constante, pero el campo está menos poblado a medida que sus dimensiones crecen al combinar el efecto de varias capas.

Para manipular el tamaño del campo receptivo como se desee, existen algunas alternativas a la capa convolucional estándar. Por ejemplo, la convolución atrosa o dilatada ^{[28] [29]} expande el tamaño del campo receptivo sin aumentar el número de parámetros intercalando regiones visibles y ciegas. Además, una sola capa convolucional dilatada puede comprender filtros con múltiples relaciones de dilatación, ^[30] por lo que tiene un tamaño de campo receptivo variable.

Pesos

Cada neurona de una red neuronal calcula un valor de salida aplicando una función específica a los valores de entrada recibidos del campo receptivo en la capa anterior. La función que se aplica a los valores de entrada está determinada por un vector de pesos y un sesgo (normalmente números reales). El aprendizaje consiste en ajustar iterativamente estos sesgos y pesos.

Los vectores de pesos y sesgos se denominan filtros y representan características particulares de la entrada (por ejemplo, una forma particular). Una característica distintiva de las CNN es que muchas neuronas pueden compartir el mismo filtro. Esto reduce la huella de memoria porque se utiliza un solo sesgo y un solo vector de pesos en todos los campos receptivos que comparten ese filtro, a diferencia de que cada campo receptivo tenga su propio sesgo y ponderación vectorial. ^[31]

Deconvolucional

Una red neuronal deconvolucional es básicamente lo opuesto a una red neuronal convolucional. Consta de capas deconvolucionales y capas de desagrupamiento. ^[32]

Una capa deconvolucional es la transposición de una capa convolucional. En concreto, una capa convolucional se puede escribir como una multiplicación por una matriz, y una capa deconvolucional es una multiplicación por la transposición de esa matriz. ^[33]

Una capa de desagrupamiento expande la capa. La capa de desagrupamiento máximo es la más simple, ya que simplemente copia cada entrada varias veces. Por ejemplo, una capa de desagrupamiento máximo de 2 por 2 es . ${\displaystyle [x]\mapsto {\begin{bmatrix}x&x\\x&x\end{bmatrix}}}$

Las capas de deconvolución se utilizan en los generadores de imágenes. De manera predeterminada, crean un artefacto periódico de tablero de ajedrez, que se puede corregir mediante la conversión a mayor escala y luego a convolución. ^[34]

Historia

Las CNN se comparan a menudo con la forma en que el cerebro logra el procesamiento de la visión en los organismos vivos . ^[35]

Campos receptivos en la corteza visual

Los trabajos de Hubel y Wiesel en los años 1950 y 1960 demostraron que las cortezas visuales de los gatos contienen neuronas que responden individualmente a pequeñas regiones del campo visual . Siempre que los ojos no se muevan, la región del espacio visual dentro de la cual los estímulos visuales afectan la activación de una sola neurona se conoce como su campo receptivo . ^[36] Las células vecinas tienen campos receptivos similares y superpuestos. El tamaño y la ubicación del campo receptivo varían sistemáticamente a lo largo de la corteza para formar un mapa completo del espacio visual. ^{[ cita requerida ] La corteza en cada hemisferio representa el} campo visual contralateral . ^{[ cita requerida ]}

Su artículo de 1968 identificó dos tipos básicos de células visuales en el cerebro: ^[18]

• células simples , cuya salida se maximiza mediante bordes rectos que tienen orientaciones particulares dentro de su campo receptivo
• células complejas , que tienen campos receptivos más grandes , cuya salida es insensible a la posición exacta de los bordes en el campo.

Hubel y Wiesel también propusieron un modelo en cascada de estos dos tipos de células para su uso en tareas de reconocimiento de patrones. ^{[37] [36]}

Neocognitrón, origen de la arquitectura CNN

Inspirado por el trabajo de Hubel y Wiesel, en 1969, Kunihiko Fukushima publicó una CNN profunda que utiliza la función de activación ReLU . ^[38] A diferencia de la mayoría de las redes modernas, esta red utilizaba núcleos diseñados a mano. No se utilizó en su neocognitrón, ya que todos los pesos eran no negativos; en su lugar, se utilizó la inhibición lateral. El rectificador se ha convertido en la función de activación más popular para las CNN y las redes neuronales profundas en general. ^[39]

El " neocognitrón " fue introducido por Kunihiko Fukushima en 1979. ^{[40] [19] [17]} Los núcleos fueron entrenados mediante aprendizaje no supervisado . Se inspiró en el trabajo mencionado anteriormente de Hubel y Wiesel. El neocognitrón introdujo los dos tipos básicos de capas:

• "Capa S": una capa de campo receptivo de pesos compartidos, más tarde conocida como capa convolucional, que contiene unidades cuyos campos receptivos cubren una parte de la capa anterior. Un grupo de campo receptivo de pesos compartidos (un "plano" en la terminología del neocognitrón) suele denominarse filtro, y una capa normalmente tiene varios de estos filtros.
• "Capa C": una capa de submuestreo que contiene unidades cuyos campos receptivos cubren parches de capas convolucionales anteriores. Dicha unidad normalmente calcula un promedio ponderado de las activaciones de las unidades en su parche y aplica inhibición (normalización divisiva) agrupada a partir de un parche algo más grande y a través de diferentes filtros en una capa, y aplica una función de activación de saturación. Los pesos de los parches no son negativos y no se pueden entrenar en el neocognitrón original. El submuestreo y la inhibición competitiva ayudan a clasificar características y objetos en escenas visuales incluso cuando los objetos se desplazan.

En una variante del neocognitrón llamada cresceptrón , en lugar de utilizar el promedio espacial de Fukushima con inhibición y saturación, J. Weng et al. en 1993 introdujeron un método llamado agrupamiento máximo donde una unidad de submuestreo calcula el máximo de las activaciones de las unidades en su parche. ^[41] El agrupamiento máximo se utiliza a menudo en las CNN modernas. ^[42]

A lo largo de las décadas se han propuesto varios algoritmos de aprendizaje supervisados ​​y no supervisados ​​para entrenar los pesos de un neocognitrón. ^[17] Sin embargo, hoy en día, la arquitectura CNN generalmente se entrena a través de retropropagación .

Convolución en el tiempo

El término "convolución" aparece por primera vez en redes neuronales en un artículo de Toshiteru Homma, Les Atlas y Robert Marks II en la primera Conferencia sobre Sistemas de Procesamiento de Información Neural en 1987. Su artículo reemplazó la multiplicación con convolución en el tiempo, proporcionando inherentemente invariancia de desplazamiento, motivada por y conectándose más directamente con el concepto de procesamiento de señales de un filtro , y lo demostró en una tarea de reconocimiento de voz. ^[7] También señalaron que, como un sistema entrenable con datos, la convolución es esencialmente equivalente a la correlación, ya que la inversión de los pesos no afecta la función aprendida final ("Por conveniencia, denotamos * como correlación en lugar de convolución. Tenga en cuenta que convolucionar a(t) con b(t) es equivalente a correlacionar a(-t) con b(t)"). ^[7] Las implementaciones modernas de CNN generalmente hacen correlación y la llaman convolución, por conveniencia, como lo hicieron aquí.

Redes neuronales con retardo temporal

La red neuronal con retardo temporal (TDNN) fue introducida en 1987 por Alex Waibel et al. para el reconocimiento de fonemas y fue una de las primeras redes convolucionales, ya que logró invariancia de desplazamiento. ^[43] Una TDNN es una red neuronal convolucional 1-D donde la convolución se realiza a lo largo del eje de tiempo de los datos. Es la primera CNN que utiliza el reparto de pesos en combinación con un entrenamiento por descenso de gradiente, utilizando retropropagación . ^[44] Por lo tanto, aunque también utiliza una estructura piramidal como en el neocognitrón, realizó una optimización global de los pesos en lugar de una local. ^[43]

Las TDNN son redes convolucionales que comparten pesos a lo largo de la dimensión temporal. ^[45] Permiten que las señales de voz se procesen de manera invariable en el tiempo. En 1990, Hampshire y Waibel introdujeron una variante que realiza una convolución bidimensional. ^[46] Dado que estas TDNN operaban sobre espectrogramas, el sistema de reconocimiento de fonemas resultante era invariable tanto a los cambios de tiempo como de frecuencia, como en el caso de las imágenes procesadas por un neocognitrón.

Las TDNN mejoraron el rendimiento del reconocimiento de voz a larga distancia. ^[47]

Reconocimiento de imágenes con CNN entrenadas por descenso de gradiente

Denker et al. (1989) diseñaron un sistema CNN 2-D para reconocer números de códigos postales escritos a mano . ^[48] Sin embargo, la falta de un método de entrenamiento eficiente para determinar los coeficientes del núcleo de las convoluciones involucradas significó que todos los coeficientes tuvieron que ser diseñados a mano laboriosamente. ^[49]

Siguiendo los avances en el entrenamiento de las CNN 1-D de Waibel et al. (1987), Yann LeCun et al. (1989) ^[49] utilizaron la retropropagación para aprender los coeficientes del núcleo de convolución directamente de imágenes de números escritos a mano. De este modo, el aprendizaje era completamente automático, funcionaba mejor que el diseño de coeficientes manual y era adecuado para una gama más amplia de problemas de reconocimiento de imágenes y tipos de imágenes. Wei Zhang et al. (1988) ^{[13] [14]} utilizaron la retropropagación para entrenar los núcleos de convolución de una CNN para el reconocimiento de alfabetos. El modelo se denominó red neuronal de reconocimiento de patrones invariante al cambio antes de que se acuñara el nombre CNN a principios de los años 1990. Wei Zhang et al. también aplicaron la misma CNN sin la última capa completamente conectada para la segmentación de objetos de imágenes médicas (1991) ^[50] y la detección de cáncer de mama en mamografías (1994). ^[51]

Este enfoque se convirtió en la base de la visión artificial moderna .

Agrupamiento máximo

En 1990, Yamaguchi et al. introdujeron el concepto de agrupamiento máximo, una operación de filtrado fija que calcula y propaga el valor máximo de una región dada. Lo hicieron combinando TDNN con agrupamiento máximo para lograr un sistema de reconocimiento de palabras aislado e independiente del hablante. ^[26] En su sistema utilizaron varios TDNN por palabra, uno para cada sílaba . Los resultados de cada TDNN sobre la señal de entrada se combinaron utilizando agrupamiento máximo y las salidas de las capas de agrupamiento se pasaron luego a redes que realizaban la clasificación de palabras real.

LeNet-5

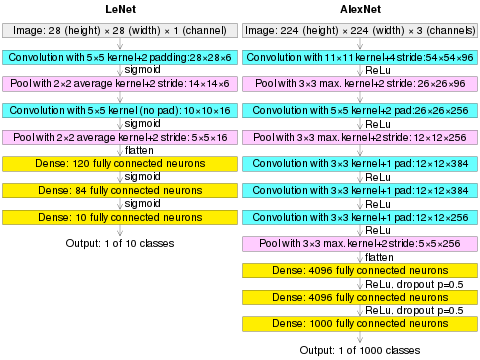
LeNet-5, una red convolucional pionera de 7 niveles diseñada por LeCun et al. en 1995, ^[52] clasifica números escritos a mano en cheques ( en inglés británico : cheques ) digitalizados en imágenes de 32x32 píxeles. La capacidad de procesar imágenes de mayor resolución requiere redes neuronales convolucionales más grandes y con más capas, por lo que esta técnica está limitada por la disponibilidad de recursos informáticos.

Era superior a otros sistemas de lectura de cheques de cortesía comerciales (a partir de 1995). El sistema se integró en los sistemas de lectura de cheques de NCR y se utilizó en varios bancos estadounidenses desde junio de 1996, leyendo millones de cheques por día. ^[53]

Red neuronal invariante al cambio

En 1988, Wei Zhang et al. propusieron una red neuronal invariante al cambio para el reconocimiento de caracteres de imágenes. ^{[13] [14]} Es un Neocognitrón modificado que conserva solo las interconexiones convolucionales entre las capas de características de la imagen y la última capa completamente conectada. El modelo se entrenó con retropropagación. El algoritmo de entrenamiento se mejoró aún más en 1991 ^[54] para mejorar su capacidad de generalización. La arquitectura del modelo se modificó eliminando la última capa completamente conectada y se aplicó para la segmentación de imágenes médicas (1991) ^[50] y la detección automática de cáncer de mama en mamografías (1994) . ^[51]

^{En 1988 [55]} se propuso un diseño diferente basado en la convolución para su aplicación en la descomposición de señales convolucionadas de electromiografía unidimensional mediante deconvolución. Este diseño se modificó en 1989 para dar lugar a otros diseños basados ​​en la deconvolución. ^{[56] [57]}

Implementaciones de GPU

Aunque las CNN se inventaron en la década de 1980, su avance en la década de 2000 requirió implementaciones rápidas en unidades de procesamiento gráfico (GPU).

En 2004, KS Oh y K. Jung demostraron que las redes neuronales estándar pueden acelerarse enormemente en las GPU. Su implementación fue 20 veces más rápida que una implementación equivalente en la CPU . ^[58] En 2005, otro artículo también destacó el valor de GPGPU para el aprendizaje automático . ^[59]

La primera implementación de una CNN en GPU fue descrita en 2006 por K. Chellapilla et al. Su implementación fue cuatro veces más rápida que una implementación equivalente en CPU. ^[60] En el mismo período, las GPU también se utilizaron para el entrenamiento no supervisado de redes de creencias profundas . ^{[61] [62] [63] [64]}

En 2010, Dan Ciresan et al. de IDSIA entrenaron redes de propagación hacia adelante profundas en GPU. ^[65] En 2011, extendieron esto a las CNN, acelerando un 60% en comparación con el entrenamiento con CPU. ^[24] En 2011, la red ganó un concurso de reconocimiento de imágenes donde lograron un rendimiento sobrehumano por primera vez. ^[66] Luego ganaron más competencias y lograron el estado del arte en varios puntos de referencia. ^{[67] [42] [27]}

Posteriormente, AlexNet , una CNN similar basada en GPU de Alex Krizhevsky et al., ganó el ImageNet Large Scale Visual Recognition Challenge 2012. ^[68] Fue un evento catalizador temprano para el auge de la IA .

En comparación con el entrenamiento de CNN mediante GPU , no se le prestó mucha atención a la CPU. (Viebke et al 2019) paraleliza CNN mediante paralelismo a nivel de subproceso y SIMD que está disponible en Intel Xeon Phi . ^{[69] [70]}

Características distintivas

En el pasado, se utilizaban modelos tradicionales de perceptrón multicapa (MLP) para el reconocimiento de imágenes. ^{[ ejemplo necesario ]} Sin embargo, la conectividad total entre nodos provocó la maldición de la dimensionalidad y era computacionalmente intratable con imágenes de mayor resolución. Una imagen de 1000 × 1000 píxeles con canales de color RGB tiene 3 millones de pesos por neurona completamente conectada, lo cual es demasiado alto para procesarlo de manera eficiente a escala.

Capas de CNN dispuestas en 3 dimensiones

Por ejemplo, en CIFAR-10 , las imágenes solo tienen un tamaño de 32×32×3 (32 de ancho, 32 de alto, 3 canales de color), por lo que una única neurona completamente conectada en la primera capa oculta de una red neuronal regular tendría 32*32*3 = 3072 pesos. Sin embargo, una imagen de 200×200 daría lugar a neuronas con 200*200*3 = 120 000 pesos.

Además, esta arquitectura de red no tiene en cuenta la estructura espacial de los datos, ya que trata los píxeles de entrada que están muy separados de la misma manera que los píxeles que están cerca. Esto ignora la localidad de referencia en los datos con una topología de cuadrícula (como las imágenes), tanto desde el punto de vista computacional como semántico. Por lo tanto, la conectividad total de las neuronas es un desperdicio para fines como el reconocimiento de imágenes, que están dominados por patrones de entrada espacialmente locales .

Las redes neuronales convolucionales son variantes de los perceptrones multicapa, diseñados para emular el comportamiento de una corteza visual . Estos modelos mitigan los desafíos que plantea la arquitectura MLP al explotar la fuerte correlación espacial local presente en las imágenes naturales. A diferencia de las MLP, las CNN tienen las siguientes características distintivas:

• Volúmenes 3D de neuronas. Las capas de una CNN tienen neuronas dispuestas en 3 dimensiones : ancho, alto y profundidad. ^[71] Donde cada neurona dentro de una capa convolucional está conectada solo a una pequeña región de la capa anterior, llamada campo receptivo. Distintos tipos de capas, tanto conectadas localmente como completamente, se apilan para formar una arquitectura CNN.
• Conectividad local: siguiendo el concepto de campos receptivos, las CNN explotan la localidad espacial al imponer un patrón de conectividad local entre neuronas de capas adyacentes. De este modo, la arquitectura garantiza que los " filtros " aprendidos produzcan la respuesta más fuerte a un patrón de entrada espacialmente local. Al apilar muchas de estas capas se obtienen filtros no lineales que se vuelven cada vez más globales (es decir, responden a una región más grande del espacio de píxeles), de modo que la red primero crea representaciones de pequeñas partes de la entrada y luego, a partir de ellas, ensambla representaciones de áreas más grandes.
• Pesos compartidos: en las CNN, cada filtro se replica en todo el campo visual. Estas unidades replicadas comparten la misma parametrización (vector de peso y sesgo) y forman un mapa de características. Esto significa que todas las neuronas en una capa convolucional dada responden a la misma característica dentro de su campo de respuesta específico. La replicación de unidades de esta manera permite que el mapa de activación resultante sea equivariante ante cambios en las ubicaciones de las características de entrada en el campo visual, es decir, garantizan la equivariancia traslacional , siempre que la capa tenga un paso de uno. ^[72]
• Agrupamiento: en las capas de agrupamiento de una CNN , los mapas de características se dividen en subregiones rectangulares y las características de cada rectángulo se muestrean de forma independiente hasta obtener un único valor, generalmente tomando su valor promedio o máximo. Además de reducir el tamaño de los mapas de características, la operación de agrupamiento otorga un grado de invariancia traslacional local a las características contenidas en ellos, lo que permite que la CNN sea más robusta a las variaciones en sus posiciones. ^[15]

En conjunto, estas propiedades permiten que las CNN logren una mejor generalización de los problemas de visión . La distribución de pesos reduce drásticamente la cantidad de parámetros libres aprendidos, lo que reduce los requisitos de memoria para ejecutar la red y permite el entrenamiento de redes más grandes y potentes.

Bloques de construcción

Una arquitectura CNN está formada por una pila de capas distintas que transforman el volumen de entrada en un volumen de salida (por ejemplo, que contiene las puntuaciones de la clase) a través de una función diferenciable. Se utilizan habitualmente algunos tipos distintos de capas, que se analizan con más detalle a continuación.

Neuronas de una capa convolucional (azul), conectadas a su campo receptivo (rojo)

Capa convolucional

Un ejemplo práctico de realización de una convolución. La convolución tiene paso 1, relleno de ceros y tamaño de núcleo 3x3. El núcleo de convolución es un operador laplaciano discreto .

La capa convolucional es el componente básico de una CNN. Los parámetros de la capa consisten en un conjunto de filtros que se pueden aprender (o núcleos ), que tienen un campo receptivo pequeño, pero se extienden a través de toda la profundidad del volumen de entrada. Durante el paso hacia adelante, cada filtro se convoluciona a lo largo del ancho y la altura del volumen de entrada, calculando el producto escalar entre las entradas del filtro y la entrada, lo que produce un mapa de activación bidimensional de ese filtro. Como resultado, la red aprende filtros que se activan cuando detecta algún tipo específico de característica en alguna posición espacial en la entrada. ^{[73] [nb 1]}

Al apilar los mapas de activación de todos los filtros a lo largo de la dimensión de profundidad se forma el volumen de salida completo de la capa de convolución. De esta forma, cada entrada del volumen de salida también se puede interpretar como una salida de una neurona que observa una pequeña región en la entrada. Cada entrada de un mapa de activación utiliza el mismo conjunto de parámetros que definen el filtro.

El aprendizaje autosupervisado se ha adaptado para su uso en capas convolucionales mediante el uso de parches dispersos con una alta relación de máscara y una capa de normalización de respuesta global. ^{[ cita requerida ]}

Conectividad local

Arquitectura típica de CNN

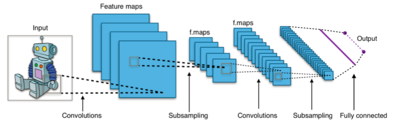
Cuando se trabaja con entradas de alta dimensión, como imágenes, no resulta práctico conectar neuronas a todas las neuronas del volumen anterior porque una arquitectura de red de este tipo no tiene en cuenta la estructura espacial de los datos. Las redes convolucionales explotan la correlación espacial local al imponer un patrón de conectividad local dispersa entre neuronas de capas adyacentes: cada neurona está conectada solo a una pequeña región del volumen de entrada.

El alcance de esta conectividad es un hiperparámetro llamado campo receptivo de la neurona. Las conexiones son locales en el espacio (a lo largo del ancho y la altura), pero siempre se extienden a lo largo de toda la profundidad del volumen de entrada. Una arquitectura de este tipo garantiza que los filtros aprendidos ( en inglés británico : learned ) produzcan la respuesta más fuerte a un patrón de entrada local en el espacio.

Disposición espacial

Tres hiperparámetros controlan el tamaño del volumen de salida de la capa convolucional: la profundidad, el paso y el tamaño del relleno:

• La profundidad del volumen de salida controla la cantidad de neuronas en una capa que se conectan a la misma región del volumen de entrada. Estas neuronas aprenden a activarse para diferentes características en la entrada. Por ejemplo, si la primera capa convolucional toma la imagen sin procesar como entrada, entonces diferentes neuronas a lo largo de la dimensión de profundidad pueden activarse en presencia de varios bordes orientados o manchas de color.
• El paso controla cómo se asignan las columnas de profundidad alrededor del ancho y la altura. Si el paso es 1, movemos los filtros un píxel a la vez. Esto genera una superposición importante de los campos receptivos entre las columnas y grandes volúmenes de salida. Para cualquier número entero,un paso S significa que el filtro se traslada S unidades a la vez por salida. En la práctica,es poco común. Un paso mayor significa una superposición menor de los campos receptivos y dimensiones espaciales más pequeñas del volumen de salida. ^[74] ${\textstyle S>0,}$ ${\textstyle S\geq 3}$
• A veces, resulta conveniente rellenar la entrada con ceros (u otros valores, como el promedio de la región) en el borde del volumen de entrada. El tamaño de este relleno es un tercer hiperparámetro. El relleno permite controlar el tamaño espacial del volumen de salida. En particular, a veces es deseable conservar exactamente el tamaño espacial del volumen de entrada; esto se conoce comúnmente como relleno "mismo".

Tres ejemplos de condiciones de relleno. La condición de replicación significa que el píxel exterior se rellena con el píxel más cercano en el interior. El relleno de reflexión es donde el píxel exterior se rellena con el píxel interior, reflejado a través del límite de la imagen. El relleno circular es donde el píxel exterior se envuelve hasta el otro lado de la imagen.

El tamaño espacial del volumen de salida es una función del tamaño del volumen de entrada , el tamaño del campo kernel de las neuronas de la capa convolucional, el paso y la cantidad de relleno de ceros en el borde. La cantidad de neuronas que "caben" en un volumen determinado es entonces: ${\displaystyle W}$ ${\displaystyle K}$ ${\displaystyle S}$ ${\displaystyle P}$

$${\displaystyle {\frac {W-K+2P}{S}}+1.}$$

Si este número no es un entero , entonces los pasos son incorrectos y las neuronas no se pueden colocar en mosaico para que encajen en el volumen de entrada de manera simétrica . En general, establecer el relleno en cero cuando el paso es garantiza que el volumen de entrada y el volumen de salida tendrán el mismo tamaño espacialmente. Sin embargo, no siempre es completamente necesario utilizar todas las neuronas de la capa anterior. Por ejemplo, un diseñador de redes neuronales puede decidir utilizar solo una parte del relleno. ${\textstyle P=(K-1)/2}$ ${\displaystyle S=1}$

Intercambio de parámetros

En las capas convolucionales se utiliza un esquema de compartición de parámetros para controlar la cantidad de parámetros libres. Se basa en el supuesto de que si una característica de parche es útil para calcular en alguna posición espacial, entonces también debería ser útil para calcular en otras posiciones. Al designar una sola porción bidimensional de profundidad como porción de profundidad , las neuronas en cada porción de profundidad están limitadas a usar los mismos pesos y sesgo.

Dado que todas las neuronas en un solo corte de profundidad comparten los mismos parámetros, el paso hacia adelante en cada corte de profundidad de la capa convolucional se puede calcular como una convolución de los pesos de la neurona con el volumen de entrada. ^{[nb 2]} Por lo tanto, es común referirse a los conjuntos de pesos como un filtro (o un núcleo ), que se convoluciona con la entrada. El resultado de esta convolución es un mapa de activación , y el conjunto de mapas de activación para cada filtro diferente se apilan juntos a lo largo de la dimensión de profundidad para producir el volumen de salida. El uso compartido de parámetros contribuye a la invariancia de la traducción de la arquitectura CNN. ^[15]

A veces, la suposición de compartir parámetros puede no tener sentido. Este es especialmente el caso cuando las imágenes de entrada a una CNN tienen una estructura centrada específica; para la cual esperamos que se aprendan características completamente diferentes en diferentes ubicaciones espaciales. Un ejemplo práctico es cuando las entradas son caras que se han centrado en la imagen: podríamos esperar que se aprendan diferentes características específicas de los ojos o del cabello en diferentes partes de la imagen. En ese caso, es común relajar el esquema de compartir parámetros y, en su lugar, simplemente llamar a la capa una "capa conectada localmente".

Capa de agrupamiento

Ejemplo trabajado de 2x2 maxpooling con paso 2.

Agrupamiento máximo con un filtro 2x2 y paso = 2

Otro concepto importante de las CNN es el agrupamiento, que se utiliza como una forma de submuestreo no lineal . El agrupamiento proporciona submuestreo porque reduce las dimensiones espaciales (altura y ancho) de los mapas de características de entrada mientras retiene la información más importante. Hay varias funciones no lineales para implementar el agrupamiento, donde el agrupamiento máximo y el agrupamiento promedio son los más comunes. El agrupamiento agrega información de pequeñas regiones de la entrada creando particiones del mapa de características de entrada, generalmente usando una ventana de tamaño fijo (como 2x2) y aplicando un paso (a menudo 2) para mover la ventana a lo largo de la entrada. ^[75] Nótese que sin usar un paso mayor que 1, el agrupamiento no realizaría el submuestreo, ya que simplemente movería la ventana de agrupamiento a lo largo de la entrada un paso a la vez, sin reducir el tamaño del mapa de características. En otras palabras, el paso es lo que realmente causa el submuestreo al determinar cuánto se mueve la ventana de agrupamiento sobre la entrada.

Intuitivamente, la ubicación exacta de una característica es menos importante que su ubicación aproximada en relación con otras características. Esta es la idea detrás del uso de agrupamiento en redes neuronales convolucionales. La capa de agrupamiento sirve para reducir progresivamente el tamaño espacial de la representación, para reducir el número de parámetros, la huella de memoria y la cantidad de computación en la red, y por lo tanto también para controlar el sobreajuste . Esto se conoce como submuestreo. Es común insertar periódicamente una capa de agrupamiento entre capas convolucionales sucesivas (cada una típicamente seguida por una función de activación, como una capa ReLU) en una arquitectura CNN. ^{[73] : 460–461} Si bien las capas de agrupamiento contribuyen a la invariancia de traducción local, no proporcionan invariancia de traducción global en una CNN, a menos que se use una forma de agrupamiento global. ^{[15] [72]} La capa de agrupamiento comúnmente opera independientemente en cada profundidad, o porción, de la entrada y la redimensiona espacialmente. Una forma muy común de agrupamiento máximo es una capa con filtros de tamaño 2×2, aplicados con un paso de 2, que submuestrea cada porción de profundidad en la entrada por 2 a lo largo del ancho y la altura, descartando el 75 % de las activaciones: En este caso, cada operación máxima es sobre 4 números. La dimensión de profundidad permanece sin cambios (esto también es válido para otras formas de agrupamiento). $${\displaystyle f_{X,Y}(S)=\max _{a,b=0}^{1}S_{2X+a,2Y+b}.}$$

Además de la agrupación máxima, las unidades de agrupación pueden utilizar otras funciones, como la agrupación promedio o la agrupación de norma ℓ 2. La agrupación promedio se utilizó a menudo históricamente, pero recientemente ha caído en desuso en comparación con la agrupación máxima, que generalmente funciona mejor en la práctica. ^[76]

Debido a los efectos de la rápida reducción espacial del tamaño de la representación, ^{[¿ cuál? ]} existe una tendencia reciente hacia el uso de filtros más pequeños ^[77] o a descartar por completo las capas de agrupamiento. ^[78]

Agrupación de ROI con un tamaño de 2x2. En este ejemplo, la propuesta de región (un parámetro de entrada) tiene un tamaño de 7x5.

Agrupamiento máximo de canales

Una capa de operación de agrupación máxima de canales (CMP) lleva a cabo la operación MP a lo largo del lado del canal entre las posiciones correspondientes de los mapas de características consecutivos con el fin de eliminar la información redundante. La CMP hace que las características significativas se reúnan en menos canales, lo que es importante para la clasificación de imágenes de grano fino que necesita características más discriminantes. Mientras tanto, otra ventaja de la operación CMP es hacer que el número de canales de los mapas de características sea más pequeño antes de que se conecte a la primera capa completamente conectada (FC). De manera similar a la operación MP, denotamos los mapas de características de entrada y los mapas de características de salida de una capa CMP como F ∈ R(C×M×N) y C ∈ R(c×M×N), respectivamente, donde C y c son los números de canal de los mapas de características de entrada y salida, M y N son los anchos y la altura de los mapas de características, respectivamente. Tenga en cuenta que la operación CMP solo cambia el número de canal de los mapas de características. El ancho y la altura de los mapas de características no se modifican, lo que es diferente de la operación MP. ^[79]

Consulte ^{[80] [81]} para obtener revisiones de los métodos de agrupamiento.

Capa ReLU

ReLU es la abreviatura de unidad lineal rectificada . Fue propuesta por Alston Householder en 1941, ^[82] y utilizada en CNN por Kunihiko Fukushima en 1969. ^{[38] ReLU aplica la} función de activación no saturada . ^[68] Elimina eficazmente los valores negativos de un mapa de activación estableciéndolos en cero. ^[83] Introduce no linealidad en la función de decisión y en la red general sin afectar los campos receptivos de las capas de convolución. En 2011, Xavier Glorot, Antoine Bordes y Yoshua Bengio descubrieron que ReLU permite un mejor entrenamiento de redes más profundas, ^[84] en comparación con las funciones de activación ampliamente utilizadas antes de 2011. ${\textstyle f(x)=\max(0,x)}$

También se pueden utilizar otras funciones para aumentar la no linealidad, por ejemplo, la tangente hiperbólica saturada , y la función sigmoidea . ReLU suele preferirse a otras funciones porque entrena la red neuronal varias veces más rápido sin una penalización significativa de la precisión de generalización . ^[85] ${\displaystyle f(x)=\tanh(x)}$ ${\displaystyle f(x)=|\tanh(x)|}$ ${\textstyle \sigma (x)=(1+e^{-x})^{-1}}$

Capa completamente conectada

Después de varias capas de agrupación máxima y convolucional, la clasificación final se realiza mediante capas completamente conectadas. Las neuronas en una capa completamente conectada tienen conexiones con todas las activaciones en la capa anterior, como se ve en redes neuronales artificiales regulares (no convolucionales) . Por lo tanto, sus activaciones se pueden calcular como una transformación afín , con multiplicación de matrices seguida de un desplazamiento de sesgo ( suma vectorial de un término de sesgo aprendido o fijo).

Capa de pérdida

La "capa de pérdida", o " función de pérdida ", especifica cómo el entrenamiento penaliza la desviación entre la salida prevista de la red y las etiquetas de datos reales (durante el aprendizaje supervisado). Se pueden utilizar varias funciones de pérdida , según la tarea específica.

La función de pérdida Softmax se utiliza para predecir una sola clase de K clases mutuamente excluyentes. ^{[nb 3] La pérdida} de entropía cruzada sigmoidea se utiliza para predecir K valores de probabilidad independientes en . La pérdida euclidiana se utiliza para realizar regresión a etiquetas de valor real . ${\displaystyle [0,1]}$ ${\displaystyle (-\infty ,\infty )}$

Hiperparámetros

Los hiperparámetros son diversas configuraciones que se utilizan para controlar el proceso de aprendizaje. Las CNN utilizan más hiperparámetros que un perceptrón multicapa (MLP) estándar.

Tamaño del núcleo

El núcleo es la cantidad de píxeles procesados ​​en conjunto. Normalmente se expresa como las dimensiones del núcleo, por ejemplo, 2x2 o 3x3.

Relleno

El relleno es la adición de píxeles de valor (normalmente) 0 en los bordes de una imagen. Esto se hace para que los píxeles del borde no se subestimen (se pierdan) en la salida porque normalmente participarían en una única instancia de campo receptivo. El relleno aplicado es normalmente uno menos que la dimensión del núcleo correspondiente. Por ejemplo, una capa convolucional que utilice núcleos de 3x3 recibiría un relleno de 2 píxeles, es decir, 1 píxel en cada lado de la imagen. ^{[ cita requerida ]}

Paso

El paso es la cantidad de píxeles que se mueve la ventana de análisis en cada iteración. Un paso de 2 significa que cada núcleo está desplazado 2 píxeles respecto de su predecesor.

Número de filtros

Dado que el tamaño del mapa de características disminuye con la profundidad, las capas cercanas a la capa de entrada tienden a tener menos filtros, mientras que las capas superiores pueden tener más. Para igualar el cálculo en cada capa, el producto de los valores de las características v _a con la posición de los píxeles se mantiene aproximadamente constante en todas las capas. Para preservar más información sobre la entrada, sería necesario mantener la cantidad total de activaciones (cantidad de mapas de características multiplicada por la cantidad de posiciones de píxeles) sin disminuir de una capa a la siguiente.

La cantidad de mapas de características controla directamente la capacidad y depende de la cantidad de ejemplos disponibles y de la complejidad de la tarea.

Tamaño del filtro

Los tamaños de filtro habituales que se encuentran en la literatura varían mucho y, por lo general, se eligen en función del conjunto de datos. Los tamaños de filtro típicos varían de 1x1 a 7x7. Como dos ejemplos famosos, AlexNet utilizó 3x3, 5x5 y 11x11. Inceptionv3 utilizó 1x1, 3x3 y 5x5.

El desafío es encontrar el nivel adecuado de granularidad para crear abstracciones en la escala apropiada, dado un conjunto de datos particular y sin sobreajuste .

Tipo y tamaño de agrupación

Generalmente se utiliza el agrupamiento máximo , a menudo con una dimensión de 2x2. Esto implica que la entrada se reduce drásticamente , lo que reduce el costo de procesamiento.

Una mayor agrupación reduce la dimensión de la señal y puede dar como resultado una pérdida de información inaceptable . A menudo, las ventanas de agrupación que no se superponen funcionan mejor. ^[76]

Dilatación

La dilatación implica ignorar los píxeles dentro de un núcleo. Esto reduce potencialmente el procesamiento/memoria sin una pérdida significativa de señal. Una dilatación de 2 en un núcleo de 3x3 expande el núcleo a 5x5, mientras que aún procesa 9 píxeles (espaciados uniformemente). En consecuencia, una dilatación de 4 expande el núcleo a 7x7. ^{[ cita requerida ]}

Equivariancia de traducción y aliasing

Se asume comúnmente que las CNN son invariantes a los cambios de la entrada. Las capas de convolución o agrupamiento dentro de una CNN que no tienen un paso mayor que uno son de hecho equivariantes a las traslaciones de la entrada. ^[72] Sin embargo, las capas con un paso mayor que uno ignoran el teorema de muestreo de Nyquist-Shannon y podrían conducir a aliasing de la señal de entrada ^[72] Si bien, en principio, las CNN son capaces de implementar filtros anti-aliasing, se ha observado que esto no sucede en la práctica ^[86] y producen modelos que no son equivariantes a las traslaciones. Además, si una CNN hace uso de capas completamente conectadas, la equivariancia de la traslación no implica invariancia de la traslación, ya que las capas completamente conectadas no son invariantes a los cambios de la entrada. ^{[87] [15]} Una solución para la invariancia de la traslación completa es evitar cualquier submuestreo en toda la red y aplicar agrupamiento promedio global en la última capa. ^[72] Además, se han propuesto varias otras soluciones parciales, como el anti-aliasing antes de las operaciones de submuestreo, ^[88] redes de transformadores espaciales, ^[89] aumento de datos , submuestreo combinado con agrupamiento, ^[15] y redes neuronales de cápsula . ^[90]

Evaluación

La precisión del modelo final se basa en una subparte del conjunto de datos que se separa al principio, a menudo denominada conjunto de prueba. En otras ocasiones, se aplican métodos como la validación cruzada de k -fold. Otras estrategias incluyen el uso de predicción conforme . ^{[91] [92]}

Métodos de regularización

La regularización es un proceso de introducción de información adicional para resolver un problema mal planteado o para evitar un sobreajuste . Las CNN utilizan varios tipos de regularización.

Empírico

Abandonar

Debido a que una capa completamente conectada ocupa la mayoría de los parámetros, es propensa al sobreajuste. Un método para reducir el sobreajuste es el dropout , introducido en 2014. ^[93] En cada etapa de entrenamiento, los nodos individuales son "eliminados" de la red (ignorados) con probabilidad o mantenidos con probabilidad , de modo que queda una red reducida; los bordes entrantes y salientes de un nodo eliminado también se eliminan. Solo la red reducida se entrena en los datos en esa etapa. Los nodos eliminados se reinsertan luego en la red con sus pesos originales. ${\displaystyle 1-p}$ ${\displaystyle p}$

En las etapas de entrenamiento, normalmente es 0,5; para los nodos de entrada, normalmente es mucho mayor porque la información se pierde directamente cuando se ignoran los nodos de entrada. ${\displaystyle p}$

En el momento de la prueba, una vez finalizado el entrenamiento, lo ideal sería encontrar un promedio de muestra de todas las posibles redes abandonadas; desafortunadamente, esto no es factible para valores grandes de . Sin embargo, podemos encontrar una aproximación utilizando la red completa con la salida de cada nodo ponderada por un factor de , por lo que el valor esperado de la salida de cualquier nodo es el mismo que en las etapas de entrenamiento. Esta es la mayor contribución del método de abandono: aunque genera redes neuronales de manera efectiva y, como tal, permite la combinación de modelos, en el momento de la prueba solo es necesario probar una única red. ${\displaystyle 2^{n}}$ ${\displaystyle n}$ ${\displaystyle p}$ ${\displaystyle 2^{n}}$

Al evitar entrenar todos los nodos con todos los datos de entrenamiento, la deserción disminuye el sobreajuste. El método también mejora significativamente la velocidad de entrenamiento. Esto hace que la combinación de modelos sea práctica, incluso para redes neuronales profundas . La técnica parece reducir las interacciones de los nodos, lo que los lleva a aprender características más sólidas ^{[ aclaración necesaria ]} que se generalizan mejor a nuevos datos.

Conexión DropConnect

DropConnect es la generalización de dropout en la que cada conexión, en lugar de cada unidad de salida, se puede descartar con una probabilidad . De este modo, cada unidad recibe una entrada de un subconjunto aleatorio de unidades en la capa anterior. ^[94] ${\displaystyle 1-p}$

DropConnect es similar a Dropout, ya que introduce escasez dinámica dentro del modelo, pero se diferencia en que la escasez se encuentra en los pesos, en lugar de en los vectores de salida de una capa. En otras palabras, la capa completamente conectada con DropConnect se convierte en una capa escasamente conectada en la que las conexiones se eligen al azar durante la etapa de entrenamiento.

Agrupamiento estocástico

Una desventaja importante de Dropout es que no tiene los mismos beneficios para las capas convolucionales, donde las neuronas no están completamente conectadas.

Incluso antes de Dropout, en 2013, una técnica llamada agrupación estocástica ^{[95] , las operaciones de agrupación} deterministas convencionales fueron reemplazadas por un procedimiento estocástico, donde la activación dentro de cada región de agrupación se elige aleatoriamente de acuerdo con una distribución multinomial , dada por las actividades dentro de la región de agrupación. Este enfoque está libre de hiperparámetros y se puede combinar con otros enfoques de regularización, como el abandono y el aumento de datos .

Una visión alternativa del agrupamiento estocástico es que es equivalente al agrupamiento máximo estándar pero con muchas copias de una imagen de entrada, cada una con pequeñas deformaciones locales . Esto es similar a las deformaciones elásticas explícitas de las imágenes de entrada, ^[96] que ofrece un excelente rendimiento en el conjunto de datos MNIST . ^[96] El uso del agrupamiento estocástico en un modelo multicapa proporciona un número exponencial de deformaciones, ya que las selecciones en las capas superiores son independientes de las inferiores.

Datos artificiales

Dado que el grado de sobreajuste del modelo está determinado tanto por su potencia como por la cantidad de entrenamiento que recibe, proporcionar una red convolucional con más ejemplos de entrenamiento puede reducir el sobreajuste. Dado que a menudo no hay suficientes datos disponibles para entrenar, especialmente si se considera que una parte debe reservarse para pruebas posteriores, existen dos enfoques: generar nuevos datos desde cero (si es posible) o perturbar los datos existentes para crear otros nuevos. Este último enfoque se utiliza desde mediados de los años 1990. ^[52] Por ejemplo, las imágenes de entrada se pueden recortar, rotar o reescalar para crear nuevos ejemplos con las mismas etiquetas que el conjunto de entrenamiento original. ^[97]

Explícito

Parada temprana

Uno de los métodos más simples para evitar el sobreajuste de una red es simplemente detener el entrenamiento antes de que el sobreajuste haya tenido la oportunidad de ocurrir. Esto tiene la desventaja de que se detiene el proceso de aprendizaje.

Número de parámetros

Otra forma sencilla de evitar el sobreajuste es limitar la cantidad de parámetros, normalmente limitando la cantidad de unidades ocultas en cada capa o limitando la profundidad de la red. En el caso de las redes convolucionales, el tamaño del filtro también afecta la cantidad de parámetros. Limitar la cantidad de parámetros restringe directamente el poder predictivo de la red, lo que reduce la complejidad de la función que puede realizar sobre los datos y, por lo tanto, limita la cantidad de sobreajuste. Esto es equivalente a una " norma cero ".

Decaimiento del peso

Una forma sencilla de regularizador añadido es la descomposición de pesos, que simplemente añade un error adicional, proporcional a la suma de pesos ( norma L1 ) o magnitud al cuadrado ( norma L2 ) del vector de pesos, al error en cada nodo. El nivel de complejidad aceptable del modelo se puede reducir aumentando la constante de proporcionalidad (hiperparámetro 'alfa'), lo que aumenta la penalización para vectores de pesos grandes.

La regularización L2 es la forma más común de regularización. Se puede implementar penalizando la magnitud al cuadrado de todos los parámetros directamente en el objetivo. La regularización L2 tiene la interpretación intuitiva de penalizar fuertemente los vectores de peso con picos y preferir los vectores de peso difusos. Debido a las interacciones multiplicativas entre pesos y entradas, esto tiene la propiedad útil de alentar a la red a usar un poco todas sus entradas en lugar de usar mucho algunas de ellas.

La regularización L1 también es común. Hace que los vectores de peso sean dispersos durante la optimización. En otras palabras, las neuronas con regularización L1 terminan utilizando solo un subconjunto disperso de sus entradas más importantes y se vuelven casi invariantes a las entradas ruidosas. La regularización L1 con L2 se puede combinar; esto se llama regularización de red elástica .

Restricciones de norma máxima

Otra forma de regularización es imponer un límite superior absoluto a la magnitud del vector de peso para cada neurona y utilizar el descenso de gradiente proyectado para imponer la restricción. En la práctica, esto corresponde a realizar la actualización de parámetros de manera normal y luego imponer la restricción fijando el vector de peso de cada neurona para satisfacer . Los valores típicos de son del orden de 3-4. Algunos artículos informan mejoras ^[98] al utilizar esta forma de regularización. ${\displaystyle {\vec {w}}}$ ${\displaystyle \|{\vec {w}}\|_{2}<c}$ ${\displaystyle c}$

Marcos de coordenadas jerárquicos

La agrupación hace que se pierdan las relaciones espaciales precisas entre las partes de alto nivel (como la nariz y la boca en una imagen de un rostro). Estas relaciones son necesarias para el reconocimiento de la identidad. La superposición de los conjuntos de modo que cada característica aparezca en varios conjuntos ayuda a retener la información. La traducción por sí sola no puede extrapolar la comprensión de las relaciones geométricas a un punto de vista radicalmente nuevo, como una orientación o escala diferente. Por otro lado, las personas son muy buenas en la extrapolación; después de ver una nueva forma una vez, pueden reconocerla desde un punto de vista diferente. ^[99]

Una forma común de abordar este problema es entrenar la red con datos transformados en diferentes orientaciones, escalas, iluminación, etc., de modo que la red pueda hacer frente a estas variaciones. Esto requiere un gran esfuerzo computacional para grandes conjuntos de datos. La alternativa es utilizar una jerarquía de marcos de coordenadas y utilizar un grupo de neuronas para representar una conjunción de la forma de la característica y su postura relativa a la retina . La postura relativa a la retina es la relación entre el marco de coordenadas de la retina y el marco de coordenadas de las características intrínsecas. ^[100]

Por lo tanto, una forma de representar algo es incrustar el marco de coordenadas dentro de él. Esto permite que se reconozcan grandes características utilizando la consistencia de las poses de sus partes (por ejemplo, las poses de la nariz y la boca hacen una predicción consistente de la pose de toda la cara). Este enfoque garantiza que la entidad de nivel superior (por ejemplo, la cara) esté presente cuando el nivel inferior (por ejemplo, la nariz y la boca) concuerde en su predicción de la pose. Los vectores de actividad neuronal que representan la pose ("vectores de pose") permiten transformaciones espaciales modeladas como operaciones lineales que facilitan que la red aprenda la jerarquía de las entidades visuales y generalice a través de los puntos de vista. Esto es similar a la forma en que el sistema visual humano impone marcos de coordenadas para representar formas. ^[101]

Aplicaciones

Reconocimiento de imágenes

Las CNN se utilizan a menudo en sistemas de reconocimiento de imágenes . En 2012, se informó de una tasa de error del 0,23 % en la base de datos MNIST . ^[27] Otro artículo sobre el uso de CNN para la clasificación de imágenes informó de que el proceso de aprendizaje era "sorprendentemente rápido"; en el mismo artículo, los mejores resultados publicados hasta 2011 se consiguieron en la base de datos MNIST y en la base de datos NORB. ^[24] Posteriormente, una CNN similar llamada AlexNet ^[102] ganó el ImageNet Large Scale Visual Recognition Challenge 2012.

Cuando se aplicaron al reconocimiento facial , las CNN lograron una gran disminución en la tasa de error. ^[103] Otro artículo informó una tasa de reconocimiento del 97,6% en "5600 imágenes fijas de más de 10 sujetos". ^[20] Las CNN se utilizaron para evaluar la calidad del video de manera objetiva después del entrenamiento manual; el sistema resultante tuvo un error cuadrático medio muy bajo . ^[104]

El desafío de reconocimiento visual a gran escala de ImageNet es un punto de referencia en la clasificación y detección de objetos, con millones de imágenes y cientos de clases de objetos. En el ILSVRC 2014, ^[105] un desafío de reconocimiento visual a gran escala, casi todos los equipos mejor clasificados utilizaron CNN como su marco básico. El ganador GoogLeNet ^[106] (la base de DeepDream ) aumentó la precisión promedio de detección de objetos a 0,439329 y redujo el error de clasificación a 0,06656, el mejor resultado hasta la fecha. Su red aplicó más de 30 capas. Ese rendimiento de las redes neuronales convolucionales en las pruebas de ImageNet fue cercano al de los humanos. ^[107] Los mejores algoritmos aún tienen dificultades con objetos pequeños o delgados, como una pequeña hormiga en el tallo de una flor o una persona que sostiene una pluma en la mano. También tienen problemas con imágenes que se han distorsionado con filtros, un fenómeno cada vez más común con las cámaras digitales modernas. Por el contrario, ese tipo de imágenes rara vez preocupan a los humanos. Sin embargo, los humanos tienden a tener problemas con otras cuestiones. Por ejemplo, no son buenos para clasificar objetos en categorías de grano fino, como la raza particular de perro o especie de ave, mientras que las redes neuronales convolucionales se encargan de esto. ^{[ cita requerida ]}

En 2015, una CNN de múltiples capas demostró la capacidad de detectar rostros desde una amplia gama de ángulos, incluso boca abajo, incluso cuando estaban parcialmente ocluidos, con un rendimiento competitivo. La red se entrenó con una base de datos de 200.000 imágenes que incluían rostros en varios ángulos y orientaciones y otros 20 millones de imágenes sin rostros. Utilizaron lotes de 128 imágenes a lo largo de 50.000 iteraciones. ^[108]

Análisis de vídeo

En comparación con los dominios de datos de imágenes, hay relativamente poco trabajo sobre la aplicación de las CNN a la clasificación de videos. El video es más complejo que las imágenes, ya que tiene otra dimensión (temporal). Sin embargo, se han explorado algunas extensiones de las CNN en el dominio del video. Un enfoque es tratar el espacio y el tiempo como dimensiones equivalentes de la entrada y realizar convoluciones tanto en el tiempo como en el espacio. ^{[109] [110]} Otra forma es fusionar las características de dos redes neuronales convolucionales, una para el flujo espacial y otra para el temporal. ^{[111] [112] [113] Las unidades} recurrentes de memoria a corto plazo larga (LSTM) generalmente se incorporan después de la CNN para tener en cuenta las dependencias entre cuadros o entre clips. ^{[114] [115] Se han introducido esquemas} de aprendizaje no supervisado para entrenar características espaciotemporales, basados ​​en máquinas de Boltzmann restringidas con compuerta convolucional ^[116] y análisis de subespacio independiente. ^[117] Su aplicación se puede ver en el modelo de texto a video . ^{[ cita requerida ]}

Procesamiento del lenguaje natural

Las CNN también se han explorado para el procesamiento del lenguaje natural . Los modelos CNN son efectivos para varios problemas de PNL y lograron excelentes resultados en análisis semántico , ^[118] recuperación de consultas de búsqueda, ^[119] modelado de oraciones, ^[120] clasificación, ^[121] predicción ^[122] y otras tareas tradicionales de PNL. ^[123] En comparación con los métodos de procesamiento del lenguaje tradicionales, como las redes neuronales recurrentes , las CNN pueden representar diferentes realidades contextuales del lenguaje que no dependen de un supuesto de serie-secuencia, mientras que las RNN son más adecuadas cuando se requiere un modelado clásico de series de tiempo. ^{[124] [125] [126] [127]}

Detección de anomalías

Se utilizó una CNN con convoluciones 1-D en series de tiempo en el dominio de frecuencia (residuo espectral) mediante un modelo no supervisado para detectar anomalías en el dominio del tiempo. ^[128]

Descubrimiento de fármacos

Las CNN se han utilizado en el descubrimiento de fármacos . La predicción de la interacción entre moléculas y proteínas biológicas puede identificar posibles tratamientos. En 2015, Atomwise presentó AtomNet, la primera red neuronal de aprendizaje profundo para el diseño de fármacos basado en la estructura . ^[129] El sistema se entrena directamente en representaciones tridimensionales de interacciones químicas. De manera similar a cómo las redes de reconocimiento de imágenes aprenden a componer características más pequeñas y espacialmente próximas en estructuras más grandes y complejas, ^[130] AtomNet descubre características químicas, como la aromaticidad , los carbonos sp3 y los enlaces de hidrógeno . Posteriormente, AtomNet se utilizó para predecir nuevas biomoléculas candidatas para múltiples objetivos de enfermedades, en particular los tratamientos para el virus del Ébola ^[131] y la esclerosis múltiple . ^[132]

Juego de damas

Las redes neuronales convolucionales se han utilizado en el juego de damas . Entre 1999 y 2001, Fogel y Chellapilla publicaron artículos que mostraban cómo una red neuronal convolucional podía aprender a jugar a las damas mediante la coevolución. El proceso de aprendizaje no utilizó partidas profesionales humanas anteriores, sino que se centró en un conjunto mínimo de información contenida en el tablero de damas: la ubicación y el tipo de piezas, y la diferencia en el número de piezas entre los dos lados. Finalmente, el programa ( Blondie24 ) se probó en 165 partidas contra jugadores y se clasificó en el 0,4 % más alto. ^{[133] [134]} También obtuvo una victoria contra el programa Chinook en su nivel de juego "experto". ^[135]

Ir

Las CNN se han utilizado en el Go por ordenador . En diciembre de 2014, Clark y Storkey publicaron un artículo que mostraba que una CNN entrenada mediante aprendizaje supervisado a partir de una base de datos de juegos profesionales humanos podía superar a GNU Go y ganar algunos juegos contra Fuego 1.1, un buscador de árboles de Monte Carlo, en una fracción del tiempo que le tomó a Fuego jugar. ^[136] Más tarde se anunció que una gran red neuronal convolucional de 12 capas había predicho correctamente el movimiento profesional en el 55% de las posiciones, igualando la precisión de un jugador humano de 6 dan . Cuando la red convolucional entrenada se utilizó directamente para jugar partidas de Go, sin ninguna búsqueda, superó al programa de búsqueda tradicional GNU Go en el 97% de las partidas e igualó el rendimiento del programa de búsqueda de árboles de Monte Carlo Fuego, simulando diez mil jugadas (alrededor de un millón de posiciones) por movimiento. ^[137]

AlphaGo , el primero en vencer al mejor jugador humano en ese momento, utilizó un par de CNN para elegir movimientos a intentar ("red de políticas") y evaluar posiciones ("red de valores") que impulsaban MCTS. ^[138]

Pronóstico de series temporales

Las redes neuronales recurrentes generalmente se consideran las mejores arquitecturas de redes neuronales para el pronóstico de series de tiempo (y el modelado de secuencias en general), pero estudios recientes muestran que las redes convolucionales pueden tener un rendimiento comparable o incluso mejor. ^{[139] [12]} Las convoluciones dilatadas ^[140] podrían permitir que las redes neuronales convolucionales unidimensionales aprendan de manera efectiva las dependencias de las series de tiempo. ^[141] Las convoluciones se pueden implementar de manera más eficiente que las soluciones basadas en RNN, y no sufren de gradientes que desaparecen (o explotan). ^[142] Las redes convolucionales pueden proporcionar un rendimiento de pronóstico mejorado cuando hay múltiples series de tiempo similares de las que aprender. ^[143] Las CNN también se pueden aplicar a otras tareas en el análisis de series de tiempo (por ejemplo, clasificación de series de tiempo ^[144] o pronóstico cuantil ^[145] ).

Patrimonio cultural y conjuntos de datos 3D

A medida que los hallazgos arqueológicos, como tablillas de arcilla con escritura cuneiforme , se adquieren cada vez más mediante escáneres 3D , se están volviendo disponibles conjuntos de datos de referencia, incluido HeiCuBeDa ^[146] que proporciona casi 2000 conjuntos de datos 2-D y 3-D normalizados preparados con el marco de software GigaMesh . ^[147] Por lo tanto, las medidas basadas en la curvatura se utilizan junto con redes neuronales geométricas (GNN), por ejemplo, para la clasificación del período de aquellas tablillas de arcilla que se encuentran entre los documentos más antiguos de la historia humana. ^{[148] [149]}

Sintonia FINA

Para muchas aplicaciones, los datos de entrenamiento no están muy disponibles. Las redes neuronales convolucionales suelen requerir una gran cantidad de datos de entrenamiento para evitar el sobreajuste . Una técnica común es entrenar la red con un conjunto de datos más grande de un dominio relacionado. Una vez que los parámetros de la red han convergido, se realiza un paso de entrenamiento adicional utilizando los datos del dominio para ajustar los pesos de la red; esto se conoce como aprendizaje por transferencia . Además, esta técnica permite que las arquitecturas de redes convolucionales se apliquen con éxito a problemas con conjuntos de entrenamiento pequeños. ^[150]

Explicaciones interpretables por los humanos

El entrenamiento y la predicción de extremo a extremo son prácticas comunes en la visión artificial . Sin embargo, se requieren explicaciones interpretables por humanos para sistemas críticos como los automóviles autónomos . ^[151] Con los avances recientes en prominencia visual , atención espacial y atención temporal , las regiones espaciales/instantes temporales más críticos podrían visualizarse para justificar las predicciones de CNN. ^{[152] [153]}

Arquitecturas relacionadas

Redes Q profundas

Una red Q profunda (DQN) es un tipo de modelo de aprendizaje profundo que combina una red neuronal profunda con aprendizaje Q , una forma de aprendizaje de refuerzo . A diferencia de los agentes de aprendizaje de refuerzo anteriores, las DQN que utilizan CNN pueden aprender directamente de las entradas sensoriales de alta dimensión a través del aprendizaje de refuerzo. ^[154]

Los resultados preliminares se presentaron en 2014, con un artículo adjunto en febrero de 2015. ^[155] La investigación describió una aplicación para los juegos de Atari 2600. Otros modelos de aprendizaje de refuerzo profundo la precedieron. ^[156]

Redes de creencias profundas

Las redes convolucionales de creencias profundas (CDBN) tienen una estructura muy similar a las redes neuronales convolucionales y se entrenan de manera similar a las redes de creencias profundas. Por lo tanto, explotan la estructura 2D de las imágenes, como lo hacen las CNN, y hacen uso del preentrenamiento como las redes de creencias profundas . Proporcionan una estructura genérica que se puede utilizar en muchas tareas de procesamiento de imágenes y señales. Se han obtenido resultados de referencia en conjuntos de datos de imágenes estándar como CIFAR ^{[157] utilizando CDBN. [158]}

Pirámide de abstracción neuronal

Pirámide de abstracción neuronal

La arquitectura de retroalimentación de las redes neuronales convolucionales se extendió en la pirámide de abstracción neuronal ^[159] mediante conexiones laterales y de retroalimentación. La red convolucional recurrente resultante permite la incorporación flexible de información contextual para resolver iterativamente ambigüedades locales. A diferencia de los modelos anteriores, se generaron salidas similares a imágenes con la resolución más alta, por ejemplo, para tareas de segmentación semántica, reconstrucción de imágenes y localización de objetos.

Bibliotecas notables

• Caffe : biblioteca para redes neuronales convolucionales. Creada por el Berkeley Vision and Learning Center (BVLC). Admite CPU y GPU. Desarrollada en C++ y con contenedores para Python y MATLAB .
• Deeplearning4j : aprendizaje profundo en Java y Scala en Spark habilitado para múltiples GPU . Una biblioteca de aprendizaje profundo de propósito general para la pila de producción de JVM que se ejecuta en un motor de computación científica C++. Permite la creación de capas personalizadas. Se integra con Hadoop y Kafka.
• Dlib : un kit de herramientas para crear aplicaciones de análisis de datos y aprendizaje automático del mundo real en C++.
• Microsoft Cognitive Toolkit : un kit de herramientas de aprendizaje profundo escrito por Microsoft con varias características únicas que mejoran la escalabilidad en múltiples nodos. Admite interfaces completas para capacitación en C++ y Python y con soporte adicional para inferencia de modelos en C# y Java.
• TensorFlow : biblioteca similar a Theano con licencia Apache 2.0 con soporte para CPU, GPU, unidad de procesamiento tensorial (TPU) patentada de Google, ^[160] y dispositivos móviles.
• Theano : la biblioteca de referencia de aprendizaje profundo para Python con una API compatible en gran medida con la popular biblioteca NumPy . Permite al usuario escribir expresiones matemáticas simbólicas y luego genera automáticamente sus derivadas, lo que le ahorra al usuario tener que codificar gradientes o retropropagación. Estas expresiones simbólicas se compilan automáticamente en código CUDA para una implementación rápida en la GPU .
• Torch : un marco de computación científica con amplio soporte para algoritmos de aprendizaje automático, escrito en C y Lua .

Véase también

• Atención (aprendizaje automático)
• Circunvolución
• Aprendizaje profundo
• Procesamiento del lenguaje natural
• Neocognitrón
• Transformación de características invariantes de escala
• Red neuronal con retardo temporal
• Unidad de procesamiento de visión

Notas

1. Cuando se aplica a otros tipos de datos que no sean datos de imágenes, como datos de sonido, la "posición espacial" puede corresponder de diversas formas a diferentes puntos en el dominio del tiempo , el dominio de la frecuencia u otros espacios matemáticos .
2. De ahí el nombre "capa convolucional"
3. Los llamados datos categóricos .

Referencias

1. LeCun, Yann; Bengio, Yoshua; Hinton, Geoffrey (28 de mayo de 2015). "Aprendizaje profundo". Nature . 521 (7553): 436–444. Código Bibliográfico :2015Natur.521..436L. doi :10.1038/nature14539. ISSN  1476-4687. PMID  26017442.
2. Venkatesan, Ragav; Li, Baoxin (23 de octubre de 2017). Redes neuronales convolucionales en computación visual: una guía concisa. CRC Press. ISBN 978-1-351-65032-8Archivado desde el original el 16 de octubre de 2023. Consultado el 13 de diciembre de 2020 .
3. Balas, Valentina E.; Kumar, Raghvendra; Srivastava, Rajshree (19 de noviembre de 2019). Tendencias y avances recientes en inteligencia artificial e Internet de las cosas. Springer Nature. ISBN 978-3-030-32644-9Archivado desde el original el 16 de octubre de 2023. Consultado el 13 de diciembre de 2020 .
4. Zhang, Yingjie; Soon, Hong Geok; Ye, Dongsen; Fuh, Jerry Ying Hsi; Zhu, Kunpeng (septiembre de 2020). "Monitoreo del proceso de fusión de lecho de polvo mediante visión artificial con redes neuronales convolucionales híbridas". IEEE Transactions on Industrial Informatics . 16 (9): 5769–5779. doi :10.1109/TII.2019.2956078. ISSN  1941-0050. S2CID  213010088. Archivado desde el original el 2023-07-31 . Consultado el 2023-08-12 .
5. Chervyakov, NI; Lyakhov, PA; Deryabin, MA; Nagornov, NN; Valueva, MV; Valuev, GV (septiembre de 2020). "Solución basada en sistema de número de residuos para reducir el costo de hardware de una red neuronal convolucional". Neurocomputing . 407 : 439–453. doi :10.1016/j.neucom.2020.04.018. S2CID  219470398. Archivado desde el original el 2023-06-29 . Consultado el 2023-08-12 . Las redes neuronales convolucionales representan arquitecturas de aprendizaje profundo que se utilizan actualmente en una amplia gama de aplicaciones, incluidas la visión artificial, el reconocimiento de voz, la detección de malware, el análisis de series temporales en finanzas y muchas otras.
6. Habibi, Aghdam, Hamed (30 de mayo de 2017). Guía de redes neuronales convolucionales: una aplicación práctica para la detección y clasificación de señales de tráfico . Heravi, Elnaz Jahani. Cham, Suiza. ISBN 9783319575490.OCLC 987790957  .{{cite book}}: CS1 maint: location missing publisher (link) CS1 maint: multiple names: authors list (link)
7. Homma, Toshiteru; Les Atlas; Robert Marks II (1987). "Una red neuronal artificial para patrones bipolares espacio-temporales: aplicación a la clasificación de fonemas" (PDF) . Avances en sistemas de procesamiento de información neuronal . 1 : 31–40. Archivado (PDF) desde el original el 2022-03-31 . Consultado el 2022-03-31 . La noción de convolución o correlación utilizada en los modelos presentados es popular en las disciplinas de ingeniería y se ha aplicado ampliamente al diseño de filtros, sistemas de control, etc.
8. Valueva, MV; Nagornov, NN; Lyakhov, PA; Valuev, GV; Chervyakov, NI (2020). "Aplicación del sistema de números de residuos para reducir los costos de hardware de la implementación de la red neuronal convolucional". Matemáticas y computadoras en simulación . 177 . Elsevier BV: 232–243. doi :10.1016/j.matcom.2020.04.031. ISSN  0378-4754. S2CID  218955622. Las redes neuronales convolucionales son una herramienta prometedora para resolver el problema del reconocimiento de patrones.
9. van den Oord, Aarón; Dieleman, Sander; Schrauwen, Benjamín (1 de enero de 2013). Burges, CJC; Bottou, L.; Bien, M.; Ghahramani, Z.; Weinberger, KQ (eds.). Recomendación musical profunda basada en contenido (PDF) . Curran Associates, Inc. págs. 2643–2651. Archivado (PDF) desde el original el 7 de marzo de 2022 . Consultado el 31 de marzo de 2022 .
10. Collobert, Ronan; Weston, Jason (1 de enero de 2008). "Una arquitectura unificada para el procesamiento del lenguaje natural". Actas de la 25.ª conferencia internacional sobre aprendizaje automático - ICML '08 . Nueva York, NY, EE. UU.: ACM. págs. 160–167. doi :10.1145/1390156.1390177. ISBN 978-1-60558-205-4. Número de identificación del sujeto  2617020.
11. Avilov, Oleksii; Rimbert, Sebastien; Popov, Anton; Bougrain, Laurent (julio de 2020). "Técnicas de aprendizaje profundo para mejorar la detección de la conciencia intraoperatoria a partir de señales electroencefalográficas". 42.ª Conferencia internacional anual de 2020 de la IEEE Engineering in Medicine & Biology Society (EMBC) (PDF) . Vol. 2020. Montreal, QC, Canadá: IEEE. págs. 142–145. doi :10.1109/EMBC44109.2020.9176228. ISBN . 978-1-7281-1990-8. PMID  33017950. S2CID  221386616. Archivado (PDF) del original el 2022-05-19 . Consultado el 2023-07-21 .
12. Tsantekidis, Avraam; Passalis, Nikolaos; Tefas, Anastasios; Kanniainen, Juho; Gabbouj, Moncef; Iosifidis, Alexandros (julio de 2017). "Previsión de precios de acciones a partir del libro de órdenes limitadas mediante redes neuronales convolucionales". 2017 IEEE 19th Conference on Business Informatics (CBI) . Tesalónica, Grecia: IEEE. págs. 7–12. doi :10.1109/CBI.2017.23. ISBN 978-1-5386-3035-8.S2CID 4950757  .
13. Zhang, Wei (1988). "Red neuronal de reconocimiento de patrones invariante al cambio y su arquitectura óptica". Actas de la Conferencia Anual de la Sociedad Japonesa de Física Aplicada . Archivado desde el original el 23 de junio de 2020. Consultado el 22 de junio de 2020 .
14. Zhang, Wei (1990). "Modelo de procesamiento distribuido paralelo con interconexiones locales invariantes en el espacio y su arquitectura óptica". Óptica Aplicada . 29 (32): 4790–7. Código Bibliográfico :1990ApOpt..29.4790Z. doi :10.1364/AO.29.004790. PMID  20577468. Archivado desde el original el 2017-02-06 . Consultado el 2016-09-22 .
15. Mouton, Coenraad; Myburgh, Johannes C.; Davel, Marelie H. (2020). "Invariancia de paso y traslación en CNN". En Gerber, Aurona (ed.). Investigación en inteligencia artificial . Comunicaciones en informática y ciencias de la información. Vol. 1342. Cham: Springer International Publishing. págs. 267–281. arXiv : 2103.10097 . doi :10.1007/978-3-030-66151-9_17. ISBN 978-3-030-66151-9. S2CID  232269854. Archivado desde el original el 27 de junio de 2021. Consultado el 26 de marzo de 2021 .
16. Kurtzman, Thomas (20 de agosto de 2019). "El sesgo oculto en el conjunto de datos DUD-E conduce a un rendimiento engañoso del aprendizaje profundo en el cribado virtual basado en la estructura". PLOS ONE . ​​14 (8): e0220113. Bibcode :2019PLoSO..1420113C. doi : 10.1371/journal.pone.0220113 . PMC 6701836 . PMID  31430292. 
17. Fukushima, K. (2007). "Neocognitron". Scholarpedia . 2 (1): 1717. Bibcode :2007SchpJ...2.1717F. doi : 10.4249/scholarpedia.1717 .
18. Hubel, DH; Wiesel, TN (1968-03-01). "Campos receptivos y arquitectura funcional de la corteza estriada del mono". The Journal of Physiology . 195 (1): 215–243. doi :10.1113/jphysiol.1968.sp008455. ISSN  0022-3751. PMC 1557912 . PMID  4966457. 
19. Fukushima, Kunihiko (1980). "Neocognitron: A Self-organizing Neural Network Model for a Mechanism of Pattern Recognition Unaffected by Shift in Position" (PDF) . Cibernética biológica . 36 (4): 193–202. doi :10.1007/BF00344251. PMID  7370364. S2CID  206775608. Archivado (PDF) desde el original el 3 de junio de 2014 . Consultado el 16 de noviembre de 2013 .
20. Matusugu, Masakazu; Katsuhiko Mori; Yusuke Mitari; Yuji Kaneda (2003). "Reconocimiento de expresiones faciales independiente del sujeto con detección robusta de rostros utilizando una red neuronal convolucional" (PDF) . Redes neuronales . 16 (5): 555–559. doi :10.1016/S0893-6080(03)00115-1. PMID  12850007. Archivado (PDF) desde el original el 13 de diciembre de 2013 . Consultado el 17 de noviembre de 2013 .
21. Redes neuronales convolucionales desmitificadas: un tutorial basado en la perspectiva del filtrado combinado https://arxiv.org/abs/2108.11663v3
22. "Redes neuronales convolucionales (LeNet) – Documentación de DeepLearning 0.1". DeepLearning 0.1 . LISA Lab. Archivado desde el original el 28 de diciembre de 2017 . Consultado el 31 de agosto de 2013 .
23. Chollet, François (4 de abril de 2017). "Xception: aprendizaje profundo con convoluciones separables en profundidad". arXiv : 1610.02357 [cs.CV].
24. Ciresan, Dan; Ueli Meier; Jonathan Masci; Luca M. Gambardella; Jurgen Schmidhuber (2011). "Redes neuronales convolucionales flexibles y de alto rendimiento para la clasificación de imágenes" (PDF) . Actas de la vigésimo segunda conferencia conjunta internacional sobre inteligencia artificial, volumen dos . 2 : 1237–1242. Archivado (PDF) desde el original el 5 de abril de 2022 . Consultado el 17 de noviembre de 2013 .
25. Krizhevsky , Alex. «Clasificación ImageNet con redes neuronales convolucionales profundas» (PDF) . Archivado (PDF) del original el 25 de abril de 2021. Consultado el 17 de noviembre de 2013 .
26. Yamaguchi, Kouichi; Sakamoto, Kenji; Akabane, Toshio; Fujimoto, Yoshiji (noviembre de 1990). Una red neuronal para el reconocimiento de palabras aisladas independiente del hablante. Primera Conferencia Internacional sobre Procesamiento del Lenguaje Hablado (ICSLP 90). Kobe, Japón. Archivado desde el original el 2021-03-07 . Consultado el 2019-09-04 .
27. Ciresan, Dan; Meier, Ueli; Schmidhuber, Jürgen (junio de 2012). "Redes neuronales profundas de múltiples columnas para la clasificación de imágenes". Conferencia IEEE de 2012 sobre visión artificial y reconocimiento de patrones . Nueva York, NY: Instituto de Ingenieros Eléctricos y Electrónicos (IEEE). págs. 3642–3649. arXiv : 1202.2745 . CiteSeerX 10.1.1.300.3283 . doi :10.1109/CVPR.2012.6248110. ISBN  978-1-4673-1226-4. OCLC  812295155. S2CID  2161592.
28. Yu, Fisher; Koltun, Vladlen (30 de abril de 2016). "Agregación de contexto multiescala mediante convoluciones dilatadas". arXiv : 1511.07122 [cs.CV].
29. Chen, Liang-Chieh; Papandreou, George; Schroff, Florian; Adam, Hartwig (5 de diciembre de 2017). "Replanteamiento de la convolución atrosa para la segmentación semántica de imágenes". arXiv : 1706.05587 [cs.CV].
30. Duta, Ionut Cosmin; Georgescu, Mariana Juliana; Ionescu, Radu Tudor (16 de agosto de 2021). "Redes neuronales convolucionales contextuales". arXiv : 2108.07387 [cs.CV].
31. LeCun, Yann. «LeNet-5, redes neuronales convolucionales». Archivado desde el original el 24 de febrero de 2021. Consultado el 16 de noviembre de 2013 .
32. Zeiler, Matthew D.; Taylor, Graham W.; Fergus, Rob (noviembre de 2011). "Redes deconvolucionales adaptativas para el aprendizaje de características de nivel medio y alto". Conferencia internacional sobre visión artificial de 2011. IEEE. págs. 2018–2025. doi :10.1109/iccv.2011.6126474. ISBN . 978-1-4577-1102-2.
33. Dumoulin, Vincent; Visin, Francesco (11 de enero de 2018), Una guía para la aritmética de convolución para el aprendizaje profundo , arXiv : 1603.07285
34. Ódena, Augusto; Dumoulin, Vicente; Olah, Chris (17 de octubre de 2016). "Artefactos de deconvolución y tablero de ajedrez". Destilar . 1 (10): e3. doi : 10.23915/distill.00003. ISSN  2476-0757.
35. van Dyck, Leonard Elia; Kwitt, Roland; Denzler, Sebastian Jochen; Gruber, Walter Roland (2021). "Comparación del reconocimiento de objetos en humanos y redes neuronales convolucionales profundas: un estudio de seguimiento ocular". Frontiers in Neuroscience . 15 : 750639. doi : 10.3389/fnins.2021.750639 . ISSN  1662-453X. PMC 8526843 . PMID  34690686. 
36. Hubel, DH; Wiesel, TN (octubre de 1959). "Campos receptivos de neuronas individuales en la corteza estriada del gato". J. Physiol . 148 (3): 574–91. doi :10.1113/jphysiol.1959.sp006308. PMC 1363130 . PMID  14403679. 
37. David H. Hubel y Torsten N. Wiesel (2005). Cerebro y percepción visual: la historia de una colaboración de 25 años. Oxford University Press US. p. 106. ISBN 978-0-19-517618-6Archivado desde el original el 16 de octubre de 2023. Consultado el 18 de enero de 2019 .
38. Fukushima, K. (1969). "Extracción de características visuales mediante una red multicapa de elementos de umbral analógicos". IEEE Transactions on Systems Science and Cybernetics . 5 (4): 322–333. doi :10.1109/TSSC.1969.300225.
39. Ramachandran, Prajit; Barret, Zoph; Quoc, V. Le (16 de octubre de 2017). "Búsqueda de funciones de activación". arXiv : 1710.05941 [cs.NE].
40. Fukushima, Kunihiko (octubre de 1979). "位置ずれに影響されないパターン認識機構の神経回路のモデル --- ネオコグニトロン ---" [Modelo de red neuronal para un mecanismo de reconocimiento de patrones que no se ve afectado por el cambio de posición - Neocognitron -]. Trans. IECE (en japonés). J62-A (10): 658–665.
41. Weng, J; Ahuja, N; Huang, TS (1993). "Aprendizaje del reconocimiento y segmentación de objetos 3-D a partir de imágenes 2-D". 1993 (4.ª) Conferencia Internacional sobre Visión por Computador . IEEE. págs. 121–128. doi :10.1109/ICCV.1993.378228. ISBN. 0-8186-3870-2.S2CID8619176  .​
42. Schmidhuber, Jürgen (2015). "Aprendizaje profundo". Scholarpedia . 10 (11): 1527–54. CiteSeerX 10.1.1.76.1541 . doi :10.1162/neco.2006.18.7.1527. PMID  16764513. S2CID  2309950. Archivado desde el original el 19 de abril de 2016 . Consultado el 20 de enero de 2019 . 
43. Waibel, Alex (diciembre de 1987). Reconocimiento de fonemas mediante redes neuronales con retardo temporal (PDF) . Reunión del Instituto de Ingenieros Eléctricos, de Información y de Comunicaciones (IEICE). Tokio, Japón.
44. Alexander Waibel et al., Reconocimiento de fonemas mediante redes neuronales con retardo temporal Archivado el 25 de febrero de 2021 en Wayback Machine. IEEE Transactions on Acoustics, Speech, and Signal Processing, Volumen 37, N.º 3, págs. 328. - 339, marzo de 1989.
45. LeCun, Yann; Bengio, Yoshua (1995). "Convolutional networks for images, speech, and time series" (Redes convolucionales para imágenes, habla y series temporales). En Arbib, Michael A. (ed.). The handbook of brain theory and neural networks (Segunda ed.). The MIT press. págs. 276–278. Archivado desde el original el 28 de julio de 2020. Consultado el 3 de diciembre de 2019 .
46. John B. Hampshire y Alexander Waibel, Arquitecturas conexionistas para el reconocimiento de fonemas de múltiples hablantes Archivado el 31 de marzo de 2022 en Wayback Machine , Avances en sistemas de procesamiento de información neuronal, 1990, Morgan Kaufmann.
47. Ko, Tom; Peddinti, Vijayaditya; Povey, Daniel; Seltzer, Michael L.; Khudanpur, Sanjeev (marzo de 2018). Un estudio sobre el aumento de datos del habla reverberante para el reconocimiento de voz robusto (PDF) . 42.ª Conferencia internacional IEEE sobre acústica, habla y procesamiento de señales (ICASSP 2017). Nueva Orleans, LA, EE. UU. Archivado (PDF) desde el original el 8 de julio de 2018. Consultado el 4 de septiembre de 2019 .
48. Denker, JS, Gardner, WR, Graf, H. P, Henderson, D, Howard, RE, Hubbard, W, Jackel, LD, BaIrd, HS y Guyon (1989) Reconocedor de red neuronal para dígitos de códigos postales escritos a mano Archivado el 4 de agosto de 2018 en Wayback Machine , AT&T Bell Laboratories
49. Y. LeCun, B. Boser, JS Denker, D. Henderson, RE Howard, W. Hubbard, LD Jackel, Retropropagación aplicada al reconocimiento de códigos postales escritos a mano Archivado el 10 de enero de 2020 en Wayback Machine ; AT&T Bell Laboratories
50. Zhang, Wei (1991). "Procesamiento de imágenes del endotelio corneal humano basado en una red de aprendizaje". Applied Optics . 30 (29): 4211–7. Bibcode :1991ApOpt..30.4211Z. doi :10.1364/AO.30.004211. PMID  20706526. Archivado desde el original el 2017-02-06 . Consultado el 2016-09-22 .
51. Zhang, Wei (1994). "Detección computarizada de microcalcificaciones agrupadas en mamografías digitales utilizando una red neuronal artificial invariante al cambio". Medical Physics . 21 (4): 517–24. Bibcode :1994MedPh..21..517Z. doi :10.1118/1.597177. PMID  8058017. Archivado desde el original el 2017-02-06 . Consultado el 2016-09-22 .
52. Lecun, Y.; Jackel, LD; Bottou, L.; Cortés, C.; Denker, JS; Drucker, H.; Guyón, I.; Müller, UA; Sackinger, E.; Simard, P.; Vapnik, V. (agosto de 1995). Algoritmos de aprendizaje para la clasificación: una comparación sobre el reconocimiento de dígitos escritos a mano (PDF) . Científico mundial. págs. 261–276. doi :10.1142/2808. ISBN 978-981-02-2324-3. Archivado (PDF) del original el 2 de mayo de 2023.
53. Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. (noviembre de 1998). "Aprendizaje basado en gradientes aplicado al reconocimiento de documentos". Actas del IEEE . 86 (11): 2278–2324. doi :10.1109/5.726791.
54. Zhang, Wei (1991). "Error Back Propagation with Minimum-Entropy Weights: A Technique for Better Generalization of 2-D Shift-Invariant NNs" (Propagación de errores con pesos de entropía mínima: una técnica para una mejor generalización de redes neuronales invariantes en 2 dimensiones). Actas de la Conferencia conjunta internacional sobre redes neuronales . Archivado desde el original el 6 de febrero de 2017. Consultado el 22 de septiembre de 2016 .
55. Daniel Graupe, Ruey Wen Liu, George S Moschytz."Aplicaciones de redes neuronales al procesamiento de señales médicas Archivado el 28 de julio de 2020 en Wayback Machine ". En Proc. 27th IEEE Decision and Control Conf., págs. 343–347, 1988.
56. Daniel Graupe, Boris Vern, G. Gruener, Aaron Field y Qiu Huang. "Descomposición de señales EMG de superficie en potenciales de acción de fibra única mediante redes neuronales Archivado el 4 de septiembre de 2019 en Wayback Machine ". Proc. Simposio Internacional IEEE sobre Circuitos y Sistemas, págs. 1008–1011, 1989.
57. Qiu Huang, Daniel Graupe, Yi Fang Huang, Ruey Wen Liu."Identificación de patrones de activación de señales neuronales ^{[ vínculo muerto ]} ". En Proc. 28th IEEE Decision and Control Conf., págs. 266–271, 1989. https://ieeexplore.ieee.org/document/70115 Archivado el 31 de marzo de 2022 en Wayback Machine.
58. Oh, KS; Jung, K (2004). "Implementación de redes neuronales mediante GPU". Reconocimiento de patrones . 37 (6): 1311–1314. Código Bibliográfico :2004PatRe..37.1311O. doi :10.1016/j.patcog.2004.01.013.
59. Dave Steinkraus; Patrice Simard; Ian Buck (2005). "Uso de GPU para algoritmos de aprendizaje automático". 12.ª Conferencia internacional sobre análisis y reconocimiento de documentos (ICDAR 2005) . págs. 1115–1119. doi :10.1109/ICDAR.2005.251. Archivado desde el original el 2022-03-31 . Consultado el 2022-03-31 .
60. Kumar Chellapilla; Sid Puri; Patrice Simard (2006). "Redes neuronales convolucionales de alto rendimiento para el procesamiento de documentos". En Lorette, Guy (ed.). Décimo taller internacional sobre fronteras en el reconocimiento de escritura a mano . Suvisoft. Archivado desde el original el 2020-05-18 . Consultado el 2016-03-14 .
61. Hinton, GE; Osindero, S; Teh, YW (julio de 2006). "Un algoritmo de aprendizaje rápido para redes de creencias profundas". Neural Computation . 18 (7): 1527–54. CiteSeerX 10.1.1.76.1541 . doi :10.1162/neco.2006.18.7.1527. PMID  16764513. S2CID  2309950. 
62. Bengio, Yoshua; Lamblin, Pascal; Popovici, Dan; Larochelle, Hugo (2007). "Entrenamiento voraz por capas de redes profundas" (PDF) . Avances en sistemas de procesamiento de información neuronal : 153–160. Archivado (PDF) desde el original el 2 de junio de 2022 . Consultado el 31 de marzo de 2022 .
63. Ranzato, MarcAurelio; Poultney, Christopher; Chopra, Sumit; LeCun, Yann (2007). "Aprendizaje eficiente de representaciones dispersas con un modelo basado en energía" (PDF) . Avances en sistemas de procesamiento de información neuronal . Archivado (PDF) desde el original el 22 de marzo de 2016 . Consultado el 26 de junio de 2014 .
64. Raina, R; Madhavan, A; Ng, Andrew (14 de junio de 2009). "Aprendizaje profundo no supervisado a gran escala utilizando procesadores gráficos" (PDF) . Actas de la 26.ª Conferencia Internacional Anual sobre Aprendizaje Automático . ICML '09: Actas de la 26.ª Conferencia Internacional Anual sobre Aprendizaje Automático. págs. 873–880. doi :10.1145/1553374.1553486. ISBN 9781605585161. S2CID  392458. Archivado (PDF) del original el 8 de diciembre de 2020 . Consultado el 22 de diciembre de 2023 .
65. Ciresan, Dan; Meier, Ueli; Gambardella, Luca; Schmidhuber, Jürgen (2010). "Redes neuronales grandes y simples para el reconocimiento de dígitos escritos a mano". Neural Computation . 22 (12): 3207–3220. arXiv : 1003.0358 . doi :10.1162/NECO_a_00052. PMID  20858131. S2CID  1918673.
66. "Tabla de resultados de la competición IJCNN 2011". COMPETICIÓN OFICIAL IJCNN2011 . 2010. Archivado desde el original el 2021-01-17 . Consultado el 2019-01-14 .
67. Schmidhuber, Jürgen (17 de marzo de 2017). «Historia de los concursos de visión artificial ganados por las CNN profundas en la GPU». Archivado desde el original el 19 de diciembre de 2018. Consultado el 14 de enero de 2019 .
68. Krizhevsky, Alex; Sutskever, Ilya; Hinton, Geoffrey E. (24 de mayo de 2017). "Clasificación ImageNet con redes neuronales convolucionales profundas" (PDF) . Comunicaciones de la ACM . 60 (6): 84–90. doi :10.1145/3065386. ISSN  0001-0782. S2CID  195908774. Archivado (PDF) desde el original el 16 de mayo de 2017 . Consultado el 4 de diciembre de 2018 .
69. Viebke, Andre; Memeti, Suejb; Pllana, Sabri; Abraham, Ajith (2019). "CHAOS: un esquema de paralelización para entrenar redes neuronales convolucionales en Intel Xeon Phi". The Journal of Supercomputing . 75 (1): 197–227. arXiv : 1702.07908 . doi :10.1007/s11227-017-1994-x. S2CID  14135321.
70. Viebke, Andre; Pllana, Sabri (2015). "El potencial de Intel (R) Xeon Phi para el aprendizaje profundo supervisado". 2015 IEEE 17th International Conference on High Performance Computing and Communications, 2015 IEEE 7th International Symposium on Cyberspace Safety and Security, y 2015 IEEE 12th International Conference on Embedded Software and Systems . IEEE Xplore . IEEE 2015. págs. 758–765. doi :10.1109/HPCC-CSS-ICESS.2015.45. ISBN 978-1-4799-8937-9. S2CID  15411954. Archivado desde el original el 6 de marzo de 2023. Consultado el 31 de marzo de 2022 .
71. Hinton, Geoffrey (2012). «Clasificación ImageNet con redes neuronales convolucionales profundas». NIPS'12: Actas de la 25.ª Conferencia internacional sobre sistemas de procesamiento de información neuronal - Volumen 1. 1 : 1097–1105. Archivado desde el original el 2019-12-20 . Consultado el 26 de marzo de 2021 – vía ACM.
72. Azulay, Aharon; Weiss, Yair (2019). "¿Por qué las redes convolucionales profundas se generalizan tan mal a transformaciones de imágenes pequeñas?". Journal of Machine Learning Research . 20 (184): 1–25. ISSN  1533-7928. Archivado desde el original el 2022-03-31 . Consultado el 2022-03-31 .
73. Géron, Aurélien (2019). Aprendizaje automático práctico con Scikit-Learn, Keras y TensorFlow . Sebastopol, CA: O'Reilly Media. ISBN 978-1-492-03264-9., pág. 448
74. "CS231n Redes neuronales convolucionales para reconocimiento visual". cs231n.github.io . Archivado desde el original el 23 de octubre de 2019 . Consultado el 25 de abril de 2017 .
75. Nirthika, Rajendran; Manivannan, Siyamalan; Ramanan, Amirthalingam; Wang, Ruixuan (1 de abril de 2022). "Agrupamiento en redes neuronales convolucionales para el análisis de imágenes médicas: una encuesta y un estudio empírico". Computación neuronal y aplicaciones . 34 (7): 5321–5347. doi :10.1007/s00521-022-06953-8. ISSN  1433-3058. PMC 8804673 . PMID  35125669. 
76. Scherer, Dominik; Müller, Andreas C.; Behnke, Sven (2010). "Evaluation of Pooling Operations in Convolutional Architectures for Object Recognition" (PDF) . Redes neuronales artificiales (ICANN), 20.ª conferencia internacional sobre . Tesalónica, Grecia: Springer. págs. 92–101. Archivado (PDF) desde el original el 2018-04-03 . Consultado el 2016-12-28 .
77. Graham, Benjamin (18 de diciembre de 2014). "Agrupamiento máximo fraccional". arXiv : 1412.6071 [cs.CV].
78. Springenberg, Jost Tobias; Dosovitskiy, Alexey; Brox, Thomas; Riedmiller, Martin (21 de diciembre de 2014). "En busca de la simplicidad: la red totalmente convolucional". arXiv : 1412.6806 [cs.LG].
79. Ma, Zhanyu; Chang, Dongliang; Xie, Jiyang; Ding, Yifeng; Wen, Shaoguo; Li, Xiaoxu; Si, Zhongwei; Guo, Jun (2019). "Clasificación de vehículos de grano fino con CNN modificadas con agrupación máxima de canales". Transacciones IEEE sobre tecnología vehicular . 68 (4). Instituto de Ingenieros Eléctricos y Electrónicos (IEEE): 3224–3233. doi :10.1109/tvt.2019.2899972. ISSN  0018-9545. S2CID  86674074.
80. Zafar, Afia; Aamir, Muhammad; Mohd Nawi, Nazri; Arshad, Ali; Riaz, Saman; Alruban, Abdulrahman; Dutta, Ashit Kumar; Almotairi, Sultan (2022-08-29). "Una comparación de métodos de agrupamiento para redes neuronales convolucionales". Applied Sciences . 12 (17): 8643. doi : 10.3390/app12178643 . ISSN  2076-3417.
81. Gholamalinezhad, Hossein; Khosravi, Hossein (16 de septiembre de 2020), Métodos de agrupación en redes neuronales profundas, una revisión , arXiv : 2009.07485
82. Householder, Alston S. (junio de 1941). "Una teoría de la actividad en estado estacionario en redes de fibras nerviosas: I. Definiciones y lemas preliminares". Boletín de biofísica matemática . 3 (2): 63–69. doi :10.1007/BF02478220. ISSN  0007-4985.
83. Romanuke, Vadim (2017). "Número apropiado y asignación de ReLU en redes neuronales convolucionales". Boletín de investigación de NTUU "Instituto Politécnico de Kiev" . 1 (1): 69–78. doi : 10.20535/1810-0546.2017.1.88156 .
84. Xavier Glorot; Antoine Bordes; Yoshua Bengio (2011). Redes neuronales rectificadoras dispersas profundas (PDF) . AISTATS. Archivado desde el original (PDF) el 2016-12-13 . Consultado el 2023-04-10 . Funciones de activación de rectificador y softplus. La segunda es una versión suave de la primera.
85. Krizhevsky, A.; Sutskever, I.; Hinton, GE (2012). "Clasificación de imagenet con redes neuronales convolucionales profundas" (PDF) . Avances en sistemas de procesamiento de información neuronal . 1 : 1097–1105. Archivado (PDF) desde el original el 2022-03-31 . Consultado el 2022-03-31 .
86. Ribeiro, Antonio H.; Schön, Thomas B. (2021). "Cómo las redes neuronales convolucionales se enfrentan al aliasing". ICASSP 2021 - 2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) . págs. 2755–2759. arXiv : 2102.07757 . doi :10.1109/ICASSP39728.2021.9414627. ISBN 978-1-7281-7605-5. Número de identificación del sujeto  231925012.
87. Myburgh, Johannes C.; Mouton, Coenraad; Davel, Marelie H. (2020). "Seguimiento de la invariancia de la traducción en CNNS". En Gerber, Aurona (ed.). Investigación en inteligencia artificial . Comunicaciones en informática y ciencias de la información. Vol. 1342. Cham: Springer International Publishing. págs. 282–295. arXiv : 2104.05997 . doi :10.1007/978-3-030-66151-9_18. ISBN . 978-3-030-66151-9. S2CID  233219976. Archivado desde el original el 22 de enero de 2022. Consultado el 26 de marzo de 2021 .
88. Richard, Zhang (25 de abril de 2019). Cómo hacer que las redes convolucionales vuelvan a ser invariantes respecto del cambio. OCLC  1106340711.
89. Jadeberg, Simonyan, Zisserman, Kavukcuoglu, Max, Karen, Andrew, Koray (2015). "Redes de transformadores espaciales" (PDF) . Avances en sistemas de procesamiento de información neuronal . 28 . Archivado (PDF) desde el original el 2021-07-25 . Consultado el 2021-03-26 – vía NIPS.{{cite journal}}: CS1 maint: multiple names: authors list (link)
90. E, Sabour, Sara Frosst, Nicholas Hinton, Geoffrey (26 de octubre de 2017). Enrutamiento dinámico entre cápsulas. OCLC  1106278545.{{cite book}}: CS1 maint: multiple names: authors list (link)
91. Matiz, Sergio; Barner, Kenneth E. (1 de junio de 2019). "Predictor conformal inductivo para redes neuronales convolucionales: aplicaciones al aprendizaje activo para la clasificación de imágenes". Reconocimiento de patrones . 90 : 172–182. Código Bibliográfico :2019PatRe..90..172M. doi :10.1016/j.patcog.2019.01.035. ISSN  0031-3203. S2CID  127253432. Archivado desde el original el 29 de septiembre de 2021 . Consultado el 29 de septiembre de 2021 .
92. Wieslander, Håkan; Harrison, Philip J.; Skogberg, Gabriel; Jackson, Sonya; Fridén, Markus; Karlsson, Johan; Spjuth, Ola; Wählby, Carolina (febrero de 2021). "Aprendizaje profundo con predicción conforme para el análisis jerárquico de imágenes de tejido de portaobjetos completo a gran escala". Revista IEEE de informática biomédica y sanitaria . 25 (2): 371–380. doi : 10.1109/JBHI.2020.2996300 . ISSN  2168-2208. PMID  32750907. S2CID  219885788.
93. Srivastava, Nitish; C. Geoffrey Hinton; Alex Krizhevsky; Ilya Sutskever; Ruslan Salakhutdinov (2014). "Dropout: A Simple Way to Prevent Neural Networks from Overfitting" (PDF) . Revista de investigación en aprendizaje automático . 15 (1): 1929–1958. Archivado (PDF) desde el original el 19 de enero de 2016 . Consultado el 3 de enero de 2015 .
94. "Regularización de redes neuronales mediante DropConnect | ICML 2013 | JMLR W&CP". jmlr.org : 1058–1066. 13 de febrero de 2013. Archivado desde el original el 12 de agosto de 2017. Consultado el 17 de diciembre de 2015 .
95. Zeiler, Matthew D.; Fergus, Rob (15 de enero de 2013). "Agrupamiento estocástico para la regularización de redes neuronales convolucionales profundas". arXiv : 1301.3557 [cs.LG].
96. Platt, John; Steinkraus, Dave; Simard, Patrice Y. (agosto de 2003). "Mejores prácticas para redes neuronales convolucionales aplicadas al análisis visual de documentos – Microsoft Research". Microsoft Research . Archivado desde el original el 2017-11-07 . Consultado el 2015-12-17 .
97. Hinton, Geoffrey E.; Srivastava, Nitish; Krizhevsky, Alex; Sutskever, Ilya; Salakhutdinov, Ruslan R. (2012). "Mejora de las redes neuronales mediante la prevención de la coadaptación de los detectores de características". arXiv : 1207.0580 [cs.NE].
98. "Dropout: A Simple Way to Prevent Neural Networks from Overfitting" (Deserción: una forma sencilla de evitar el sobreajuste de las redes neuronales). jmlr.org . Archivado desde el original el 5 de marzo de 2016. Consultado el 17 de diciembre de 2015 .
99. Hinton, Geoffrey (1979). "Algunas demostraciones de los efectos de las descripciones estructurales en las imágenes mentales". Cognitive Science . 3 (3): 231–250. doi :10.1016/s0364-0213(79)80008-7.
100. Rock, Irvin. "El marco de referencia". El legado de Solomon Asch: Ensayos sobre cognición y psicología social (1990): 243–268.
101. J. Hinton, Conferencias de Coursera sobre redes neuronales, 2012, URL: https://www.coursera.org/learn/neural-networks Archivado el 31 de diciembre de 2016 en Wayback Machine.
102. Dave Gershgorn (18 de junio de 2018). «La historia interna de cómo la IA se volvió lo suficientemente buena como para dominar Silicon Valley». Quartz . Archivado desde el original el 12 de diciembre de 2019. Consultado el 5 de octubre de 2018 .
103. Lawrence, Steve; C. Lee Giles; Ah Chung Tsoi; Andrew D. Back (1997). "Reconocimiento facial: un enfoque de red neuronal convolucional". IEEE Transactions on Neural Networks . 8 (1): 98–113. CiteSeerX 10.1.1.92.5813 . doi :10.1109/72.554195. PMID  18255614. S2CID  2883848. 
104. Le Callet, Patrick; Christian Viard-Gaudin; Dominique Barba (2006). "Un enfoque de red neuronal convolucional para la evaluación objetiva de la calidad del video" (PDF) . IEEE Transactions on Neural Networks . 17 (5): 1316–1327. doi :10.1109/TNN.2006.879766. PMID  17001990. S2CID  221185563. Archivado (PDF) del original el 24 de febrero de 2021 . Consultado el 17 de noviembre de 2013 .
105. "Concurso de reconocimiento visual a gran escala ImageNet 2014 (ILSVRC2014)". Archivado desde el original el 5 de febrero de 2016 . Consultado el 30 de enero de 2016 .
106. Szegedy, Christian; Liu, Wei; Jia, Yangqing; Sermanet, Pierre; Reed, Scott E.; Anguelov, Dragomir; Erhan, Dumitru; Vanhoucke, Vincent; Rabinovich, Andrew (2015). "Profundizando con las convoluciones". Conferencia IEEE sobre Visión artificial y reconocimiento de patrones, CVPR 2015, Boston, MA, EE. UU., 7 al 12 de junio de 2015. IEEE Computer Society. págs. 1–9. arXiv : 1409.4842 . doi :10.1109/CVPR.2015.7298594. ISBN. 978-1-4673-6964-0.
107. Rusakovsky, Olga ; Deng, Jia; Su, Hao; Krause, Jonathan; Satheesh, Sanjeev; Mamá, Sean; Huang, Zhiheng; Karpathy, Andrej ; Khosla, Aditya; Bernstein, Michael; Berg, Alejandro C.; Fei-Fei, Li (2014). "Desafío de reconocimiento visual a gran escala de Image Net ". arXiv : 1409.0575 [cs.CV].
108. "El algoritmo de detección de rostros que revolucionará la búsqueda de imágenes". Technology Review . 16 de febrero de 2015. Archivado desde el original el 20 de septiembre de 2020 . Consultado el 27 de octubre de 2017 .
109. Baccouche, Moez; Mamalet, Franck; Wolf, Christian; Garcia, Christophe; Baskurt, Atilla (16 de noviembre de 2011). "Aprendizaje profundo secuencial para el reconocimiento de acciones humanas". En Salah, Albert Ali; Lepri, Bruno (eds.). Human Behavior Unterstanding . Lecture Notes in Computer Science. Vol. 7065. Springer Berlin Heidelberg. págs. 29–39. CiteSeerX 10.1.1.385.4740 . doi :10.1007/978-3-642-25446-8_4. ISBN  978-3-642-25445-1.
110. Ji, Shuiwang; Xu, Wei; Yang, Ming; Yu, Kai (1 de enero de 2013). "Redes neuronales convolucionales 3D para el reconocimiento de acciones humanas". IEEE Transactions on Pattern Analysis and Machine Intelligence . 35 (1): 221–231. CiteSeerX 10.1.1.169.4046 . doi :10.1109/TPAMI.2012.59. ISSN  0162-8828. PMID  22392705. S2CID  1923924. 
111. Huang, Jie; Zhou, Wengang; Zhang, Qilin; Li, Houqiang; Li, Weiping (2018). "Reconocimiento de lengua de signos basado en vídeo sin segmentación temporal". arXiv : 1801.10111 [cs.CV].
112. Karpathy, Andrej, et al. "Clasificación de vídeo a gran escala con redes neuronales convolucionales Archivado el 6 de agosto de 2019 en Wayback Machine ." Conferencia IEEE sobre visión artificial y reconocimiento de patrones (CVPR). 2014.
113. Simonyan, Karen; Zisserman, Andrew (2014). "Redes convolucionales de dos flujos para el reconocimiento de acciones en vídeos". arXiv : 1406.2199 [cs.CV].(2014).
114. Wang, Le; Duan, Xuhuan; Zhang, Qilin; Niu, Zhenxing; Hua, Gang; Zheng, Nanning (22 de mayo de 2018). "Segment-Tube: localización de acciones espacio-temporales en vídeos sin recortar con segmentación por fotograma" (PDF) . Sensors . 18 (5): 1657. Bibcode :2018Senso..18.1657W. doi : 10.3390/s18051657 . ISSN  1424-8220. PMC 5982167 . PMID  29789447. Archivado (PDF) desde el original el 2021-03-01 . Consultado el 2018-09-14 . 
115. Duan, Xuhuan; Wang, Le; Zhai, Changbo; Zheng, Nanning; Zhang, Qilin; Niu, Zhenxing; Hua, pandilla (2018). "Localización conjunta de acciones espacio-temporales en vídeos sin recortar con segmentación por fotograma". 2018 25a Conferencia Internacional IEEE sobre Procesamiento de Imágenes (ICIP) . 25ª Conferencia Internacional IEEE sobre Procesamiento de Imágenes (ICIP). págs. 918–922. doi :10.1109/icip.2018.8451692. ISBN 978-1-4799-7061-2.
116. Taylor, Graham W.; Fergus, Rob; LeCun, Yann; Bregler, Christoph (1 de enero de 2010). Aprendizaje convolucional de características espacio-temporales. Actas de la 11.ª Conferencia Europea sobre Visión por Computador: Parte VI. ECCV'10. Berlín, Heidelberg: Springer-Verlag. págs. 140–153. ISBN 978-3-642-15566-6Archivado desde el original el 31-03-2022 . Consultado el 31-03-2022 .
117. Le, QV; Zou, WY; Yeung, SY; Ng, AY (1 de enero de 2011). "Aprendizaje de características espacio-temporales invariantes jerárquicas para el reconocimiento de acciones con análisis de subespacios independientes". CVPR 2011. CVPR '11. Washington, DC, EE. UU.: IEEE Computer Society. págs. 3361–3368. CiteSeerX 10.1.1.294.5948 . doi :10.1109/CVPR.2011.5995496. ISBN .  978-1-4577-0394-2.S2CID6006618  .​
118. Grefenstette, Edward; Blunsom, Phil; de Freitas, Nando; Hermann, Karl Moritz (29 de abril de 2014). "Una arquitectura profunda para el análisis semántico". arXiv : 1404.7296 [cs.CL].
119. Mesnil, Gregoire; Deng, Li; Gao, Jianfeng; He, Xiaodong; Shen, Yelong (abril de 2014). "Aprendizaje de representaciones semánticas mediante redes neuronales convolucionales para búsquedas web – Microsoft Research". Microsoft Research . Archivado desde el original el 2017-09-15 . Consultado el 2015-12-17 .
120. Kalchbrenner, Nal; Grefenstette, Edward; Blunsom, Phil (8 de abril de 2014). "Una red neuronal convolucional para modelar oraciones". arXiv : 1404.2188 [cs.CL].
121. Kim, Yoon (25 de agosto de 2014). "Redes neuronales convolucionales para la clasificación de oraciones". arXiv : 1408.5882 [cs.CL].
122. Collobert, Ronan y Jason Weston. "Una arquitectura unificada para el procesamiento del lenguaje natural: redes neuronales profundas con aprendizaje multitarea Archivado el 4 de septiembre de 2019 en Wayback Machine ". Actas de la 25.ª conferencia internacional sobre aprendizaje automático. ACM, 2008.
123. Collobert, Ronan; Weston, Jason; Bottou, Leon; Karlen, Michael; Kavukcuoglu, Koray; Kuksa, Pavel (2 de marzo de 2011). "Procesamiento del lenguaje natural (casi) desde cero". arXiv : 1103.0398 [cs.LG].
124. Yin, W; Kann, K; Yu, M; Schütze, H (2 de marzo de 2017). "Estudio comparativo de CNN y RNN para el procesamiento del lenguaje natural". arXiv : 1702.01923 [cs.LG].
125. Bai, S.; Kolter, JS; Koltun, V. (2018). "Una evaluación empírica de redes convolucionales y recurrentes genéricas para el modelado de secuencias". arXiv : 1803.01271 [cs.LG].
126. Gruber, N. (2021). "Detección de dinámicas de acción en texto con una red neuronal recurrente". Computación neuronal y aplicaciones . 33 (12): 15709–15718. doi :10.1007/S00521-021-06190-5. S2CID  236307579.
127. Haotian, J.; Zhong, Li; Qianxiao, Li (2021). "Teoría de aproximación de arquitecturas convolucionales para modelado de series temporales". Conferencia internacional sobre aprendizaje automático . arXiv : 2107.09355 .
128. Ren, Hansheng; Xu, Bixiong; Wang, Yujing; Yi, Chao; Huang, Congrui; Kou, Xiaoyu; Xing, Tony; Yang, Mao; Tong, Jie; Zhang, Qi (2019). Servicio de detección de anomalías de series temporales en Microsoft | Actas de la 25ª Conferencia Internacional ACM SIGKDD sobre Descubrimiento de Conocimiento y Minería de Datos . arXiv : 1906.03821 . doi :10.1145/3292500.3330680. S2CID  182952311.
129. Wallach, Izhar; Dzamba, Michael; Heifets, Abraham (9 de octubre de 2015). "AtomNet: una red neuronal convolucional profunda para la predicción de la bioactividad en el descubrimiento de fármacos basado en la estructura". arXiv : 1510.02855 [cs.LG].
130. Yosinski, Jason; Clune, Jeff; Nguyen, Anh; Fuchs, Thomas; Lipson, Hod (22 de junio de 2015). "Comprensión de las redes neuronales mediante visualización profunda". arXiv : 1506.06579 [cs.CV].
131. "Una startup de Toronto tiene una forma más rápida de descubrir medicamentos efectivos". The Globe and Mail . Archivado desde el original el 20 de octubre de 2015. Consultado el 9 de noviembre de 2015 .
132. "Startup aprovecha supercomputadoras para buscar curas". KQED Future of You . 2015-05-27. Archivado desde el original el 2018-12-06 . Consultado el 2015-11-09 .
133. Chellapilla, K; Fogel, DB (1999). "Evolución de redes neuronales para jugar a las damas sin depender del conocimiento de expertos". IEEE Trans Neural Netw . 10 (6): 1382–91. doi :10.1109/72.809083. PMID  18252639.
134. Chellapilla, K.; Fogel, DB (2001). "Desarrollo de un programa para jugar a las damas a nivel experto sin utilizar la experiencia humana". IEEE Transactions on Evolutionary Computation . 5 (4): 422–428. doi :10.1109/4235.942536.
135. Fogel, David (2001). Blondie24: Jugando al límite de la IA . San Francisco, CA: Morgan Kaufmann. ISBN 978-1558607835.
136. Clark, Christopher; Storkey, Amos (2014). "Enseñanza de redes neuronales convolucionales profundas para jugar Go". arXiv : 1412.3409 [cs.AI].
137. Maddison, Chris J.; Huang, Aja; Sutskever, Ilya; Silver, David (2014). "Evaluación de movimientos en Go utilizando redes neuronales convolucionales profundas". arXiv : 1412.6564 [cs.LG].
138. «AlphaGo – Google DeepMind». Archivado desde el original el 30 de enero de 2016 . Consultado el 30 de enero de 2016 .
139. Bai, Shaojie; Kolter, J. Zico; Koltun, Vladlen (19 de abril de 2018). "Una evaluación empírica de redes convolucionales y recurrentes genéricas para el modelado de secuencias". arXiv : 1803.01271 [cs.LG].
140. Yu, Fisher; Koltun, Vladlen (30 de abril de 2016). "Agregación de contexto multiescala mediante convoluciones dilatadas". arXiv : 1511.07122 [cs.CV].
141. Borovykh, Anastasia; Bohte, Sander; Oosterlee, Cornelis W. (17 de septiembre de 2018). "Pronóstico de series temporales condicionales con redes neuronales convolucionales". arXiv : 1703.04691 [stat.ML].
142. Mittelman, Roni (3 de agosto de 2015). "Modelado de series temporales con redes neuronales totalmente convolucionales no diezmadas". arXiv : 1508.00317 [stat.ML].
143. Chen, Yitian; Kang, Yanfei; Chen, Yixiong; Wang, Zizhuo (11 de junio de 2019). "Predicción probabilística con red neuronal convolucional temporal". arXiv : 1906.04397 [estad.ML].
144. Zhao, Bendong; Lu, Huanzhang; Chen, Shangfeng; Liu, Junliang; Wu, Dongya (1 de febrero de 2017). "Redes neuronales convolucionales para series temporales de clasificación". Revista de Ingeniería de Sistemas y Electrónica . 28 (1): 162–169. doi :10.21629/JSEE.2017.01.18.
145. Petneházi, Gábor (21 de agosto de 2019). "QCNN: red neuronal convolucional cuantil". arXiv : 1908.07978 [cs.LG].
146. Hubert Mara (7 de junio de 2019), HeiCuBeDa Hilprecht: conjunto de datos de referencia cuneiformes de Heidelberg para la colección Hilprecht (en alemán), heiDATA: repositorio institucional de datos de investigación de la Universidad de Heidelberg, doi : 10.11588/data/IE8CCN
147. Hubert Mara y Bartosz Bogacz (2019), "Descifrando el código de las tablillas rotas: el desafío del aprendizaje de la escritura cuneiforme anotada en conjuntos de datos 2D y 3D normalizados", Actas de la 15.ª Conferencia internacional sobre análisis y reconocimiento de documentos (ICDAR) (en alemán), Sídney, Australia, págs. 148-153, doi :10.1109/ICDAR.2019.00032, ISBN 978-1-7281-3014-9, Número de identificación del sujeto  211026941
148. Bogacz, Bartosz; Mara, Hubert (2020), "Clasificación periódica de tablillas cuneiformes 3D con redes neuronales geométricas", Actas de la 17.ª Conferencia internacional sobre las fronteras del reconocimiento de la escritura a mano (ICFHR) , Dortmund, Alemania
149. Presentación del artículo del ICFHR sobre la clasificación de períodos de tablillas cuneiformes 3D con redes neuronales geométricas en YouTube
150. Durjoy Sen Maitra; Ujjwal Bhattacharya; SK Parui, "Enfoque común basado en CNN para el reconocimiento de caracteres manuscritos de múltiples escrituras" Archivado el 16 de octubre de 2023 en Wayback Machine , en Análisis y reconocimiento de documentos (ICDAR), 13.ª Conferencia internacional sobre 2015, vol., n.º, págs. 1021-1025, 23-26 de agosto de 2015
151. "NIPS 2017". Simposio sobre aprendizaje automático interpretable . 2017-10-20. Archivado desde el original el 2019-09-07 . Consultado el 2018-09-12 .
152. Zang, Jinliang; Wang, Le; Liu, Ziyi; Zhang, Qilin; Hua, Gang; Zheng, Nanning (2018). "Red neuronal convolucional ponderada temporal basada en la atención para el reconocimiento de acciones". Aplicaciones e innovaciones de la inteligencia artificial . IFIP Avances en tecnología de la información y la comunicación. Vol. 519. Cham: Springer International Publishing. págs. 97–108. arXiv : 1803.07179 . doi :10.1007/978-3-319-92007-8_9. ISBN 978-3-319-92006-1. ISSN  1868-4238. S2CID  4058889.
153. Wang, Le; Zang, Jinliang; Zhang, Qilin; Niu, Zhenxing; Hua, Gang; Zheng, Nanning (21 de junio de 2018). "Reconocimiento de acciones mediante una red neuronal convolucional ponderada temporal consciente de la atención" (PDF) . Sensors . 18 (7): 1979. Bibcode :2018Senso..18.1979W. doi : 10.3390/s18071979 . ISSN  1424-8220. PMC 6069475 . PMID  29933555. Archivado (PDF) desde el original el 13 de septiembre de 2018 . Consultado el 14 de septiembre de 2018 . 
154. Ong, Hao Yi; Chavez, Kevin; Hong, Augustus (18 de agosto de 2015). "Q-Learning profundo distribuido". arXiv : 1508.04186v2 [cs.LG].
155. Mnih, Volodymyr; et al. (2015). "Control a nivel humano mediante aprendizaje de refuerzo profundo". Nature . 518 (7540): 529–533. Bibcode :2015Natur.518..529M. doi :10.1038/nature14236. PMID  25719670. S2CID  205242740.
156. Sun, R.; Sessions, C. (junio de 2000). "Autosegmentación de secuencias: formación automática de jerarquías de comportamientos secuenciales". IEEE Transactions on Systems, Man, and Cybernetics - Part B: Cybernetics . 30 (3): 403–418. CiteSeerX 10.1.1.11.226 . doi :10.1109/3477.846230. ISSN  1083-4419. PMID  18252373. 
157. "Redes de creencias profundas convolucionales en CIFAR-10" (PDF) . Archivado (PDF) desde el original el 2017-08-30 . Consultado el 2017-08-18 .
158. Lee, Honglak; Grosse, Roger; Ranganath, Rajesh; Ng, Andrew Y. (1 de enero de 2009). "Redes de creencias profundas convolucionales para el aprendizaje escalable no supervisado de representaciones jerárquicas". Actas de la 26.ª Conferencia internacional anual sobre aprendizaje automático . ACM. págs. 609–616. CiteSeerX 10.1.1.149.6800 . doi :10.1145/1553374.1553453. ISBN.  9781605585161.S2CID12008458  .​
159. Behnke, Sven (2003). Redes neuronales jerárquicas para la interpretación de imágenes (PDF) . Apuntes de clase en informática. Vol. 2766. Springer. doi :10.1007/b11963. ISBN. 978-3-540-40722-5. S2CID  1304548. Archivado (PDF) del original el 10 de agosto de 2017. Consultado el 28 de diciembre de 2016 .
160. Cade Metz (18 de mayo de 2016). «Google construyó sus propios chips para impulsar sus robots de inteligencia artificial». Wired . Archivado desde el original el 13 de enero de 2018. Consultado el 6 de marzo de 2017 .

Enlaces externos

• CS231n: Redes neuronales convolucionales para reconocimiento visual: curso de informática de Stanford de Andrej Karpathy sobre CNN en visión artificial
• vdumoulin/conv_arithmetic: Informe técnico sobre aritmética de convolución en el contexto del aprendizaje profundo. Animaciones de convoluciones.