Número complejo dividido

Los reales con una raíz cuadrada extra de +1 adjunta

En álgebra , un número complejo dividido (o número hiperbólico , también número perplejo , número doble ) se basa en una unidad hiperbólica j que satisface Un número complejo dividido tiene dos componentes de números reales x e y , y se escribe El conjugado de z es Dado que el producto de un número z con su conjugado es una forma cuadrática isótropa . ${\displaystyle j^{2}=1.}$ ${\displaystyle z=x+yj.}$ ${\displaystyle z^{*}=x-yj.}$ ${\displaystyle j^{2}=1,}$ ${\displaystyle N(z):=zz^{*}=x^{2}-y^{2},}$

La colección D de todos los números complejos descompuestos para ⁠ ⁠ forma un álgebra sobre el cuerpo de números reales . Dos números complejos descompuestos w y z tienen un producto wz que satisface Esta composición de N sobre el producto del álgebra hace que ( D , +, ×, *) sea un álgebra de composición . ${\displaystyle z=x+yj}$ ${\displaystyle x,y\in \mathbb {R} }$ ${\displaystyle N(wz)=N(w)N(z).}$

Un álgebra similar basada en ⁠ ⁠ ${\displaystyle \mathbb {R} ^{2}}$ y operaciones de adición y multiplicación por componentes, ⁠ ⁠ ${\displaystyle (\mathbb {R} ^{2},+,\times ,xy),}$ donde xy es la forma cuadrática en ⁠ ⁠ ${\displaystyle \mathbb {R} ^{2},}$ también forma un espacio cuadrático . El isomorfismo de anillo

$${\displaystyle {\begin{aligned}D&\to \mathbb {R} ^{2}\\x+yj&\mapsto (x-y,x+y)\end{aligned}}}$$

relaciona formas cuadráticas proporcionales, pero la aplicación no es una isometría ya que la identidad multiplicativa (1, 1) de ⁠ ⁠ ${\displaystyle \mathbb {R} ^{2}}$ está a una distancia ⁠ ⁠ ${\displaystyle {\sqrt {2}}}$ de 0, que está normalizada en D .

Los números complejos divididos tienen muchos otros nombres; consulte el apartado Sinónimos a continuación. Consulte el artículo Variable motora para conocer las funciones de un número complejo dividido.

Definición

Un número complejo dividido es un par ordenado de números reales, escrito en la forma

$${\displaystyle z=x+jy}$$

donde x e y son números reales y la unidad hiperbólica ^[1] j satisface

$${\displaystyle j^{2}=+1}$$

En el campo de los números complejos la unidad imaginaria i satisface El cambio de signo distingue los números complejos desdoblados de los complejos ordinarios. La unidad hiperbólica j no es un número real sino una cantidad independiente. ${\displaystyle i^{2}=-1.}$

La colección de todos esos z se llama plano complejo dividido . La suma y multiplicación de números complejos divididos se definen por

$${\displaystyle {\begin{aligned}(x+jy)+(u+jv)&=(x+u)+j(y+v)\\(x+jy)(u+jv)&=(xu+yv)+j(xv+yu).\end{aligned}}}$$

Esta multiplicación es conmutativa , asociativa y se distribuye sobre la suma.

Forma conjugada, módulo y bilineal

Al igual que para los números complejos, se puede definir la noción de un complejo conjugado dividido . Si

$${\displaystyle z=x+jy~,}$$

entonces el conjugado de z se define como

$${\displaystyle z^{*}=x-jy~.}$$

El conjugado es una involución que satisface propiedades similares a las del conjugado complejo . Es decir,

$${\displaystyle {\begin{aligned}(z+w)^{*}&=z^{*}+w^{*}\\(zw)^{*}&=z^{*}w^{*}\\\left(z^{*}\right)^{*}&=z.\end{aligned}}}$$

El módulo al cuadrado de un número complejo dividido se da por la forma cuadrática isótropa ${\displaystyle z=x+jy}$

$${\displaystyle \lVert z\rVert ^{2}=zz^{*}=z^{*}z=x^{2}-y^{2}~.}$$

Tiene la propiedad del álgebra de composición :

$${\displaystyle \lVert zw\rVert =\lVert z\rVert \lVert w\rVert ~.}$$

Sin embargo, esta forma cuadrática no es definida positiva sino que tiene la signatura (1, −1) , por lo que el módulo no es una norma .

La forma bilineal asociada viene dada por

$${\displaystyle \langle z,w\rangle =\operatorname {\mathrm {Re} } \left(zw^{*}\right)=\operatorname {\mathrm {Re} } \left(z^{*}w\right)=xu-yv~,}$$

donde y Aquí, la parte real está definida por . Otra expresión para el módulo al cuadrado es entonces ${\displaystyle z=x+jy}$ ${\displaystyle w=u+jv.}$ ${\displaystyle \operatorname {\mathrm {Re} } (z)={\tfrac {1}{2}}(z+z^{*})=x}$

$${\displaystyle \lVert z\rVert ^{2}=\langle z,z\rangle ~.}$$

Como no es definida positiva, esta forma bilineal no es un producto interno ; sin embargo, a menudo se hace referencia a la forma bilineal como un producto interno indefinido . Un abuso similar del lenguaje se refiere al módulo como una norma.

Un número complejo desdoblable es invertible si y solo si su módulo es distinto de cero ( ), ${\displaystyle \lVert z\rVert \neq 0}$ por lo que los números de la forma x ± jx no tienen inverso. El inverso multiplicativo de un elemento invertible está dado por

$${\displaystyle z^{-1}={\frac {z^{*}}{{\lVert z\rVert }^{2}}}~.}$$

Los números complejos desdoblados que no son invertibles se denominan vectores nulos . Todos ellos tienen la forma ( a ± ja ) para algún número real a .

La base diagonal

Hay dos elementos idempotentes no triviales dados por y Recuerde que idempotente significa que y Ambos elementos son nulos: ${\displaystyle e={\tfrac {1}{2}}(1-j)}$ ${\displaystyle e^{*}={\tfrac {1}{2}}(1+j).}$ ${\displaystyle ee=e}$ ${\displaystyle e^{*}e^{*}=e^{*}.}$

$${\displaystyle \lVert e\rVert =\lVert e^{*}\rVert =e^{*}e=0~.}$$

A menudo resulta conveniente utilizar e y e ^{∗ como} base alternativa para el plano complejo dividido. Esta base se denomina base diagonal o base nula . El número complejo dividido z se puede escribir en la base nula como

$${\displaystyle z=x+jy=(x-y)e+(x+y)e^{*}~.}$$

Si denotamos el número para los números reales a y b por ( a , b ) , entonces la multiplicación compleja dividida está dada por ${\displaystyle z=ae+be^{*}}$

$${\displaystyle \left(a_{1},b_{1}\right)\left(a_{2},b_{2}\right)=\left(a_{1}a_{2},b_{1}b_{2}\right)~.}$$

El conjugado complejo dividido en la base diagonal está dado por y el módulo al cuadrado por $${\displaystyle (a,b)^{*}=(b,a)}$$

$${\displaystyle \lVert (a,b)\rVert ^{2}=ab.}$$

Isomorfismo

Este diagrama conmutativo relaciona la acción del versor hiperbólico sobre D con la función de compresión σ aplicada a ⁠ ⁠ ${\displaystyle \mathbb {R} ^{2}}$

Sobre la base {e, e*} resulta claro que los números complejos divididos son anillo-isomorfos a la suma directa ⁠ ⁠ ${\displaystyle \mathbb {R} \oplus \mathbb {R} }$ con adición y multiplicación definidas por pares.

La base diagonal para el plano de números complejos divididos se puede invocar utilizando un par ordenado ( x , y ) para y haciendo la asignación ${\displaystyle z=x+jy}$

$${\displaystyle (u,v)=(x,y){\begin{pmatrix}1&1\\1&-1\end{pmatrix}}=(x,y)S~.}$$

Ahora la forma cuadrática es Además, ${\displaystyle uv=(x+y)(x-y)=x^{2}-y^{2}~.}$

$${\displaystyle (\cosh a,\sinh a){\begin{pmatrix}1&1\\1&-1\end{pmatrix}}=\left(e^{a},e^{-a}\right)}$$

De esta forma las dos hipérbolas parametrizadas se ponen en correspondencia con S .

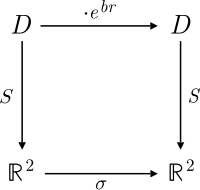
La acción del versor hiperbólico corresponde entonces, bajo esta transformación lineal, a una aplicación de compresión. ${\displaystyle e^{bj}\!}$

$${\displaystyle \sigma :(u,v)\mapsto \left(ru,{\frac {v}{r}}\right),\quad r=e^{b}~.}$$

Aunque se encuentran en la misma clase de isomorfismo en la categoría de anillos , el plano complejo dividido y la suma directa de dos líneas reales difieren en su disposición en el plano cartesiano . El isomorfismo, como aplicación planar, consiste en una rotación en sentido antihorario de 45° y una dilatación de √ 2. La dilatación en particular ha causado a veces confusión en relación con las áreas de un sector hiperbólico . De hecho, el ángulo hiperbólico corresponde al área de un sector en el plano con ${\displaystyle \mathbb {R} \oplus \mathbb {R} }$ su "círculo unitario" dado por La hipérbola unitaria contraída del plano complejo dividido tiene solo la mitad del área en el lapso de un sector hiperbólico correspondiente. Tal confusión puede perpetuarse cuando la geometría del plano complejo dividido no se distingue de la de . ${\displaystyle \{(a,b)\in \mathbb {R} \oplus \mathbb {R} :ab=1\}.}$ ${\displaystyle \{\cosh a+j\sinh a:a\in \mathbb {R} \}}$ ${\displaystyle \mathbb {R} \oplus \mathbb {R} }$

Geometría

  Hipérbola unitaria: ‖ z ‖ = 1

  Hipérbola conjugada: ‖ z ‖ = −1

  Asíntotas: ‖ z ‖ = 0

Un espacio vectorial real bidimensional con el producto interno de Minkowski se llama espacio de Minkowski (1 + 1) -dimensional , a menudo denotado como ⁠ ⁠ Así como gran parte de la geometría del plano euclidiano ⁠ ⁠ se puede describir con números complejos, la geometría del plano de Minkowski ⁠ ⁠ se puede describir con números complejos divididos. ${\displaystyle \mathbb {R} ^{1,1}.}$ ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \mathbb {R} ^{1,1}}$

El conjunto de puntos

$${\displaystyle \left\{z:\lVert z\rVert ^{2}=a^{2}\right\}}$$

es una hipérbola para cada a distinto de cero en ⁠ ⁠ ${\displaystyle \mathbb {R} .}$ La hipérbola consta de una rama derecha e izquierda que pasa por ( a , 0) y (− a , 0) . El caso a = 1 se llama hipérbola unitaria . La hipérbola conjugada está dada por

$${\displaystyle \left\{z:\lVert z\rVert ^{2}=-a^{2}\right\}}$$

con una rama superior e inferior que pasan por (0, a ) y (0, − a ) . La hipérbola y la hipérbola conjugada están separadas por dos asíntotas diagonales que forman el conjunto de elementos nulos:

$${\displaystyle \left\{z:\lVert z\rVert =0\right\}.}$$

Estas dos líneas (a veces llamadas cono nulo ) son perpendiculares en ⁠ ⁠ ${\displaystyle \mathbb {R} ^{2}}$ y tienen pendientes ±1.

Se dice que los números complejos divididos z y w son hiperbólicos-ortogonales si ⟨ z , w ⟩ = 0 . Si bien es análoga a la ortogonalidad ordinaria, particularmente como se la conoce en la aritmética de números complejos ordinaria, esta condición es más sutil. Forma la base del concepto de hiperplano simultáneo en el espacio-tiempo.

El análogo de la fórmula de Euler para los números complejos divididos es

$${\displaystyle \exp(j\theta )=\cosh(\theta )+j\sinh(\theta ).}$$

Esta fórmula se puede derivar de una expansión de serie de potencias usando el hecho de que cosh solo tiene potencias pares mientras que la de sinh tiene potencias impares. ^[2] Para todos los valores reales del ángulo hiperbólico θ, el número complejo dividido λ = exp( jθ ) tiene norma 1 y se encuentra en la rama derecha de la hipérbola unitaria. Números como λ se han llamado versores hiperbólicos .

Como λ tiene módulo 1, al multiplicar cualquier número complejo dividido z por λ se conserva el módulo de z y se representa una rotación hiperbólica (también llamada aumento de Lorentz o aplicación de compresión ). Al multiplicar por λ se conserva la estructura geométrica, tomando las hipérbolas como propias y el cono nulo como propio.

El conjunto de todas las transformaciones del plano complejo desdoblado que preservan el módulo (o equivalentemente, el producto interno) forma un grupo llamado grupo ortogonal generalizado O(1, 1) . Este grupo consta de las rotaciones hiperbólicas, que forman un subgrupo denotado SO ⁺ (1, 1) , combinado con cuatro reflexiones discretas dadas por

$${\displaystyle z\mapsto \pm z}$$y ${\displaystyle z\mapsto \pm z^{*}.}$

El mapa exponencial

$${\displaystyle \exp \colon (\mathbb {R} ,+)\to \mathrm {SO} ^{+}(1,1)}$$

enviar θ a rotación por exp( jθ ) es un isomorfismo de grupo ya que se aplica la fórmula exponencial habitual:

$${\displaystyle e^{j(\theta +\phi )}=e^{j\theta }e^{j\phi }.}$$

Si un número complejo dividido z no se encuentra en una de las diagonales, entonces z tiene una descomposición polar .

Propiedades algebraicas

En términos de álgebra abstracta , los números complejos divididos se pueden describir como el cociente del anillo polinomial por el ${\displaystyle \mathbb {R} [x]}$ ideal generado por el polinomio. ${\displaystyle x^{2}-1,}$

$${\displaystyle \mathbb {R} [x]/(x^{2}-1).}$$

La imagen de x en el cociente es la unidad "imaginaria" j . Con esta descripción, queda claro que los números complejos desdoblados forman un álgebra conmutativa sobre los números reales. El álgebra no es un cuerpo, ya que los elementos nulos no son invertibles. Todos los elementos nulos distintos de cero son divisores de cero .

Dado que la suma y la multiplicación son operaciones continuas con respecto a la topología habitual del plano, los números complejos divididos forman un anillo topológico .

El álgebra de números complejos divididos forma un álgebra de composición ya que

$${\displaystyle \lVert zw\rVert =\lVert z\rVert \lVert w\rVert ~}$$

para cualquier número z y w .

De la definición se desprende que el anillo de números complejos desdoblados es isomorfo al anillo de grupo del grupo cíclico C ₂ sobre los números reales . ${\displaystyle \mathbb {R} [C_{2}]}$ ${\displaystyle \mathbb {R} .}$

Representaciones matriciales

Los números complejos divididos se pueden representar fácilmente mediante matrices . El número complejo dividido se puede representar mediante la matriz ${\displaystyle z=x+jy}$ ${\displaystyle z\mapsto {\begin{pmatrix}x&y\\y&x\end{pmatrix}}.}$

La suma y multiplicación de números complejos descompuestos se obtiene mediante la suma y multiplicación de matrices. El módulo al cuadrado de z se obtiene mediante el determinante de la matriz correspondiente.

De hecho, existen muchas representaciones del plano complejo dividido en el anillo de cuatro dimensiones de matrices reales 2x2. Los múltiplos reales de la matriz identidad forman una línea real en el anillo de matrices M(2,R). Cualquier unidad hiperbólica m proporciona un elemento base con el que extender la línea real al plano complejo dividido. Las matrices

$${\displaystyle m={\begin{pmatrix}a&c\\b&-a\end{pmatrix}}}$$

¿Qué cuadrado de la matriz identidad satisface? Por ejemplo, cuando a = 0, entonces ( b, c ) es un punto en la hipérbola estándar. De manera más general, existe una hipersuperficie en M(2, R) de unidades hiperbólicas, cualquiera de las cuales sirve como base para representar los números complejos divididos como un subanillo de M(2, R). ^{[3] [ se necesita una mejor fuente ]} ${\displaystyle a^{2}+bc=1.}$

El número puede representarse mediante la matriz   ${\displaystyle z=x+jy}$ ${\displaystyle x\ I+y\ m.}$

Historia

El uso de números complejos divididos se remonta a 1848 cuando James Cockle reveló sus tessarinas . ^[4] William Kingdon Clifford usó números complejos divididos para representar sumas de espines. Clifford introdujo el uso de números complejos divididos como coeficientes en un álgebra de cuaterniones ahora llamada biquaternions divididos . Llamó a sus elementos "motores", un término en paralelo con la acción "rotor" de un número complejo ordinario tomado del grupo del círculo . Extendiendo la analogía, las funciones de una variable motora contrastan con las funciones de una variable compleja ordinaria .

Desde finales del siglo XX, la multiplicación de complejos divididos se ha visto comúnmente como un impulso de Lorentz de un plano espacio-temporal . ^{[5] [6] [7] [8] [9] [10]} En ese modelo, el número z = x + y j representa un evento en un plano espacio-temporal, donde x se mide en segundos e y en segundos luz . El futuro corresponde al cuadrante de eventos { z  : | y | < x } , que tiene la descomposición polar de complejos divididos . El modelo dice que se puede llegar a z desde el origen ingresando a un marco de referencia de rapidez a y esperando ρ nanosegundos. La ecuación de complejos divididos ${\displaystyle z=\rho e^{aj}\!}$

$${\displaystyle e^{aj}\ e^{bj}=e^{(a+b)j}}$$

La expresión de productos en la hipérbola unitaria ilustra la aditividad de las rapidezes para velocidades colineales. La simultaneidad de eventos depende de la rapidez a ;

$${\displaystyle \{z=\sigma je^{aj}:\sigma \in \mathbb {R} \}}$$

es la línea de acontecimientos simultáneos al origen en el marco de referencia con rapidez a .

Dos eventos z y w son hiperbólicos-ortogonales cuando los eventos canónicos exp( aj ) y j exp( aj ) son hiperbólicos ortogonales y se encuentran en los ejes de un marco de referencia en el que los eventos simultáneos al origen son proporcionales a j exp( aj ) . ${\displaystyle z^{*}w+zw^{*}=0.}$

En 1933 Max Zorn estaba usando los octoniones divididos y notó la propiedad del álgebra de composición . Se dio cuenta de que la construcción de Cayley-Dickson , usada para generar álgebras de división, podía ser modificada (con un factor gamma, γ ) para construir otras álgebras de composición incluyendo los octoniones divididos. Su innovación fue perpetuada por Adrian Albert , Richard D. Schafer y otros. ^[11] El factor gamma, con R como campo base, construye números complejos divididos como un álgebra de composición. Revisando Albert para Mathematical Reviews , NH McCoy escribió que había una "introducción de algunas nuevas álgebras de orden 2 ^e sobre F que generalizaban las álgebras de Cayley-Dickson". ^[12] Tomar F = R y e = 1 corresponde al álgebra de este artículo.

En 1935 JC Vignaux y A. Durañona y Vedia desarrollaron el álgebra geométrica compleja dividida y la teoría de funciones en cuatro artículos en Contribución a las Ciencias Físicas y Matemáticas , Universidad Nacional de La Plata , República Argentina (en español). Estos ensayos expositivos y pedagógicos presentaron el tema para una amplia apreciación. ^[13]

En 1941, EF Allen utilizó la aritmética geométrica compleja dividida para establecer la hipérbola de nueve puntos de un triángulo inscrito en  zz ^∗ = 1 . ^[14]

En 1956, Mieczyslaw Warmus publicó "Cálculo de aproximaciones" en el Bulletin de l'Académie polonaise des sciences (véase el enlace en Referencias). Desarrolló dos sistemas algebraicos, a cada uno de los cuales llamó "números aproximados", el segundo de los cuales forma un álgebra real. ^[15] DH Lehmer revisó el artículo en Mathematical Reviews y observó que este segundo sistema era isomorfo a los números "complejos hiperbólicos", el tema de este artículo.

En 1961 Warmus continuó su exposición, refiriéndose a los componentes de un número aproximado como punto medio y radio del intervalo denotado.

Sinónimos

Diferentes autores han utilizado una gran variedad de nombres para los números complejos desdoblados. Algunos de ellos son:

• ( Real ) tessarinas , James Cockle (1848)
• Motores ( algebraicos ) , W. K. Clifford (1882)
• números complejos hiperbólicos , JC Vignaux (1935), G. Cree (1949) ^[16]
• números bireales , U. Bencivenga (1946)
• números hiperbólicos reales , N. Smith (1949) ^[17]
• Números aproximados , Warmus (1956), para uso en análisis de intervalos.
• números dobles , IM Yaglom (1968), Kantor y Solodovnikov (1989), Hazewinkel (1990), Rooney (2014)
• números hiperbólicos , W. Miller y R. Boehning (1968), ^[18] G. Sobczyk (1995)
• Números anormales y complejos , W. Benz (1973)
• Números perplejos , P. Fjelstad (1986) y Poodiack & LeClair (2009)
• contracomplejo o hiperbólico , Carmody (1988)
• Números de Lorentz , F. R. Harvey (1990)
• números semicomplejos , F. Antonuccio (1994)
• números paracomplejos , Cruceanu, Fortuny y Gadea (1996)
• números complejos divididos , B. Rosenfeld (1997) ^[19]
• Números del espacio-tiempo , N. Borota (2000)
• Estudio de números , P. Lounesto (2001)
• dos números complejos , S. Olariu (2002)
• Binarios divididos , K. McCrimmon (2004)

Véase también

• Espacio Minkowski
• Cuaternión dividido
• Número hipercomplejo

Referencias

1. Vladimir V. Kisil (2012) Geometría de las transformaciones de Möbius: acciones elípticas, parabólicas e hiperbólicas de SL(2,R) , páginas 2, 161, Imperial College Press ISBN  978-1-84816-858-9
2. James Cockle (1848) Sobre un nuevo imaginario en álgebra, Philosophical Magazine 33:438
3. Álgebra abstracta/Matrices reales 2x2 en Wikilibros
4. James Cockle (1849) Sobre un nuevo imaginario en álgebra 34:37–47, London-Edinburgh-Dublin Philosophical Magazine (3) 33 :435–9, enlace desde Biodiversity Heritage Library .
5. Francesco Antonuccio (1994) Análisis semicomplejo y física matemática
6. F. Catoni, D. Boccaletti, R. Cannata, V. Catoni, E. Nichelatti, P. Zampetti. (2008) Las matemáticas del espacio-tiempo de Minkowski , Birkhäuser Verlag , Basilea. Capítulo 4: Trigonometría en el plano de Minkowski. ISBN 978-3-7643-8613-9 . 
7. Francesco Catoni; Dino Boccaletti; Roberto Cannata; Vincenzo Catoni; Paolo Zampetti (2011). "Capítulo 2: Números hiperbólicos". Geometría del Espacio-Tiempo de Minkowski . Medios de ciencia y negocios de Springer. ISBN 978-3-642-17977-8.
8. Fjelstad, Paul (1986), "Extensión de la relatividad especial a través de los números perplejos", American Journal of Physics , 54 (5): 416–422, Bibcode :1986AmJPh..54..416F, doi :10.1119/1.14605
9. Louis Kauffman (1985) "Transformaciones en relatividad especial", Revista Internacional de Física Teórica 24:223–36.
10. Sobczyk, G.(1995) Hyperbolic Number Plane, también publicado en College Mathematics Journal 26:268–80.
11. Robert B. Brown (1967) Sobre álgebras generalizadas de Cayley-Dickson, Pacific Journal of Mathematics 20(3):415–22, enlace desde Project Euclid .
12. NH McCoy (1942) Revisión de "Formas cuadráticas que permiten la composición" por AA Albert, Mathematical Reviews #0006140
13. Vignaux, J.(1935) "Sobre el numero complejo hiperbolico y su relacion con la geometria de Borel", Contribución al Estudio de las Ciencias Físicas y Matemáticas , Universidad Nacional de la Plata, República Argentina
14. Allen, EF (1941) "Sobre un triángulo inscrito en una hipérbola rectangular", American Mathematical Monthly 48(10): 675–681
15. M. Warmus (1956) "Cálculo de aproximaciones" Archivado el 9 de marzo de 2012 en Wayback Machine , Bulletin de l'Académie polonaise des sciences , vol. 4, n.º 5, págs. 253-257, MR 0081372
16. Cree, George C. (1949). La teoría de números de un sistema de números complejos hiperbólicos (tesis de maestría). Universidad McGill.
17. Smith, Norman E. (1949). Introducción a la teoría de números hiperbólicos (tesis de maestría). Universidad McGill.
18. Miller, William; Boehning, Rochelle (1968). "Números gaussianos, parabólicos e hiperbólicos". El profesor de matemáticas . 61 (4): 377–382. doi :10.5951/MT.61.4.0377. JSTOR  27957849.
19. Rosenfeld, B. (1997) Geometría de grupos de Lie , página 30, Kluwer Academic Publishers ISBN 0-7923-4390-5 

Lectura adicional

• Bencivenga, Uldrico (1946) "Sulla rappresentazione geometrica delle algebre doppie dotate di modulo", Atti della Reale Accademia delle Scienze e Belle-Lettere di Napoli , Ser (3) v.2 No7. SEÑOR 0021123.
• Walter Benz (1973) Vorlesungen úber Geometrie der Algebren , Springer
• NA Borota, E. Flores y TJ Osler (2000) "Números espacio-temporales de forma sencilla", Mathematics and Computer Education 34: 159–168.
• NA Borota y TJ Osler (2002) "Funciones de una variable espacio-temporal", Mathematics and Computer Education 36: 231–239.
• K. Carmody, (1988) "Cuaterniones, octoniones y sedeniones circulares e hiperbólicos", Appl. Math. Comput. 28:47–72.
• K. Carmody, (1997) "Cuaterniones, octoniones y sedeniones circulares e hiperbólicos: resultados adicionales", Appl. Math. Comput. 84:27–48.
• William Kingdon Clifford (1882) Mathematical Works , editor de AW Tucker, página 392, "Notas adicionales sobre bicuaterniones"
• V. Cruceanu, P. Fortuny y PM Gadea (1996) Una encuesta sobre geometría paracompleja, Rocky Mountain Journal of Mathematics 26(1): 83–115, enlace desde Project Euclid .
• De Boer, R. (1987) "También conocida como lista de números perplejos", American Journal of Physics 55(4):296.
• Anthony A. Harkin y Joseph B. Harkin (2004) Geometría de números complejos generalizados, Mathematics Magazine 77(2):118–29.
• F. Reese Harvey. Spinors and calibrations. Academic Press, San Diego. 1990. ISBN 0-12-329650-1 . Contiene una descripción de álgebras normalizadas en signatura indefinida, incluidos los números de Lorentz. 
• Hazewinkle, M. (1994) "Números dobles y duales", Enciclopedia de Matemáticas , Soviet/AMS/Kluwer, Dordrect.
• Kevin McCrimmon (2004) Una muestra de las álgebras de Jordan , págs. 66, 157, Universitext, Springer ISBN 0-387-95447-3 MR 2014924 
• C. Musès, "Hipernúmeros aplicados: conceptos computacionales", Appl. Math. Comput. 3 (1977) 211–226.
• C. Musès, "Hipernúmeros II: conceptos adicionales y aplicaciones computacionales", Appl. Math. Comput. 4 (1978) 45–66.
• Olariu, Silviu (2002) Números complejos en N dimensiones , Capítulo 1: Números complejos hiperbólicos en dos dimensiones, páginas 1–16, North-Holland Mathematics Studies #190, Elsevier ISBN 0-444-51123-7 . 
• Poodiack, Robert D. y Kevin J. LeClair (2009) "Teoremas fundamentales del álgebra para los perplejos", The College Mathematics Journal 40(5):322–35.
• Isaak Yaglom (1968) Números complejos en geometría , traducido por E. Primrose del original ruso de 1963, Academic Press , págs. 18-20.
• J. Rooney (2014). "Números complejos generalizados en mecánica". En Marco Ceccarelli y Victor A. Glazunov (ed.). Avances en la teoría y la práctica de robots y manipuladores: Actas de Romansy 2014 XX Simposio CISM-IFToMM sobre teoría y práctica de robots y manipuladores . Mecanismos y ciencia de las máquinas. Vol. 22. Springer. págs. 55–62. doi :10.1007/978-3-319-07058-2_7. ISBN 978-3-319-07058-2.