Coherencia (física)

La coherencia expresa la posibilidad de que dos ondas interfieran . Dos haces monocromáticos de una misma fuente siempre interfieren. ^[1]^{: 286} Las fuentes de ondas no son estrictamente monocromáticas: pueden ser parcialmente coherentes . Los haces de diferentes fuentes son mutuamente incoherentes .

Cuando se produce una interferencia, dos ondas se suman para crear una onda de mayor amplitud que cualquiera de ellas ( interferencia constructiva ) o se restan entre sí para crear una onda de mínimos que pueden ser cero ^[1]^{: 286} (interferencia destructiva), dependiendo de su fase relativa . La interferencia constructiva o destructiva son casos límite, y dos ondas siempre interfieren, incluso si el resultado de la suma es complicado o no destacable.

Dos ondas con una fase relativa constante serán coherentes. ^[2] La cantidad de coherencia se puede medir fácilmente mediante la visibilidad de interferencia , que analiza el tamaño de las franjas de interferencia en relación con las ondas de entrada (a medida que varía el desfase de fase); una definición matemática precisa del grado de coherencia se da mediante funciones de correlación. En términos más generales, la coherencia describe la similitud estadística de un campo (campo electromagnético, paquete de ondas cuánticas, etc.) en dos puntos del espacio o del tiempo. ^[3]

Concepto cualitativo

Dos rendijas iluminadas por una fuente muestran un patrón de interferencia. La fuente está situada a la izquierda del diagrama, detrás de los colimadores que crean un haz paralelo. Esta combinación garantiza que una onda procedente de la fuente incida en ambas rendijas en la misma parte del ciclo de onda: la onda tendrá *coherencia* .

La coherencia controla la visibilidad o el contraste de los patrones de interferencia. Por ejemplo, la visibilidad del patrón del experimento de doble rendija requiere que ambas rendijas estén iluminadas por una onda coherente, como se ilustra en la figura. Las fuentes grandes sin colimación o las fuentes que mezclan muchas frecuencias diferentes tendrán una visibilidad menor. ^[4]^{: 264}

La coherencia contiene varios conceptos distintos. La coherencia espacial describe la correlación (o relación predecible) entre ondas en diferentes puntos del espacio, ya sea lateral o longitudinal. ^[5] La coherencia temporal describe la correlación entre ondas observadas en diferentes momentos del tiempo. Ambos se observan en el experimento de Michelson-Morley y en el experimento de interferencia de Young . Una vez que se obtienen las franjas en el interferómetro de Michelson , cuando uno de los espejos se aleja gradualmente del divisor de haz, el tiempo que tarda el haz en viajar aumenta y las franjas se vuelven opacas y finalmente desaparecen, mostrando coherencia temporal. De manera similar, en un experimento de doble rendija , si se aumenta el espacio entre las dos rendijas, la coherencia muere gradualmente y finalmente las franjas desaparecen, mostrando coherencia espacial. En ambos casos, la amplitud de la franja desaparece lentamente, a medida que la diferencia de trayectoria aumenta más allá de la longitud de coherencia.

La coherencia se concibió originalmente en relación con el experimento de doble rendija de Thomas Young en óptica , pero ahora se utiliza en cualquier campo que involucre ondas, como la acústica , la ingeniería eléctrica , la neurociencia y la mecánica cuántica . La propiedad de la coherencia es la base de aplicaciones comerciales como la holografía , el giroscopio Sagnac , los conjuntos de antenas de radio , la tomografía de coherencia óptica y los interferómetros de telescopios ( interferómetros ópticos astronómicos y radiotelescopios ).

Definición matemática

La función de coherencia entre dos señales se define como ^[6] ${\estilo de visualización x(t)}$ $y(t)$

\gamma _{xy}^{2}(f)={\frac {|S_{xy}(f)|^{2}}{S_{xx}(f)S_{yy}(f)}}

donde es la densidad espectral cruzada de la señal y y son las funciones de densidad espectral de potencia de y , respectivamente. La densidad espectral cruzada y la densidad espectral de potencia se definen como las transformadas de Fourier de las señales de correlación cruzada y autocorrelación , respectivamente. Por ejemplo, si las señales son funciones del tiempo, la correlación cruzada es una medida de la similitud de las dos señales en función del desfase temporal entre sí y la autocorrelación es una medida de la similitud de cada señal consigo misma en diferentes instantes de tiempo. En este caso, la coherencia es una función de la frecuencia. Análogamente, si y son funciones del espacio, la correlación cruzada mide la similitud de dos señales en diferentes puntos del espacio y las autocorrelaciones la similitud de la señal con respecto a sí misma para una cierta distancia de separación. En ese caso, la coherencia es una función del número de onda (frecuencia espacial). $Estilo de visualización S_ {xy}(f)}$ $Estilo de visualización S_{xx}(f)$ $Estilo de visualización S_{yy}(f)$ ${\estilo de visualización x(t)}$ $y(t)$ ${\estilo de visualización x(t)}$ $y(t)$

La coherencia varía en el intervalo . Si esto significa que las señales están perfectamente correlacionadas o relacionadas linealmente y si están totalmente descorrelacionadas. Si se mide un sistema lineal, siendo la entrada y la salida, la función de coherencia será unitaria en todo el espectro. Sin embargo, si existen no linealidades en el sistema, la coherencia variará en el límite dado anteriormente. $0\leq \gamma _{xy}^{2}(f)\leq 1$ $Estilo de visualización: gamma _{xy}^{2}(f)=1$ $Estilo de visualización: gamma _{xy}^{2}(f)=0$ ${\estilo de visualización x(t)}$ $y(t)$

Coherencia y correlación

La coherencia de dos ondas expresa cuán bien correlacionadas están las ondas, cuantificada por la función de correlación cruzada . ^[7]^[1]^[8]^[9]^[10] La correlación cruzada cuantifica la capacidad de predecir la fase de la segunda onda conociendo la fase de la primera. Como ejemplo, considere dos ondas perfectamente correlacionadas para todo momento (usando una fuente de luz monocromática). En cualquier momento, la diferencia de fase entre las dos ondas será constante. Si, cuando se combinan, exhiben una interferencia constructiva perfecta, una interferencia destructiva perfecta o algo intermedio pero con una diferencia de fase constante, entonces se deduce que son perfectamente coherentes. Como se discutirá más adelante, la segunda onda no necesita ser una entidad separada. Podría ser la primera onda en un momento o posición diferente. En este caso, la medida de correlación es la función de autocorrelación (a veces llamada autocoherencia ). El grado de correlación involucra funciones de correlación. ^[11]^{: 545-550}

Ejemplos de estados ondulatorios

Estos estados están unificados por el hecho de que su comportamiento está descrito por una ecuación de onda o alguna generalización de la misma.

Ondas en una cuerda (arriba y abajo) o slinky (compresión y expansión)
Ondas superficiales en un líquido
Señales electromagnéticas (campos) en líneas de transmisión
Sonido
Ondas de radio y microondas
Ondas de luz ( óptica )
Ondas de materia asociadas, por ejemplo, con electrones y átomos.

En sistemas con ondas macroscópicas, se puede medir la onda directamente. En consecuencia, se puede calcular fácilmente su correlación con otra onda. Sin embargo, en óptica no se puede medir el campo eléctrico directamente, ya que oscila mucho más rápido que la resolución temporal de cualquier detector. ^[12] En cambio, se mide la intensidad de la luz. La mayoría de los conceptos relacionados con la coherencia que se presentarán a continuación se desarrollaron en el campo de la óptica y luego se utilizaron en otros campos. Por lo tanto, muchas de las mediciones estándar de coherencia son mediciones indirectas, incluso en campos en los que la onda se puede medir directamente.

Coherencia temporal

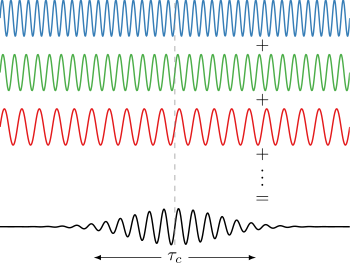
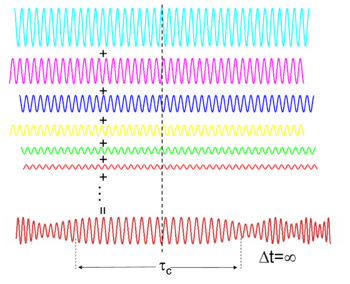
La coherencia temporal es la medida de la correlación media entre el valor de una onda y el de ella misma con un retraso de , en cualquier par de tiempos. La coherencia temporal nos indica lo monocromática que es una fuente. En otras palabras, caracteriza lo bien que una onda puede interferir consigo misma en un tiempo diferente. El retraso en el que la fase o amplitud se desvía en una cantidad significativa (y por lo tanto la correlación disminuye en una cantidad significativa) se define como el tiempo de coherencia . Con un retraso de el grado de coherencia es perfecto, mientras que cae significativamente a medida que el retraso pasa . La longitud de coherencia se define como la distancia que recorre la onda en el tiempo . ^[11]^{: 560, 571–573} ${\estilo de visualización \tau}$ $\tau _{\mathrm {c} }$ $\tau = 0$ $\tau =\tau _{\mathrm {c} }$ $L_{\mathrm {c} }$ $\tau _{\mathrm {c} }$

El tiempo de coherencia no es la duración temporal de la señal; la longitud de coherencia difiere del área de coherencia (ver más abajo).

Relación entre el tiempo de coherencia y el ancho de banda

Cuanto mayor sea el ancho de banda (rango de frecuencias Δf que contiene una onda), más rápido se decorrelaciona la onda (y, por lo tanto, más pequeña es): ^[11]^{: 358–359, 560} $\tau _{\mathrm {c} }$

\tau _{c}\Delta f\gtrsim 1.

Formalmente, esto se desprende del teorema de convolución en matemáticas, que relaciona la transformada de Fourier del espectro de potencia (la intensidad de cada frecuencia) con su autocorrelación. ^[11]^{: 572}

Los láseres de ancho de banda estrecho tienen longitudes de coherencia largas (hasta cientos de metros). Por ejemplo, un láser de helio-neón estabilizado y monomodo puede producir fácilmente luz con longitudes de coherencia de 300 m. ^{[15] Sin embargo, no todos los láseres tienen una alta monocromaticidad (por ejemplo, para un}láser de zafiro de titanio con modo bloqueado , Δλ ≈ 2 nm – 70 nm).

Los LED se caracterizan por Δλ ≈ 50 nm, y las luces de filamento de tungsteno exhiben Δλ ≈ 600 nm, por lo que estas fuentes tienen tiempos de coherencia más cortos que la mayoría de los láseres monocromáticos.

Ejemplos de coherencia temporal

Algunos ejemplos de coherencia temporal son:

Una onda que contiene una sola frecuencia (monocromática) está perfectamente correlacionada consigo misma en todos los retardos de tiempo, de acuerdo con la relación anterior. (Ver Figura 1)
Por el contrario, una onda cuya fase se desvía rápidamente tendrá un tiempo de coherencia corto. (Ver Figura 2)
De manera similar, los pulsos ( paquetes de ondas ) de ondas, que naturalmente tienen un amplio rango de frecuencias, también tienen un tiempo de coherencia corto, ya que la amplitud de la onda cambia rápidamente. (Véase la Figura 3)
Por último, la luz blanca, que tiene un rango de frecuencias muy amplio, es una onda que varía rápidamente tanto en amplitud como en fase. Como tiene, por lo tanto, un tiempo de coherencia muy corto (apenas 10 períodos aproximadamente), a menudo se la llama incoherente.

La holografía requiere luz con un tiempo de coherencia largo. En cambio, la tomografía de coherencia óptica , en su versión clásica, utiliza luz con un tiempo de coherencia corto.

Medición de la coherencia temporal

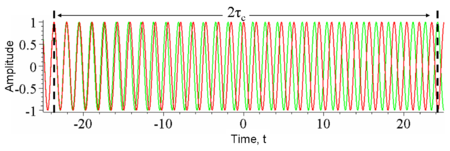
En óptica, la coherencia temporal se mide en un interferómetro como el interferómetro de Michelson o el interferómetro de Mach–Zehnder . En estos dispositivos, una onda se combina con una copia de sí misma que se retrasa un tiempo . Un detector mide la intensidad promediada en el tiempo de la luz que sale del interferómetro. La visibilidad resultante del patrón de interferencia (p. ej., consulte la Figura 4) proporciona la coherencia temporal en el retraso . Dado que para la mayoría de las fuentes de luz natural, el tiempo de coherencia es mucho más corto que la resolución temporal de cualquier detector, el propio detector realiza el promedio temporal. Considere el ejemplo que se muestra en la Figura 3. En un retraso fijo, aquí , un detector infinitamente rápido mediría una intensidad que fluctúa significativamente durante un tiempo t igual a . En este caso, para encontrar la coherencia temporal en , se promediaría manualmente la intensidad en el tiempo. ${\estilo de visualización \tau}$ ${\estilo de visualización \tau}$ ${\estilo de visualización 2\tau}$ ${\estilo de visualización \tau}$ ${\ Displaystyle 2 \ tau _ {\ mathrm {c}}}$

Coherencia espacial

En algunos sistemas, como las ondas de agua o la óptica, los estados ondulatorios pueden extenderse sobre una o dos dimensiones. La coherencia espacial describe la capacidad de dos puntos espaciales x ₁ y x ₂ en la extensión de una onda para interferir cuando se promedian en el tiempo. Más precisamente, la coherencia espacial es la correlación cruzada entre dos puntos en una onda para todos los tiempos. Si una onda tiene solo 1 valor de amplitud en una longitud infinita, es perfectamente coherente espacialmente. El rango de separación entre los dos puntos sobre los que hay una interferencia significativa define el diámetro del área de coherencia, ^[16] (La longitud de coherencia , a menudo una característica de una fuente, suele ser un término industrial relacionado con el tiempo de coherencia de la fuente, no el área de coherencia en el medio). es el tipo de coherencia relevante para el interferómetro de doble rendija de Young. También se utiliza en sistemas de imágenes ópticas y, en particular, en varios tipos de telescopios astronómicos. $A_{\mathrm {c} }$ $l_{\mathrm {c} }$ $A_{\mathrm {c} }$

A una distancia de una fuente incoherente con área de superficie , ${\estilo de visualización z}$ $A_{\mathrm {s} }$ $A_{\mathrm {c} }={\frac {\lambda ^{2}z^{2}}{A_{\mathrm {s} }}}$

A veces la gente también utiliza "coherencia espacial" para referirse a la visibilidad cuando un estado ondulatorio se combina con una copia de sí mismo desplazada espacialmente.

Ejemplos

Coherencia espacial
Figura 5: Una onda plana con una longitud de coherencia infinita .
Figura 6: Una onda con un perfil variable (frente de onda) y una longitud de coherencia infinita.
Figura 7: Una onda con un perfil variable (frente de onda) y una longitud de coherencia finita.
$Figura 8: Una onda con un área de coherencia finita incide sobre un orificio (pequeña abertura). La onda se difractará fuera del orificio. Lejos del orificio, los frentes de onda esféricos emergentes son aproximadamente planos. El área de coherencia ahora es infinita mientras que la longitud de coherencia permanece invariable.$
Figura 8: Una onda con un área de coherencia finita incide sobre un orificio (pequeña abertura). La onda se difractará fuera del orificio. Lejos del orificio, los frentes de onda esféricos emergentes son aproximadamente planos. El área de coherencia ahora es infinita mientras que la longitud de coherencia permanece invariable.
Figura 9: Una onda con un área de coherencia infinita se combina con una copia de sí misma desplazada espacialmente. Algunas secciones de la onda interfieren de manera constructiva y otras de manera destructiva. Al promediar estas secciones, un detector con una longitud D medirá una visibilidad de interferencia reducida. Por ejemplo, un interferómetro de Mach-Zehnder desalineado hará esto.

Consideremos el filamento de una bombilla de tungsteno. Los distintos puntos del filamento emiten luz de forma independiente y no tienen una relación de fase fija. En detalle, en cualquier momento el perfil de la luz emitida se distorsionará. El perfil cambiará aleatoriamente a lo largo del tiempo de coherencia . Dado que una fuente de luz blanca, como una bombilla , es pequeña, el filamento se considera una fuente espacialmente incoherente. Por el contrario, un conjunto de antenas de radio tiene una gran coherencia espacial porque las antenas en los extremos opuestos del conjunto emiten con una relación de fase fija. Las ondas de luz producidas por un láser suelen tener una coherencia temporal y espacial elevada (aunque el grado de coherencia depende en gran medida de las propiedades exactas del láser). La coherencia espacial de los rayos láser también se manifiesta como patrones de motas y franjas de difracción que se ven en los bordes de la sombra. $\tau_{c}$ $\tau_{c}$

La holografía requiere luz coherente en el tiempo y en el espacio. Su inventor, Dennis Gabor , produjo hologramas exitosos más de diez años antes de que se inventaran los láseres. Para producir luz coherente, hizo pasar la luz monocromática de una línea de emisión de una lámpara de vapor de mercurio a través de un filtro espacial estenopeico.

En febrero de 2011 se informó que los átomos de helio , enfriados hasta casi el cero absoluto / estado de condensado de Bose-Einstein , pueden fluir y comportarse como un haz coherente como ocurre en un láser. ^[17]^[18] Además, se encontró que las propiedades de coherencia de la luz de salida de las estructuras ópticas no lineales multimodo obedecen a la teoría termodinámica óptica. ^[19]

Coherencia espectral de pulsos cortos

Las ondas de diferentes frecuencias (en la luz, son de diferentes colores) pueden interferir para formar un pulso si tienen una relación de fase relativa fija (ver transformada de Fourier ). Por el contrario, si las ondas de diferentes frecuencias no son coherentes, entonces, al combinarse, crean una onda que es continua en el tiempo (por ejemplo, luz blanca o ruido blanco ). La duración temporal del pulso está limitada por el ancho de banda espectral de la luz según: $\Delta t$ $\Delta f$

\Delta f\Delta t\geq 1

lo que se desprende de las propiedades de la transformada de Fourier y da como resultado el principio de incertidumbre de Küpfmüller (para las partículas cuánticas también da como resultado el principio de incertidumbre de Heisenberg ).

Si la fase depende linealmente de la frecuencia (es decir, ), entonces el pulso tendrá la duración mínima para su ancho de banda (un pulso limitado por la transformada ); de lo contrario, se produce un chirrido (ver dispersión ). $\theta (f)\propto f$

Medición de la coherencia espectral

La medición de la coherencia espectral de la luz requiere un interferómetro óptico no lineal , como un correlador óptico de intensidad , un interferómetro óptico con resolución de frecuencia (FROG) o una interferometría de fase espectral para la reconstrucción directa del campo eléctrico (SPIDER).

Polarización y coherencia

La luz también tiene una polarización , que es la dirección en la que oscila el campo eléctrico o magnético. La luz no polarizada está compuesta de ondas de luz incoherentes con ángulos de polarización aleatorios. El campo eléctrico de la luz no polarizada se desplaza en todas las direcciones y cambia de fase a lo largo del tiempo de coherencia de las dos ondas de luz. Un polarizador absorbente girado en cualquier ángulo siempre transmitirá la mitad de la intensidad incidente cuando se promedie a lo largo del tiempo.

Si el campo eléctrico se desvía en una cantidad menor, la luz se polarizará parcialmente, de modo que en un ángulo determinado, el polarizador transmitirá más de la mitad de la intensidad. Si una onda se combina con una copia de sí misma polarizada ortogonalmente con un retraso menor que el tiempo de coherencia, se crea una luz parcialmente polarizada.

La polarización de un haz de luz se representa mediante un vector en la esfera de Poincaré . En el caso de la luz polarizada, el extremo del vector se encuentra en la superficie de la esfera, mientras que en el caso de la luz no polarizada, el vector tiene una longitud cero. El vector de la luz parcialmente polarizada se encuentra dentro de la esfera.

Coherencia cuántica

La propiedad característica de las ondas de materia cuántica , la interferencia de ondas, se basa en la coherencia. Si bien inicialmente se basaba en la coherencia óptica, la teoría y la comprensión experimental de la coherencia cuántica ampliaron enormemente el tema. ^[20]

Coherencia de ondas de materia

La extensión más simple de la coherencia óptica aplica conceptos ópticos a las ondas de materia . Por ejemplo, al realizar el experimento de doble rendija con átomos en lugar de ondas de luz, un haz atómico suficientemente colimado crea una función de onda atómica coherente que ilumina ambas rendijas. ^[21] Cada rendija actúa como un haz separado pero en fase que contribuye al patrón de intensidad en una pantalla. Estas dos contribuciones dan lugar a un patrón de intensidad de bandas brillantes debido a la interferencia constructiva, entrelazadas con bandas oscuras debido a la interferencia destructiva, en una pantalla posterior. Se han demostrado muchas variaciones de este experimento. ^[22]^{: 1057}

Al igual que con la luz, la coherencia transversal (a través de la dirección de propagación) de las ondas de materia está controlada por la colimación. Debido a que la luz, en todas las frecuencias, viaja a la misma velocidad, la coherencia longitudinal y temporal están vinculadas; en las ondas de materia, estas son independientes. En las ondas de materia, la selección de la velocidad (energía) controla la coherencia longitudinal y la pulsación o el corte controla la coherencia temporal. ^[21]^{: 154}

Óptica cuántica

El descubrimiento del efecto Hanbury Brown y Twiss (correlación de la luz en función de la coincidencia) impulsó la creación por parte de Glauber ^[23] de un análisis de coherencia cuántica único. La coherencia óptica clásica se convierte en un límite clásico para la coherencia cuántica de primer orden; un mayor grado de coherencia conduce a muchos fenómenos en la óptica cuántica .

Coherencia cuántica macroscópica

La coherencia cuántica a escala macroscópica conduce a fenómenos novedosos, los llamados fenómenos cuánticos macroscópicos . Por ejemplo, el láser , la superconductividad y la superfluidez son ejemplos de sistemas cuánticos altamente coherentes cuyos efectos son evidentes a escala macroscópica. La coherencia cuántica macroscópica (orden de largo alcance fuera de la diagonal, ODLRO) ^[24]^[25] para la superfluidez y la luz láser, está relacionada con la coherencia de primer orden (1 cuerpo)/ODLRO, mientras que la superconductividad está relacionada con la coherencia de segundo orden/ODLRO. (Para los fermiones, como los electrones, solo son posibles órdenes pares de coherencia/ODLRO). Para los bosones, un condensado de Bose-Einstein es un ejemplo de un sistema que exhibe coherencia cuántica macroscópica a través de un estado de partícula única ocupada múltiple.

El campo electromagnético clásico muestra coherencia cuántica macroscópica. El ejemplo más obvio es la señal portadora de radio y televisión. Ambas cumplen la descripción cuántica de coherencia de Glauber .

La coherencia cuántica como recurso

Recientemente, MB Plenio y sus colaboradores construyeron una formulación operacional de la coherencia cuántica como una teoría de recursos. Introdujeron monótonos de coherencia análogos a los monótonos de entrelazamiento. ^[26] Se ha demostrado que la coherencia cuántica es equivalente al entrelazamiento cuántico ^[27] en el sentido de que la coherencia puede describirse fielmente como entrelazamiento y, a la inversa, que cada medida de entrelazamiento corresponde a una medida de coherencia.

Aplicaciones

Holografía

Las superposiciones coherentes de campos de ondas ópticas incluyen la holografía. Las fotografías holográficas se han utilizado como arte y como etiquetas de seguridad difíciles de falsificar.

Campos de ondas no ópticas

Otras aplicaciones se refieren a la superposición coherente de campos de ondas no ópticas . En mecánica cuántica, por ejemplo, se considera un campo de probabilidad, que está relacionado con la función de onda (interpretación: densidad de la amplitud de probabilidad). Las aplicaciones se refieren, entre otras, a las futuras tecnologías de computación cuántica y a la tecnología ya disponible de criptografía cuántica . Además, se tratan los problemas del siguiente subcapítulo. $\psi (\mathbf {r} )$

Análisis modal

La coherencia se utiliza para comprobar la calidad de las funciones de transferencia (FRF) que se miden. Una coherencia baja puede deberse a una mala relación señal/ruido o a una resolución de frecuencia inadecuada.

Véase también

Coherencia atómica – Tipo de estado de un sistema átomo-campo electromagnético
Longitud de coherencia : distancia a lo largo de la cual una onda que se propaga mantiene un cierto grado de coherencia.
Estados coherentes – Estado cuántico específico de un oscilador armónico cuántico
Ancho de línea láser : el ancho de línea espectral de un rayo láser
Medición en mecánica cuántica : interacción de un sistema cuántico con un observador clásico
Problema de medición – Problema teórico en física cuántica
Radiación monocromática : radiación electromagnética con una única frecuencia constante.
Función de coherencia mutua
Detección heterodina óptica
Biología cuántica : aplicación de la mecánica cuántica y la química teórica a objetos y problemas biológicos
Efecto Quantum Zeno – Fenómeno de medición cuántica
Superposición de ondas : Principio fundamental de la física que establece que las soluciones físicas de los sistemas lineales son lineales.

Referencias

^ abc M. Born; E. Wolf (1999). Principios de óptica (7.ª ed.). Cambridge University Press . ISBN 978-0-521-64222-4.
^ Rudiger, Paschotta. «Artículo sobre coherencia en la RP Photonics Encyclopedia». RP Photonics Encyclopedia . Consultado el 7 de junio de 2023 .
^ Wolf, Emil (2007). Introducción a la teoría de la coherencia y la polarización de la luz . Cambridge: Cambridge University Press. ISBN 978-0-521-82211-4.OCLC 149011826 .
^ Born, Max; Wolf, Emil (1993). Principios de óptica: teoría electromagnética de la propagación, interferencia y difracción de la luz (6.ª ed., reimpresa (con correcciones) ed.). Oxford: Pergamon Press. ISBN 978-0-08-026481-3.
^ Hecht (1998). Óptica (3.ª ed.). Addison Wesley Longman. págs. 554–574. ISBN 978-0-201-83887-9.
^ Shin. K, Hammond. J. Fundamentos del procesamiento de señales para ingenieros de sonido y vibración . John Wiley & Sons, 2008.
^ Rolf G. Winter; Aephraim M. Steinberg (2008). "Coherencia". AccessScience . McGraw-Hill . doi :10.1036/1097-8542.146900.
^ Loudon, Rodney (2000). La teoría cuántica de la luz . Oxford University Press . ISBN 978-0-19-850177-0.
^ Leonard Mandel; Emil Wolf (1995). Coherencia óptica y óptica cuántica . Cambridge University Press . ISBN 978-0-521-41711-2.
^ Arvind Marathay (1982). Elementos de la teoría de la coherencia óptica . John Wiley & Sons . ISBN 978-0-471-56789-9.
^ abcd Hecht, Eugene (2002). Óptica (4.ª ed.). Estados Unidos de América: Addison Wesley. ISBN 978-0-8053-8566-3.
^ Peng, J.-L.; Liu, T.-A.; Shu, R.-H. (2008). "Contador de frecuencia óptica basado en dos peines láser de fibra con modo bloqueado". Applied Physics B . 92 (4): 513. Bibcode :2008ApPhB..92..513P. doi :10.1007/s00340-008-3111-6. S2CID 121675431.
^ Christopher Gerry; Peter Knight (2005). Introducción a la óptica cuántica . Cambridge University Press. ISBN 978-0-521-52735-4.
^ Esta figura debe modificarse porque, en ella, la onda verde en realidad no es una copia de la onda roja; ambas son ondas monocromáticas con frecuencias ligeramente diferentes. Una figura adecuada sería una combinación de una onda chirriante y su copia retrasada para que coincida con la figura y la descripción de la figura actual.
^ Saleh, Teich. Fundamentos de fotónica . Wiley.
^ Goodman (1985). Óptica estadística (1.ª ed.). Wiley-Interscience. pp. 210, 221. ISBN 978-0-471-01502-4.
^ Hodgman, SS; Dall, RG; Manning, AG; Baldwin, KGH; Truscott, AG (2011). "Medición directa de la coherencia de tercer orden de largo alcance en condensados de Bose-Einstein". Science . 331 (6020): 1046–1049. Bibcode :2011Sci...331.1046H. doi :10.1126/science.1198481. PMID 21350171. S2CID 5336898.
^ Pincock, S. (25 de febrero de 2011). "Un láser frío hace que los átomos marchen al compás". ABC Science . ABC News Online . Consultado el 2 de marzo de 2011 .
^ Selim, Mahmoud A.; Wu, Fan O.; Pyrialakos, Georgios G.; Khajavikhan, Mercedeh; Christodoulides, Demetrios (1 de marzo de 2023). "Propiedades de coherencia de la luz en fibras parabólicas no lineales altamente multimodales en condiciones de equilibrio óptico". Optics Letters . 48 (5): 1208–1211. arXiv : 2212.10063 . doi :10.1364/OL.483282. ISSN 1539-4794. PMID 36857250. S2CID 254877557.
^ Streltsov, Alexander; Adesso, Gerardo; Plenio, Martin B. (30 de octubre de 2017). "Coloquio: La coherencia cuántica como recurso". Reseñas de Física Moderna . 89 (4): 041003. arXiv : 1609.02439 . doi :10.1103/RevModPhys.89.041003. ISSN 0034-6861. S2CID 62899253.
^ ab Adams, CS; Sigel, M; Mlynek, J (mayo de 1994). "Óptica atómica". Physics Reports . 240 (3): 143–210. doi : 10.1016/0370-1573(94)90066-3 .
^ Cronin, Alexander D.; Schmiedmayer, Jörg; Pritchard, David E. (28 de julio de 2009). "Óptica e interferometría con átomos y moléculas". Reseñas de Física Moderna . 81 (3): 1051–1129. doi :10.1103/RevModPhys.81.1051. hdl : 1721.1/52372 . ISSN 0034-6861. S2CID 28009912.
^ Glauber, Roy J. (15 de junio de 1963). "La teoría cuántica de la coherencia óptica". Physical Review . 130 (6): 2529–2539. doi : 10.1103/PhysRev.130.2529 . ISSN 0031-899X.
^ Penrose, O.; Onsager, L. (1956). "Condensación de Bose-Einstein y helio líquido". Phys. Rev. 104 ( 3): 576–584. Código Bibliográfico :1956PhRv..104..576P. doi :10.1103/physrev.104.576.
^ Yang, CN (1962). "Concepto de orden de largo alcance fuera de la diagonal y fases cuánticas del helio líquido y de los superconductores". Rev. Mod. Phys . 34 (4): 694–704. Bibcode :1962RvMP...34..694Y. doi :10.1103/revmodphys.34.694.
^ Baumgratz, T.; Cramer, M.; Plenio, MB (2014). "Cuantificación de la coherencia". Phys. Rev. Lett . 113 (14): 140401. arXiv : 1311.0275 . Código Bibliográfico :2014PhRvL.113n0401B. doi :10.1103/physrevlett.113.140401. PMID 25325620. S2CID 45904642.
^ Tan, KC; Jeong, H. (2018). "Enredo como la porción simétrica de la coherencia correlacionada". Phys. Rev. Lett . 121 (22): 220401. arXiv : 1805.10750 . Código Bibliográfico :2018PhRvL.121v0401T. doi :10.1103/PhysRevLett.121.220401. PMID 30547638. S2CID 51690149.

Enlaces externos

Dr. SkySkull (3 de septiembre de 2008). "Conceptos básicos de óptica: coherencia". Cráneos en las estrellas .