Método de carga de imágenes

Técnica de cálculo para electrostática clásica

El método de cargas imagen (también conocido como método de imágenes y método de cargas espejo ) es una herramienta básica para la resolución de problemas en electrostática . El nombre se origina a partir de la sustitución de ciertos elementos en el diseño original por cargas ficticias, lo que replica las condiciones de contorno del problema (ver condiciones de contorno de Dirichlet o condiciones de contorno de Neumann ).

La validez del método de cargas de imagen se basa en un corolario del teorema de unicidad , que establece que el potencial eléctrico en un volumen V está determinado de forma única si se especifican tanto la densidad de carga en toda la región como el valor del potencial eléctrico en todos los límites. Alternativamente, la aplicación de este corolario a la forma diferencial de la Ley de Gauss muestra que en un volumen V rodeado de conductores y que contiene una densidad de carga especificada ρ , el campo eléctrico está determinado de forma única si se da la carga total en cada conductor. Si poseemos conocimiento del potencial eléctrico o del campo eléctrico y las condiciones de contorno correspondientes, podemos cambiar la distribución de carga que estamos considerando por una con una configuración que sea más fácil de analizar, siempre que satisfaga la ecuación de Poisson en la región de interés y asuma los valores correctos en los límites. ^[1]

Reflexión en un plano conductor

El campo de una carga positiva sobre una superficie conductora plana, encontrado mediante el método de imágenes.

Método de imágenes para un momento dipolar eléctrico en un plano conductor

Cargos puntuales

El ejemplo más simple del método de cargas de imagen es el de una carga puntual, con carga q , ubicada en encima de una placa conductora infinitamente conectada a tierra (es decir: ) en el plano xy . Para simplificar este problema, podemos reemplazar la placa de equipotencial con una carga − q , ubicada en . Esta disposición producirá el mismo campo eléctrico en cualquier punto para el cual (es decir, encima de la placa conductora), y satisface la condición de contorno de que el potencial a lo largo de la placa debe ser cero. Esta situación es equivalente a la configuración original, y por lo tanto la fuerza sobre la carga real ahora se puede calcular con la ley de Coulomb entre dos cargas puntuales. ^[2] ${\displaystyle (0,0,a)}$ ${\displaystyle V=0}$ ${\displaystyle (0,0,-a)}$ ${\displaystyle z>0}$

El potencial en cualquier punto del espacio, debido a estas dos cargas puntuales de carga + q en + a y − q en − a en el eje z , se da en coordenadas cilíndricas como

${\displaystyle V\left(\rho ,\varphi ,z\right)={\frac {1}{4\pi \varepsilon _{0}}}\left({\frac {q}{\sqrt {\rho ^{2}+\left(z-a\right)^{2}}}}+{\frac {-q}{\sqrt {\rho ^{2}+\left(z+a\right)^{2}}}}\right)\,}$

Por lo tanto, la densidad de carga superficial en el plano conectado a tierra viene dada por

${\displaystyle \sigma =-\varepsilon _{0}\left.{\frac {\partial V}{\partial z}}\right|_{z=0}={\frac {-qa}{2\pi \left(\rho ^{2}+a^{2}\right)^{3/2}}}}$

Además, la carga total inducida en el plano conductor será la integral de la densidad de carga en todo el plano, por lo que:

${\displaystyle {\begin{aligned}Q_{t}&=\int _{0}^{2\pi }\int _{0}^{\infty }\sigma \left(\rho \right)\,\rho \,d\rho \,d\theta \\[6pt]&={\frac {-qa}{2\pi }}\int _{0}^{2\pi }d\theta \int _{0}^{\infty }{\frac {\rho \,d\rho }{\left(\rho ^{2}+a^{2}\right)^{3/2}}}\\[6pt]&=-q\end{aligned}}}$

La carga total inducida en el plano resulta ser simplemente − q . Esto también se puede ver a partir de la ley de Gauss , considerando que el campo dipolar disminuye al cubo de la distancia a grandes distancias y, por lo tanto, el flujo total del campo a través de una esfera infinitamente grande se desvanece.

Debido a que los campos eléctricos satisfacen el principio de superposición , un plano conductor debajo de múltiples cargas puntuales puede ser reemplazado por las imágenes especulares de cada una de las cargas individualmente, sin necesidad de otras modificaciones.

Momentos dipolares eléctricos

La imagen de un momento dipolar eléctrico p en sobre un plano conductor infinito conectado a tierra en el plano xy es un momento dipolar en con magnitud y dirección iguales rotado azimutalmente por π. Es decir, un momento dipolar con componentes cartesianas tendrá en la imagen un momento dipolar . El dipolo experimenta una fuerza en la dirección z , dada por ${\displaystyle (0,0,a)}$ ${\displaystyle (0,0,-a)}$ ${\displaystyle (p\sin \theta \cos \phi ,p\sin \theta \sin \phi ,p\cos \theta )}$ ${\displaystyle (-p\sin \theta \cos \phi ,-p\sin \theta \sin \phi ,p\cos \theta )}$

${\displaystyle F=-{\frac {1}{4\pi \varepsilon _{0}}}{\frac {3p^{2}}{16a^{4}}}\left(1+\cos ^{2}\theta \right)}$

y un par en el plano perpendicular al dipolo y al plano conductor,

${\displaystyle \tau =-{\frac {1}{4\pi \varepsilon _{0}}}{\frac {p^{2}}{16a^{3}}}\sin 2\theta }$

Reflexión en una interfaz dieléctrica plana

De manera similar al plano conductor, se puede considerar el caso de una interfaz plana entre dos medios dieléctricos diferentes. Si se coloca una carga puntual en el dieléctrico que tiene la constante dieléctrica , entonces la interfaz (con el dieléctrico que tiene la constante dieléctrica ) desarrollará una carga de polarización ligada. Se puede demostrar que el campo eléctrico resultante dentro del dieléctrico que contiene la partícula se modifica de una manera que puede describirse por una carga imagen dentro del otro dieléctrico. Sin embargo, dentro del otro dieléctrico, la carga imagen no está presente. ^[3] ${\displaystyle q}$ ${\displaystyle \epsilon _{1}}$ ${\displaystyle \epsilon _{2}}$

A diferencia del caso del metal, la carga de la imagen no es exactamente opuesta a la carga real: . Incluso puede que no tenga el mismo signo, si la carga se coloca dentro del material dieléctrico más fuerte (las cargas se repelen de las regiones de constante dieléctrica más baja). Esto se puede ver en la fórmula. ${\displaystyle q'}$ ${\textstyle q'={\frac {\varepsilon _{1}-\varepsilon _{2}}{\varepsilon _{1}+\varepsilon _{2}}}q}$

Reflexión en una esfera conductora

Diagrama que ilustra el método de la imagen para la ecuación de Laplace para una esfera de radio R . El punto verde es una carga q que se encuentra dentro de la esfera a una distancia p del origen, el punto rojo es la imagen de ese punto, que tiene una carga − qR / p , que se encuentra fuera de la esfera a una distancia de R ² / p del origen. El potencial producido por las dos cargas es cero en la superficie de la esfera.

Líneas de campo fuera de una esfera conectada a tierra para una carga colocada fuera de la esfera.

Varias superficies requieren una serie infinita de cargas de imagen puntual.

Cargos puntuales

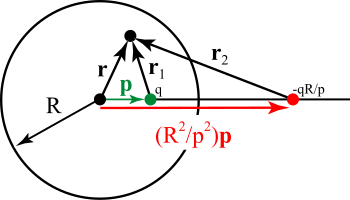
El método de imágenes también se puede aplicar a una esfera. ^[4] De hecho, el caso de cargas de imagen en un plano es un caso especial del caso de imágenes para una esfera. Refiriéndonos a la figura, deseamos encontrar el potencial dentro de una esfera conectada a tierra de radio R , centrada en el origen, debido a una carga puntual dentro de la esfera en la posición (Para el caso opuesto, el potencial fuera de una esfera debido a una carga fuera de la esfera, el método se aplica de manera similar). En la figura, esto está representado por el punto verde. Sea q la carga puntual de este punto. La imagen de esta carga con respecto a la esfera conectada a tierra se muestra en rojo. Tiene una carga de q ′ = − qR / p y se encuentra en una línea que conecta el centro de la esfera y la carga interna en el vector posición . Se puede ver que el potencial en un punto especificado por el vector de radio debido solo a ambas cargas está dado por la suma de los potenciales: ${\displaystyle \mathbf {p} }$ ${\displaystyle \left(R^{2}/p^{2}\right)\mathbf {p} }$ ${\displaystyle \mathbf {r} }$

${\displaystyle 4\pi \varepsilon _{0}V(\mathbf {r} )={\frac {q}{|\mathbf {r} _{1}|}}+{\frac {(-qR/p)}{|\mathbf {r} _{2}|}}={\frac {q}{\sqrt {r^{2}+p^{2}-2\mathbf {r} \cdot \mathbf {p} }}}+{\frac {(-qR/p)}{\sqrt {r^{2}+{\frac {R^{4}}{p^{2}}}-{\frac {2R^{2}}{p^{2}}}\mathbf {r} \cdot \mathbf {p} }}}}$

Multiplicando por la expresión más a la derecha obtenemos:

${\displaystyle V(\mathbf {r} )={\frac {1}{4\pi \varepsilon _{0}}}\left[{\frac {q}{\sqrt {r^{2}+p^{2}-2\mathbf {r} \cdot \mathbf {p} }}}-{\frac {q}{\sqrt {{\frac {r^{2}p^{2}}{R^{2}}}+R^{2}-2\mathbf {r} \cdot \mathbf {p} }}}\right]}$

y se puede ver que en la superficie de la esfera (es decir, cuando r = R ), el potencial se desvanece. El potencial dentro de la esfera está dado por la expresión anterior para el potencial de las dos cargas. Este potencial no será válido fuera de la esfera, ya que la carga imagen no existe realmente, sino que está "reemplazando" las densidades de carga superficial inducidas en la esfera por la carga interna en . El potencial fuera de la esfera conectada a tierra estará determinado solo por la distribución de carga fuera de la esfera y será independiente de la distribución de carga dentro de la esfera. Si asumimos por simplicidad (sin pérdida de generalidad) que la carga interna se encuentra en el eje z, entonces la densidad de carga inducida será simplemente una función del ángulo polar θ y está dada por: ${\displaystyle \mathbf {p} }$

${\displaystyle \sigma (\theta )=\varepsilon _{0}\left.{\frac {\partial V}{\partial r}}\right|_{r=R}={\frac {-q\left(R^{2}-p^{2}\right)}{4\pi R\left(R^{2}+p^{2}-2pR\cos \theta \right)^{3/2}}}}$

La carga total en la esfera se puede encontrar integrando todos los ángulos:

${\displaystyle Q_{t}=\int _{0}^{\pi }d\theta \int _{0}^{2\pi }d\phi \,\,\sigma (\theta )R^{2}\sin \theta =-q}$

Nótese que el problema recíproco también se resuelve con este método. Si tenemos una carga q en la posición del vector fuera de una esfera conectada a tierra de radio R , el potencial fuera de la esfera está dado por la suma de los potenciales de la carga y su carga imagen dentro de la esfera. Al igual que en el primer caso, la carga imagen tendrá carga − qR / p y estará ubicada en la posición del vector . El potencial dentro de la esfera dependerá solo de la distribución de carga real dentro de la esfera. A diferencia del primer caso, la integral tendrá el valor − qR / p . ${\displaystyle \mathbf {p} }$ ${\displaystyle \left(R^{2}/p^{2}\right)\mathbf {p} }$

Momentos dipolares eléctricos

La imagen de un dipolo puntual eléctrico es un poco más complicada. Si el dipolo se representa como dos cargas grandes separadas por una pequeña distancia, entonces la imagen del dipolo no solo tendrá las cargas modificadas por el procedimiento anterior, sino que también se modificará la distancia entre ellas. Siguiendo el procedimiento anterior, se descubre que un dipolo con un momento dipolar en la posición del vector que se encuentra dentro de la esfera de radio R tendrá una imagen ubicada en la posición del vector (es decir, la misma que para la carga simple) y tendrá una carga simple de: ${\displaystyle M}$ ${\displaystyle \mathbf {p} }$ ${\displaystyle \left(R^{2}/p^{2}\right)\mathbf {p} }$

${\displaystyle q'={\frac {R\mathbf {p} \cdot \mathbf {M} }{p^{3}}}}$

y un momento dipolar de:

${\displaystyle \mathbf {M} '=\left({\frac {R}{p}}\right)^{3}\left[-\mathbf {M} +{\frac {2\mathbf {p} (\mathbf {p} \cdot \mathbf {M} )}{p^{2}}}\right]}$

Método de inversión

El método de imágenes para una esfera conduce directamente al método de inversión. ^[5] Si tenemos una función armónica de posición donde son las coordenadas esféricas de la posición, entonces la imagen de esta función armónica en una esfera de radio R alrededor del origen será ${\displaystyle \Phi (r,\theta ,\phi )}$ ${\displaystyle r,\theta ,\phi }$

${\displaystyle \Phi '(r,\theta ,\phi )={\frac {R}{r}}\,\Phi {\left({\frac {R^{2}}{r}},\theta ,\phi \right)}}$

Si el potencial surge de un conjunto de cargas de magnitud en las posiciones , entonces el potencial imagen será el resultado de una serie de cargas de magnitud en las posiciones . De ello se deduce que si el potencial surge de una densidad de carga , entonces el potencial imagen será el resultado de una densidad de carga . ${\displaystyle \Phi }$ ${\displaystyle q_{i}}$ ${\displaystyle (r_{i},\theta _{i},\phi _{i})}$ ${\displaystyle Rq_{i}/r_{i}}$ ${\displaystyle (R^{2}/r_{i},\theta _{i},\phi _{i})}$ ${\displaystyle \Phi }$ ${\displaystyle \rho (r,\theta ,\phi )}$ ${\displaystyle \rho '(r,\theta ,\phi )=(R/r)\rho (R^{2}/r,\theta ,\phi )}$

Véase también

• Transformada de Kelvin
• Ley de Coulomb
• Teorema de divergencia
• Flujo
• Superficie gaussiana
• Principio de reflexión de Schwarz
• Teorema de unicidad de la ecuación de Poisson
• Antena de imagen
• Principio de equivalencia de superficies

Referencias

Notas

1. Griffiths, David J. (2013). Introducción a la electrodinámica (4.ª ed.) . Pearson . pág. 121. ISBN. 978-0-321-85656-2.
2. Jeans 1908, pág. 186
3. Jackson 1962, pág. 111
4. Tikhonov, Andrey N.; Samarskii, Alexander A. (1963). Ecuaciones de física matemática. Nueva York: Dover Publications . pág. 354. ISBN. 0-486-66422-8.
5. Jackson 1962, pág. 35

Fuentes

• Jackson, John D. (1962). Electrodinámica clásica. John Wiley & Sons .
• Jeans, James H. (1908). La teoría matemática de la electricidad y el magnetismo. Cambridge University Press .

Lectura adicional

• Feynman, Richard ; Leighton, Robert B .; Sands, Matthew (1989). Feynman Lectures on Physics, Mainly Electromagnetism and Matter [Conferencias Feynman sobre física , principalmente electromagnetismo y materia ], Addison-Wesley . ISBN 0-201-51003-0.
• Landau, Lev D .; Lifshitz, Evgeny M.; Pitaevskii , Lev P. (1960). Electrodinámica de medios continuos 2.ª edición . Londres: Elsevier . ISBN. 978-0-7506-2634-7.
• Purcell, Edward M. Berkeley Curso de Física, Vol. 2: Electricidad y magnetismo (2.ª ed.) . McGraw-Hill .