Bruja de Agnesi

Curva plana cúbica

Curvas de Agnesi seleccionadas (verde) y los círculos a partir de los cuales se construyen (azul), con parámetros de radio , , , y . ${\displaystyle a=1}$ ${\displaystyle a=2}$ ${\displaystyle a=4}$ ${\displaystyle a=8}$

En matemáticas , la bruja de Agnesi ( pronunciación italiana: [aɲˈɲeːzi, -eːsi; -ɛːzi] ) es una curva plana cúbica definida a partir de dos puntos diametralmente opuestos de un círculo.

La curva fue estudiada ya en 1653 por Pierre de Fermat , en 1703 por Guido Grandi y por Isaac Newton . Recibe su nombre de la matemática italiana Maria Gaetana Agnesi , quien la publicó en 1748. El nombre italiano la versiera di Agnesi se basa en el latín versoria ( lámina de veleros) y el seno versus . Esto fue leído por John Colson como l'avversiera di Agnesi , donde avversiera se traduce como "mujer que está en contra de Dios" e interpretado como "bruja". ^{[1] [2] [3] [4]}

La gráfica de la derivada de la función arcotangente constituye un ejemplo de la bruja de Agnesi. Como función de densidad de probabilidad de la distribución de Cauchy , la bruja de Agnesi tiene aplicaciones en la teoría de la probabilidad . También da lugar al fenómeno de Runge en la aproximación de funciones por polinomios , se ha utilizado para aproximar la distribución de energía de líneas espectrales y modela la forma de las colinas.

La bruja es tangente a su círculo definitorio en uno de los dos puntos de definición, y asintótica a la línea tangente al círculo en el otro punto. Tiene un vértice único (un punto de curvatura extrema) en el punto de tangencia con su círculo definitorio, que también es su círculo osculador en ese punto. También tiene dos puntos de inflexión finitos y un punto de inflexión infinito. El área entre la bruja y su línea asintótica es cuatro veces el área del círculo definitorio, y el volumen de revolución de la curva alrededor de su línea definitoria es el doble del volumen del toro de revolución de su círculo definitorio.

Construcción

La bruja de Agnesi (curva MP ) con puntos marcados

Una animación que muestra la construcción de la bruja de Agnesi.

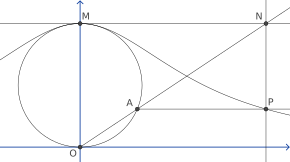
Para construir esta curva, comience con dos puntos cualesquiera O y M , y dibuje un círculo con OM como diámetro. Para cualquier otro punto A en el círculo, sea N el punto de intersección de la línea secante OA y la línea tangente en M . Sea P el punto de intersección de una línea perpendicular a OM a través de A , y una línea paralela a OM a través de N . Entonces P se encuentra en la bruja de Agnesi. La bruja consiste en todos los puntos P que se pueden construir de esta manera a partir de la misma elección de O y M . ^[5] Incluye, como caso límite, el propio punto M .

Ecuaciones

Supóngase que el punto O está en el origen y el punto M se encuentra en el eje positivo y que el círculo con diámetro OM tiene radio . Entonces la ecuación construida a partir de O y M tiene la ecuación cartesiana ^{[6] [7]} Esta ecuación se puede simplificar, eligiendo , a la forma o equivalentemente, despejando los denominadores , como la ecuación algebraica cúbica En su forma simplificada, esta curva es la gráfica de la derivada de la función arcotangente . ^[8] ${\displaystyle y}$ ${\displaystyle a}$ $${\displaystyle y={\frac {8a^{3}}{x^{2}+4a^{2}}}.}$$ ${\displaystyle a={\tfrac {1}{2}}}$ $${\displaystyle y={\frac {1}{x^{2}+1}}.}$$ $${\displaystyle (x^{2}+1)y=1.}$$

La bruja de Agnesi también puede describirse mediante ecuaciones paramétricas cuyo parámetro θ es el ángulo entre OM y OA , medido en el sentido de las agujas del reloj: ^{[6] [7]} $${\displaystyle {\begin{aligned}x&=2a\tan \theta ,\\y&=2a\cos ^{2}\theta .\end{aligned}}}$$

Propiedades

Las principales propiedades de esta curva se pueden derivar del cálculo integral . El área entre la bruja y su línea asintótica es cuatro veces el área del círculo fijo, . ^{[6] [7] [9]} El volumen de revolución de la bruja de Agnesi alrededor de su asíntota es . ^[6] Esto es dos veces el volumen del toro formado al girar el círculo que define a la bruja alrededor de la misma línea. ^[9] ${\displaystyle 4\pi a^{2}}$ ${\displaystyle 4\pi ^{2}a^{3}}$

La curva tiene un único vértice en el punto de tangencia con su círculo definitorio. Es decir, este punto es el único punto donde la curvatura alcanza un mínimo local o un máximo local. ^[10] El círculo definitorio de la bruja es también su círculo osculador en el vértice, ^[11] el único círculo que "besa" la curva en ese punto al compartir la misma orientación y curvatura. ^[12] Debido a que este es un círculo osculador en el vértice de la curva, tiene contacto de tercer orden con la curva. ^[13]

La curva tiene dos puntos de inflexión , en los puntos correspondientes a los ángulos . ^{[6] [7]} Cuando se considera como una curva en el plano proyectivo también hay un tercer punto de inflexión infinito, en el punto donde la línea en el infinito es cruzada por la línea asintótica. Debido a que uno de sus puntos de inflexión es infinito, la bruja tiene el mínimo número posible de puntos de inflexión reales finitos de cualquier curva cúbica no singular . ^[14] $${\displaystyle \left(\pm {\frac {2a}{\sqrt {3}}},{\frac {3a}{2}}\right)}$$ ${\displaystyle \theta =\pm \pi /6}$

El área más grande de un rectángulo que puede inscribirse entre la bruja y su asíntota es , ${\displaystyle 4a^{2}}$ para un rectángulo cuya altura es el radio del círculo que lo define y cuyo ancho es el doble del diámetro del círculo. ^[9]

Historia

Estudios tempranos

Ilustración de la curva y su construcción realizada por Agnesi en 1748 ^[15]

La curva fue estudiada por Pierre de Fermat en su tratado de 1659 sobre la cuadratura . En él, Fermat calcula el área bajo la curva y (sin detalles) afirma que el mismo método se aplica también a la cisoide de Diocles . Fermat escribe que la curva le fue sugerida " ab erudito geometra " [por un geómetra erudito]. ^[16] Paradís, Pla y Viader (2008) especulan que el geómetra que sugirió esta curva a Fermat podría haber sido Antoine de Laloubère . ^[17]

La construcción dada arriba para esta curva fue encontrada por Grandi (1718); la misma construcción también fue encontrada antes por Isaac Newton , pero sólo publicada póstumamente más tarde, en 1779. ^[18] Grandi (1718) también sugirió el nombre versiera (en italiano) o versoria (en latín) para la curva. ^[19] El término latino también se usa para una escota , la cuerda que hace girar la vela, pero Grandi puede haber tenido la intención de referirse simplemente a la función versine que apareció en su construcción. ^{[9] [18] [20] [21]}

En 1748, Maria Gaetana Agnesi publicó Instituzioni analitiche ad uso della gioventù italiana , un libro de texto temprano sobre cálculo . ^[15] En él, después de considerar primero otras dos curvas, incluye un estudio de esta curva. Define la curva geométricamente como el lugar geométrico de los puntos que satisfacen una cierta proporción, determina su ecuación algebraica y encuentra su vértice, línea asintótica y puntos de inflexión. ^[22]

Etimología

Maria Gaetana Agnesi nombró la curva según Grandi, versiera . ^{[20] [22]} Casualmente, en esa época en Italia era común hablar del Diablo a través de otras palabras como aversiero o versiero , derivadas del latín adversarius , el "adversario" de Dios. Versiera , en particular, se usaba para indicar a la esposa del diablo, o "bruja". ^[23] Debido a esto, el profesor de Cambridge John Colson tradujo erróneamente el nombre de la curva como "bruja". ^[24] Diferentes trabajos modernos sobre Agnesi y sobre la curva sugieren conjeturas ligeramente diferentes sobre cómo exactamente ocurrió esta traducción errónea. ^{[25] [26]} Struik menciona que: ^[22]

La palabra [ versiera ] se deriva del latín vertere , girar, pero también es una abreviatura del italiano avversiera , diabla. Algún ingenioso en Inglaterra la tradujo una vez como 'bruja', y el tonto juego de palabras todavía se conserva con cariño en la mayoría de nuestros libros de texto en idioma inglés. ... La curva ya había aparecido en los escritos de Fermat ( Oeuvres , I, 279-280; III, 233-234) y de otros; el nombre versiera proviene de Guido Grandi ( Quadratura circuli et hyperbolae , Pisa, 1703). La curva es del tipo 63 en la clasificación de Newton . ... El primero en usar el término 'bruja' en este sentido puede haber sido B. Williamson, Integral calculus , 7 (1875), 173; ^[27] véase Oxford English Dictionary .

Por otra parte, Stephen Stigler sugiere que el propio Grandi "puede haber estado recurriendo a un juego de palabras", un doble juego de palabras que conecta al diablo con la versine y la función sine con la forma del pecho femenino (ambas pueden escribirse como "seno" en italiano). ^[18]

Aplicaciones

Una versión escalada de la curva es la función de densidad de probabilidad de la distribución de Cauchy . Esta es la distribución de probabilidad en la variable aleatoria determinada por el siguiente experimento aleatorio : para un punto fijo sobre el eje , elija uniformemente al azar una línea que pase por , y sea la coordenada del punto donde esta línea aleatoria cruza el eje. La distribución de Cauchy tiene una distribución puntiaguda que se asemeja visualmente a la distribución normal , pero sus colas pesadas le impiden tener un valor esperado según las definiciones habituales, a pesar de su simetría. En términos de la propia bruja, esto significa que la coordenada del centroide de la región entre la curva y su línea asintótica no está bien definida, a pesar de la simetría y el área finita de esta región. ^{[18] [28]} ${\displaystyle x}$ ${\displaystyle p}$ ${\displaystyle x}$ ${\displaystyle p}$ ${\displaystyle x}$ ${\displaystyle x}$

En el análisis numérico , cuando se aproximan funciones mediante interpolación polinómica con puntos de interpolación igualmente espaciados, puede darse el caso de que para algunas funciones el uso de más puntos cree peores aproximaciones, de modo que la interpolación diverja de la función que está tratando de aproximar en lugar de converger hacia ella. Este comportamiento paradójico se denomina fenómeno de Runge . Fue descubierto por primera vez por Carl David Tolmé Runge para la función de Runge , otra versión escalada de la bruja de Agnesi, al interpolar esta función sobre el intervalo . El mismo fenómeno ocurre para la propia bruja sobre el intervalo más amplio . ^[29] ${\displaystyle y=1/(1+25x^{2})}$ ${\displaystyle [-1,1]}$ ${\displaystyle y=1/(1+x^{2})}$ ${\displaystyle [-5,5]}$

La bruja de Agnesi aproxima la distribución de energía espectral de las líneas espectrales , particularmente las líneas de rayos X. ^[30]

La sección transversal de una colina lisa tiene una forma similar a la de la bruja. ^[31] Las curvas con esta forma se han utilizado como obstáculo topográfico genérico en un flujo en el modelado matemático. ^{[32] [33]} Las olas solitarias en aguas profundas también pueden adoptar esta forma. ^{[34] [35]}

Gottfried Wilhelm Leibniz utilizó una versión de esta curva para derivar la fórmula de Leibniz para π . Esta fórmula, la serie infinita, se puede derivar igualando el área bajo la curva con la integral de la función , utilizando la expansión de la serie de Taylor de esta función como la serie geométrica infinita e integrando término por término. ^[7] $${\displaystyle {\frac {\pi }{4}}=1\,-\,{\frac {1}{3}}\,+\,{\frac {1}{5}}\,-\,{\frac {1}{7}}\,+\,{\frac {1}{9}}\,-\,\cdots ,}$$ ${\displaystyle 1/(1+x^{2})}$ ${\displaystyle 1-x^{2}+x^{4}-x^{6}+\cdots }$

En la cultura popular

La bruja de Agnesi es el título de una novela de Robert Spiller. Incluye una escena en la que un profesor da una versión de la historia del término. ^[36]

Witch of Agnesi es también el título de un álbum musical del cuarteto de jazz Radius. La portada del álbum presenta una imagen de la construcción de la bruja. ^[37]

Referencias

1. Wolfram MathWorld, La bruja de Agnesi
2. Lynn M. Osen: Mujeres en las matemáticas. MIT Press, Cambridge MA 1975, ISBN 0-262-15014-X, pág. 45.
3. Simon Singh : El enigma de Fermat. La búsqueda para resolver el mayor problema matemático del mundo. Walker Books, Nueva York 1997, ISBN 0-471-27047-4, pág. 100.
4. David J. Darling: El libro universal de las matemáticas. Desde Abracadabra hasta las paradojas de Zenón. Wiley International, Hoboken NJ 2004, ISBN 0-8027-1331-9, pág. 8.
5. Eagles, Thomas Henry (1885), "La bruja de Agnesi", Geometría constructiva de curvas planas: con numerosos ejemplos , Macmillan and Company, págs. 313-314
6. Lawrence, J. Dennis (2013), "4.3 La bruja de Agnesi (Fermat, 1666; Agnesi, 1748)", Un catálogo de curvas planas especiales , Dover Books on Mathematics, Courier Corporation, págs. 90-93, ISBN 9780486167664
7. Yates, Robert C. (1954), "La bruja de Agnesi", Curvas y sus propiedades (PDF) , Classics in Mathematics Education, vol. 4, Consejo Nacional de Profesores de Matemáticas, págs. 237-238
8. Cohen, David W.; Henle, James M. (2005), Cálculo: el lenguaje del cambio, Jones & Bartlett Learning, pág. 351, ISBN 9780763729479
9. Larsen, Harold D. (enero de 1946), "La bruja de Agnesi", School Science and Mathematics , 46 (1): 57–62, doi :10.1111/j.1949-8594.1946.tb04418.x
10. Gibson, CG (2001), Geometría elemental de curvas diferenciables: una introducción para estudiantes de grado , Cambridge: Cambridge University Press, Ejercicio 9.1.9, pág. 131, doi :10.1017/CBO9781139173377, ISBN 0-521-80453-1, Sr.  1855907
11. Haftendorn, Dörte (2017), "4.1 Versiera, die Hexenkurve", Kurven erkunden und verstehen (en alemán), Springer, págs. 79–91, doi :10.1007/978-3-658-14749-5, ISBN 978-3-658-14748-8. Para el círculo osculador, véase en particular la pág. 81: "Der erzeugende Kreis ist der Krümmungskreis der weiten Versiera in ihrem Scheitel".
12. Lipsman, Ronald L.; Rosenberg, Jonathan M. (2017), Cálculo multivariable con MATLAB®: con aplicaciones a la geometría y la física, Springer, pág. 42, ISBN 9783319650708El círculo "besa" la curva con precisión de segundo orden, por lo que recibe el nombre de círculo osculador (de la palabra latina que significa "besar").
13. Fuchs, Dmitry ; Tabachnikov, Serge (2007), Ómnibus matemático: treinta conferencias sobre matemáticas clásicas, Providence, RI: American Mathematical Society, pág. 142, doi :10.1090/mbk/046, ISBN 978-0-8218-4316-1, Sr.  2350979
14. Arnold, VI (2005), "El principio de economía topológica en geometría algebraica", Encuestas en matemáticas modernas , London Mathematical Society Lecture Note Series, vol. 321, Cambridge: Cambridge University Press, págs. 13-23, doi :10.1017/CBO9780511614156.003, ISBN 978-0-521-54793-2, Sr.  2166922. Véanse en particular las páginas 15 y 16.
15. Agnesi, Maria Gaetana (1748), Instituzioni analitiche ad uso della gioventú italianaVéase en particular el problema 3, págs. 380-382, y la figura 135.
16. de Fermat, Pierre (1891), Oevres (en latín), vol. 1, Gauthier-Villars et fils, págs. 280-285
17. Paradís, Jaume; Pla, Josep; Viader, Pelegrí (2008), "Método de cuadratura de Fermat", Revue d'Histoire des Mathématiques , 14 (1): 5–51, MR  2493381, archivado desde el original el 8 de agosto de 2019 , recuperado 18 de mayo 2018
18. Stigler, Stephen M. (agosto de 1974), "Estudios en la historia de la probabilidad y la estadística. XXXIII. Cauchy y la bruja de Agnesi: una nota histórica sobre la distribución de Cauchy", Biometrika , 61 (2): 375–380, doi :10.1093/biomet/61.2.375, JSTOR  2334368, MR  0370838
19. En sus notas al "Trattato del moto naturalmente accelerato" de Galileo, Grandi se había referido a "quella curva che io descrivo nel mio libro delle quadrature [1703], alla prop. IV, nata da' seni versi, che da me suole chiamarsi Versiera , en latino però Versoria ." Véase Galilei, Opere , 3: 393. Se encuentra el nuevo término en Lorenzo Lorenzini, Exercitatio geométrica , xxxi: "sit pro exemplo curva illa, quam Doctissimus magnusque geometra Guido Grandus versoria nominat".
20. Truesdell, C. (1991), "Corrección y adiciones para "Maria Gaetana Agnesi"", Archivo de Historia de las Ciencias Exactas , 43 (4): 385–386, doi : 10.1007/BF00374764 , […] nata da' seni versi, che da me suole chiamarsi la Versiera in latino però Versoria […]
21. Grandi, G. (1718), "Note al trattato del Galileo del moto naturale accellerato", Opera Di Galileo Galilei (en italiano), vol. III, Florencia, pág. 393Como lo cita Stigler (1974).
22. Se puede encontrar una traducción del trabajo de Agnesi sobre esta curva en: Struik, Dirk J. (1969), A Source Book in Mathematics, 1200–1800, Cambridge, Massachusetts: Harvard University Press, pp. 178–180
23. Pietro Fanfani , Vocabolario dell'uso toscano , p. 334
24. Mulcrone, TF (1957), "Los nombres de la curva de Agnesi", American Mathematical Monthly , 64 (5): 359–361, doi :10.2307/2309605, JSTOR  2309605, MR  0085163
25. Singh, Simon (1997), El enigma de Fermat: La búsqueda épica para resolver el mayor problema matemático del mundo , Nueva York: Walker and Company, pág. 100, ISBN 0-8027-1331-9, Sr.  1491363
26. Darling, David (2004), El libro universal de las matemáticas: desde Abracadabra hasta las paradojas de Zenón , Hoboken, Nueva Jersey: John Wiley & Sons, pág. 8, ISBN 0-471-27047-4, Sr.  2078978
27. Oxford English Dictionary, Oxford University Press, 2018, witch, n. ° 2, 4(e) , consultado el 3 de julio de 2018 , 1875 B. Williamson Elem. Treat. Integral Calculus vii. 173 Halla el área entre la bruja de Agnesi y su asíntota. ${\displaystyle xy^{2}=4a^{2}(2a-x)}$
28. Alexander, J. McKenzie (2012), "La teoría de la decisión se encuentra con la bruja de Agnesi", Journal of Philosophy , 109 (12): 712–727, doi :10.5840/jphil20121091233
29. Cupillari, Antonella ; DeThomas, Elizabeth (primavera de 2007), "Desenmascarando el comportamiento brujo de la función de Runge", Mathematics and Computer Education , 41 (2): 143–156, ProQuest  235858817
30. Spencer, Roy C. (septiembre de 1940), "Propiedades de la bruja de Agnesi: aplicación al ajuste de las formas de las líneas espectrales", Journal of the Optical Society of America , 30 (9): 415, Bibcode :1940JOSA...30..415S, doi :10.1364/josa.30.000415
31. Coppin, PA; Bradley, EF; Finnigan, JJ (abril de 1994), "Medidas de flujo sobre una cresta alargada y su dependencia de la estabilidad térmica: el campo medio", Meteorología de capa límite , 69 (1–2): 173–199, Bibcode :1994BoLMe..69..173C, doi :10.1007/bf00713302, S2CID  119956741, Una forma general útil para la forma de la colina es el llamado perfil de la "Bruja de Agnesi".
32. Snyder, William H.; Thompson, Roger S.; Eskridge, Robert E.; Lawson, Robert E.; Castro, Ian P.; Lee, JT; Hunt, Julian CR; Ogawa, Yasushi (marzo de 1985), "La estructura del flujo fuertemente estratificado sobre colinas: concepto de línea de corriente divisoria", Journal of Fluid Mechanics , 152 (–1): 249, Bibcode :1985JFM...152..249S, doi :10.1017/s0022112085000684, S2CID  123563729
33. Lamb, Kevin G. (febrero de 1994), "Simulaciones numéricas de flujo no viscoso estratificado sobre un obstáculo liso" (PDF) , Journal of Fluid Mechanics , 260 (–1): 1, Bibcode :1994JFM...260....1L, doi :10.1017/s0022112094003411, S2CID  49355530, archivado desde el original (PDF) el 6 de enero de 2014
34. Benjamin, T. Brooke (septiembre de 1967), "Ondas internas de forma permanente en fluidos de gran profundidad", Journal of Fluid Mechanics , 29 (3): 559, Bibcode :1967JFM....29..559B, doi :10.1017/s002211206700103x, S2CID  123065419
35. Noonan, Julie A.; Smith, Roger K. (septiembre de 1985), "Teorías de ondas internas lineales y débilmente no lineales aplicadas a las ondas 'morning glory'", Geophysical & Astrophysical Fluid Dynamics , 33 (1–4): 123–143, Bibcode :1985GApFD..33..123N, doi :10.1080/03091928508245426
36. Phillips, Dave (12 de septiembre de 2006), "Un maestro local y autor incorpora las matemáticas a sus libros", The Gazette
37. Radius – Witch Of Agnesi (Plutonium Records, 2002), Discogs , consultado el 28 de mayo de 2018

Enlaces externos

• "La bruja de Agnesi" en el índice de curvas famosas de MacTutor
• Weisstein, Eric W. , "La bruja de Agnesi", MathWorld
• Bruja de Agnesi de Chris Boucher basada en el trabajo de Eric W. Weisstein , The Wolfram Demonstrations Project .
• "La bruja de Agnesi" en "mathcurve"
• Lamb, Evelyn (28 de mayo de 2018), "Algunos de mis espacios favoritos: La bruja de Agnesi", Roots of Unity , Scientific American