stringtranslate.com

Cuerpo negro

Una aproximación física de un modelo de radiador de cuerpo negro se compone de una cámara de pirografito calentada y dispositivos periféricos que garantizan la estabilidad de la temperatura.
Radiador de cuerpo negro utilizado en el laboratorio CARLO en Polonia. Es una aproximación de un modelo descrito por la ley de Planck utilizado como estándar de irradiancia espectral .

A medida que la temperatura de un cuerpo negro disminuye, la intensidad de su radiación también disminuye y su pico se desplaza hacia longitudes de onda más largas. A modo de comparación, se muestra la ley clásica de Rayleigh-Jeans y su catástrofe ultravioleta .

Un cuerpo negro o blackbody es un cuerpo físico idealizado que absorbe toda la radiación electromagnética incidente , independientemente de la frecuencia o el ángulo de incidencia . La radiación emitida por un cuerpo negro en equilibrio térmico con su entorno se denomina radiación de cuerpo negro . El nombre de "cuerpo negro" se le da porque absorbe todos los colores de la luz. En cambio, un cuerpo blanco es uno con una "superficie rugosa que refleja todos los rayos incidentes de forma completa y uniforme en todas las direcciones". [1]

Un cuerpo negro en equilibrio térmico (es decir, a temperatura constante) emite radiación electromagnética de cuerpo negro. La radiación se emite según la ley de Planck , lo que significa que tiene un espectro que está determinado únicamente por la temperatura (ver figura a la derecha), no por la forma o la composición del cuerpo.

Un cuerpo negro ideal en equilibrio térmico tiene dos propiedades principales: [2]

  1. Es un emisor ideal: en cualquier frecuencia emite tanta o más energía radiativa térmica que cualquier otro cuerpo a la misma temperatura.
  2. Es un emisor difuso: medida por unidad de área perpendicular a la dirección, la energía se irradia isótropamente , independientemente de la dirección.

Los materiales reales emiten energía a una fracción (denominada emisividad ) de los niveles de energía de un cuerpo negro. Por definición, un cuerpo negro en equilibrio térmico tiene una emisividad ε = 1. Una fuente con una emisividad menor, independientemente de la frecuencia, suele denominarse cuerpo gris. [3] [4] La construcción de cuerpos negros con una emisividad lo más cercana posible a 1 sigue siendo un tema de interés actual. [5]

En astronomía , la radiación de las estrellas y los planetas a veces se caracteriza en términos de temperatura efectiva , la temperatura de un cuerpo negro que emitiría el mismo flujo total de energía electromagnética.

Definición

La idea de un cuerpo negro fue introducida originalmente por Gustav Kirchhoff en 1860 de la siguiente manera:

...la suposición de que pueden imaginarse cuerpos que, para espesores infinitamente pequeños, absorban completamente todos los rayos incidentes y no reflejen ni transmitan ninguno. Llamaré a tales cuerpos perfectamente negros o, más brevemente, cuerpos negros . [6]

Una definición más moderna omite la referencia a "espesores infinitamente pequeños": [7]

Ahora se define un cuerpo ideal, llamado cuerpo negro . Un cuerpo negro permite que toda la radiación incidente pase a través de él (no se refleja energía) y absorbe internamente toda la radiación incidente (no se transmite energía a través del cuerpo). Esto es cierto para la radiación de todas las longitudes de onda y para todos los ángulos de incidencia. Por lo tanto, el cuerpo negro es un absorbente perfecto para toda la radiación incidente. [8]

Idealizaciones

En esta sección se describen algunos conceptos desarrollados en relación con los cuerpos negros.

Una realización aproximada de un cuerpo negro como un pequeño agujero en un recinto aislado

Cavidad con un agujero

Un modelo ampliamente utilizado de una superficie negra es un pequeño agujero en una cavidad con paredes que son opacas a la radiación. [8] La radiación incidente en el agujero pasará a la cavidad y es muy poco probable que se vuelva a emitir si la cavidad es grande. La falta de cualquier reemisión significa que el agujero se está comportando como una superficie negra perfecta. El agujero no es una superficie negra perfecta; en particular, si la longitud de onda de la radiación incidente es mayor que el diámetro del agujero, parte se reflejará. De manera similar, incluso en perfecto equilibrio térmico, la radiación dentro de una cavidad de tamaño finito no tendrá un espectro de Planck ideal para longitudes de onda comparables o mayores que el tamaño de la cavidad. [9]

Supongamos que la cavidad se mantiene a una temperatura fija T y que la radiación atrapada en el interior del recinto está en equilibrio térmico con el recinto. El agujero en el recinto permitirá que escape algo de radiación. Si el agujero es pequeño, la radiación que entra y sale del agujero tiene un efecto insignificante sobre el equilibrio de la radiación dentro de la cavidad. Esta radiación que escapa se aproximará a la radiación de cuerpo negro que exhibe una distribución de energía característica de la temperatura T y no depende de las propiedades de la cavidad o del agujero, al menos para longitudes de onda más pequeñas que el tamaño del agujero. [9] Véase la figura en la Introducción para el espectro en función de la frecuencia de la radiación, que está relacionada con la energía de la radiación por la ecuación E = hf , con E = energía, h = constante de Planck , f = frecuencia.

En cualquier momento dado, la radiación en la cavidad puede no estar en equilibrio térmico, pero la segunda ley de la termodinámica establece que si no se altera, eventualmente alcanzará el equilibrio, [10] aunque el tiempo que toma hacerlo puede ser muy largo. [11] Normalmente, el equilibrio se alcanza por la absorción y emisión continua de radiación por el material en la cavidad o sus paredes. [12] [13] [14] [15] La radiación que ingresa a la cavidad se " termalizará " por este mecanismo: la energía se redistribuirá hasta que el conjunto de fotones alcance una distribución de Planck . El tiempo que toma la termalización es mucho más rápido con materia condensada presente que con materia enrarecida como un gas diluido. A temperaturas inferiores a miles de millones de Kelvin, las interacciones directas fotón-fotón [16] suelen ser insignificantes en comparación con las interacciones con la materia. [17] Los fotones son un ejemplo de un gas de bosones en interacción, [18] y como lo describe el teorema H , [19] en condiciones muy generales cualquier gas de bosones en interacción se acercará al equilibrio térmico.

Transmisión, absorción y reflexión.

El comportamiento de un cuerpo con respecto a la radiación térmica se caracteriza por su transmisión τ , absorción α y reflexión ρ .

El límite de un cuerpo forma una interfaz con su entorno, y esta interfaz puede ser rugosa o lisa. Una interfaz no reflectante que separa regiones con diferentes índices de refracción debe ser rugosa, porque las leyes de reflexión y refracción regidas por las ecuaciones de Fresnel para una interfaz lisa requieren un rayo reflejado cuando los índices de refracción del material y su entorno difieren. [20] Algunos tipos idealizados de comportamiento reciben nombres particulares:

Un cuerpo opaco es aquel que no transmite ninguna de la radiación que le llega, aunque parte puede reflejarse. [21] [22] Es decir, τ = 0 y α + ρ = 1.

Un cuerpo transparente es aquel que transmite toda la radiación que le llega, es decir, τ = 1 y α = ρ = 0.

Un cuerpo gris es aquel en el que α , ρ y τ son constantes para todas las longitudes de onda; este término también se utiliza para significar un cuerpo para el que α es independiente de la temperatura y la longitud de onda.

Un cuerpo blanco es aquel en el que toda la radiación incidente se refleja uniformemente en todas las direcciones: τ = 0, α = 0 y ρ = 1.

Para un cuerpo negro, τ = 0, α = 1 y ρ = 0. Planck ofrece un modelo teórico para cuerpos perfectamente negros, que según señaló no existen en la naturaleza: además de su interior opaco, tienen interfaces que son perfectamente transmisoras y no reflectantes. [23]

Los cuerpos negros perfectos de Kirchhoff

En 1860, Kirchhoff introdujo el concepto teórico de un cuerpo negro perfecto con una capa superficial completamente absorbente de un espesor infinitamente pequeño, pero Planck advirtió algunas restricciones severas a esta idea. Planck señaló tres requisitos para un cuerpo negro: el cuerpo debe (i) permitir que la radiación entre pero no se refleje; (ii) poseer un espesor mínimo adecuado para absorber la radiación incidente y evitar su reemisión; (iii) satisfacer limitaciones severas en materia de dispersión para evitar que la radiación entre y rebote. Como consecuencia, los cuerpos negros perfectos de Kirchhoff que absorben toda la radiación que incide sobre ellos no pueden realizarse en una capa superficial infinitamente delgada, e imponen condiciones a la dispersión de la luz dentro del cuerpo negro que son difíciles de satisfacer. [24] [25]

Realizaciones

La realización de un cuerpo negro se refiere a una encarnación física del mundo real. A continuación se indican algunos ejemplos.

Cavidad con un agujero

En 1898, Otto Lummer y Ferdinand Kurlbaum publicaron un relato de su fuente de radiación de cavidad. [26] Su diseño se ha utilizado prácticamente sin cambios para las mediciones de radiación hasta el día de hoy. Era un agujero en la pared de una caja de platino, dividido por diafragmas, con su interior ennegrecido con óxido de hierro. Fue un ingrediente importante para las mediciones progresivamente mejoradas que llevaron al descubrimiento de la ley de Planck. [27] [28] Una versión descrita en 1901 tenía su interior ennegrecido con una mezcla de óxidos de cromo, níquel y cobalto. [29] Véase también Hohlraum .

Materiales casi negros

Existe interés en los materiales tipo cuerpo negro para el camuflaje y en los materiales absorbentes de radar para la invisibilidad del radar. [30] [31] También tienen aplicación como colectores de energía solar y detectores térmicos infrarrojos. Como emisor perfecto de radiación, un material caliente con comportamiento de cuerpo negro crearía un calentador infrarrojo eficiente, particularmente en el espacio o en el vacío donde no hay calefacción por convección. [32] También son útiles en telescopios y cámaras como superficies antirreflejos para reducir la luz parásita y para recopilar información sobre objetos en áreas de alto contraste (por ejemplo, observación de planetas en órbita alrededor de sus estrellas), donde los materiales tipo cuerpo negro absorben la luz que proviene de fuentes equivocadas.

Se sabe desde hace tiempo que un recubrimiento de negro de humo hace que un cuerpo sea casi negro. Una mejora del negro de humo se encuentra en los nanotubos de carbono fabricados . Los materiales nanoporosos pueden lograr índices de refracción cercanos al del vacío, en un caso obteniendo una reflectancia promedio de 0,045%. [5] [33] En 2009, un equipo de científicos japoneses creó un material llamado nanoblack que está cerca de un cuerpo negro ideal, basado en nanotubos de carbono de pared simple alineados verticalmente . Este absorbe entre el 98% y el 99% de la luz entrante en el rango espectral desde las regiones ultravioleta hasta las de infrarrojo lejano. [32]

Otros ejemplos de materiales negros casi perfectos son el supernegro , preparado mediante el grabado químico de una aleación de níquel y fósforo , [34] las matrices de nanotubos de carbono alineadas verticalmente (como Vantablack ) y las nanoestructuras de carbono en forma de flor; [35] todas absorben el 99,9% de la luz o más.

Estrellas y planetas

Diagrama que compara las curvas de respuesta de los receptores de luz roja, verde y azul en los ojos humanos con las curvas aproximadas del cuerpo negro de varias estrellas: Antares (una supergigante roja ), el Sol (una enana amarilla ), Sirio (una estrella blanca de secuencia principal ), Spica (una estrella azul) y Gamma Velorum .

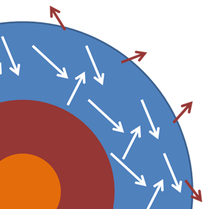
Una estrella o un planeta se modela a menudo como un cuerpo negro, y la radiación electromagnética emitida por estos cuerpos como radiación de cuerpo negro . La figura muestra una sección transversal muy esquemática para ilustrar la idea. La fotosfera de la estrella, donde se genera la luz emitida, se idealiza como una capa dentro de la cual los fotones de luz interactúan con el material de la fotosfera y alcanzan una temperatura común T que se mantiene durante un largo período de tiempo. Algunos fotones escapan y se emiten al espacio, pero la energía que se llevan es reemplazada por energía del interior de la estrella, de modo que la temperatura de la fotosfera es casi constante. Los cambios en el núcleo conducen a cambios en el suministro de energía a la fotosfera, pero tales cambios son lentos en la escala de tiempo que aquí nos interesa. Suponiendo que estas circunstancias se puedan realizar, la capa exterior de la estrella es algo análoga al ejemplo de un recinto con un pequeño agujero en él, con el agujero reemplazado por la transmisión limitada al espacio en el exterior de la fotosfera. Con todas estas suposiciones en su lugar, la estrella emite radiación de cuerpo negro a la temperatura de la fotosfera. [36]

Vista idealizada de la sección transversal de una estrella. La fotosfera contiene fotones de luz casi en equilibrio térmico y algunos escapan al espacio en forma de radiación cercana a la del cuerpo negro.

Utilizando este modelo se estima la temperatura efectiva de las estrellas, definida como la temperatura de un cuerpo negro que produce el mismo flujo superficial de energía que la estrella. Si una estrella fuera un cuerpo negro, la misma temperatura efectiva resultaría de cualquier región del espectro. Por ejemplo, las comparaciones en el rango B (azul) o V (visible) conducen al llamado índice de color BV , que aumenta cuanto más roja es la estrella, [37] siendo el Sol un índice de +0,648 ± 0,006. [38] Combinando los índices U (ultravioleta) y B se llega al índice UB , que se vuelve más negativo cuanto más caliente es la estrella y más radiación UV. Suponiendo que el Sol es una estrella de tipo G2 V, su índice UB es +0,12. [39] Los dos índices para dos tipos de secuencias de estrellas más comunes se comparan en la figura (diagrama) con la temperatura superficial efectiva de las estrellas si fueran cuerpos negros perfectos. Hay una correlación aproximada. Por ejemplo, para una medida dada del índice BV , las curvas de las dos secuencias más comunes de estrellas (la secuencia principal y las supergigantes) se encuentran por debajo del índice UB de cuerpo negro correspondiente que incluye el espectro ultravioleta, lo que muestra que ambas agrupaciones de estrellas emiten menos luz ultravioleta que un cuerpo negro con el mismo índice BV . Tal vez sea sorprendente que se ajusten a una curva de cuerpo negro tan bien como lo hacen, considerando que las estrellas tienen temperaturas muy diferentes a diferentes profundidades. [40] Por ejemplo, el Sol tiene una temperatura efectiva de 5780 K, [41] que puede compararse con la temperatura de su fotosfera (la región que genera la luz), que varía desde aproximadamente 5000 K en su límite exterior con la cromosfera hasta aproximadamente 9500 K en su límite interior con la zona de convección de aproximadamente 500 km (310 mi) de profundidad. [42]

Temperatura efectiva de un cuerpo negro comparada con el índice de color BV y UB de la secuencia principal y estrellas supergigantes en lo que se denomina un diagrama color-color . [43]

Agujeros negros

Un agujero negro es una región del espacio-tiempo de la que nada escapa. Alrededor de un agujero negro hay una superficie definida matemáticamente llamada horizonte de sucesos que marca el punto de no retorno . Se llama "negro" porque absorbe toda la luz que llega al horizonte, sin reflejar nada, lo que lo convierte casi en un cuerpo negro ideal [44] (la radiación con una longitud de onda igual o mayor que el diámetro del agujero puede no ser absorbida, por lo que los agujeros negros no son cuerpos negros perfectos). [45] Los físicos creen que para un observador externo, los agujeros negros tienen una temperatura distinta de cero y emiten radiación de cuerpo negro , radiación con un espectro de cuerpo negro casi perfecto, que finalmente se evapora . [46] El mecanismo de esta emisión está relacionado con las fluctuaciones del vacío en las que un par virtual de partículas se separa por la gravedad del agujero, un miembro es succionado hacia el agujero y el otro es emitido. [47] La ​​distribución de energía de la emisión se describe mediante la ley de Planck con una temperatura T :

donde c es la velocidad de la luz , ℏ es la constante de Planck reducida , k B es la constante de Boltzmann , G es la constante gravitacional y M es la masa del agujero negro. [48] Estas predicciones aún no han sido probadas ni observacionalmente ni experimentalmente. [49]

Radiación de fondo cósmico de microondas

La teoría del Big Bang se basa en el principio cosmológico , que establece que a gran escala el Universo es homogéneo e isótropo. Según la teoría, el Universo aproximadamente un segundo después de su formación era un cuerpo negro casi ideal en equilibrio térmico a una temperatura superior a 10 10 K. La temperatura disminuyó a medida que el Universo se expandió y la materia y la radiación en él se enfriaron. La radiación de fondo de microondas cósmica observada hoy es "el cuerpo negro más perfecto jamás medido en la naturaleza". [50] Tiene un espectro de Planck casi ideal a una temperatura de aproximadamente 2,7 K. Se aparta de la isotropía perfecta de la verdadera radiación del cuerpo negro por una anisotropía observada que varía con el ángulo en el cielo solo en aproximadamente una parte en 100.000.

Enfriamiento radiativo

Gráficos logarítmicos de longitud de onda de emisión máxima y excitación radiante frente a temperatura del cuerpo negro : las flechas rojas muestran que los cuerpos negros a 5780 K tienen una longitud de onda máxima de 501 nm y una excitación radiante de 63,3 MW/ m2.

La integración de la ley de Planck sobre todas las frecuencias proporciona la energía total por unidad de tiempo por unidad de superficie irradiada por un cuerpo negro mantenido a una temperatura T , y se conoce como ley de Stefan-Boltzmann :

donde σ es la constante de Stefan-Boltzmann , σ  ≈ 5,67 × 10 −8  W⋅m −2 ⋅K −4 ‍ [ 51] Para permanecer en equilibrio térmico a temperatura constante T , el cuerpo negro debe absorber o generar internamente esta cantidad de potencia P sobre el área dada A .

El enfriamiento de un cuerpo debido a la radiación térmica se aproxima a menudo utilizando la ley de Stefan-Boltzmann complementada con una emisividad de "cuerpo gris" ε ≤ 1 ( P / A = εσT 4 ). La tasa de disminución de la temperatura del cuerpo emisor se puede estimar a partir de la potencia radiada y la capacidad térmica del cuerpo . [52] Este enfoque es una simplificación que ignora los detalles de los mecanismos detrás de la redistribución del calor (que pueden incluir cambios en la composición, transiciones de fase o reestructuración del cuerpo) que ocurren dentro del cuerpo mientras se enfría, y asume que en cada momento en el tiempo el cuerpo se caracteriza por una sola temperatura. También ignora otras posibles complicaciones, como los cambios en la emisividad con la temperatura, [53] [54] y el papel de otras formas acompañantes de emisión de energía, por ejemplo, la emisión de partículas como los neutrinos. [55]

Si se supone que un cuerpo emisor caliente sigue la ley de Stefan-Boltzmann y se conocen su potencia de emisión P y su temperatura T , esta ley se puede utilizar para estimar las dimensiones del objeto emisor, porque la potencia total emitida es proporcional al área de la superficie emisora. De esta manera se encontró que los estallidos de rayos X observados por los astrónomos se originaron en estrellas de neutrones con un radio de unos 10 km, en lugar de agujeros negros como se conjeturó originalmente. [56] Una estimación precisa del tamaño requiere cierto conocimiento de la emisividad, en particular su dependencia espectral y angular. [57]

Véase también

Referencias

Citas

  1. ^ Planck 1914, págs. 9-10
  2. ^ Mahmoud Massoud (2005). "§2.1 Radiación de cuerpo negro". Ingeniería de termofluidos: termodinámica, mecánica de fluidos y transferencia de calor . Springer. pág. 568. ISBN 978-3-540-22292-7.
  3. ^ La emisividad de una superficie depende en principio de la frecuencia, el ángulo de visión y la temperatura. Sin embargo, por definición, la radiación de un cuerpo gris es simplemente proporcional a la de un cuerpo negro a la misma temperatura, por lo que su emisividad no depende de la frecuencia (o, equivalentemente, de la longitud de onda). Véase Massoud Kaviany (2002). "Figura 4.3(b): Comportamientos de una superficie gris (sin dependencia de la longitud de onda), difusa (sin dependencia direccional) y opaca (sin transmisión)". Principios de transferencia de calor . Wiley-IEEE. pág. 381. ISBN 978-0-471-43463-4.y Ronald G. Driggers (2003). Enciclopedia de ingeniería óptica, volumen 3. CRC Press. pág. 2303. ISBN 978-0-8247-4252-2.
  4. ^ Algunos autores describen las fuentes de radiación infrarroja con una emisividad mayor que aproximadamente 0,99 como un cuerpo negro. Véase "¿Qué es un cuerpo negro y la radiación infrarroja?". Pestaña Educación/Referencia . Electro Optical Industries, Inc. 2008. Archivado desde el original el 7 de marzo de 2016 . Consultado el 10 de junio de 2019 .
  5. ^ ab Chun, Ai Lin (2008). "Más negro que el negro". Nature Nanotechnology . doi : 10.1038/nnano.2008.29 .
  6. ^ Traducido por F. Guthrie de Annalen der Physik : 109 , 275-301 (1860): G. Kirchhoff (julio de 1860). "Sobre la relación entre los poderes de radiación y absorción de diferentes cuerpos para la luz y el calor". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science . 20 (130).
  7. ^ Planck abandonó la noción de una capa infinitamente delgada. Véase Planck 1914, p. 10, nota al pie 2.
  8. ^ ab Siegel, Robert; Howell, John R. (2002). Transferencia de calor por radiación térmica; Volumen 1 (4.ª ed.). Taylor & Francis. pág. 7. ISBN 978-1-56032-839-1.
  9. ^ ab Las correcciones del espectro surgen en relación con las condiciones de contorno en las paredes, la curvatura y la topología, en particular para longitudes de onda comparables a las dimensiones de la cavidad; véase Roger Dale Van Zee; J. Patrick Looney (2002). Cavity-enhanced spectroscopies. Academic Press. p. 202. ISBN 978-0-12-475987-9.
  10. ^ Clement John Adkins (1983). "§4.1 La función de la segunda ley". Termodinámica del equilibrio (3.ª ed.). Cambridge University Press. pág. 50. ISBN 978-0-521-27456-2.
  11. ^ En casos simples, la aproximación al equilibrio está regida por un tiempo de relajación . En otros, el sistema puede "quedarse estancado" en un estado metaestable , como afirma Adkins (1983) en la página 10. Para otro ejemplo, véase Michel Le Bellac; Fabrice Mortessagne; Ghassan George Batrouni (2004). Equilibrium and non-equilibrium statistical thermodynamics. Cambridge University Press. p. 8. ISBN 978-0521821438.
  12. ^ La aproximación al equilibrio térmico de la radiación en la cavidad puede catalizarse añadiendo un pequeño trozo de materia capaz de radiar y absorber en todas las frecuencias. Véase Peter Theodore Landsberg (1990). Thermodynamics and statistical mechanics (Reimpresión de Oxford University Press 1978 ed.). Courier Dover Publications. p. 209. ISBN 978-0-486-66493-4.
  13. ^ Planck 1914, pág. 44, §52
  14. ^ Loudon 2000, Capítulo 1
  15. ^ Mandel y Wolf 1995, Capítulo 13
  16. ^ Robert Karplus* y Maurice Neuman, "La dispersión de la luz por la luz", Phys. Rev. 83, 776–784 (1951)
  17. ^ Ludwig Bergmann; Clemens Schäfer; Heinz Niedrig (1999). Óptica de ondas y partículas. Walter de Gruyter. pag. 595.ISBN​ 978-3-11-014318-8Debido a que la interacción de los fotones entre sí es insignificante, se necesita una pequeña cantidad de materia para establecer el equilibrio termodinámico de la radiación de calor.
  18. ^ Los bosones fundamentales son el fotón , los bosones vectoriales de la interacción débil , el gluón y el gravitón . Véase Allan Griffin; DW Snoke ; S. Stringari (1996). Condensación de Bose-Einstein. Cambridge University Press. p. 4. ISBN 978-0-521-58990-1.
  19. ^ Richard Chace Tolman (2010). "§103: Cambio de H con el tiempo como resultado de colisiones". Los principios de la mecánica estadística (reimpresión de la edición de 1938 de Oxford University Press). Dover Publications. pp. 455 y siguientes . ISBN 978-0-486-63896-6... podemos definir una cantidad adecuada H para caracterizar la condición de un gas que [exhibirá] una tendencia a disminuir con el tiempo como resultado de colisiones, a menos que la distribución de las moléculas [ya sea la de] equilibrio. (p. 458)
  20. ^ Paul A. Tipler (1999). "Intensidad relativa de la luz reflejada y transmitida". Física para científicos e ingenieros, partes 1-35; parte 39 (4.ª ed.). Macmillan. pág. 1044. ISBN 978-0-7167-3821-3.
  21. ^ Massoud Kaviany (2002). "Figura 4.3(b) Propiedades de radiación de una superficie opaca". Principios de transferencia de calor . Wiley-IEEE. pág. 381. ISBN 978-0-471-43463-4.
  22. ^ BA Venkanna (2010). "§10.3.4 Absortividad, reflectividad y transmisividad". Fundamentos de transferencia de calor y masa . PHI Learning Pvt. Ltd., págs. 385-386. ISBN 978-81-203-4031-2.
  23. ^ Planck 1914, pág. 10
  24. ^ Planck 1914, págs. 9-10, §10
  25. ^ Kirchhoff 1860c
  26. ^ Lummer y Kurlbaum 1898
  27. ^ Se puede encontrar una extensa discusión histórica en Mehra, Jagdish ; Rechenberg, Helmut (2000). El desarrollo histórico de la teoría cuántica. Springer. pp. 39 y siguientes . ISBN . 978-0-387-95174-4.
  28. ^ Kangro 1976, pág. 159
  29. ^ Lummer y Kurlbaum 1901
  30. ^ CF Lewis (junio de 1988). "Los materiales mantienen un perfil bajo" (PDF) . Ingeniería mecánica : 37–41.[ enlace muerto permanente ]
  31. ^ Bradley Quinn (2010). Textile Futures. Berg. pág. 68. ISBN 978-1-84520-807-3.
  32. ^ ab K. Mizuno; et al. (2009). "Un absorbedor de cuerpo negro a partir de nanotubos de carbono de pared simple alineados verticalmente". Actas de la Academia Nacional de Ciencias . 106 (15): 6044–6077. Bibcode :2009PNAS..106.6044M. doi : 10.1073/pnas.0900155106 . PMC 2669394 . PMID  19339498. 
  33. ^ Zu-Po Yang; et al. (2008). "Observación experimental de un material extremadamente oscuro creado con una matriz de nanotubos de baja densidad". Nano Letters . 8 (2): 446–451. Bibcode :2008NanoL...8..446Y. doi :10.1021/nl072369t. PMID  18181658. S2CID  7412160.
  34. ^ Véase la descripción del trabajo de Richard Brown y sus colegas del Laboratorio Nacional de Física del Reino Unido: Mick Hamer (6 de febrero de 2003). "Los mini cráteres son la clave del 'negro más negro jamás visto'". New Scientist .
  35. ^ Ghai, Viney; Singh, Harpreet; Agnihotri, Prabhat K. (2019). "Nanotubos de carbono similares al diente de león para superficies negras casi perfectas". ACS Applied Nano Materials . 2 (12): 7951–7956. doi :10.1021/acsanm.9b01950. S2CID  213017898.
  36. ^ Simon F. Green; Mark H. Jones; S. Jocelyn Burnell (2004). Una introducción al sol y las estrellas. Cambridge University Press. pp. 21–22, 53. ISBN 978-0-521-54622-5Una fuente en la que los fotones tienen muchas más probabilidades de interactuar con el material dentro de la fuente que de escapar es una condición para la formación de un espectro de cuerpo negro .
  37. ^ David H. Kelley; Eugene F. Milone; Anthony F. (FRW) Aveni (2011). Explorando los cielos antiguos: un estudio de la astronomía antigua y cultural (2.ª ed.). Springer. pág. 52. ISBN 978-1-4419-7623-9.
  38. ^ David F Gray (febrero de 1995). "Comparación del Sol con otras estrellas a lo largo de la coordenada de temperatura". Publicaciones de la Sociedad Astronómica del Pacífico . 107 : 120–123. Bibcode :1995PASP..107..120G. doi : 10.1086/133525 .
  39. ^ M Golay (1974). "Tabla IX: Índices UB". Introducción a la fotometría astronómica . Springer. pág. 82. ISBN 978-90-277-0428-3.
  40. ^ Lawrence Hugh Aller (1991). Átomos, estrellas y nebulosas (3.ª ed.). Cambridge University Press. pág. 61. ISBN 978-0-521-31040-6.
  41. ^ Kenneth R. Lang (2006). Fórmulas astrofísicas, volumen 1 (3.ª ed.). Birkhäuser. pág. 23. ISBN 978-3-540-29692-8.
  42. ^ B. Bertotti; Paolo Farinella; David Vokrouhlický (2003). "Figura 9.2: El perfil de temperatura en la atmósfera solar". Nuevas vistas del sistema solar . Springer. pág. 248. ISBN 978-1-4020-1428-4.
  43. ^ Figura modelada a partir de E. Böhm-Vitense (1989). "Figura 4.9". Introducción a la astrofísica estelar: observaciones y datos estelares básicos . Cambridge University Press. pág. 26. ISBN 978-0-521-34869-0.
  44. ^ Schutz, Bernard (2004). Gravedad desde el grupo hacia arriba: una guía introductoria a la gravedad y la relatividad general (1.ª ed.). Cambridge University Press. pág. 304. ISBN 978-0-521-45506-0.
  45. ^ PCW Davies (1978). «Termodinámica de los agujeros negros» (PDF) . Rep Prog Phys . 41 (8): 1313–1355. Bibcode :1978RPPh...41.1313D. doi :10.1088/0034-4885/41/8/004. S2CID  250916407. Archivado desde el original (PDF) el 10 de mayo de 2013.
  46. ^ Robert M Wald (2005). "La termodinámica de los agujeros negros". En Andrés Gomberoff; Donald Marolf (eds.). Lecciones sobre gravedad cuántica . Springer Science & Business Media . págs. 1–38. ISBN 978-0-387-23995-8.
  47. ^ Bernard J Carr y Steven B Giddings (2008). "Capítulo 6: Agujeros negros cuánticos". Más allá de la física extrema: ciencia de vanguardia. Rosen Publishing Group, Scientific American (COR). pág. 30. ISBN 978-1-4042-1402-6.
  48. ^ Valeri P. Frolov; Andrei Zelnikov (2011). "Ecuación 9.7.1". Introducción a la física de agujeros negros . Oxford University Press. pág. 321. ISBN 978-0-19-969229-3.
  49. ^ Robert M Wald (2005). "La termodinámica de los agujeros negros (pp. 1–38)". En Andrés Gomberoff; Donald Marolf (eds.). Lecciones sobre gravedad cuántica . Springer Science & Business Media . p. 28. ISBN 978-0-387-23995-8... ningún resultado sobre la termodinámica de los agujeros negros ha sido sometido a ninguna prueba experimental u observacional...
  50. ^ White, M. (1999). "Anisotropías en el CMB" (PDF) . Actas de la reunión de Los Ángeles, DPF 99. UCLA .Véase también arXive.org.
  51. ^ "Valor CODATA 2022: constante de Stefan–Boltzmann". Referencia del NIST sobre constantes, unidades e incertidumbre . NIST . Mayo de 2024. Consultado el 18 de mayo de 2024 .
  52. ^ Srivastava MK (2011) ofrece un ejemplo sencillo : "Refrigeración por radiación". The Person Guide to Objective Physics for the IIT-JEE . Pearson Education India. pág. 610. ISBN 978-81-317-5513-6.
  53. ^ M Vollmer; KP Mõllmann (2011). "Figura 1.38: Algunos ejemplos de dependencia de la temperatura de la emisividad para diferentes materiales". Imágenes térmicas infrarrojas: fundamentos, investigación y aplicaciones . John Wiley & Sons. pág. 45. ISBN 978-3-527-63087-5.
  54. ^ Robert Osiander; M. Ann Garrison Darrin; John Champion (2006). MEMS y microestructuras en aplicaciones aeroespaciales. CRC Press. pág. 187. ISBN 978-0-8247-2637-9.
  55. ^ Krishna Rajagopal; Frank Wilczek (2001). "6.2 Coling por emisiones de neutrinos (pp. 2135-2136) – La física de la materia condensada de la QCD". En Mikhail A. Shifman (ed.). En la frontera de la física de partículas: Manual de QCD (Con motivo del 75.º cumpleaños del profesor Boris Ioffe) . Vol. 3. Singapur: World Scientific . págs. 2061–2151. arXiv : hep-ph/0011333v2 . CiteSeerX 10.1.1.344.2269 . doi :10.1142/9789812810458_0043. ISBN .  978-981-02-4969-4. S2CID  13606600. Durante los primeros 10 5–6 años de su vida, el enfriamiento de una estrella de neutrones está gobernado por el equilibrio entre la capacidad térmica y la pérdida de calor por emisión de neutrinos. ... Tanto el calor específico C V como la tasa de emisión de neutrinos L ν están dominados por la física dentro de T de la superficie de Fermi. ... La estrella se enfriará rápidamente hasta que su temperatura interior sea T  <  T c  ~ ∆ , momento en el que el núcleo de materia de quarks se volverá inerte y la historia de enfriamiento posterior estará dominada por la emisión de neutrinos de la fracción de materia nuclear de la estrella.
  56. ^ Walter Lewin; Warren Goldstein (2011). "¡Explosiones de rayos X!". Por amor a la física. Simon and Schuster. pp. 251 y siguientes. ISBN 978-1-4391-0827-7.
  57. ^ TE Strohmayer (2006). "Estructura de la estrella de neutrones y física fundamental". En John W. Mason (ed.). Actualización de la astrofísica, volumen 2. Birkhäuser. pág. 41. ISBN 978-3-540-30312-1.

Bibliografía

Enlaces externos