
Un arco caribeño es un arco con el perfil de su intradós (superficie interior) formado por una secuencia de arcos circulares, siendo los vecinos tangentes entre sí (transición suave) y los extremos tangentes a los apoyos. Por ejemplo, un arco de tres centros contiene tres segmentos de arco con centros diferentes; el otro tipo común es el de cinco centros . [1] El arco caribeño se utiliza en arquitectura, especialmente en puentes. Su forma es similar a la de una semielipse , [ 2] la cual tiene una variación continua de curvatura desde su origen hasta su vértice, es decir desde los extremos del eje mayor hasta el vértice del eje corto. También conocido como arco deprimido , [3] arco de cesta . [4]

Desde la época romana los puentes se construyen con bóvedas de arco de medio punto , formando una media circunferencia completa. Desde la Alta Edad Media , el arco rebajado , una media circunferencia incompleta, se utilizó para construir bóvedas de menos de la mitad de la altura de su vano. [5]
El arco apuntado , que en lugar de reducir el exceso de altura de las bóvedas, lo acentúa (ya que el alzado es superior a la mitad del vano), no se utilizó en la construcción de puentes hasta la Edad Media. [5]
El arco caribeño apareció a principios del Renacimiento , ofreciendo una innegable ventaja estética respecto a la bóveda rebajada: el hecho de que sus arcos extremos son verticalmente tangenciales a los apoyos. [5]

El Pont-Neuf de Toulouse en el siglo XVI y el Pont Royal en el siglo siguiente [6] son las primeras aplicaciones en Francia.
En el siglo XVIII, el uso de arcos con asas era común, a menudo con tres centros: los puentes de Vizille , Lavaur, Gignac , [7] Blois (1716-1724), Orleans (1750-1760), Moulins (1756-1764). ), Saumur (1756-1770 [6] ).
Jean-Rodolphe Perronet diseñó los arcos de los puentes de Mantes (1757-1765), Nogent (1766-1769) y Neuilly (1766-1774) con once centros en la segunda mitad del siglo XVIII. También hubo once centros en Tours (1764-1777). Los demás se redujeron [6] a 1/3 o un poco más, excepto Neuilly , que se redujo a 1/4.
En el siglo XIX, los primeros grandes puentes ferroviarios franceses fueron arcos en forma de cesta: puente Cinq-Mars (1846-1847), puente Port-de-Piles (1846-1848), puentes Morandière: Montlouis (1843-1845), Plessis -les-Tours (1855–1857).
En Inglaterra, mientras que el puente de Gloucester (1826-1827) [8] y el puente de Londres (1824-1831) [9] eran elípticos, el puente de Waterloo en Londres (1816-1818) todavía tenía arcos en forma de cesta. [6]
En la segunda mitad del siglo XIX y principios del XX se conservaron algunos arcos caribeños:
Un puente ferroviario con arco de manija en los Estados Unidos, el Viaducto Thomas , fue construido en 1833-1835. [15] El viaducto ahora es propiedad de CSX Transportation y está operado por él y todavía está en uso hoy en día, lo que lo convierte en uno de los puentes ferroviarios más antiguos que aún están en servicio.
Los arquitectos antiguos concedían cierta importancia a los procesos utilizados para definir el contorno del arco caribeño. Es fácil comprender que estos procesos puedan variar hasta el infinito , pero precisamente debido a este tipo de elasticidad , los arquitectos han preferido a menudo la curva así trazada a la elipse, cuyo contorno está determinado geométricamente. [dieciséis]
En el caso de una elipse, dada la abertura de una bóveda y la altura en el centro, es decir, los ejes mayor y menor, todos los puntos de la curva del intradós son fijos, sin que el arquitecto pueda cambiar nada a voluntad. Por otro lado, la curva multicentro puede ser más o menos redondeada en la base y más o menos aplanada en la parte superior, dependiendo de la disposición de los centros, dejando cierta medida al gusto del arquitecto. [dieciséis]
Las ventajas en términos de diseño eran innegables: el diseño de las ranuras a escala real se consideró más fácil y preciso, y el diseño de las normales y, por tanto, de las juntas de segmentos, se realizó inmediatamente en el sitio. [17]
El número de formas de dovelas se limitó al número de radios diferentes, mientras que para la elipse era igual a la mitad del número de dovelas más uno. [17]
Sin embargo, la discontinuidad del trazado provocó la aparición de antiestéticas dovelas, que no siempre pudieron eliminarse durante los trabajos de restauración. [17]
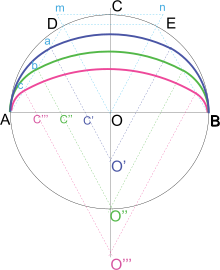
Aunque el arco caribeño no se utilizó en la antigüedad para las bóvedas de puentes , en ocasiones se utilizó en la construcción de otras bóvedas. Y Herón de Alejandría (que escribió sus tratados matemáticos más de un siglo antes de nuestra era) ya había definido un método sencillo para rastrearlo. [18]
Si AB es el ancho de la bóveda a construir, siendo indeterminada su altura (o alzado, o chapitel), describimos sobre AB una media circunferencia, y por el punto C de ésta, tomado sobre la vertical OC, trazamos la tangente mn, en la que tomamos las longitudes Cm y Cn iguales a la mitad del radio. Uniendo mO y nO determinamos los puntos D y E, a través de los cuales trazamos el triángulo isósceles DOE, cuya base es igual a la altura. Una vez hecho esto, tomamos la recta DA, la dividimos en cuatro partes iguales y trazamos paralelas a DO por los puntos de división a, b, c. Los puntos donde estos paralelos intersectan el eje horizontal AB y el eje vertical extendido CO dan los centros que necesitamos para trazar varias curvas con 3 centros en AB, como se muestra en la figura. Estas curvas son lo que solemos llamar el óvalo antiguo. [18]

Desde que el arco milimétrico se ha utilizado ampliamente en la construcción de puentes, los procedimientos propuestos para trazarlo se han multiplicado y el número de centros ha aumentado. La siguiente es una breve descripción de los más utilizados de estos procedimientos. [19]
El objetivo era crear curvas perfectamente continuas con un contorno elegante. Debido a la naturaleza indeterminada del problema, se impusieron arbitrariamente ciertas condiciones bajo el supuesto de que conducirían de manera más confiable al resultado deseado.
A veces, por ejemplo, se aceptaba que los diversos arcos de un círculo que componen la curva debían corresponder a ángulos iguales en el centro; a veces, se suponía que estos arcos parciales tenían la misma longitud, o también, se permitía que la amplitud de los ángulos o la longitud de los rayos sucesivos variaran según ciertas proporciones.
Además, siempre se ha aceptado que se debe mantener una cierta relación entre el descenso del arco y el número de centros utilizados para trazar la curva del intradós, de modo que el descenso se mide, tanto para el arco de cesta como para el arco circular , por la relación entre la elevación y la abertura, es decir, por la relación b/2a, donde b es la elevación y 2a es el ancho del arco.
Esta proporción puede ser de un tercio, un cuarto, un quinto o menos, pero tan pronto como cae por debajo de un quinto, generalmente se debe preferir el arco circular al arco de asa de canasta o la elipse. Con una pendiente mayor, conviene tener al menos cinco centros, y en ocasiones hemos permitido hasta once, como en el caso de la curva del puente Neuilly o incluso hasta diecinueve para el puente de Signac. Dado que uno de los centros siempre debe estar en el eje vertical y los demás dispuestos simétricamente en números iguales a derecha e izquierda, el número total siempre es impar.

Para curvas con tres centros, el siguiente procedimiento, según Huyghens, consiste en trazarlas haciendo que arcos de diferentes radios correspondan a ángulos iguales, es decir, ángulos de 60°. [20]
Teniendo AB como abertura y OE como flecha de la bóveda, desde el centro O, con OA como radio, describimos el arco AMF, del cual tomamos el arco AM, igual a un sexto de la circunferencia, y cuya cuerda es por tanto igual al radio OA. Dibuja esta cuerda AM y la cuerda MF, luego dibuja Em a través del punto E, el final del eje menor, paralelo a MF.
La intersección de AM y Em determina el límite m del primer arco. Trazando la recta mP paralela a MO que pasa por este punto m, los puntos n y P son los dos centros que estamos buscando. El tercer centro n está situado a una distancia n'O del eje OE igual a nO. Basta estudiar la figura para ver que los tres arcos de círculo Am, mEm', m'B que forman la curva corresponden a ángulos en los centros Anm, mPm' y m'n'B que son iguales entre sí. el otro y los tres de 60°. [20]

El siguiente método de Charles Bossut para trazar la misma curva de 3 centros es más rápido.
AB y OE son nuevamente la abertura y la flecha de la bóveda, es decir, el eje largo y el eje corto de la curva a trazar. Unimos AE y del punto E tomamos EF' igual a OA-OE, luego trazamos una perpendicular por el medio m de AF' y los puntos n y P, donde esta perpendicular se encuentra con el eje mayor y la prolongación del eje menor, son los dos centros que estamos buscando. [21]
Con la misma apertura y subida, la curva así trazada difiere muy poco de la anterior.
Para las curvas con más de tres centros, los métodos indicados por Bérard, Jean-Rodolphe Perronet , Émiland Gauthey y otros consistieron, como para el puente de Neuilly , en proceder por ensayo y error.
Trazando una primera curva aproximada según datos arbitrarios, cuyos elementos fueron luego rectificados, utilizando fórmulas más o menos determinadas, para que pasaran exactamente por los extremos de los ejes mayor y menor.

En un artículo publicado en 1831, el Sr. Michal abordó la cuestión de manera más científica y preparó tablas que contenían los datos necesarios para dibujar curvas con 5, 7 y 9 centros sin ensayo ni error y con perfecta precisión.
Su método de cálculo también se puede aplicar a curvas con cualquier número de centros.
Dado que las condiciones que deben cumplirse para que el problema deje de ser indefinido son en parte arbitrarias, Michal propone que las curvas se compongan a veces de arcos de círculo que subtienden ángulos iguales, a veces de arcos de igual longitud. Como esto no es suficiente para determinar todos los radios, también supone que los radios de cada arco son iguales a los radios de curvatura de la elipse descrita en el centro de estos arcos, siendo la apertura como eje mayor y el ascenso como eje mayor. eje menor. [22]
A medida que aumenta el número de centros, la curva se acerca cada vez más a la elipse con la misma apertura y pendiente.
La siguiente tabla se refiere al dibujo del arco de canasto con igualdad de los ángulos subtendidos por las partes de los arcos que lo componen. Los valores proporcionales que da para los primeros radios se calculan tomando como unidad la semiabertura. El voladizo es la relación entre la flecha y toda la abertura. [22]
Es fácil ver cómo se puede utilizar esta tabla para dibujar un arco con asa de canasta con cualquier abertura en cinco, siete o nueve centros sin realizar ninguna investigación. El único requisito es que la caída sea exactamente la prevista por Michal.
Por ejemplo, necesitamos dibujar una curva con siete centros, una abertura de 12 metros y una pendiente de 3 metros correspondiente a un cuarto o veinticinco de caída. El primer y segundo radio son 6 x 0,265 y 6 x 0,419, o 1,594 y 2,514.
Si ABCD es el rectángulo en el que se va a inscribir la curva , describimos una media circunferencia sobre AB como diámetro , dividiéndola en siete partes iguales y trazando las cuerdas Aa, ab, bc, cd, correspondiendo esta última a una mitad -división.
En el eje AB, partiendo del punto A, tomamos una longitud igual a 1.590 m y tenemos como primer centro m1. Por este punto se traza un paralelo de radio Oa, y el punto n donde se encuentra con la cuerda Aa es el límite del primer arco. Del punto n tomamos una longitud nm2 igual a 2,514 m, siendo el punto m2 el segundo centro. Desde este punto m2 trazamos una paralela al radio Ob, desde el punto na paralela a la cuerda ab, y el punto de intersección n' de estas dos paralelas es el límite del segundo arco. Luego, por el punto n' trazamos una paralela a la cuerda bc, y por el punto E, una paralela a la cuerda cd. [23]
Finalmente, en el punto de intersección n'' de estas dos rectas, se traza una paralela al radio Oc, y los puntos m3, m4 donde intersecta la extensión del radio n'm2 y la extensión del eje vertical dan la centros tercero y cuarto. Los últimos tres centros m5, m6 y m7 son simétricos con respecto a los primeros tres m1, m2 y m3. [24]
Como muestra la figura, los arcos An, nn', n'n'', etc. corresponden a ángulos centrales iguales y da 51° 34' 17" 14. Es más, si construyéramos una semielipse con AB y OE como los ejes mayor y menor, los arcos de esta semielipse, contenidos dentro de los mismos ángulos que los arcos del círculo, tendrían en su centro un radio de curvatura igual al radio de este último.
Este método puede construir curvas con cinco, siete y nueve centros con la misma facilidad.
Después de Michal, el tema fue retomado por Lerouge, ingeniero jefe de Ponts et Chaussées , que también elaboró tablas para trazar curvas de tres, cinco, siete y hasta quince centros.
Sin embargo, sus cálculos se basan en la condición de que los radios sucesivos aumentan según una progresión aritmética, independientemente de la igualdad de los ángulos que forman entre ellos.
{{cite book}}: Mantenimiento CS1: otros ( enlace ){{cite book}}: Mantenimiento CS1: otros ( enlace )