En el procesamiento de señales y disciplinas relacionadas, el aliasing es la superposición de componentes de frecuencia resultantes de una frecuencia de muestreo inferior a la frecuencia de Nyquist . Esta superposición produce distorsión o artefactos cuando la señal se reconstruye a partir de muestras, lo que hace que la señal reconstruida difiera de la señal continua original. El aliasing que se produce en señales muestreadas en el tiempo, por ejemplo en audio digital o el efecto estroboscópico , se denomina aliasing temporal . El aliasing en señales muestreadas espacialmente (por ejemplo, patrones muaré en imágenes digitales ) se denomina aliasing espacial .
El aliasing generalmente se evita aplicando filtros de paso bajo o filtros anti-aliasing (AAF) a la señal de entrada antes del muestreo y al convertir una señal de una frecuencia de muestreo más alta a una más baja. Luego se debe utilizar un filtrado de reconstrucción adecuado al restaurar la señal muestreada al dominio continuo o al convertir una señal de una frecuencia de muestreo más baja a una más alta. Para el anti-aliasing espacial , los tipos de anti-aliasing incluyen anti-aliasing aproximado rápido (FXAA), anti-aliasing multimuestra y supermuestreo .
Cuando se visualiza una imagen digital, se lleva a cabo una reconstrucción mediante un dispositivo de visualización o impresora, así como mediante los ojos y el cerebro. Si los datos de la imagen se procesan incorrectamente durante el muestreo o la reconstrucción, la imagen reconstruida será diferente de la imagen original y se verá una imagen con un alias.
Un ejemplo de aliasing espacial es el patrón muaré observado en una imagen mal pixelada de una pared de ladrillos. Las técnicas de anti-aliasing espacial evitan este tipo de pixelizaciones deficientes. El aliasing puede ser causado por la etapa de muestreo o por la etapa de reconstrucción; estas pueden distinguirse llamando aliasing de muestreo. Prealiasing y aliasing de reconstrucción postalización. [1]
El aliasing temporal es un problema importante en el muestreo de señales de vídeo y audio. La música, por ejemplo, puede contener componentes de alta frecuencia que son inaudibles para los humanos. Si se muestrea una pieza musical a 32.000 muestras por segundo (Hz), cualquier componente de frecuencia igual o superior a 16.000 Hz (la frecuencia de Nyquist para esta frecuencia de muestreo) provocará aliasing cuando la música se reproduzca mediante un convertidor digital a analógico (DAC). Las frecuencias altas de la señal analógica aparecerán como frecuencias más bajas (alias incorrecto) en la muestra digital grabada y, por lo tanto, no podrán ser reproducidas por el DAC. Para evitarlo, se utiliza un filtro anti-aliasing para eliminar los componentes por encima de la frecuencia de Nyquist antes del muestreo.
En el vídeo o la cinematografía, el aliasing temporal resulta de la frecuencia de imagen limitada y causa el efecto de rueda de carreta , por el cual una rueda con radios parece girar demasiado lentamente o incluso hacia atrás. El aliasing ha cambiado su frecuencia aparente de rotación. Una inversión de dirección puede describirse como una frecuencia negativa . Las frecuencias de aliasing temporal en vídeo y cinematografía están determinadas por la frecuencia de imagen de la cámara, pero la intensidad relativa de las frecuencias aliasing está determinada por el tiempo de obturación (tiempo de exposición) o el uso de un filtro de reducción de aliasing temporal durante la filmación. [2] [ ¿ Fuente poco confiable? ]
Al igual que la cámara de vídeo, la mayoría de los esquemas de muestreo son periódicos; es decir, tienen una frecuencia de muestreo característica en el tiempo o en el espacio. Las cámaras digitales proporcionan una cierta cantidad de muestras ( píxeles ) por grado o por radián, o muestras por mm en el plano focal de la cámara. Las señales de audio se muestrean ( digitalizan ) con un convertidor analógico a digital , que produce una cantidad constante de muestras por segundo. Algunos de los ejemplos más dramáticos y sutiles de aliasing ocurren cuando la señal que se muestrea también tiene contenido periódico.
Las señales reales tienen una duración finita y su contenido de frecuencia, tal como se define por la transformada de Fourier , no tiene límite superior. Siempre se produce cierta cantidad de aliasing cuando se muestrean dichas funciones. Las funciones cuyo contenido de frecuencia está acotado ( limitado por banda ) tienen una duración infinita en el dominio del tiempo. Si se muestrea a una velocidad suficientemente alta, determinada por el ancho de banda , la función original puede, en teoría, reconstruirse perfectamente a partir del conjunto infinito de muestras.
A veces, el aliasing se utiliza intencionalmente en señales sin contenido de baja frecuencia, llamadas señales de paso de banda . El submuestreo , que crea aliasing de baja frecuencia, puede producir el mismo resultado, con menos esfuerzo, que desplazar la señal a frecuencias más bajas antes de muestrear a la tasa más baja. Algunos canalizadores digitales explotan el aliasing de esta manera para lograr eficiencia computacional. [3] (Ver Muestreo (procesamiento de señales) , Tasa de Nyquist (relativa al muestreo) y Banco de filtros ).

Las sinusoides son un tipo importante de función periódica, ya que las señales realistas suelen modelarse como la suma de muchas sinusoides de diferentes frecuencias y amplitudes (por ejemplo, con una serie o transformada de Fourier ). Comprender lo que el aliasing hace con las sinusoides individuales es útil para entender qué sucede con su suma.
Al muestrear una función en la frecuencia f s (intervalos 1/ f s ), las siguientes funciones de tiempo ( t ) producen conjuntos idénticos de muestras: {sin(2π( f+Nf s ) t + φ), N = 0, ±1, ±2, ±3,... }. Un espectro de frecuencia de las muestras produce respuestas igualmente fuertes en todas esas frecuencias. Sin información colateral, la frecuencia de la función original es ambigua. Por lo tanto, se dice que las funciones y sus frecuencias son alias entre sí. Observando la identidad trigonométrica :
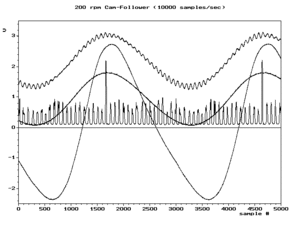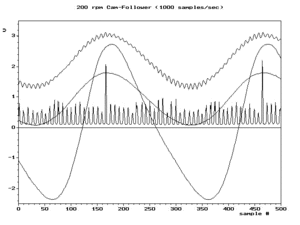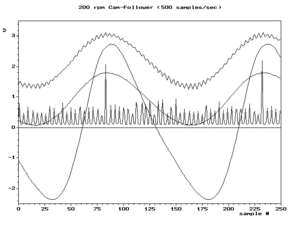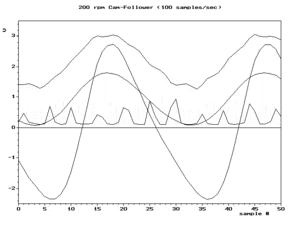
Podemos escribir todas las frecuencias de alias como valores positivos: . Por ejemplo, una instantánea del cuadro inferior derecho de la Fig.2 muestra un componente en la frecuencia real y otro componente en alias . A medida que aumenta durante la animación, disminuye. El punto en el que son iguales es un eje de simetría llamado frecuencia de plegado , también conocida como frecuencia de Nyquist .
El aliasing es importante cuando se intenta reconstruir la forma de onda original a partir de sus muestras. La técnica de reconstrucción más común produce la frecuencia más pequeña, por lo que suele ser importante que sea el mínimo único. Una condición necesaria y suficiente para ello se denomina condición de Nyquist . El cuadro inferior izquierdo de la Fig.2 muestra el resultado típico de la reconstrucción de las muestras disponibles. Hasta que se supera la frecuencia de Nyquist, la reconstrucción coincide con la forma de onda real (cuadro superior izquierdo). Después de eso, es el alias de baja frecuencia del cuadro superior.
Las figuras a continuación ofrecen representaciones adicionales del aliasing, debido al muestreo. Un gráfico de amplitud vs frecuencia (no tiempo) para una sola sinusoide a una frecuencia de 0,6 f s y algunos de sus aliases a 0,4 f s , 1,4 f s y 1,6 f s se vería como los 4 puntos negros en la Fig.3. Las líneas rojas representan las trayectorias (loci) de los 4 puntos si tuviéramos que ajustar la frecuencia y la amplitud de la sinusoide a lo largo del segmento rojo sólido (entre f s /2 y f s ). Sin importar qué función elijamos para cambiar la amplitud vs frecuencia, el gráfico exhibirá simetría entre 0 y f s . El plegado se observa a menudo en la práctica al ver el espectro de frecuencia de muestras de valor real, como la Fig.4.

Las sinusoides complejas son formas de onda cuyas muestras son números complejos , y el concepto de frecuencia negativa es necesario para distinguirlas. En ese caso, las frecuencias de los alias están dadas por simplemente : f N ( f ) = f + N f s . Por lo tanto, a medida que f aumenta de 0 a f s , f −1 ( f ) también aumenta (de – f s a 0). En consecuencia, las sinusoides complejas no presentan plegamiento .
Cuando se cumple la condición f s /2 > f para el componente de frecuencia más alta de la señal original, entonces se cumple para todos los componentes de frecuencia, una condición llamada criterio de Nyquist . Esto se aproxima típicamente filtrando la señal original para atenuar los componentes de alta frecuencia antes de muestrearla. Estos componentes de alta frecuencia atenuados aún generan alias de baja frecuencia, pero generalmente a amplitudes lo suficientemente bajas como para que no causen problemas. Un filtro elegido en previsión de una determinada frecuencia de muestreo se llama filtro anti-aliasing .
La señal filtrada puede reconstruirse posteriormente mediante algoritmos de interpolación sin una distorsión adicional significativa. La mayoría de las señales muestreadas no se almacenan y reconstruyen simplemente, pero la fidelidad de una reconstrucción teórica (mediante la fórmula de interpolación de Whittaker-Shannon ) es una medida habitual de la eficacia del muestreo.
Históricamente, el término aliasing surgió de la ingeniería de radio debido a la acción de los receptores superheterodinos . Cuando el receptor cambia múltiples señales a frecuencias más bajas, de RF a IF mediante heterodinación , una señal no deseada, de una frecuencia de RF igualmente alejada de la frecuencia del oscilador local (LO) que la señal deseada, pero en el lado equivocado del LO, puede terminar en la misma frecuencia IF que la deseada. Si es lo suficientemente fuerte, puede interferir con la recepción de la señal deseada. Esta señal no deseada se conoce como imagen o alias de la señal deseada.
El primer uso escrito de los términos "alias" y "aliasing" en el procesamiento de señales parece ser en un memorando técnico inédito de Bell Laboratories de 1949 [4] escrito por John Tukey y Richard Hamming . Ese documento incluye un ejemplo de aliasing de frecuencia que data de 1922. El primer uso publicado del término "aliasing" en este contexto se debe a Blackman y Tukey en 1958. [5] En su prefacio a la reimpresión de Dover [6] de este documento, señalan que la idea del aliasing había sido ilustrada gráficamente por Stumpf [7] diez años antes.
El informe técnico de Bell de 1949 se refiere al aliasing como si fuera un concepto bien conocido, pero no ofrece una fuente para el término. Gwilym Jenkins y Maurice Priestley atribuyen a Tukey el mérito de haberlo introducido en este contexto, [8] aunque un concepto análogo de aliasing se había introducido unos años antes [9] en diseños factoriales fraccionarios . Si bien Tukey realizó un trabajo significativo en experimentos factoriales [10] y ciertamente era consciente del aliasing en diseños fraccionarios, [11] no se puede determinar si su uso de "aliasing" en el procesamiento de señales estuvo inspirado conscientemente por tales diseños.
El aliasing se produce siempre que el uso de elementos discretos para capturar o producir una señal continua provoca ambigüedad de frecuencia.
El aliasing espacial, en particular de frecuencia angular, puede ocurrir al reproducir un campo de luz o un campo de sonido con elementos discretos, como en las pantallas 3D o en la síntesis de sonido por campos de ondas . [12]
Este aliasing es visible en imágenes como carteles con impresión lenticular : si tienen baja resolución angular, entonces cuando uno se mueve junto a ellos, digamos de izquierda a derecha, la imagen 2D no cambia inicialmente (por lo que parece moverse a la izquierda), luego, cuando uno se mueve a la siguiente imagen angular, la imagen cambia repentinamente (por lo que salta a la derecha) - y la frecuencia y amplitud de este movimiento de lado a lado corresponde a la resolución angular de la imagen (y, para la frecuencia, la velocidad del movimiento lateral del espectador), que es el aliasing angular del campo de luz 4D.
La falta de paralaje en el movimiento del espectador en imágenes 2D y en películas 3D producidas por gafas estereoscópicas (en películas 3D el efecto se llama " guiñada ", ya que la imagen parece girar sobre su eje) puede verse de manera similar como una pérdida de resolución angular, ya que todas las frecuencias angulares se vuelven 0 (constante).
Los efectos cualitativos del aliasing se pueden escuchar en la siguiente demostración de audio. Se reproducen seis ondas de diente de sierra en sucesión, con las dos primeras ondas de diente de sierra con una frecuencia fundamental de 440 Hz (A4), las dos segundas con una frecuencia fundamental de 880 Hz (A5) y las dos finales con una frecuencia de 1760 Hz (A6). Las ondas de diente de sierra se alternan entre ondas de diente de sierra con banda limitada (sin aliasing) y ondas de diente de sierra con aliasing y la frecuencia de muestreo es de 22050 Hz. Las ondas de diente de sierra con banda limitada se sintetizan a partir de la serie de Fourier de la forma de onda de diente de sierra de modo que no haya armónicos por encima de la frecuencia de Nyquist .
La distorsión de alias en las frecuencias más bajas es cada vez más obvia con frecuencias fundamentales más altas, y mientras que el diente de sierra limitado en banda todavía es claro a 1760 Hz, el diente de sierra con alias se degrada y se vuelve áspero con un zumbido audible en frecuencias más bajas que la fundamental.
También puede producirse una forma de aliasing espacial en los conjuntos de antenas o de micrófonos utilizados para estimar la dirección de llegada de una señal de onda, como en la exploración geofísica mediante ondas sísmicas. Las ondas deben muestrearse con una densidad mayor a dos puntos por longitud de onda , o la dirección de llegada de la onda se vuelve ambigua. [13]