

En teoría musical , una coma es un intervalo muy pequeño , la diferencia resultante de afinar una nota de dos maneras diferentes. [1] Tradicionalmente, hay dos comas más comunes; la coma sintónica , "la diferencia entre una tercera mayor justa y cuatro quintas perfectas menos dos octavas", y la coma pitagórica , "la diferencia entre doce quintas y siete octavas". [2] La palabra coma utilizada sin calificación se refiere a la coma sintónica , [3] que se puede definir, por ejemplo, como la diferencia entre un fa ♯ afinado usando el sistema de afinación pitagórica basado en re , y otro fa ♯ afinado usando el sistema de afinación de media nota de coma negra basado en re . Los intervalos separados por la proporción 81:80 se consideran la misma nota porque la escala cromática occidental de 12 notas no distingue los intervalos pitagóricos de los intervalos de 5 límites en su notación. Otros intervalos se consideran comas debido a las equivalencias enarmónicas de un sistema de afinación. Por ejemplo, en 53TET , B![]() ♭ y A ♯ se aproximan entre sí por el mismo intervalo, aunque están separados por un kleisma septimal .
♭ y A ♯ se aproximan entre sí por el mismo intervalo, aunque están separados por un kleisma septimal .
Traducido en este contexto, "coma" significa "un pelo", como en "cortado por un pelo" [ cita requerida ] . La palabra "coma" proviene del latín griego κόμμα , del antiguo * κοπ-μα : "el resultado o efecto de cortar". Una etimología más completa se da en el artículo κόμμα (griego antiguo) en el Wikcionario .
Dentro del mismo sistema de afinación, dos notas enarmónicamente equivalentes (como G ♯ y A ♭ ) pueden tener una frecuencia ligeramente diferente, y el intervalo entre ellas es una coma. Por ejemplo, en escalas extendidas producidas con afinación de cinco límites, un A ♭ afinado como una tercera mayor por debajo de C 5 y un G ♯ afinado como dos terceras mayores por encima de C 4 no son exactamente la misma nota, como lo serían en temperamento igual . El intervalo entre esas notas, la diesis , es una coma fácilmente audible (su tamaño es más del 40% de un semitono ).
Las comas se definen a menudo como la diferencia de tamaño entre dos semitonos. [ cita requerida ] Cada sistema de afinación de temperamento de mediotono produce una escala de 12 tonos caracterizada por dos tipos diferentes de semitonos (diatónico y cromático) y, por lo tanto, por una coma de tamaño único. Lo mismo ocurre con la afinación pitagórica.
En la entonación justa , se pueden producir más de dos tipos de semitonos. Por lo tanto, un único sistema de afinación puede caracterizarse por varias comas diferentes. Por ejemplo, una versión de uso común de la afinación de cinco límites produce una escala de 12 tonos con cuatro tipos de semitonos y cuatro comas .
El tamaño de las comas se expresa y compara comúnmente en términos de centavos : 1 ⁄ 1200 fracciones de una octava en una escala logarítmica .
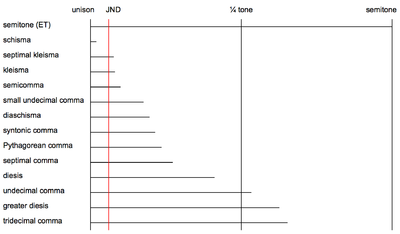
En la columna de abajo etiquetada como "Diferencia entre semitonos ", min 2 es el segundo menor (semitono diatónico), aug 1 es el unísono aumentado (semitono cromático), y S 1 , S 2 , S 3 , S 4 son semitonos como se definen aquí . En las columnas etiquetadas como " Intervalo 1" e "Intervalo 2", se supone que todos los intervalos están afinados en entonación justa . Observe que la coma pitagórica ( κ 𝜋 ) y la coma sintónica ( κ S ) son intervalos básicos que se pueden usar como criterios para definir algunas de las otras comas. Por ejemplo, la diferencia entre ellas es una pequeña coma llamada schisma . Un schisma no es audible en muchos contextos, ya que su tamaño es más estrecho que la diferencia audible más pequeña entre tonos (que es alrededor de seis centésimas, también conocida como diferencia apenas perceptible o JND).
Los microtonalistas han enumerado y nombrado muchas otras comas. [7]
La coma sintónica tiene un papel crucial en la historia de la música. Es la cantidad en la que algunas de las notas producidas en la afinación pitagórica se achataron o agudizaron para producir solo terceras menores y mayores. En la afinación pitagórica, los únicos intervalos altamente consonantes eran la quinta perfecta y su inversión, la cuarta perfecta . La tercera mayor pitagórica (81:64) y la tercera menor (32:27) eran disonantes , y esto impedía a los músicos usar libremente tríadas y acordes , lo que los obligaba a escribir música con una textura relativamente simple . Los músicos de finales de la Edad Media reconocieron que al templar ligeramente el tono de algunas notas, las terceras pitagóricas podían volverse consonantes . Por ejemplo, si disminuye la frecuencia de E por una coma sintónica (81:80), C–E (una tercera mayor) y E–G (una tercera menor) se vuelven simplemente: C–E se achata a una proporción justa de
y al mismo tiempo E–G se agudiza hasta la proporción justa de
Esto dio lugar a la creación de un nuevo sistema de afinación , conocido como temperamento de coma media , que permitió el pleno desarrollo de músicas de textura compleja , como la música polifónica , o melodías con acompañamiento instrumental . Desde entonces se desarrollaron otros sistemas de afinación, y la coma sintónica pasó a emplearse como valor de referencia para templar las quintas justas en toda la familia de temperamentos sintónicos , incluidos los temperamentos de coma media .
En el temperamento meantone de cuarto de coma , y en cualquier tipo de sistema de afinación de temperamento meantone que templa la quinta a un tamaño menor a 700 centésimas, la coma es una segunda disminuida , que se puede definir de manera equivalente como la diferencia entre:
En la afinación pitagórica y cualquier tipo de sistema de afinación de temperamento medio que templa la quinta a un tamaño mayor a 700 centésimas (como 1 /12 coma mediatono), la coma es lo opuesto a una segunda disminuida y, por lo tanto, lo opuesto a las diferencias enumeradas anteriormente. Más exactamente, en estos sistemas de afinación, la segunda disminuida es un intervalo descendente, mientras que la coma es su opuesto ascendente. Por ejemplo, la coma pitagórica (531441:524288, o aproximadamente 23,5 cents) se puede calcular como la diferencia entre un semitono cromático y uno diatónico, que es lo opuesto a una segunda disminuida pitagórica (524288:531441, o aproximadamente −23,5 cents).
En cada uno de los sistemas de afinación mencionados anteriormente, las diferencias mencionadas anteriormente tienen todas el mismo tamaño. Por ejemplo, en la afinación pitagórica todas son iguales al opuesto de una coma pitagórica , y en la afinación de cuarto de coma todas son iguales a una diesis .
En los años 2000-2004, Marc Sabat y Wolfgang von Schweinitz trabajaron juntos en Berlín para desarrollar un método para indicar con exactitud las notas en la notación de pentagrama. Este método se denominó notación de notas Helmholtz-Ellis JI extendida. [8] Sabat y Schweinitz toman los bemoles, los naturales y los sostenidos "convencionales" como una serie pitagórica de quintas perfectas. Por lo tanto, una serie de quintas perfectas que comienza con F procede CGDAEBF ♯ y así sucesivamente. La ventaja para los músicos es que la lectura convencional de las cuartas y quintas básicas sigue siendo familiar. Este enfoque también ha sido defendido por Daniel James Wolf y por Joe Monzo, que se refiere a él con el acrónimo HEWM (Helmholtz-Ellis-Wolf-Monzo). [9] En el diseño Sabat-Schweinitz, las comas sintónicas se marcan con flechas unidas al signo bemol, natural o sostenido, las comas séptimales con el símbolo de Giuseppe Tartini y los cuartos de tono indeciso con los signos de cuarto de tono de práctica común (una cruz simple y bemol invertido ). Para los primos más altos, se han diseñado signos adicionales. Para facilitar la estimación rápida de las alturas, se pueden agregar indicaciones de cents (desviaciones hacia abajo por debajo y desviaciones hacia arriba por encima de la alteración respectiva). La convención utilizada es que los cents escritos se refieren a la altura temperada implicada por el signo bemol, natural o sostenido y el nombre de la nota. Una de las grandes ventajas de cualquier notación de este tipo es que permite que la serie armónica natural se anote con precisión. Una leyenda completa y las fuentes para la notación (ver ejemplos) son de código abierto y están disponibles en Plainsound Music Edition. [ cita completa necesaria ] Por lo tanto, una escala pitagórica es CDEFGABC , mientras que una escala justa es CDE![]() FGA
FGA![]() B
B![]() C .
C .
El compositor Ben Johnston utiliza un "−" como alteración accidental para indicar que una nota se baja (una coma sintónica) o un "+" para indicar que una nota se eleva (una coma sintónica); [10] sin embargo, la "escala básica" de Johnston (los nominales simples ABCDEFG ) está afinada a la entonación justa y, por lo tanto, ya incluye la coma sintónica. Por lo tanto, una escala pitagórica es CD E+ FG A+ B+ C , mientras que una escala justa es CDEFGAB .
Las comas se utilizan con frecuencia en la descripción de temperamentos musicales , donde describen distinciones entre intervalos musicales que se eliminan mediante ese sistema de afinación. Una coma puede verse como la distancia entre dos intervalos musicales. Cuando se atenúa una coma determinada en un sistema de afinación, se elimina la capacidad de distinguir entre esos dos intervalos en esa afinación. Por ejemplo, la diferencia entre el semitono diatónico y el semitono cromático se llama diesis. El temperamento igual de 12 tonos, ampliamente utilizado, atenúa la diesis y, por lo tanto, no distingue entre los dos tipos diferentes de semitonos. Por otro lado, el temperamento igual de 19 tonos no atenúa esta coma y, por lo tanto, distingue entre los dos semitonos.
Ejemplos:
La siguiente tabla muestra la cantidad de pasos utilizados que corresponden a varios intervalos de igual temperamento en varios sistemas de afinación. Los ceros indican que el intervalo es una coma (es decir, está atenuado) en ese temperamento igual en particular. [ Aclaración necesaria ] Todas las relaciones de frecuencia en la primera columna están vinculadas a su artículo de Wikipedia.
La coma también puede considerarse como el intervalo fraccionario que queda después de un "círculo completo" de algún intervalo elegido repetido; los intervalos repetidos son todos del mismo tamaño, en tono relativo, y todos los tonos producidos se reducen o aumentan en octavas enteras hasta la octava que rodea el tono inicial. La coma pitagórica, por ejemplo, es la diferencia obtenida, digamos, entre A ♭ y G ♯ después de un círculo de doce quintas justas. Un círculo de tres terceras mayores justas, como A ♭ CEG ♯ , produce la diésis pequeña 128 /125 (41,1 cent ) entre G ♯ y A ♭ . Un círculo de cuatro terceras menores, como G ♯ BDFA ♭ , produce un intervalo de 648 /625 entre A ♭ y G ♯ , etc. Una propiedad interesante de los temperamentos es que esta diferencia permanece cualquiera que sea la afinación de los intervalos que forman el círculo. [11] En este sentido, las comas e intervalos de minutos similares nunca pueden templarse completamente, cualquiera que sea la afinación.
Una secuencia de comas define un temperamento musical a través de una secuencia única de comas en límites primos crecientes . [12] La primera coma de la secuencia de comas está en el q -límite, donde q es el n -ésimo primo impar (el primo 2 se ignora porque representa la octava) y n es el número de generadores . Las comas subsiguientes están en límites primos, cada una es el siguiente primo en secuencia por encima del último.
También existen varios intervalos llamados comas, que técnicamente no son comas porque no son fracciones racionales como las anteriores, sino que son aproximaciones irracionales de ellas. Entre ellas se encuentran las comas de Holdrian y Mercator [13], y el tamaño del paso de tono a tono en 53 TET .