Línea de Newton-Gauss

En geometría , la línea de Newton-Gauss (o línea de Gauss-Newton ) es la línea que une los puntos medios de las tres diagonales de un cuadrilátero completo .

Los puntos medios de las dos diagonales de un cuadrilátero convexo con dos lados paralelos como máximo son distintos y, por lo tanto, determinan una línea, la línea de Newton . Si los lados de dicho cuadrilátero se prolongan para formar un cuadrilátero completo, las diagonales del cuadrilátero siguen siendo diagonales del cuadrilátero completo y la línea de Newton del cuadrilátero es la línea de Newton-Gauss del cuadrilátero completo.

Cuadriláteros completos

Cuatro líneas cualesquiera en posición general (no hay dos líneas paralelas ni tres concurrentes) forman un cuadrilátero completo . Esta configuración consta de un total de seis puntos, los puntos de intersección de las cuatro líneas, con tres puntos en cada línea y exactamente dos líneas a través de cada punto. ^[1] Estos seis puntos se pueden dividir en pares de modo que los segmentos de línea determinados por cualquier par no intersequen ninguna de las cuatro líneas dadas excepto en los puntos finales. Estos tres segmentos de línea se denominan diagonales del cuadrilátero completo.

Existencia de la línea Newton−Gauss

Es un teorema bien conocido que los tres puntos medios de las diagonales de un cuadrilátero completo son colineales . ^[2] Hay varias demostraciones del resultado basadas en áreas ^[2] o productos de cuña ^[3] o, como la siguiente demostración, en el teorema de Menelao , debido a Hillyer y publicado en 1920. ^[4]

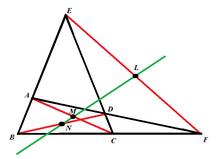
Sea el cuadrilátero completo $ABCA'B'C'$ etiquetado como en el diagrama con diagonales $AA', BB', CC'$ y sus respectivos puntos medios $L, M, N$ . Sean los puntos medios de $BC, CA', A'B$ $P, Q, R$ respectivamente. Usando triángulos similares se ve que $QR$ interseca $a AA'$ en $L$ , $RP$ interseca $a BB'$ en $M$ y $PQ$ interseca $a CC'$ en $N$ . Nuevamente, los triángulos similares proporcionan las siguientes proporciones,

{\frac {\overline {RL}}{\overline {LQ}}}={\frac {\overline {BA}}{\overline {AC}}},\quad {\frac {\overline { QN}}{\overline {NP}}}={\frac {\overline {A'C'}}{\overline {C'B}}},\quad {\frac {\overline {PM}}{\ overline {MR}}}={\frac {\overline {CB'}}{\overline {B'A'}}}.

Sin embargo, la línea $A'B'C$ interseca los lados del triángulo $△ ABC$ , por lo que, según el teorema de Menelao, el producto de los términos de los lados derechos es −1. Por lo tanto, el producto de los términos de los lados izquierdos también es −1 y, nuevamente, según el teorema de Menelao, los puntos $L, M, N$ son colineales en los lados del triángulo $△ PQR$ .

Aplicaciones a cuadriláteros cíclicos

Los siguientes son algunos resultados que utilizan la línea de Newton-Gauss de cuadriláteros completos que están asociados con cuadriláteros cíclicos , basados en el trabajo de Barbu y Patrascu. ^[5]

Ángulos iguales

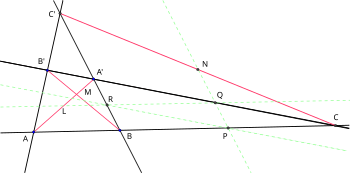
Dado cualquier cuadrilátero cíclico $ABCD$ , sea $F$ el punto de intersección entre las dos diagonales $AC$ y $BD$ . Prolonga las diagonales $AB$ y $CD$ hasta que se encuentren en el punto de intersección, $E$ . Sea N $el$ punto medio del segmento $EF$ y M el punto medio del segmento $BC$ $($ Figura 1).

Teorema

Si el punto medio del segmento de recta $BF$ es $P$ , la recta de Newton-Gauss del cuadrilátero completo $ABCDEF$ y la recta $PM$ determinan un ángulo $∠ PMN$ igual a $∠ EFD$ .

Prueba

Primero demuestre que los triángulos $△ NPM, △ EDF$ son semejantes .

Como $BE ∥ PN$ y $FC ∥ PM$ , sabemos $que ∠ NPM = ∠ EAC$ . Además, ${\tfrac {\overline {BE}}{\overline {PN}}}={\tfrac {\overline {FC}}{\overline {PM}}}=2.$

En el cuadrilátero cíclico $ABCD$ , se cumplen estas igualdades :

{\begin{aligned}\ángulo EDF&=\ángulo ADF+\ángulo EDA,\\&=\ángulo ACB+\ángulo ABC,\\&=\ángulo EAC.\end{aligned}}

Por lo tanto, $∠ NPM = ∠ EDF$ .

Sean $R 1, R 2$ los radios de las circunferencias circunscritas de $△ EDB, △ FCD$ respectivamente. Aplicando la ley de senos a los triángulos, se obtiene:

{\frac {\overline {BE}}{\overline {FC}}}={\frac {2R_{1}\sin \ángulo EDB}{2R_{2}\sin \ángulo FDC}}={\frac {R_{1}}{R_{2}}}={\frac {2R_{1}\sin \ángulo EBD}{2R_{2}\sin \ángulo FCD}}={\frac {\overline {DE}}{\overline {DF}}}.

Como $BE = 2 \cdot PN$ y $FC = 2 \cdot PM$ , esto demuestra la igualdad. Se deduce la similitud de los triángulos $△$ $PMN$ $, △$ $DFE$ y $∠$ $NMP$ $= ∠$ $EFD$ . ${\tfrac {\overline {PN}}{\overline {PM}}}={\tfrac {\overline {DE}}{\overline {DF}}}.$

Observación

Si $Q$ es el punto medio del segmento de recta $FC$ , se deduce por el mismo razonamiento que $∠ NMQ = ∠ EFA$ .

Líneas isogonales

Teorema

La línea que pasa por $E$ paralela a la línea de Newton-Gauss del cuadrilátero completo $ABCDEF$ y la línea $EF$ son líneas isogonales de $∠ BEC$ , es decir, cada línea es una reflexión de la otra alrededor de la bisectriz del ángulo . ^[5] (Figura 2)

Prueba

Los triángulos $△ EDF, △ NPM$ son similares según el argumento anterior, por lo que $∠ DEF = ∠ PNM$ . Sea $E'$ el punto de intersección de $BC$ y la línea paralela a la línea de Newton-Gauss $NM$ que pasa por $E$ .

Como $PN ∥ BE$ y $NM ∥ EE',$ $∠ BEF = ∠ PNF$ y $∠ FNM = ∠ E'EF$ .

Por lo tanto,

{\begin{aligned}\ángulo CEE'&=\ángulo DEF-\ángulo E'EF,\\&=\ángulo PNM-\ángulo FNM,\\&=\ángulo PNF=\ángulo BEF.\end{aligned}}

Dos cuadriláteros cíclicos que comparten una línea de Newton-Gauss

Lema

Sean $G$ y $H$ las proyecciones ortogonales del punto $F$ sobre las rectas $AB$ y $CD$ respectivamente.

Los cuadriláteros $MPGN$ y $MQHN$ son cuadriláteros cíclicos. ^[5]

Prueba

$∠ EFD = ∠ PMN$ , como se mostró anteriormente. Los puntos $P$ y $N$ son los circuncentros respectivos de los triángulos rectángulos $△ BFG, △ EFG$ . Por lo tanto, $∠ PGF = ∠ PFG$ y $∠ FGN = ∠ GFN$ .

Por lo tanto,

{\begin{aligned}\ángulo PGN+\ángulo PMN&=(\ángulo PGF+\ángulo FGN)+\ángulo PMN\\[4pt]&=\ángulo PFG+\ángulo GFN+\ángulo EFD\\[4pt]&=180^{\circ }\end{aligned}}.

Por lo tanto, $MPGN$ es un cuadrilátero cíclico y, por el mismo razonamiento, $MQHN$ también se encuentra en un círculo.

Teorema

Extienda las líneas $GF, HF$ para intersecar $EC, EB$ en $I, J$ respectivamente (Figura 4).

Los cuadriláteros completos $EFGHIJ$ y $ABCDEF$ tienen la misma línea de Newton-Gauss. ^[5]

Prueba

Los dos cuadriláteros completos comparten una diagonal, $EF$ . $N$ se encuentra en la línea de Newton-Gauss de ambos cuadriláteros. $N$ es equidistante de $G$ y $H$ , ya que es el circuncentro del cuadrilátero cíclico $EGFH$ .

Si los triángulos $△ GMP, △ HMQ$ son congruentes , se deduce que $M$ se encuentra en la bisectriz perpendicular de la línea $HG$ . Por lo tanto, la línea $MN$ contiene el punto medio de $GH$ , y es la línea de Newton-Gauss de $EFGHIJ$ .

Para demostrar que los triángulos $△ GMP, △ HMQ$ son congruentes, primero observe que $PMQF$ es un paralelogramo , ya que los puntos $M, P$ son puntos medios de $BF, BC$ respectivamente.

Por lo tanto,

{\begin{aligned}&{\overline {MP}}={\overline {QF}}={\overline {HQ}},\\&{\overline {GP}}={\overline {PF}}={\overline {MQ}},\\&\angle MPF=\angle FQM.\end{aligned}}

Tenga en cuenta también que

\ángulo FPG=2\ángulo PBG=2\ángulo DBA=2\ángulo DCA=2\ángulo HCF=\ángulo HQF.

Por eso,

{\begin{aligned}\ángulo MPG&=\ángulo MPF+\ángulo FPG,\\&=\ángulo FQM+\ángulo HQF,\\&=\ángulo HQF+\ángulo FQM,\\&=\ángulo HQM.\end{aligned}}

Por lo tanto, $△ GMP$ y $△ HMQ$ son congruentes según SAS.

Observación

Debido a que $△ GMP y △ HMQ$ son triángulos congruentes, sus circunferencias circunscritas $MPGN y MQHN$ también son congruentes .

= Relación con el punto Miquel

El punto en el infinito a lo largo de la línea de Newton es el conjugado isogonal del punto de Miquel.

Historia

La prueba de la línea de Newton-Gauss fue desarrollada por los dos matemáticos que le dan nombre: Sir Isaac Newton y Carl Friedrich Gauss . ^{[ cita requerida ]} El marco inicial para este teorema proviene del trabajo de Newton , en su teorema anterior sobre la línea de Newton , en el que Newton demostró que el centro de una cónica inscrita en un cuadrilátero se encuentra en la línea de Newton-Gauss. ^[6]

El teorema de Gauss y Bodenmiller establece que los tres círculos cuyos diámetros son las diagonales de un cuadrilátero completo son coaxiales . ^[7]

Notas

^ Alperin, Roger C. (6 de enero de 2012). "Líneas de Gauss-Newton y cónicas de once puntos". Research Gate .
^ por Johnson 2007, pág. 62
^ Pedoe, Dan (1988) [1970], Geometría: un curso completo , Dover, págs. 46-47, ISBN 0-486-65812-0
^ Johnson 2007, pág. 152
^ abcd Patrascu, Ion. "Algunas propiedades de la línea Newton-Gauss" (PDF) . Forum Geometricorum . Consultado el 29 de abril de 2019 .
^ Wells, David (1991), Diccionario Penguin de geometría curiosa e interesante, Penguin Books, pág. 36, ISBN 978-0-14-011813-1
^ Johnson 2007, pág. 172

Referencias

Johnson, Roger A. (2007) [1929], Geometría euclidiana avanzada , Dover, ISBN 978-0-486-46237-0
- (disponible en línea como) Johnson, Roger A. (1929). "Geometría moderna: un tratado elemental sobre la geometría del triángulo y el círculo". HathiTrust . Consultado el 28 de mayo de 2019 .

Enlaces externos

Bogomonly, Alexander. "Teorema del cuadrilátero completo: ¿qué es?" . Consultado el 11 de mayo de 2019 .