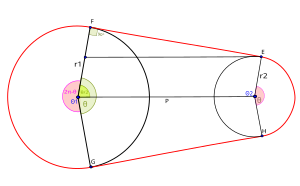
El problema del cinturón El problema de la correa es un problema matemático que requiere encontrar la longitud de una correa cruzada que conecta dos poleas circulares con radios r 1 y r 2 cuyos centros están separados por una distancia P . La solución del problema de la correa requiere trigonometría y los conceptos de línea bitangente , ángulo vertical y ángulos congruentes .
Solución Claramente los triángulos ACO y ADO son triángulos rectángulos congruentes , al igual que los triángulos BEO y BFO. Además, los triángulos ACO y BEO son semejantes . Por lo tanto , los ángulos CAO, DAO, EBO y FBO son todos iguales. Denotando este ángulo por (denominado en radianes ), la longitud de la correa es φ {\estilo de visualización \varphi}
do Oh + D Oh + mi Oh + F Oh + arco do D + arco mi F {\displaystyle CO+DO+EO+FO+{\text{arco}}CD+{\text{arco}}EF\,\!} = 2 a 1 broncearse ( φ ) + 2 a 2 broncearse ( φ ) + ( 2 π − 2 φ ) a 1 + ( 2 π − 2 φ ) a 2 {\displaystyle =2r_{1}\tan(\varphi )+2r_{2}\tan(\varphi )+(2\pi -2\varphi )r_{1}+(2\pi -2\varphi )r_ {2}\,\!} = 2 ( a 1 + a 2 ) ( broncearse ( φ ) + π − φ ) {\displaystyle =2(r_{1}+r_{2})(\tan(\varphi )+\pi -\varphi )\,\!} Esto explota la conveniencia de denominar ángulos en radianes: la longitud de un arco = el radio × la medida del ángulo que mira hacia el arco .
Para encontrar vemos por la semejanza de los triángulos ACO y BEO que φ {\estilo de visualización \varphi}
A Oh B Oh = A do B mi {\displaystyle {\frac {AO}{BO}}={\frac {AC}{BE}}\,\!} ⇒ PAG − incógnita incógnita = a 1 a 2 {\displaystyle \Rightarrow {\frac {Px}{x}}={\frac {r_{1}}{r_{2}}}\,\!} ⇒ PAG incógnita = a 1 + a 2 a 2 {\displaystyle \Rightarrow {\frac {P}{x}}={\frac {r_{1}+r_{2}}{r_{2}}}\,\!} ⇒ incógnita = PAG a 2 a 1 + a 2 {\displaystyle \Rightarrow {x}={\frac {Pr_{2}}{r_{1}+r_{2}}}\,\!}
porque ( φ ) = a 2 incógnita = a 2 ( PAG a 2 a 1 + a 2 ) = a 1 + a 2 PAG {\displaystyle \cos(\varphi )={\frac {r_{2}}{x}}={\frac {r_{2}}{\left({\dfrac {Pr_{2}}{r_{1}+r_{2}}}\right)}}={\frac {r_{1}+r_{2}}{P}}\,\!} ⇒ φ = arcos ( a 1 + a 2 PAG ) {\displaystyle \Rightarrow \varphi =\arccos \left({\frac {r_{1}+r_{2}}{P}}\right)\,\!} Para P fijo , la longitud de la correa depende solo de la suma de los valores de radio r 1 + r 2 , y no de sus valores individuales.
Problema de polea El problema de la polea Existen otros tipos de problemas similares al problema de la correa. El problema de la polea , como se muestra, es similar al problema de la correa; sin embargo, la correa no se cruza a sí misma. En el problema de la polea, la longitud de la correa es
2 PAG pecado ( θ 2 ) + a 1 ( 2 π − θ ) + a 2 θ , {\displaystyle 2P\sin \left({\frac {\theta }{2}}\right)+r_{1}(2\pi -\theta )+r_{2}{\theta }\,,} donde r 1 representa el radio de la polea más grande, r 2 representa el radio de la más pequeña y:
θ = 2 arcos ( a 1 − a 2 PAG ) . {\displaystyle \theta =2\arccos \left({\frac {r_{1}-r_{2}}{P}}\right)\,.}
Aplicaciones El problema de la correa se utiliza [1] en el diseño de aviones , engranajes de bicicletas , automóviles y otros elementos con poleas o correas que se cruzan entre sí. El problema de la polea también se utiliza en el diseño de cintas transportadoras que se encuentran en las cintas transportadoras de equipaje de los aeropuertos y en las líneas de fabricación automatizadas . [2]
Véase también
Referencias ^ Ejemplos de trigonometría en la vida real Archivado el 25 de abril de 2009 en Wayback Machine . ^ Trigonometría utilizada en cintas transportadoras Archivado el 22 de febrero de 2012 en Wayback Machine .