Función de transferencia óptica

Función que especifica cómo se capturan diferentes frecuencias espaciales mediante un sistema óptico

Ilustración de la función de transferencia óptica (OTF) y su relación con la calidad de la imagen. Función de transferencia óptica de un sistema de imágenes ópticas bien enfocado (a) y desenfocado sin aberraciones (d). Como la función de transferencia óptica de estos sistemas es real y no negativa, la función de transferencia óptica es por definición igual a la función de transferencia de modulación (MTF). Las imágenes de una fuente puntual y un objetivo radial con alta frecuencia espacial se muestran en (b, e) y (c, f), respectivamente. Nótese que la escala de las imágenes de la fuente puntual (b, e) es cuatro veces menor que la de las imágenes del objetivo radial.

La función de transferencia óptica ( OTF ) de un sistema óptico como una cámara , un microscopio , un ojo humano o un proyector especifica cómo se capturan o transmiten las diferentes frecuencias espaciales. Los ingenieros ópticos la utilizan para describir cómo la óptica proyecta la luz del objeto o la escena sobre una película fotográfica, un conjunto de detectores , una retina , una pantalla o simplemente el siguiente elemento de la cadena de transmisión óptica. Una variante, la función de transferencia de modulación ( MTF ), ignora los efectos de fase, pero es equivalente a la OTF en muchas situaciones.

Cada función de transferencia especifica la respuesta a un patrón periódico de ondas sinusoidales que pasa a través del sistema de lentes, como una función de su frecuencia espacial o período, y su orientación. Formalmente, la OTF se define como la transformada de Fourier de la función de dispersión de puntos (PSF, es decir, la respuesta al impulso de la óptica, la imagen de una fuente puntual). Como transformada de Fourier, la OTF tiene un valor complejo; pero tendrá un valor real en el caso común de una PSF que sea simétrica respecto de su centro. La MTF se define formalmente como la magnitud (valor absoluto) de la OTF compleja.

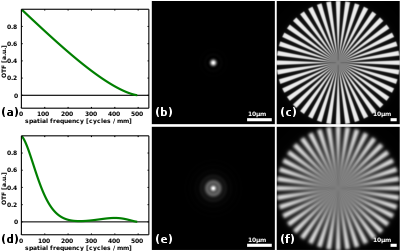
La imagen de la derecha muestra las funciones de transferencia óptica para dos sistemas ópticos diferentes en los paneles (a) y (d). El primero corresponde al sistema de formación de imágenes ideal, limitado por difracción , con una pupila circular . Su función de transferencia disminuye aproximadamente de forma gradual con la frecuencia espacial hasta que alcanza el límite de difracción, en este caso a 500 ciclos por milímetro o un período de 2 μm. Dado que este sistema de formación de imágenes captura características periódicas tan pequeñas como este período, podría decirse que su resolución es de 2 μm. ^[1] El panel (d) muestra un sistema óptico que está desenfocado. Esto conduce a una reducción marcada del contraste en comparación con el sistema de formación de imágenes limitado por difracción. Se puede ver que el contraste es cero alrededor de 250 ciclos/mm, o períodos de 4 μm. Esto explica por qué las imágenes del sistema desenfocado (e,f) son más borrosas que las del sistema limitado por difracción (b,c). Obsérvese que, si bien el sistema desenfocado tiene un contraste muy bajo en frecuencias espaciales de alrededor de 250 ciclos/mm, el contraste en frecuencias espaciales cercanas al límite de difracción de 500 ciclos/mm está limitado por la difracción. Una observación minuciosa de la imagen del panel (f) muestra que la imagen de las grandes densidades de radios cerca del centro del objetivo de radios es relativamente nítida.

Definición y conceptos relacionados

Dado que la función de transferencia óptica ^[2] (OTF) se define como la transformada de Fourier de la función de dispersión puntual (PSF), en términos generales es una función de frecuencia espacial de valor complejo . La proyección de un patrón periódico específico se representa mediante un número complejo con valor absoluto y argumento complejo proporcional al contraste relativo y la traslación de la proyección proyectada, respectivamente.

Varias caracterizaciones estrechamente relacionadas de un sistema óptico que presenta coma, una aberración típica que ocurre fuera del eje. (a) La función de dispersión puntual (PSF) es la imagen de una fuente puntual. (b) La imagen de una línea se denomina función de dispersión lineal, en este caso una línea vertical. La función de dispersión lineal es directamente proporcional a la integración vertical de la imagen de dispersión puntual. La función de transferencia óptica (OTF) se define como la transformada de Fourier de la función de dispersión puntual y, por lo tanto, generalmente es una función compleja bidimensional. Por lo general, solo se muestra un corte unidimensional (c), que corresponde a la transformada de Fourier de la función de dispersión lineal. La línea verde gruesa indica la parte real de la función y la línea roja delgada la parte imaginaria. A menudo, solo se muestra el valor absoluto de la función compleja, lo que permite la visualización de la función bidimensional (d); sin embargo, lo más común es que solo se muestre la función unidimensional (e). Esta última generalmente se normaliza en la frecuencia espacial cero y se la denomina función de transferencia de modulación (MTF). Para completar, el argumento complejo a veces se proporciona como la función de transferencia de fase (PhTF), que se muestra en el panel (f).

A menudo, la reducción del contraste es de mayor interés y la traducción del patrón puede ignorarse. El contraste relativo viene dado por el valor absoluto de la función de transferencia óptica, una función comúnmente denominada función de transferencia de modulación ( MTF ). Sus valores indican cuánto del contraste del objeto se captura en la imagen como una función de la frecuencia espacial. La MTF tiende a disminuir con el aumento de la frecuencia espacial de 1 a 0 (en el límite de difracción); sin embargo, la función a menudo no es monótona . Por otro lado, cuando también es importante la traducción del patrón, el argumento complejo de la función de transferencia óptica puede representarse como una segunda función de valor real, comúnmente denominada función de transferencia de fase ( PhTF ). La función de transferencia óptica de valor complejo puede verse como una combinación de estas dos funciones de valor real:

${\displaystyle \mathrm {OTF} (\nu )=\mathrm {MTF} (\nu )e^{i\,\mathrm {PhTF} (\nu )}}$

dónde

${\displaystyle \mathrm {MTF} (\nu )=\left\vert \mathrm {OTF} (\nu )\right\vert ,}$

${\displaystyle \mathrm {PhTF} (\nu )=\mathrm {arg} (\mathrm {OTF} (\nu )),}$

y representa la función argumento compleja, mientras que es la frecuencia espacial del patrón periódico. En general es un vector con una frecuencia espacial para cada dimensión, es decir, indica también la dirección del patrón periódico. ${\displaystyle \mathrm {arg} (\cdot )}$ ${\displaystyle \nu }$ ${\displaystyle \nu }$

La respuesta al impulso de un sistema óptico bien enfocado es una distribución de intensidad tridimensional con un máximo en el plano focal y, por lo tanto, se puede medir registrando una pila de imágenes mientras se desplaza el detector axialmente. En consecuencia, la función de transferencia óptica tridimensional se puede definir como la transformada de Fourier tridimensional de la respuesta al impulso. Aunque normalmente solo se utiliza una sección unidimensional o, a veces, bidimensional, la función de transferencia óptica tridimensional puede mejorar la comprensión de los microscopios, como el microscopio de iluminación estructurada.

Fiel a la definición de función de transferencia , debería indicar la fracción de luz que se detectó desde el objeto de fuente puntual. Sin embargo, normalmente el contraste relativo a la cantidad total de luz detectada es lo más importante. Por lo tanto, es una práctica común normalizar la función de transferencia óptica a la intensidad detectada, por lo tanto , . ${\displaystyle \mathrm {OTF} (0)=\mathrm {MTF} (0)}$ ${\displaystyle \mathrm {MTF} (0)\equiv 1}$

En general, la función de transferencia óptica depende de factores como el espectro y la polarización de la luz emitida y la posición de la fuente puntual. Por ejemplo, el contraste y la resolución de la imagen suelen ser óptimos en el centro de la imagen y se deterioran hacia los bordes del campo de visión. Cuando se produce una variación significativa, la función de transferencia óptica puede calcularse para un conjunto de posiciones o colores representativos.

A veces resulta más práctico definir las funciones de transferencia en función de un patrón binario de rayas blancas y negras. La función de transferencia para un patrón periódico de rayas blancas y negras de igual ancho se denomina función de transferencia de contraste (CTF) . ^[3]

Ejemplos

El OTF de un sistema de lentes ideal

Un sistema de lentes perfecto proporcionará una proyección de alto contraste sin cambiar el patrón periódico, por lo que la función de transferencia óptica es idéntica a la función de transferencia de modulación. Normalmente, el contraste se reducirá gradualmente hacia cero en un punto definido por la resolución de la óptica. Por ejemplo, un sistema de imágenes ópticas f/4 perfecto y sin aberraciones utilizado en la longitud de onda visible de 500 nm tendría la función de transferencia óptica que se muestra en la figura de la derecha.

Función de transferencia e imagen de ejemplo de un sistema de imágenes ideal, libre de aberraciones ópticas (limitado por difracción).

En el gráfico se puede leer que el contraste se reduce gradualmente y llega a cero en la frecuencia espacial de 500 ciclos por milímetro, en otras palabras, la resolución óptica de la proyección de la imagen es ^de 1/500 de milímetro, o 2 micrómetros. En consecuencia, para este dispositivo de imagen en particular, los radios se vuelven cada vez más borrosos hacia el centro hasta que se fusionan en un disco gris sin resolución. Tenga en cuenta que a veces la función de transferencia óptica se da en unidades del objeto o espacio muestral, ángulo de observación, ancho de película o normalizada al máximo teórico. La conversión entre los dos es típicamente una cuestión de multiplicación o división. Por ejemplo, un microscopio normalmente aumenta todo de 10 a 100 veces, y una cámara réflex generalmente reducirá el tamaño de los objetos a una distancia de 5 metros en un factor de 100 a 200.

La resolución de un dispositivo de imagen digital no solo está limitada por la óptica, sino también por el número de píxeles, más en particular por su distancia de separación. Como lo explica el teorema de muestreo de Nyquist-Shannon , para que coincida con la resolución óptica del ejemplo dado, los píxeles de cada canal de color deben estar separados por 1 micrómetro, la mitad del período de 500 ciclos por milímetro. Un mayor número de píxeles en el mismo tamaño de sensor no permitirá la resolución de detalles más finos. Por otro lado, cuando el espaciado de píxeles es mayor de 1 micrómetro, la resolución estará limitada por la separación entre píxeles; además, el aliasing puede conducir a una reducción adicional de la fidelidad de la imagen.

OTF de un sistema de lentes imperfecto

Un sistema de imágenes imperfecto y aberrado podría poseer la función de transferencia óptica que se muestra en la siguiente figura.

Función de transferencia e imagen de ejemplo de un sistema de imágenes ópticas f/4 a 500 nm con aberración esférica con coeficiente Zernike estándar de 0,25.

Como sistema de lentes ideal, el contraste llega a cero en la frecuencia espacial de 500 ciclos por milímetro. Sin embargo, a frecuencias espaciales más bajas, el contraste es considerablemente menor que el del sistema perfecto en el ejemplo anterior. De hecho, el contraste se vuelve cero en varias ocasiones incluso para frecuencias espaciales inferiores a 500 ciclos por milímetro. Esto explica las bandas circulares grises en la imagen de los radios que se muestra en la figura anterior. Entre las bandas grises, los radios parecen invertirse de negro a blanco y viceversa ; esto se conoce como inversión de contraste, directamente relacionada con la inversión de signo en la parte real de la función de transferencia óptica, y se representa como un desplazamiento de medio período para algunos patrones periódicos.

Aunque se podría argumentar que la resolución tanto del sistema ideal como del imperfecto es de 2 μm, o 500 LP/mm, es evidente que las imágenes del último ejemplo son menos nítidas. Una definición de resolución más acorde con la calidad percibida utilizaría en cambio la frecuencia espacial en la que se produce el primer cero, 10 μm, o 100 LP/mm. Las definiciones de resolución, incluso para sistemas de imágenes perfectos, varían ampliamente. La función de transferencia óptica proporciona una imagen más completa y unívoca.

La OTF de un sistema óptico con una aberración simétrica no rotacional

Cuando se observa a través de un sistema óptico con aberración de trébol, la imagen de un objeto puntual se verá como una estrella de tres puntas (a). Como la función de dispersión de puntos no es simétrica rotacionalmente, solo una función de transferencia óptica bidimensional puede describirla bien (b). La altura del gráfico de superficie indica el valor absoluto y el tono indica el argumento complejo de la función. La simulación en (c) muestra un objetivo radial fotografiado por un dispositivo de imágenes de este tipo.

Los sistemas ópticos, y en particular las aberraciones ópticas , no siempre son simétricos rotacionalmente. Por lo tanto, los patrones periódicos que tienen una orientación diferente se pueden representar con un contraste diferente incluso si su periodicidad es la misma. La función de transferencia óptica o las funciones de transferencia de modulación son, por lo tanto, funciones generalmente bidimensionales. Las siguientes figuras muestran el equivalente bidimensional del sistema ideal e imperfecto discutido anteriormente, para un sistema óptico con trébol , una aberración no simétrica rotacional.

Las funciones de transferencia óptica no siempre tienen valores reales. Los patrones de períodos pueden variar en cualquier cantidad, dependiendo de la aberración del sistema. Este es generalmente el caso de las aberraciones simétricas no rotacionales. El tono de los colores de los gráficos de superficie en la figura anterior indica la fase. Se puede ver que, mientras que para las aberraciones simétricas rotacionales la fase es 0 o π y, por lo tanto, la función de transferencia tiene un valor real, para la aberración simétrica no rotacional la función de transferencia tiene un componente imaginario y la fase varía continuamente.

Ejemplo práctico: sistema de vídeo de alta definición

Mientras que la resolución óptica , tal como se utiliza habitualmente en relación con los sistemas de cámaras, describe únicamente la cantidad de píxeles de una imagen y, por lo tanto, la capacidad de mostrar detalles finos, la función de transferencia describe la capacidad de los píxeles adyacentes de cambiar de negro a blanco en respuesta a patrones de frecuencia espacial variable y, por lo tanto, la capacidad real de mostrar detalles finos, ya sea con contraste total o reducido. Una imagen reproducida con una función de transferencia óptica que "se desvanece" a frecuencias espaciales altas aparecerá "borrosa" en el lenguaje cotidiano.

Tomando el ejemplo de un sistema de video de alta definición (HD) actual, con 1920 por 1080 píxeles, el teorema de Nyquist establece que debería ser posible, en un sistema perfecto, resolver completamente (con verdaderas transiciones de negro a blanco) un total de 1920 líneas alternas en blanco y negro combinadas, lo que también se conoce como una frecuencia espacial de 1920/2=960 pares de líneas por ancho de imagen, o 960 ciclos por ancho de imagen (también son posibles las definiciones en términos de ciclos por unidad de ángulo o por mm, pero generalmente menos claras cuando se trata de cámaras y más apropiadas para telescopios, etc.). En la práctica, esto está lejos de ser el caso, y las frecuencias espaciales que se acercan a la tasa de Nyquist generalmente se reproducirán con una amplitud decreciente, de modo que los detalles finos, aunque se pueden ver, se reducen en gran medida en contraste. Esto da lugar a la interesante observación de que, por ejemplo, una imagen de televisión de definición estándar derivada de un escáner de película que utiliza sobremuestreo , como se describe más adelante, puede aparecer más nítida que una imagen de alta definición tomada con una cámara con una función de transferencia de modulación deficiente. Las dos imágenes muestran una diferencia interesante que a menudo se pasa por alto: la primera tiene un contraste completo en los detalles hasta cierto punto, pero luego no presenta detalles realmente finos, mientras que la segunda contiene detalles más finos, pero con un contraste tan reducido que parece inferior en general.

La función de transferencia óptica tridimensional

Funciones de dispersión de puntos tridimensionales (a, c) y funciones de transferencia de modulación correspondientes (b, d) de un microscopio de campo amplio (a, b) y un microscopio confocal (c, d). En ambos casos, la apertura numérica del objetivo es 1,49 y el índice de refracción del medio 1,52. Se supone que la longitud de onda de la luz emitida es de 600 nm y, en el caso del microscopio confocal, la de la luz de excitación es de 500 nm con polarización circular. Se corta una sección para visualizar la distribución de intensidad interna. Los colores que se muestran en la escala de colores logarítmica indican la irradiancia (a, c) y la densidad espectral (b, d) normalizadas al valor máximo.

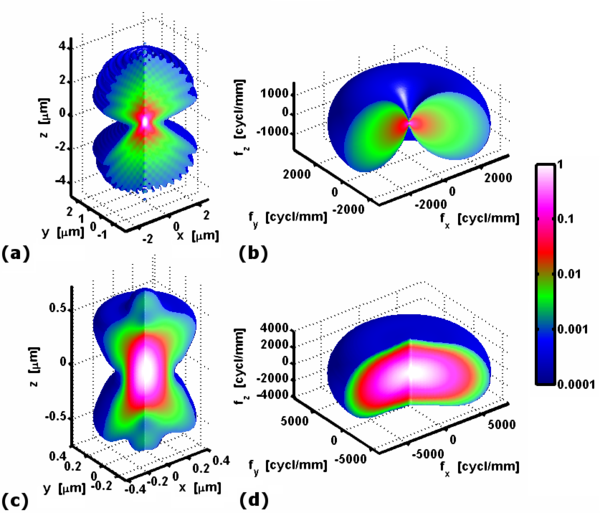
Aunque normalmente se piensa en una imagen como plana o bidimensional, el sistema de obtención de imágenes producirá una distribución de intensidad tridimensional en el espacio de la imagen que, en principio, se puede medir. Por ejemplo, un sensor bidimensional podría trasladarse para capturar una distribución de intensidad tridimensional. La imagen de una fuente puntual es también una distribución de intensidad tridimensional (3D) que se puede representar mediante una función de dispersión de puntos 3D. Como ejemplo, la figura de la derecha muestra la función de dispersión de puntos 3D en el espacio del objeto de un microscopio de campo amplio (a) junto con la de un microscopio confocal (c). Aunque se utiliza el mismo objetivo de microscopio con una apertura numérica de 1,49, está claro que la función de dispersión de puntos confocal es más compacta tanto en las dimensiones laterales (x, y) como en la dimensión axial (z). Se podría concluir correctamente que la resolución de un microscopio confocal es superior a la de un microscopio de campo amplio en las tres dimensiones.

Una función de transferencia óptica tridimensional se puede calcular como la transformada de Fourier tridimensional de la función de dispersión de puntos 3D. Su magnitud codificada por colores se representa gráficamente en los paneles (b) y (d), que corresponden a las funciones de dispersión de puntos que se muestran en los paneles (a) y (c), respectivamente. La función de transferencia del microscopio de campo amplio tiene un soporte que es la mitad del del microscopio confocal en las tres dimensiones, lo que confirma la resolución inferior del microscopio de campo amplio mencionada anteriormente. Nótese que a lo largo del eje z , para x  =  y  = 0, la función de transferencia es cero en todas partes excepto en el origen. Este cono faltante es un problema bien conocido que impide el seccionamiento óptico utilizando un microscopio de campo amplio. ^[4]

La función de transferencia óptica bidimensional en el plano focal se puede calcular mediante la integración de la función de transferencia óptica 3D a lo largo del eje z . Aunque la función de transferencia 3D del microscopio de campo amplio (b) es cero en el eje z para z  ≠ 0; su integral, la transferencia óptica 2D, alcanza un máximo en x  =  y  = 0. Esto solo es posible porque la función de transferencia óptica 3D diverge en el origen x  =  y  =  z  = 0. Los valores de la función a lo largo del eje z de la función de transferencia óptica 3D corresponden a la función delta de Dirac .

Cálculo

La mayoría de los programas de diseño óptico tienen la funcionalidad de calcular la función de transferencia óptica o de modulación de un diseño de lente. Los sistemas ideales como los de los ejemplos aquí presentados se calculan fácilmente de forma numérica utilizando programas como Julia , GNU Octave o Matlab y, en algunos casos específicos, incluso de forma analítica. La función de transferencia óptica se puede calcular siguiendo dos enfoques: ^[5]

1. como la transformada de Fourier de la función de dispersión de puntos incoherente , o
2. como la autocorrelación de la función pupilar del sistema óptico

Matemáticamente, ambos enfoques son equivalentes. Los cálculos numéricos suelen realizarse de forma más eficiente mediante la transformada de Fourier; sin embargo, el cálculo analítico puede resultar más práctico si se utiliza el enfoque de autocorrelación.

Ejemplo

Sistema de lentes ideal con apertura circular

Autocorrelación de la función pupilar

Dado que la función de transferencia óptica es la transformada de Fourier de la función de dispersión de puntos , y la función de dispersión de puntos es el cuadrado absoluto de la función pupila transformada de Fourier inversa , la función de transferencia óptica también se puede calcular directamente a partir de la función pupila . A partir del teorema de convolución se puede ver que la función de transferencia óptica es de hecho la autocorrelación de la función pupila . ^[5]

La función pupila de un sistema óptico ideal con una apertura circular es un disco de radio unitario. La función de transferencia óptica de un sistema de este tipo se puede calcular geométricamente a partir del área de intersección entre dos discos idénticos a una distancia de , donde es la frecuencia espacial normalizada a la frecuencia transmitida más alta. ^[2] En general, la función de transferencia óptica se normaliza a un valor máximo de uno para , por lo que el área resultante debe dividirse por . ${\displaystyle 2\nu }$ ${\displaystyle \nu }$ ${\displaystyle \nu =0}$ ${\displaystyle \pi }$

El área de intersección se puede calcular como la suma de las áreas de dos segmentos circulares idénticos : , donde es el ángulo del segmento circular. Sustituyendo , y utilizando las igualdades y , la ecuación para el área se puede reescribir como . Por lo tanto, la función de transferencia óptica normalizada viene dada por: ${\displaystyle \theta /2-\sin(\theta )/2}$ ${\displaystyle \theta }$ ${\displaystyle |\nu |=\cos(\theta /2)}$ ${\displaystyle \sin(\theta )/2=\sin(\theta /2)\cos(\theta /2)}$ ${\displaystyle 1=\nu ^{2}+\sin(\arccos(|\nu |))^{2}}$ ${\displaystyle \arccos(|\nu |)-|\nu |{\sqrt {1-\nu ^{2}}}}$

${\displaystyle \operatorname {OTF} (\nu )={\frac {2}{\pi }}\left(\arccos(|\nu |)-|\nu |{\sqrt {1-\nu ^{2}}}\right).}$

Se puede encontrar una discusión más detallada en ^[5] y ^{[2] : 152–153  .}

Evaluación numérica

La función de transferencia óptica unidimensional se puede calcular como la transformada de Fourier discreta de la función de propagación de línea. Estos datos se grafican en relación con los datos de frecuencia espacial . En este caso, se ajusta un polinomio de sexto orden a la curva de MTF en función de la frecuencia espacial para mostrar la tendencia. Se determina la frecuencia de corte del 50 % para obtener la frecuencia espacial correspondiente. De este modo, la posición aproximada del mejor enfoque de la unidad en prueba se determina a partir de estos datos.

Los datos MTF en función de la frecuencia espacial se normalizan ajustándoles un polinomio de sexto orden, lo que genera una curva suave. Se determina la frecuencia de corte del 50 % y se encuentra la frecuencia espacial correspondiente, lo que genera la posición aproximada del mejor enfoque .

La transformada de Fourier de la función de dispersión lineal (LSF) no se puede determinar analíticamente mediante las siguientes ecuaciones ^{[ cita requerida ]} :

${\displaystyle \operatorname {MTF} ={\mathcal {F}}\left[\operatorname {LSF} \right]\qquad \qquad \operatorname {MTF} =\int f(x)e^{-i2\pi \,xs}\,dx}$

Por lo tanto, la transformada de Fourier se aproxima numéricamente utilizando la transformada de Fourier discreta . ^[6] ${\displaystyle {\mathcal {DFT}}}$

${\displaystyle \operatorname {MTF} ={\mathcal {DFT}}[\operatorname {LSF} ]=Y_{k}=\sum _{n=0}^{N-1}y_{n}e^{-ik{\frac {2\pi }{N}}n}\qquad k\in [0,N-1]}$

dónde

• ${\displaystyle Y_{k}\,}$= el valor del MTF ${\displaystyle k^{\text{th}}}$
• ${\displaystyle N\,}$= número de puntos de datos
• ${\displaystyle n\,}$= índice
• ${\displaystyle k\,}$= término de los datos LSF ${\displaystyle k^{\text{th}}}$
• ${\displaystyle y_{n}\,}$= posición del píxel ${\displaystyle n^{\text{th}}\,}$
• ${\displaystyle i={\sqrt {-1}}}$

${\displaystyle e^{\pm ia}=\cos(a)\,\pm \,i\sin(a)}$

${\displaystyle \operatorname {MTF} ={\mathcal {DFT}}[\operatorname {LSF} ]=Y_{k}=\sum _{n=0}^{N-1}y_{n}\left[\cos \left(k{\frac {2\pi }{N}}n\right)-i\sin \left(k{\frac {2\pi }{N}}n\right)\right]\qquad k\in [0,N-1]}$

Luego se grafica el MTF frente a la frecuencia espacial y todos los datos relevantes relacionados con esta prueba se pueden determinar a partir de ese gráfico.

La función de transferencia vectorial

En aperturas numéricas altas como las que se encuentran en la microscopía, es importante considerar la naturaleza vectorial de los campos que transportan la luz. Al descomponer las ondas en tres componentes independientes correspondientes a los ejes cartesianos, se puede calcular una función de dispersión de puntos para cada componente y combinarlas en una función de dispersión de puntos vectorial . De manera similar, se puede determinar una función de transferencia óptica vectorial como se muestra en ( ^[7] ) y ( ^[8] ).

Medición

La función de transferencia óptica no sólo es útil para el diseño de sistemas ópticos, también es valiosa para caracterizar sistemas fabricados.

Partiendo de la función de propagación de puntos

La función de transferencia óptica se define como la transformada de Fourier de la respuesta al impulso del sistema óptico, también llamada función de dispersión de puntos . La función de transferencia óptica se obtiene fácilmente adquiriendo primero la imagen de una fuente puntual y aplicando la transformada de Fourier discreta bidimensional a la imagen muestreada. Dicha fuente puntual puede ser, por ejemplo, una luz brillante detrás de una pantalla con un orificio, una microesfera fluorescente o metálica o simplemente un punto pintado en una pantalla. El cálculo de la función de transferencia óptica a través de la función de dispersión de puntos es versátil, ya que puede caracterizar completamente la óptica con aberraciones cromáticas y de variación espacial repitiendo el procedimiento para varias posiciones y espectros de longitud de onda de la fuente puntual.

Uso de objetos de prueba extendidos para óptica invariante espacial

Cuando se puede suponer que las aberraciones son invariantes espacialmente, se pueden utilizar patrones alternativos para determinar la función de transferencia óptica, como líneas y bordes. Las funciones de transferencia correspondientes se denominan función de propagación de línea y función de propagación de borde, respectivamente. Estos objetos extendidos iluminan más píxeles en la imagen y pueden mejorar la precisión de la medición debido a la mayor relación señal-ruido. La función de transferencia óptica en este caso se calcula como la transformada de Fourier discreta bidimensional de la imagen y se divide por la del objeto extendido. Normalmente se utiliza una línea o un borde blanco y negro.

La función de propagación de línea

La transformada de Fourier bidimensional de una línea que pasa por el origen es una línea ortogonal a ella y que pasa por el origen. Por lo tanto, el divisor es cero para todas las dimensiones excepto una, por lo que la función de transferencia óptica solo se puede determinar para una sola dimensión utilizando una única función de propagación de línea (LSF). Si es necesario, la función de transferencia óptica bidimensional se puede determinar repitiendo la medición con líneas en varios ángulos.

La función de dispersión de línea se puede hallar utilizando dos métodos diferentes. Se puede hallar directamente a partir de una aproximación de línea ideal proporcionada por un objetivo de prueba de rendija o se puede derivar de la función de dispersión de borde, que se analiza en la siguiente subsección.

Función de propagación de bordes

La transformada de Fourier bidimensional de un borde también es distinta de cero únicamente en una única línea, ortogonal al borde. Esta función a veces se denomina función de dispersión de bordes (ESF). ^{[9] [10]} Sin embargo, los valores en esta línea son inversamente proporcionales a la distancia desde el origen. Aunque las imágenes de medición obtenidas con esta técnica iluminan una gran área de la cámara, esto beneficia principalmente la precisión a bajas frecuencias espaciales. Al igual que con la función de dispersión de líneas, cada medición solo determina un único eje de la función de transferencia óptica, por lo que son necesarias mediciones repetidas si no se puede suponer que el sistema óptico sea rotacionalmente simétrico.

Al evaluar el ESF , un operador define un área de cuadro equivalente al 10% ^{[ cita requerida ]} del área total del marco de un objetivo de prueba con borde de cuchillo retroiluminado por un cuerpo negro . El área se define para abarcar el borde de la imagen del objetivo.

Como se muestra en la figura de la derecha, un operador define un área de caja que abarca el borde de una imagen de objetivo de prueba con borde de cuchillo retroiluminada por un cuerpo negro . El área de la caja se define como aproximadamente el 10 % ^{[ cita requerida ]} del área total del marco. Los datos de píxeles de la imagen se traducen en una matriz bidimensional ( intensidad de píxeles y posición de píxeles). La amplitud (intensidad de píxeles) de cada línea dentro de la matriz se normaliza y se promedia. Esto produce la función de dispersión de bordes.

${\displaystyle \operatorname {ESF} ={\frac {X-\mu }{\sigma }}\qquad \qquad \sigma \,={\sqrt {\frac {\sum _{i=0}^{n-1}(x_{i}-\mu \,)^{2}}{n}}}\qquad \qquad \mu \,={\frac {\sum _{i=0}^{n-1}x_{i}}{n}}}$

dónde

• ESF = la matriz de salida de datos de intensidad de píxeles normalizados
• ${\displaystyle X\,}$= la matriz de entrada de datos de intensidad de píxeles
• ${\displaystyle x_{i}\,}$= el i- ^ésimo elemento de ${\displaystyle X\,}$
• ${\displaystyle \mu \,}$= el valor promedio de los datos de intensidad de píxeles
• ${\displaystyle \sigma \,}$= la desviación estándar de los datos de intensidad de píxeles
• ${\displaystyle n\,}$= número de píxeles utilizados en promedio

La función de dispersión de línea es idéntica a la primera derivada de la función de dispersión de borde ^[11] , que se deriva utilizando métodos numéricos . En caso de que sea más práctico medir la función de dispersión de borde, se puede determinar la función de dispersión de línea de la siguiente manera:

${\displaystyle \operatorname {LSF} ={\frac {d}{dx}}\operatorname {ESF} (x)}$

Normalmente, el ESF solo se conoce en puntos discretos, por lo que el LSF se aproxima numéricamente utilizando la diferencia finita :

${\displaystyle \operatorname {LSF} ={\frac {d}{dx}}\operatorname {ESF} (x)\approx {\frac {\Delta \operatorname {ESF} }{\Delta x}}}$

${\displaystyle \operatorname {LSF} \approx {\frac {\operatorname {ESF} _{i+1}-\operatorname {ESF} _{i-1}}{2(x_{i+1}-x_{i})}}}$

dónde:

• ${\displaystyle i\,}$= el índice ${\displaystyle i=1,2,\dots ,n-1}$
• ${\displaystyle x_{i}\,}$= posición del píxel ${\displaystyle i^{\text{th}}\,}$ ${\displaystyle i^{\text{th}}\,}$
• ${\displaystyle \operatorname {ESF} _{i}\,}$= ESF del píxel ${\displaystyle i^{\text{th}}\,}$

Usando una cuadrícula de líneas blancas y negras

Aunque la "nitidez" se suele medir con patrones de cuadrícula de líneas blancas y negras alternadas, se debe medir estrictamente utilizando una variación de onda sinusoidal de negro a blanco (una versión borrosa del patrón habitual). Cuando se utiliza un patrón de onda cuadrada (líneas simples blancas y negras), no solo existe un mayor riesgo de aliasing, sino que se debe tener en cuenta el hecho de que el componente fundamental de una onda cuadrada es mayor que la amplitud de la propia onda cuadrada (los componentes armónicos reducen la amplitud máxima). Por lo tanto, un gráfico de prueba de onda cuadrada mostrará resultados optimistas (mejor resolución de frecuencias espaciales altas de la que se logra realmente). El resultado de la onda cuadrada a veces se denomina "función de transferencia de contraste" (CTF).

Factores que afectan el MTF en sistemas de cámaras típicos

En la práctica, muchos factores provocan una borrosidad considerable en la imagen reproducida, de modo que los patrones con frecuencia espacial justo por debajo de la tasa de Nyquist pueden no ser visibles, y los patrones más finos pueden aparecer "descoloridos" como tonos de gris, no en blanco y negro. Un factor importante suele ser la imposibilidad de fabricar el filtro óptico "de pared de ladrillos" perfecto (que a menudo se realiza como una "placa de fase" o una lente con propiedades de borrosidad específicas en cámaras digitales y videocámaras). Un filtro de este tipo es necesario para reducir el aliasing eliminando frecuencias espaciales por encima de la tasa de Nyquist de la pantalla.

Sobremuestreo y conversión descendente para mantener la función de transferencia óptica

La única forma práctica de acercarse a la nitidez teórica posible en un sistema de imágenes digitales como una cámara es usar más píxeles en el sensor de la cámara que muestras en la imagen final y "convertir hacia abajo" o "interpolar" usando un procesamiento digital especial que corta las frecuencias altas por encima de la tasa de Nyquist para evitar el aliasing mientras se mantiene una MTF razonablemente plana hasta esa frecuencia. Este enfoque se adoptó por primera vez en la década de 1970 cuando se desarrollaron los escáneres de puntos volantes y, más tarde, los escáneres de línea CCD , que muestreaban más píxeles de los necesarios y luego los convertían hacia abajo, razón por la cual las películas siempre se han visto más nítidas en televisión que otro material grabado con una cámara de video. La única forma teóricamente correcta de interpolar o convertir hacia abajo es mediante el uso de un filtro espacial de paso bajo pronunciado, realizado por convolución con una función de ponderación sen( x )/ x bidimensional que requiere un procesamiento potente. En la práctica, se utilizan varias aproximaciones matemáticas a esto para reducir el requisito de procesamiento. Estas aproximaciones ahora se implementan ampliamente en sistemas de edición de video y en programas de procesamiento de imágenes como Photoshop .

De la misma manera que el vídeo de definición estándar con un MTF de alto contraste solo es posible con sobremuestreo, la televisión HD con una nitidez teórica total solo es posible si se parte de una cámara con una resolución significativamente mayor y se aplica un filtrado digital. Ahora que se graban películas en 4k e incluso en 8k para el cine, podemos esperar ver las mejores imágenes en HDTV solo en películas o material grabado con un estándar más alto. Por mucho que aumentemos el número de píxeles utilizados en las cámaras, esto siempre será así en ausencia de un filtro espacial óptico perfecto. De manera similar, una imagen de 5 megapíxeles obtenida con una cámara de 5 megapíxeles nunca puede ser más nítida que una imagen de 5 megapíxeles obtenida después de una conversión descendente con una cámara de 10 megapíxeles de la misma calidad. Debido al problema de mantener un MTF de alto contraste, las emisoras como la BBC consideraron durante mucho tiempo mantener la televisión de definición estándar, pero mejorar su calidad filmando y viendo con muchos más píxeles (aunque como se mencionó anteriormente, un sistema de este tipo, aunque impresionante, en última instancia carece del detalle muy fino que, aunque atenuado, mejora el efecto de la verdadera visualización en alta definición).

Otro factor en las cámaras y videocámaras digitales es la resolución de la lente. Se puede decir que una lente "resuelve" 1920 líneas horizontales, pero esto no significa que lo haga con modulación completa de negro a blanco. La "función de transferencia de modulación" (simplemente un término para la magnitud de la función de transferencia óptica sin tener en cuenta la fase) proporciona la verdadera medida del rendimiento de la lente y se representa mediante un gráfico de amplitud en función de la frecuencia espacial.

La difracción de la apertura de la lente también limita la MTF. Si bien reducir la apertura de una lente generalmente reduce las aberraciones y, por lo tanto, mejora la planitud de la MTF, existe una apertura óptima para cualquier tamaño de lente y sensor de imagen más allá de la cual las aperturas más pequeñas reducen la resolución debido a la difracción, que difunde la luz a través del sensor de imagen. Esto no era un problema en la época de las cámaras de placas e incluso de la película de 35 mm, pero se ha convertido en una limitación insuperable con los sensores de formato muy pequeño utilizados en algunas cámaras digitales y, especialmente, en las videocámaras. Las videocámaras de consumo HD de primera generación usaban sensores de 1/4 de pulgada, para los cuales las aperturas menores a f4 comienzan a limitar la resolución. Incluso las videocámaras profesionales usan principalmente sensores de 2/3 de pulgada, lo que prohíbe el uso de aperturas alrededor de f16 que se habrían considerado normales para formatos de película. Algunas cámaras (como la Pentax K10D ) cuentan con un modo de "exposición automática MTF", donde la elección de la apertura se optimiza para una máxima nitidez. Por lo general, esto significa algo en algún lugar en el medio del rango de apertura. ^[12]

Tendencia hacia las DSLR de gran formato y potencial MTF mejorado

Recientemente, se ha producido un cambio hacia el uso de cámaras réflex digitales de un solo objetivo de gran formato de imagen , impulsado por la necesidad de sensibilidad en condiciones de poca luz y efectos de profundidad de campo estrechos . Esto ha llevado a que algunos realizadores de programas de cine y televisión prefieran estas cámaras incluso a las cámaras de vídeo HD profesionales, debido a su potencial "fílmico". En teoría, el uso de cámaras con sensores de 16 y 21 megapíxeles ofrece la posibilidad de una nitidez casi perfecta mediante la conversión descendente dentro de la cámara, con filtrado digital para eliminar el aliasing. Estas cámaras producen resultados muy impresionantes y parecen estar liderando el camino en la producción de vídeo hacia la conversión descendente de gran formato, con el filtrado digital convirtiéndose en el enfoque estándar para la realización de un MTF plano con verdadera libertad de aliasing.

Inversión digital del OTF

Debido a los efectos ópticos, el contraste puede ser subóptimo y aproximarse a cero antes de alcanzar la frecuencia de Nyquist de la pantalla. La reducción del contraste óptico se puede revertir parcialmente amplificando digitalmente las frecuencias espaciales de forma selectiva antes de la visualización o el procesamiento posterior. Aunque existen procedimientos de restauración de imágenes digitales más avanzados, el algoritmo de deconvolución de Wiener se utiliza a menudo por su simplicidad y eficiencia. Dado que esta técnica multiplica los componentes espectrales espaciales de la imagen, también amplifica el ruido y los errores debidos, por ejemplo, al aliasing. Por lo tanto, solo es eficaz en grabaciones de buena calidad con una relación señal-ruido suficientemente alta.

Limitaciones

En general, la función de dispersión de puntos , la imagen de una fuente puntual, también depende de factores como la longitud de onda ( color ) y el ángulo de campo (posición lateral de la fuente puntual). Cuando dicha variación es suficientemente gradual, el sistema óptico podría caracterizarse mediante un conjunto de funciones de transferencia óptica. Sin embargo, cuando la imagen de la fuente puntual cambia abruptamente tras la traslación lateral, la función de transferencia óptica no describe el sistema óptico con precisión.

Véase también

• Bokeh
• Corrección gamma
• Contraste mínimo resoluble
• Diferencia de temperatura mínima resoluble
• Resolución óptica
• Relación señal-ruido
• Función de transferencia de señal
• Relación de Strehl
• Función de transferencia
• Codificación de frente de onda

Referencias

1. La definición exacta de resolución puede variar y a menudo se considera que es 1,22 veces mayor, según lo define el criterio de Rayleigh .
2. Williams, Charles S. (2002). Introducción a la función de transferencia óptica . SPIE – Sociedad Internacional de Ingeniería Óptica. ISBN 0-8194-4336-0.
3. "Función de transferencia de contraste" . Consultado el 16 de noviembre de 2013 .
4. Macias-Garza, F.; Bovik, A.; Diller, K.; Aggarwal, S.; Aggarwal, J. (1988). "El problema del cono faltante y la distorsión de paso bajo en la microscopía óptica de seccionamiento serial". ICASSP-88., Conferencia internacional sobre acústica, habla y procesamiento de señales . Vol. 2. págs. 890–893. doi :10.1109/ICASSP.1988.196731. S2CID  120191405.
5. Goodman, Joseph (2005). Introducción a la óptica de Fourier (3.ª ed.). Roberts & Co Publishers. ISBN 0-9747077-2-4.
6. Chapra, SC; Canale, RP (2006). Métodos numéricos para ingenieros (5.ª ed.). Nueva York, Nueva York: McGraw-Hill
7. Sheppard, CJR; Larkin, K. (1997). "Funciones pupilares vectoriales y funciones de transferencia vectorial" (PDF) . Optik-Stuttgart . 107 : 79–87.
8. Arnison, MR; Sheppard, CJR (2002). "Una función de transferencia óptica vectorial 3D adecuada para funciones pupilares arbitrarias". Optics Communications . 211 (1–6): 53–63. Bibcode :2002OptCo.211...53A. doi :10.1016/S0030-4018(02)01857-6.
9. Holst, GC (1998). Prueba y evaluación de sistemas de imágenes infrarrojas (2.ª ed.). Florida: JCD Publishing, Washington: SPIE.
10. "Prueba y medición – Productos – EOI". www.Electro-Optical.com . Archivado desde el original el 28 de agosto de 2008 . Consultado el 2 de enero de 2018 .
11. Mazzetta, JA; Scopatz, SD (2007). Pruebas automatizadas de sensores ultravioleta, visible e infrarrojo mediante óptica compartida. Sistemas de imágenes infrarrojas: análisis de diseño, modelado y pruebas XVIII, vol. 6543 , págs. 654313-1 654313-14
12. "B2BVideoSource.com: Terminología de cámaras". www.B2BVideoSource.com . Consultado el 2 de enero de 2018 .

Enlaces externos

• "Función de transferencia de modulación", por Glenn D. Boreman en SPIE Optipedia.
• "Cómo medir MTF y otras propiedades de las lentes", por Optikos Corporation.