Gran circulo

Análogo de geometría esférica de una línea recta

El círculo máximo g (verde) se encuentra en un plano que pasa por el centro de la esfera O (negro). La línea perpendicular a (violeta) que pasa por el centro se llama eje de g , y sus dos intersecciones con la esfera, P y P ' (rojo), son los polos de g . Cualquier círculo máximo s (azul) que pase por los polos es secundario a g .

Un gran círculo divide la esfera en dos hemisferios iguales.

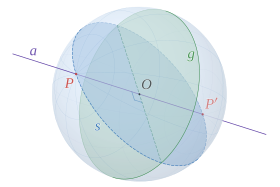
En matemáticas , un círculo máximo u ortódromo es la intersección circular de una esfera y un plano que pasa por el punto central de la esfera . ^{[1] [2]}

Discusión

Cualquier arco de un círculo máximo es una geodésica de la esfera, de modo que los círculos máximos en geometría esférica son el análogo natural de las líneas rectas en el espacio euclidiano . Para cualquier par de puntos distintos no antípodas en la esfera, hay un único círculo máximo que pasa por ambos. (Cada círculo máximo que pasa por cualquier punto también pasa por su punto antípoda, por lo que hay infinitos círculos máximos que pasan por dos puntos antípodas). El más corto de los dos arcos de círculo máximo entre dos puntos distintos en la esfera se llama arco menor , y es la trayectoria superficial más corta entre ellos. Su longitud de arco es la distancia del círculo máximo entre los puntos (la distancia intrínseca en una esfera), y es proporcional a la medida del ángulo central formado por los dos puntos y el centro de la esfera.

Un círculo máximo es el círculo más grande que se puede dibujar en una esfera dada. Cualquier diámetro de cualquier círculo máximo coincide con un diámetro de la esfera y, por lo tanto, cada círculo máximo es concéntrico con la esfera y comparte el mismo radio . Cualquier otro círculo de la esfera se llama círculo pequeño y es la intersección de la esfera con un plano que no pasa por su centro. Los círculos pequeños son el análogo de geometría esférica de los círculos en el espacio euclidiano.

Cada círculo en el espacio euclidiano tridimensional es un gran círculo de exactamente una esfera.

El disco delimitado por un círculo máximo se denomina disco máximo : es la intersección de una esfera y un plano que pasa por su centro. En dimensiones superiores, los círculos máximos de la n -esfera son la intersección de la n -esfera con 2-planos que pasan por el origen en el espacio euclidiano R ^{n + 1} .

La mitad de un gran círculo puede llamarse un gran semicírculo (por ejemplo, como en partes de un meridiano en astronomía ).

Derivación de caminos más cortos

Para demostrar que el arco menor de un círculo máximo es el camino más corto que une dos puntos en la superficie de una esfera, se le puede aplicar el cálculo de variaciones .

Considere la clase de todos los caminos regulares desde un punto a otro punto . Introduzca coordenadas esféricas de modo que coincida con el polo norte. Cualquier curva en la esfera que no intersecte ninguno de los polos, excepto posiblemente en los puntos finales, puede parametrizarse mediante ${\displaystyle p}$ ${\displaystyle q}$ ${\displaystyle p}$

${\displaystyle \theta =\theta (t),\quad \phi =\phi (t),\quad a\leq t\leq b}$

Se permite que el valor proporcionado adopte valores reales arbitrarios. La longitud de arco infinitesimal en estas coordenadas es ${\displaystyle \phi }$

${\displaystyle ds=r{\sqrt {\theta '^{2}+\phi '^{2}\sin ^{2}\theta }}\,dt.}$

Por lo tanto, la longitud de una curva de a es una función de la curva dada por ${\displaystyle \gamma }$ ${\displaystyle p}$ ${\displaystyle q}$

${\displaystyle S[\gamma ]=r\int _{a}^{b}{\sqrt {\theta '^{2}+\phi '^{2}\sin ^{2}\theta }}\,dt.}$

Según la ecuación de Euler-Lagrange , se minimiza si y sólo si ${\displaystyle S[\gamma ]}$

${\displaystyle {\frac {\sin ^{2}\theta \phi '}{\sqrt {\theta '^{2}+\phi '^{2}\sin ^{2}\theta }}}=C}$,

donde es una constante independiente, y ${\displaystyle C}$ ${\displaystyle t}$

${\displaystyle {\frac {\sin \theta \cos \theta \phi '^{2}}{\sqrt {\theta '^{2}+\phi '^{2}\sin ^{2}\theta }}}={\frac {d}{dt}}{\frac {\theta '}{\sqrt {\theta '^{2}+\phi '^{2}\sin ^{2}\theta }}}.}$

De la primera ecuación de estas dos, se puede obtener que

${\displaystyle \phi '={\frac {C\theta '}{\sin \theta {\sqrt {\sin ^{2}\theta -C^{2}}}}}}$.

Integrando ambos lados y considerando la condición de contorno, la solución real de es cero. Por lo tanto, y puede ser cualquier valor entre 0 y , lo que indica que la curva debe estar en un meridiano de la esfera. En un sistema de coordenadas cartesianas , esto es ${\displaystyle C}$ ${\displaystyle \phi '=0}$ ${\displaystyle \theta }$ ${\displaystyle \theta _{0}}$

${\displaystyle x\sin \phi _{0}-y\cos \phi _{0}=0}$

que es un plano que pasa por el origen, es decir, el centro de la esfera.

Aplicaciones

Algunos ejemplos de círculos máximos en la esfera celeste son el horizonte celeste , el ecuador celeste y la eclíptica . Los círculos máximos también se utilizan como aproximaciones bastante precisas de las geodésicas en la superficie de la Tierra para la navegación aérea o marítima (aunque no es una esfera perfecta ), así como en cuerpos celestes esferoidales .

El ecuador de la tierra idealizada es un círculo máximo y cualquier meridiano y su meridiano opuesto forman un círculo máximo. Otro círculo máximo es el que divide los hemisferios terrestre y acuático . Un círculo máximo divide la tierra en dos hemisferios y si un círculo máximo pasa por un punto debe pasar por su punto antípoda .

La transformada de Funk integra una función a lo largo de todos los grandes círculos de la esfera.

Véase también

• Gran elipse
• Línea de rumbo

Referencias

1. W., Weisstein, Eric. "Gran círculo - de Wolfram MathWorld". mathworld.wolfram.com . Consultado el 30 de septiembre de 2022 .{{cite web}}: CS1 maint: varios nombres: lista de autores ( enlace )
2. Weintrit, Adam; Kopcz, Piotr (2014). Loxodromia (línea loxodrómica), ortodromia (círculo máximo), gran elipse y línea geodésica (geodésica) en la navegación. EE. UU.: CRC Press, Inc. ISBN 978-1-138-00004-9.

Enlaces externos

• Gran círculo: de MathWorld Descripción, figuras y ecuaciones del Gran círculo. Mathworld, Wolfram Research, Inc. c1999
• Grandes círculos en el diagrama de Mercator por John Snyder con contribuciones adicionales de Jeff Bryant, Pratik Desai y Carl Woll, Wolfram Demonstrations Project .