Lógica difusa

Sistema para razonar sobre la vaguedad

La lógica difusa es una forma de lógica polivalente en la que el valor de verdad de las variables puede ser cualquier número real entre 0 y 1. Se emplea para manejar el concepto de verdad parcial, donde el valor de verdad puede variar entre completamente verdadero y completamente falso. ^[1] Por el contrario, en la lógica booleana , los valores de verdad de las variables solo pueden ser los valores enteros 0 o 1.

El término lógica difusa fue introducido con la propuesta de teoría de conjuntos difusos en 1965 por el matemático Lotfi Zadeh . ^{[2] [3]} Sin embargo, la lógica difusa había sido estudiada desde la década de 1920, como lógica de valor infinito , en particular por Łukasiewicz y Tarski . ^[4]

La lógica difusa se basa en la observación de que las personas toman decisiones basándose en información imprecisa y no numérica. Los modelos difusos o conjuntos difusos son medios matemáticos para representar la vaguedad y la información imprecisa (de ahí el término difuso). Estos modelos tienen la capacidad de reconocer, representar, manipular, interpretar y utilizar datos e información que son vagos y carecen de certeza. ^{[5] [6]}

La lógica difusa se ha aplicado a muchos campos, desde la teoría de control hasta la inteligencia artificial .

Descripción general

La lógica clásica sólo permite conclusiones que son verdaderas o falsas. Sin embargo, también hay proposiciones con respuestas variables, como las que se pueden encontrar al pedir a un grupo de personas que identifiquen un color. En tales casos, la verdad aparece como resultado de un razonamiento a partir de un conocimiento inexacto o parcial en el que las respuestas de la muestra se representan en un espectro. ^[7]

Tanto los grados de verdad como las probabilidades varían entre 0 y 1 y, por lo tanto, pueden parecer idénticos al principio, pero la lógica difusa utiliza los grados de verdad como un modelo matemático de vaguedad , mientras que la probabilidad es un modelo matemático de ignorancia . ^[8]

Aplicando valores de verdad

Una aplicación básica podría caracterizar varios subrangos de una variable continua . Por ejemplo, una medición de temperatura para frenos antibloqueo podría tener varias funciones de pertenencia independientes que definan rangos de temperatura particulares necesarios para controlar los frenos correctamente. Cada función asigna el mismo valor de temperatura a un valor de verdad en el rango de 0 a 1. Estos valores de verdad pueden usarse luego para determinar cómo deben controlarse los frenos. ^[9] La teoría de conjuntos difusos proporciona un medio para representar la incertidumbre.

Variables lingüísticas

En aplicaciones de lógica difusa, a menudo se utilizan valores no numéricos para facilitar la expresión de reglas y hechos. ^[10]

Una variable lingüística como la edad puede aceptar valores como joven y su antónimo viejo . Debido a que los lenguajes naturales no siempre contienen suficientes términos de valor para expresar una escala de valores difusos, es una práctica común modificar los valores lingüísticos con adjetivos o adverbios . Por ejemplo, podemos usar los setos rather y something para construir los valores adicionales rather old o something young . ^[11]

Sistemas difusos

Mamdani

El sistema más conocido es el basado en reglas Mamdani . ^[12] Utiliza las siguientes reglas:

1. Convierta todos los valores de entrada en funciones de pertenencia difusa.
2. Ejecute todas las reglas aplicables en la base de reglas para calcular las funciones de salida difusa.
3. Desfuzzifique las funciones de salida difusa para obtener valores de salida "nítidos".

Fuzzificación

La fuzzificación es el proceso de asignar la entrada numérica de un sistema a conjuntos difusos con cierto grado de pertenencia. Este grado de pertenencia puede estar en cualquier lugar dentro del intervalo [0,1]. Si es 0, entonces el valor no pertenece al conjunto difuso dado, y si es 1, entonces el valor pertenece completamente al conjunto difuso. Cualquier valor entre 0 y 1 representa el grado de incertidumbre de que el valor pertenece al conjunto. Estos conjuntos difusos se describen típicamente con palabras, y por lo tanto, al asignar la entrada del sistema a conjuntos difusos, podemos razonar con él de una manera lingüísticamente natural.

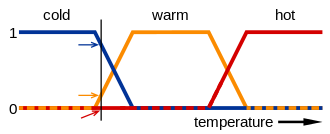
Por ejemplo, en la imagen de abajo, los significados de las expresiones cold , warm y hot están representados por funciones que representan una escala de temperatura. Un punto en esa escala tiene tres "valores de verdad", uno para cada una de las tres funciones. La línea vertical en la imagen representa una temperatura particular que miden las tres flechas (valores de verdad). Como la flecha roja apunta a cero, esta temperatura puede interpretarse como "no caliente"; es decir, esta temperatura tiene cero pertenencia al conjunto difuso "caliente". La flecha naranja (que apunta a 0,2) puede describirla como "ligeramente cálida" y la flecha azul (que apunta a 0,8) "bastante fría". Por lo tanto, esta temperatura tiene 0,2 pertenencia al conjunto difuso "cálido" y 0,8 pertenencia al conjunto difuso "frío". El grado de pertenencia asignado para cada conjunto difuso es el resultado de la fuzzificación.

Temperatura de lógica difusa

Los conjuntos difusos se definen a menudo como curvas en forma de triángulo o trapezoide, ya que cada valor tendrá una pendiente donde el valor aumenta, un pico donde el valor es igual a 1 (que puede tener una longitud de 0 o mayor) y una pendiente donde el valor disminuye. ^[13] También se pueden definir utilizando una función sigmoidea . ^[14] Un caso común es la función logística estándar definida como

${\displaystyle S(x)={\frac {1}{1+e^{-x}}}}$,

que tiene la siguiente propiedad de simetría

$${\displaystyle S(x)+S(-x)=1.}$$

De esto se deduce que

$${\displaystyle (S(x)+S(-x))\cdot (S(y)+S(-y))\cdot (S(z)+S(-z))=1}$$

Operadores de lógica difusa

La lógica difusa funciona con valores de pertenencia de una manera que imita la lógica booleana . Para ello, deben estar disponibles reemplazos para los operadores básicos ("puertas") AND, OR, NOT. Hay varias formas de hacerlo. Un reemplazo común se denominaOperador de Zadeh s:

Para VERDADERO/1 y FALSO/0, las expresiones difusas producen el mismo resultado que las expresiones booleanas.

Existen también otros operadores, de naturaleza más lingüística, llamados hedges , que pueden aplicarse. Se trata generalmente de adverbios como very o something , que modifican el significado de un conjunto mediante una fórmula matemática . ^[15]

Sin embargo, una tabla de elección arbitraria no siempre define una función de lógica difusa. En el artículo (Zaitsev, et al), ^[16] se ha formulado un criterio para reconocer si una tabla de elección dada define una función de lógica difusa y se ha propuesto un algoritmo simple de síntesis de funciones de lógica difusa basado en conceptos introducidos de constituyentes de mínimo y máximo. Una función de lógica difusa representa una disyunción de constituyentes de mínimo, donde un constituyente de mínimo es una conjunción de variables del área actual mayor o igual al valor de la función en esta área (a la derecha del valor de la función en la desigualdad, incluido el valor de la función).

Otro conjunto de operadores AND/OR se basa en la multiplicación, donde

x Y y = x*yNO x = 1 - xPor eso,x O y = NO( Y( NO(x), NO(y) ) )x O y = NO( Y(1-x, 1-y) )x O y = NO( (1-x)*(1-y) )x O y = 1-(1-x)*(1-y)x O y = x+y-xy

Dados dos casos cualesquiera de AND/OR/NOT, es posible derivar el tercero. La generalización de AND es una instancia de una norma t .

Reglas SI-ENTONCES

Las reglas IF-THEN asignan valores de verdad de entrada o calculados a valores de verdad de salida deseados. Ejemplo:

SI la temperatura ES muy fría ENTONCES fan_speed se detieneSI la temperatura ES fría ENTONCES la velocidad del ventilador es lentaSI la temperatura ES cálida ENTONCES la velocidad del ventilador es moderadaSI la temperatura es alta, ENTONCES la velocidad del ventilador es alta

Dada una cierta temperatura, la variable difusa caliente tiene un cierto valor de verdad, que se copia en la variable alta .

Si una variable de salida aparece en varias partes THEN, los valores de las respectivas partes IF se combinan utilizando el operador OR.

Desfuzzificación

El objetivo es obtener una variable continua a partir de valores de verdad difusos. ^{[ cita requerida ]}

Esto sería fácil si los valores de verdad de salida fueran exactamente los obtenidos a partir de la fuzzificación de un número dado. Sin embargo, dado que todos los valores de verdad de salida se calculan de forma independiente, en la mayoría de los casos no representan un conjunto de números de ese tipo. ^{[ cita requerida ]} Entonces, uno tiene que decidirse por un número que coincida mejor con la "intención" codificada en el valor de verdad. Por ejemplo, para varios valores de verdad de fan_speed, se debe encontrar una velocidad real que se ajuste mejor a los valores de verdad calculados de las variables 'slow', 'moderate', etc. ^{[ cita requerida ]}

No existe un algoritmo único para este propósito.

Un algoritmo común es

1. Para cada valor de verdad, corte la función de pertenencia en este valor
2. Combine las curvas resultantes utilizando el operador OR
3. Encuentra el centro de peso del área bajo la curva.
4. La posición x de este centro es entonces el resultado final.

Takagi-Sugeno-Kang (TSK)

El sistema TSK ^[17] es similar a Mamdani, pero el proceso de desfuzzificación está incluido en la ejecución de las reglas difusas. Estas también están adaptadas, de modo que en lugar de eso el consecuente de la regla se representa a través de una función polinómica (normalmente constante o lineal). Un ejemplo de regla con una salida constante sería:

SI la temperatura es muy fría = 2

En este caso, la salida será igual a la constante del consecuente (p. ej. 2). En la mayoría de los escenarios tendríamos una base de reglas completa, con 2 o más reglas. Si este es el caso, la salida de la base de reglas completa será el promedio del consecuente de cada regla i (Y _i ), ponderado de acuerdo con el valor de pertenencia de su antecedente (h _i ):

${\displaystyle {\frac {\sum _{i}(h_{i}\cdot Y_{i})}{\sum _{i}h_{i}}}}$

Un ejemplo de una regla con una salida lineal sería:

SI la temperatura ES muy fría Y la humedad ES alta = 2 * temperatura + 1 * humedad

En este caso, la salida de la regla será el resultado de la función en el consecuente. Las variables dentro de la función representan los valores de pertenencia después de la fuzzificación, no los valores nítidos. Al igual que antes, en caso de que tengamos una base de reglas completa con 2 o más reglas, la salida total será el promedio ponderado entre la salida de cada regla.

La principal ventaja de utilizar TSK en lugar de Mamdani es que es computacionalmente eficiente y funciona bien dentro de otros algoritmos, como el control PID y con algoritmos de optimización. También puede garantizar la continuidad de la superficie de salida. Sin embargo, Mamdani es más intuitivo y más fácil de usar para las personas. Por lo tanto, TSK se suele utilizar dentro de otros métodos complejos, como en sistemas de inferencia difusa neuroadaptativos .

Formación de un consenso de entradas y reglas difusas

Dado que la salida del sistema difuso es un consenso de todas las entradas y todas las reglas, los sistemas de lógica difusa pueden funcionar bien cuando los valores de entrada no están disponibles o no son confiables. Se pueden agregar ponderaciones opcionalmente a cada regla en la base de reglas y se pueden usar para regular el grado en que una regla afecta los valores de salida. Estas ponderaciones de reglas se pueden basar en la prioridad, confiabilidad o consistencia de cada regla. Estas ponderaciones de reglas pueden ser estáticas o pueden cambiarse dinámicamente, incluso en función de la salida de otras reglas.

Aplicaciones

La lógica difusa se utiliza en los sistemas de control para permitir que los expertos aporten reglas vagas como "si está cerca de la estación de destino y se mueve rápido, aumente la presión del freno del tren"; estas reglas vagas pueden luego refinarse numéricamente dentro del sistema.

Muchas de las primeras aplicaciones exitosas de la lógica difusa se implementaron en Japón. Una primera aplicación notable fue en la serie Sendai Subway 1000 , en la que la lógica difusa pudo mejorar la economía, la comodidad y la precisión del viaje. También se ha utilizado para el reconocimiento de escritura a mano en computadoras de bolsillo Sony, ayudas para el vuelo de helicópteros, controles del sistema de metro, mejora de la eficiencia de combustible de los automóviles, controles de lavadoras con un solo botón, controles automáticos de energía en aspiradoras y reconocimiento temprano de terremotos a través del Instituto de Sismología de la Oficina de Meteorología de Japón. ^[18]

Inteligencia artificial

Las redes neuronales basadas en inteligencia artificial y lógica difusa son, cuando se analizan, la misma cosa: la lógica subyacente de las redes neuronales es difusa. Una red neuronal tomará una variedad de entradas valiosas, les dará diferentes pesos en relación con las demás, combinará valores intermedios una cierta cantidad de veces y llegará a una decisión con un cierto valor. En ninguna parte de ese proceso hay nada parecido a las secuencias de decisiones de uno u otro que caracterizan las matemáticas no difusas, la programación informática y la electrónica digital . En la década de 1980, los investigadores estaban divididos sobre el enfoque más eficaz para el aprendizaje automático : el aprendizaje de árboles de decisión o las redes neuronales. El primer enfoque utiliza lógica binaria, que coincide con el hardware en el que se ejecuta, pero a pesar de los grandes esfuerzos, no dio como resultado sistemas inteligentes. Las redes neuronales, por el contrario, dieron como resultado modelos precisos de situaciones complejas y pronto encontraron su camino hacia una multitud de dispositivos electrónicos. ^[19] Ahora también se pueden implementar directamente en microchips analógicos, a diferencia de las implementaciones pseudoanalógicas anteriores en chips digitales. La mayor eficiencia de estos compensa la menor precisión intrínseca de lo analógico en diversos casos de uso.

Toma de decisiones médicas

La lógica difusa es un concepto importante en la toma de decisiones médicas . Dado que los datos médicos y de atención sanitaria pueden ser subjetivos o difusos, las aplicaciones en este ámbito tienen un gran potencial para beneficiarse mucho del uso de enfoques basados ​​en la lógica difusa.

La lógica difusa se puede utilizar en muchos aspectos diferentes dentro del marco de toma de decisiones médicas. Dichos aspectos incluyen ^{[20] [21] [22] [ aclaración necesaria ]} en el análisis de imágenes médicas , el análisis de señales biomédicas, la segmentación de imágenes ^[23] o señales y la extracción/selección de características de imágenes ^[23] o señales. ^[24]

La pregunta más importante en esta área de aplicación es cuánta información útil se puede obtener al utilizar la lógica difusa. Un desafío importante es cómo obtener los datos difusos necesarios. Esto es aún más complicado cuando uno tiene que obtener dichos datos de personas (generalmente, pacientes). Como se ha dicho

"El alcance de lo que se puede lograr y lo que no se puede lograr en el diagnóstico médico, irónicamente, es en sí mismo difuso"

—  Siete desafíos, 2019. ^[25]

Cómo obtener datos difusos y cómo validar la precisión de los datos es un trabajo en curso, estrechamente relacionado con la aplicación de la lógica difusa. El problema de evaluar la calidad de los datos difusos es difícil. Por eso, la lógica difusa es una posibilidad muy prometedora dentro del área de aplicación de la toma de decisiones médicas, pero aún se requiere más investigación para alcanzar su máximo potencial. ^[25]

Diagnóstico asistido por ordenador basado en imágenes

Una de las áreas de aplicación comunes de la lógica difusa es el diagnóstico asistido por computadora basado en imágenes en medicina. ^[26] El diagnóstico asistido por computadora es un conjunto computarizado de herramientas interrelacionadas que se pueden utilizar para ayudar a los médicos en la toma de decisiones diagnósticas.

Bases de datos difusas

Una vez definidas las relaciones difusas, es posible desarrollar bases de datos relacionales difusas . La primera base de datos relacional difusa, FRDB, apareció en la tesis de Maria Zemankova (1983). Posteriormente surgieron otros modelos como el modelo de Buckles-Petry, el modelo de Prade-Testemale, el modelo de Umano-Fukami o el modelo GEFRED de JM Medina, MA Vila et al.

Se han definido lenguajes de consulta difusa, como el SQLf de P. Bosc et al. y el FSQL de J. Galindo et al. Estos lenguajes definen algunas estructuras para incluir aspectos difusos en las sentencias SQL, como condiciones difusas, comparadores difusos, constantes difusas, restricciones difusas, umbrales difusos, etiquetas lingüísticas, etc.

Análisis lógico

En lógica matemática , existen varios sistemas formales de "lógica difusa", la mayoría de los cuales pertenecen a la familia de las lógicas difusas de norma t .

Lógica difusa proposicional

Las lógicas difusas proposicionales más importantes son:

• Lógica difusa proposicional basada en normas t monoidales La MTL es una axiomatización de la lógica donde la conjunción se define por una norma t continua izquierda y la implicación se define como el residuo de la norma t. Sus modelos corresponden a álgebras MTL que son redes conmutativas prelineales con residuos integrales acotados .
• La lógica difusa proposicional básica BL es una extensión de la lógica MTL, donde la conjunción se define mediante una norma t continua y la implicación también se define como el residuo de la norma t. Sus modelos corresponden a las álgebras BL.
• La lógica difusa de Łukasiewicz es una extensión de la lógica difusa básica BL, donde la conjunción estándar es la norma t de Łukasiewicz. Tiene los axiomas de la lógica difusa básica más un axioma de doble negación, y sus modelos corresponden a álgebras MV .
• La lógica difusa de Gödel es la extensión de la lógica difusa básica BL, donde la conjunción es la norma t de Gödel (es decir, el mínimo). Tiene los axiomas de BL más un axioma de idempotencia de conjunción, y sus modelos se denominan G-álgebras.
• La lógica difusa de producto es la extensión de la lógica difusa básica BL, donde la conjunción es la norma t del producto. Tiene los axiomas de BL más otro axioma de cancelatividad de la conjunción, y sus modelos se denominan álgebras de producto.
• La lógica difusa con sintaxis evaluada (a veces también llamada lógica de Pavelka), denotada por EVŁ, es una generalización adicional de la lógica difusa matemática. Mientras que los tipos de lógica difusa anteriores tienen una sintaxis tradicional y una semántica de múltiples valores, en EVŁ la sintaxis también se evalúa. Esto significa que cada fórmula tiene una evaluación. La axiomatización de EVŁ proviene de la lógica difusa de Łukasziewicz. Una generalización del teorema de completitud clásico de Gödel es demostrable en EVŁ ^{[ cita requerida ]} .

Lógica difusa de predicados

De manera similar a la forma en que la lógica de predicados se crea a partir de la lógica proposicional , las lógicas difusas de predicados extienden los sistemas difusos mediante cuantificadores universales y existenciales . La semántica del cuantificador universal en las lógicas difusas de norma t es el ínfimo de los grados de verdad de las instancias de la subfórmula cuantificada, mientras que la semántica del cuantificador existencial es el supremo del mismo.

Cuestiones de decidibilidad

Las nociones de "subconjunto decidible" y " subconjunto recursivamente enumerable " son básicas para las matemáticas clásicas y la lógica clásica . Por lo tanto, la cuestión de una extensión adecuada de ellas a la teoría de conjuntos difusos es crucial. La primera propuesta en tal dirección fue hecha por ES Santos con las nociones de máquina de Turing difusa , algoritmo difuso normal de Markov y programa difuso (ver Santos 1970). Sucesivamente, L. Biacino y G. Gerla argumentaron que las definiciones propuestas son bastante cuestionables. Por ejemplo, en ^[27] se muestra que las máquinas de Turing difusas no son adecuadas para la teoría del lenguaje difuso ya que hay lenguajes difusos naturales intuitivamente computables que no pueden ser reconocidos por una máquina de Turing difusa. Luego propusieron las siguientes definiciones. Denote por Ü el conjunto de números racionales en [0,1]. Entonces un subconjunto difuso s  : S  [0,1] de un conjunto S es recursivamente enumerable si existe una función recursiva h  : S × N Ü tal que, para cada x en S , la función h ( x , n ) es creciente con respecto a n y s ( x ) = lim h ( x , n ). Decimos que s es decidible si tanto s como su complemento – s son recursivamente enumerables. Es posible una extensión de dicha teoría al caso general de los L-subconjuntos (véase Gerla 2006). Las definiciones propuestas están bien relacionadas con la lógica difusa. De hecho, el siguiente teorema es válido (siempre que el aparato de deducción de la lógica difusa considerada satisfaga alguna propiedad de efectividad obvia). ${\displaystyle \rightarrow }$ ${\displaystyle \rightarrow }$

Toda teoría difusa "axiomatizable" es recursivamente enumerable. En particular, el conjunto difuso de fórmulas lógicamente verdaderas es recursivamente enumerable a pesar del hecho de que el conjunto preciso de fórmulas válidas no es recursivamente enumerable, en general. Además, toda teoría axiomatizable y completa es decidible.

Es una cuestión abierta dar soporte a una "tesis de Church" para las matemáticas difusas , la noción propuesta de enumerabilidad recursiva para subconjuntos difusos es la adecuada. Para resolver esto, es necesaria una extensión de las nociones de gramática difusa y máquina de Turing difusa . Otra cuestión abierta es partir de esta noción para encontrar una extensión de los teoremas de Gödel a la lógica difusa.

En comparación con otras lógicas

Probabilidad

La lógica difusa y la probabilidad abordan diferentes formas de incertidumbre. Si bien tanto la lógica difusa como la teoría de la probabilidad pueden representar grados de ciertos tipos de creencias subjetivas, la teoría de conjuntos difusos utiliza el concepto de pertenencia a conjuntos difusos, es decir, cuánto se encuentra una observación dentro de un conjunto vagamente definido, y la teoría de la probabilidad utiliza el concepto de probabilidad subjetiva , es decir, frecuencia de ocurrencia o probabilidad de algún evento o condición ^{[ aclaración necesaria ]} . El concepto de conjuntos difusos se desarrolló a mediados del siglo XX en Berkeley ^[28] como respuesta a la falta de una teoría de la probabilidad para modelar conjuntamente la incertidumbre y la vaguedad . ^[29]

Bart Kosko afirma en Fuzziness vs. Probability ^[30] que la teoría de la probabilidad es una subteoría de la lógica difusa, ya que las cuestiones de grados de creencia en la pertenencia a conjuntos mutuamente excluyentes en la teoría de la probabilidad pueden representarse como ciertos casos de pertenencia gradual no mutuamente excluyente en la teoría difusa. En ese contexto, también deriva el teorema de Bayes del concepto de subconjunto difuso. Lotfi A. Zadeh sostiene que la lógica difusa es diferente en carácter de la probabilidad, y no es un reemplazo para ella. Fuzzificó la probabilidad a probabilidad difusa y también la generalizó a la teoría de la posibilidad . ^[31]

De manera más general, la lógica difusa es una de las muchas extensiones diferentes de la lógica clásica destinadas a abordar cuestiones de incertidumbre fuera del alcance de la lógica clásica, la inaplicabilidad de la teoría de la probabilidad en muchos dominios y las paradojas de la teoría de Dempster-Shafer .

Ecorritmos

El teórico computacional Leslie Valiant usa el término ecorritos para describir cuántos sistemas y técnicas menos exactos como la lógica difusa (y la lógica "menos robusta") se pueden aplicar a los algoritmos de aprendizaje . Valiant esencialmente redefine el aprendizaje automático como evolutivo. En el uso general, los ecorritos son algoritmos que aprenden de sus entornos más complejos (de ahí eco- ) para generalizar, aproximar y simplificar la lógica de solución. Al igual que la lógica difusa, son métodos utilizados para superar variables continuas o sistemas demasiado complejos para enumerarlos por completo o comprenderlos de forma discreta o exacta. ^[32] Los ecorritos y la lógica difusa también tienen la propiedad común de tratar con posibilidades más que con probabilidades, aunque la retroalimentación y la alimentación hacia adelante , básicamente pesos estocásticos, son una característica de ambos cuando se trata, por ejemplo, con sistemas dinámicos .

Gödel G∞lógica

Otro sistema lógico en el que los valores de verdad son números reales entre 0 y 1 y en el que los operadores AND y OR se sustituyen por MIN y MAX es la lógica G _∞ de Gödel . Esta lógica tiene muchas similitudes con la lógica difusa, pero define la negación de forma diferente y tiene una implicación interna. La negación y la implicación se definen de la siguiente manera: ${\displaystyle \neg _{G}}$ ${\displaystyle {\xrightarrow[{G}]{}}}$

${\displaystyle {\begin{aligned}\neg _{G}u&={\begin{cases}1,&{\text{if }}u=0\\0,&{\text{if }}u>0\end{cases}}\\[3pt]u\mathrel {\xrightarrow[{G}]{}} v&={\begin{cases}1,&{\text{if }}u\leq v\\v,&{\text{if }}u>v\end{cases}}\end{aligned}}}$

lo que convierte al sistema lógico resultante en un modelo para la lógica intuicionista , haciéndolo particularmente bien comportado entre todas las posibles elecciones de sistemas lógicos con números reales entre 0 y 1 como valores de verdad. En este caso, la implicación puede interpretarse como "x es menos verdadero que y" y la negación como "x es menos verdadero que 0" o "x es estrictamente falso", y para cualquier y , tenemos que . En particular, en la lógica de Gödel la negación ya no es una involución y la doble negación asigna cualquier valor distinto de cero a 1. ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle AND(x,x\mathrel {\xrightarrow[{G}]{}} y)=AND(x,y)}$

Lógica difusa compensatoria

La lógica difusa compensatoria (CFL) es una rama de la lógica difusa con reglas modificadas para la conjunción y la disyunción. Cuando el valor de verdad de un componente de una conjunción o disyunción aumenta o disminuye, el otro componente disminuye o aumenta para compensar. Este aumento o disminución del valor de verdad puede compensarse con el aumento o la disminución de otro componente. Una compensación puede bloquearse cuando se alcanzan ciertos umbrales. Los defensores ^{[¿ quiénes? ]} afirman que la CFL permite mejores comportamientos semánticos computacionales e imita el lenguaje natural. ^{[ vago ] [33] [34]}

Según Jesús Cejas Montero (2011) La lógica difusa compensatoria está formada por cuatro operadores continuos: conjunción (c); disyunción (d); orden estricto difuso (o); y negación (n). La conjunción es la media geométrica y su dual como operadores conjuntivos y disyuntivos. ^[35]

Estandarización del lenguaje de marcado

El IEEE 1855 , el ESTÁNDAR IEEE 1855–2016, trata sobre un lenguaje de especificación llamado Fuzzy Markup Language (FML) ^[36] desarrollado por la IEEE Standards Association . FML permite modelar un sistema de lógica difusa de una manera legible para humanos e independiente del hardware. FML se basa en eXtensible Markup Language ( XML ). Los diseñadores de sistemas difusos con FML tienen una metodología unificada y de alto nivel para describir sistemas difusos interoperables. El ESTÁNDAR IEEE 1855–2016 utiliza el lenguaje de definición de esquema XML del W3C para definir la sintaxis y la semántica de los programas FML.

Antes de la introducción de FML, los profesionales de la lógica difusa podían intercambiar información sobre sus algoritmos difusos añadiendo a sus funciones de software la capacidad de leer, analizar correctamente y almacenar el resultado de su trabajo en una forma compatible con el lenguaje de control difuso (FCL) descrito y especificado por la Parte 7 de IEC 61131. [ ^{37] [38]}

Véase también

• Portal de filosofía
• Portal de psicología

• Inferencia bayesiana
• Sistema experto
• Falso dilema
• Análisis espacial arquitectónico difuso
• Clasificación difusa
• Concepto difuso
• Sistema de control difuso
• Electrónica difusa
• Subálgebra difusa
• CLIPS difusos
• Computación difusa de alto rendimiento
• Transacciones IEEE sobre sistemas difusos
• Elemento finito de intervalo
• Lógica basada en ruido
• Conjunto preliminar
• Paradoja de Sorites
• Lógica trinaria
• Conjuntos y sistemas difusos de tipo 2
• Lógica vectorial

Referencias

1. Novák, V.; Perfilieva, I.; Močkoř, J. (1999). Principios matemáticos de la lógica difusa . Dordrecht: Académico Kluwer. ISBN 978-0-7923-8595-0.
2. "Fuzzy Logic". Stanford Encyclopedia of Philosophy . Universidad Bryant. 23 de julio de 2006. Consultado el 30 de septiembre de 2008 .
3. Zadeh, LA (junio de 1965). "Conjuntos difusos". Información y control . 8 (3). San Diego: 338–353. doi : 10.1016/S0019-9958(65)90241-X . ISSN  0019-9958. Zbl  0139.24606. Wikidata  Q25938993.
4. Pelletier, Francis Jeffry (2000). "Revisión de la metamatemática de las lógicas difusas" (PDF) . The Bulletin of Symbolic Logic . 6 (3): 342–346. doi :10.2307/421060. JSTOR  421060. Archivado (PDF) desde el original el 3 de marzo de 2016.
5. "¿Qué es la lógica difusa? "Foro de discusión de ingeniería mecánica"". mechanicalsite.com . Archivado desde el original el 11 de noviembre de 2018 . Consultado el 11 de noviembre de 2018 .{{cite web}}: CS1 maint: unfit URL (link)
6. Babuška, Robert (1998). Modelado difuso para control. Springer Science & Business Media. ISBN 978-94-011-4868-9.
7. "Fuzzy Logic". YouTube . 9 de mayo de 2013. Archivado desde el original el 5 de diciembre de 2021 . Consultado el 11 de mayo de 2020 .
8. Asli, Kaveh Hariri; Aliyev, Soltan Ali Ogli; Thomas, Sabú; Gopakumar, Deepu A. (23 de noviembre de 2017). Manual de investigación de mecánica de fluidos y sólidos: teoría, simulación y experimento. Prensa CRC. ISBN 9781315341507.
9. Chaudhuri, Arindam; Mandaviya, Krupa; Badelia, Pratixa; Ghosh, Soumya K. (23 de diciembre de 2016). Sistemas de reconocimiento óptico de caracteres para diferentes idiomas con soft computing. Springer. ISBN 9783319502526.
10. Zadeh, LA; et al. (1996). Conjuntos difusos, lógica difusa, sistemas difusos . World Scientific Press. ISBN 978-981-02-2421-9.
11. Zadeh, LA (enero de 1975). "El concepto de variable lingüística y su aplicación al razonamiento aproximado—I". Ciencias de la información . 8 (3): 199–249. doi :10.1016/0020-0255(75)90036-5.
12. Mamdani, EH (1974). "Aplicación de algoritmos difusos para el control de plantas dinámicas simples". Actas de la Institución de Ingenieros Eléctricos . 121 (12): 1585–1588. doi :10.1049/PIEE.1974.0328.
13. Xiao, Zhi; Xia, Sisi; Gong, Ke; Li, Dan (1 de diciembre de 2012). "El conjunto blando difuso trapezoidal y su aplicación en MCDM". Modelado matemático aplicado . 36 (12): 5846–5847. doi : 10.1016/j.apm.2012.01.036 . ISSN  0307-904X.
14. Wierman, Mark J. "Introducción a las matemáticas de la incertidumbre: incluye teoría de conjuntos, lógica, probabilidad, conjuntos difusos, conjuntos aproximados y teoría de la evidencia" (PDF) . Universidad de Creighton. Archivado (PDF) desde el original el 30 de julio de 2012. Consultado el 16 de julio de 2016 .
15. Zadeh, LA (enero de 1972). "Una interpretación teórica de conjuntos difusos de los setos lingüísticos". Journal of Cybernetics . 2 (3): 4–34. doi :10.1080/01969727208542910. ISSN  0022-0280.
16. Zaitsev, DA; Sarbei, VG; Sleptsov, AI (1998). "Síntesis de funciones lógicas de valor continuo definidas en forma tabular". Cibernética y análisis de sistemas . 34 (2): 190–195. doi :10.1007/BF02742068. S2CID  120220846.
17. Takagi, Tomohiro; Sugeno, Michio (enero de 1985). "Identificación difusa de sistemas y sus aplicaciones al modelado y control". IEEE Transactions on Systems, Man, and Cybernetics . SMC-15 (1): 116–132. doi :10.1109/TSMC.1985.6313399. S2CID  3333100.
18. Bansod, Nitin A; Kulkarni, Marshall; Patil, SH (2005). "Soft Computing: un enfoque de lógica difusa". En Bharati Vidyapeeth College of Engineering (ed.). Soft Computing . Allied Publishers. pág. 73. ISBN 978-81-7764-632-0. Recuperado el 9 de noviembre de 2018 .
19. Elkan, Charles (1994). "El éxito paradójico de la lógica difusa". IEEE Expert . 9 (4): 3–49. CiteSeerX 10.1.1.100.8402 . doi :10.1109/64.336150. S2CID  113687. 
20. Lin, KP; Chang, HF; Chen, TL; Lu, YM; Wang, CH (2016). "Regresión C difusa intuicionista mediante regresión de vectores de soporte de mínimos cuadrados". Expert Systems with Applications . 64 : 296–304. doi :10.1016/j.eswa.2016.07.040.
21. Deng, H.; Deng, W.; Sun, X.; Ye, C.; Zhou, X. (2016). "Mejora intuicionista adaptativa difusa de imágenes de RM de tumores cerebrales". Scientific Reports . 6 : 35760. Bibcode :2016NatSR...635760D. doi : 10.1038/srep35760 . PMC 5082372 . PMID  27786240. 
22. Vlachos, IK; Sergiadis, GD (2007). "Información difusa intuicionista: aplicaciones al reconocimiento de patrones". Pattern Recognition Letters . 28 (2): 197–206. Código Bibliográfico :2007PaReL..28..197V. doi :10.1016/j.patrec.2006.07.004.
23. Gonzalez-Hidalgo, Manuel; Munar, Marc; Bibiloni, Pedro; Moya-Alcover, Gabriel; Craus-Miguel, Andrea; Segura-Sampedro, Juan Jose (octubre de 2019). "Detección de heridas infectadas en imágenes de cirugía abdominal utilizando lógica difusa y conjuntos difusos". 2019 International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob) . Barcelona, ​​España: IEEE. págs. 99–106. doi :10.1109/WiMOB.2019.8923289. ISBN . 978-1-7281-3316-4.S2CID208880793  .​
24. Das, S.; Guha, D.; Dutta, B. (2016). "Diagnóstico médico con la ayuda de la lógica difusa y la lógica difusa intuicionista". Inteligencia Aplicada . 45 (3): 850–867. doi :10.1007/s10489-016-0792-0. S2CID  14590409.
25. Yanase, Juri; Triantaphyllou, Evangelos (2019). "Los siete desafíos clave para el futuro del diagnóstico asistido por computadora en medicina". Revista internacional de informática médica . 129 : 413–422. doi :10.1016/j.ijmedinf.2019.06.017. PMID  31445285. S2CID  198287435.
26. Yanase, Juri; Triantaphyllou, Evangelos (2019). "Un estudio sistemático del diagnóstico asistido por ordenador en medicina: desarrollos pasados ​​y presentes". Sistemas expertos con aplicaciones . 138 : 112821. doi :10.1016/j.eswa.2019.112821. S2CID  199019309.
27. Gerla, G. (2016). "Comentarios sobre algunas teorías de computación difusa". Revista Internacional de Sistemas Generales . 45 (4): 372–392. Bibcode :2016IJGS...45..372G. doi :10.1080/03081079.2015.1076403. S2CID  22577357.
28. "Lotfi Zadeh Berkeley". Archivado desde el original el 11 de febrero de 2017.
29. Mares, Milán (2006). "Conjuntos difusos". Scholarpedia . 1 (10): 2031. Código Bibliográfico :2006SchpJ...1.2031M. doi : 10.4249/scholarpedia.2031 .
30. Kosko, Bart . «Fuzziness vs. Probability» (PDF) . Universidad del Sur de California. Archivado (PDF) del original el 2 de septiembre de 2006. Consultado el 9 de noviembre de 2018 .
31. Novák, V (2005). "¿Son los conjuntos difusos una herramienta razonable para modelar fenómenos vagos?". Fuzzy Sets and Systems . 156 (3): 341–348. doi :10.1016/j.fss.2005.05.029.
32. Valiant, Leslie (2013). Probablemente aproximadamente correcto: algoritmos de la naturaleza para aprender y prosperar en un mundo complejo . Nueva York: Basic Books. ISBN 978-0465032716.
33. Richardson, Mark (2010). "6.863 Final Project Writeup" (PDF) . Archivado (PDF) del original el 4 de octubre de 2015. Consultado el 2 de octubre de 2015 .
34. Veri, Francesco (2017). "Condiciones difusas de atributos múltiples en fsQCA: problemas y soluciones". Métodos sociológicos e investigación . 49 (2): 312–355. doi :10.1177/0049124117729693. S2CID  125146607.
35. Montero, Jesús Cejas (2011). "La lógica difusa compensatoria" [La lógica difusa compensatoria]. Ingeniería Industrial (en español). 32 (2): 157–162. Vendaval  A304726398.
36. Acampora, Giovanni; Di Stefano, Bruno; Vitiello, Autilia (noviembre de 2016). "IEEE 1855™: El primer estándar IEEE patrocinado por la IEEE Computational Intelligence Society [Resumen de la sociedad]". Revista IEEE Computational Intelligence . 11 (4): 4–6. doi :10.1109/MCI.2016.2602068.
37. Di Stefano, Bruno N. (2013). "Sobre la necesidad de un lenguaje estándar para diseñar sistemas difusos". Sobre el poder del lenguaje de marcado difuso . Estudios sobre borrosidad y computación blanda. Vol. 296. págs. 3–15. doi :10.1007/978-3-642-35488-5_1. ISBN 978-3-642-35487-8.
38. Sobre el poder del lenguaje de marcado difuso . Estudios sobre borrosidad y computación blanda. Vol. 296. 2013. doi :10.1007/978-3-642-35488-5. ISBN 978-3-642-35487-8.

Bibliografía

• Arabacioglu, BC (2010). "Uso de un sistema de inferencia difusa para el análisis del espacio arquitectónico". Applied Soft Computing . 10 (3): 926–937. doi :10.1016/j.asoc.2009.10.011.
• Biacino, Loredana; Gerla, Giangiacomo (1 de octubre de 2002). "Lógica difusa, continuidad y efectividad". Archivo de Lógica Matemática . 41 (7): 643–667. CiteSeerX  10.1.1.2.8029 . doi :10.1007/s001530100128. S2CID  12513452.
• Cox, Earl (1994). Manual de sistemas difusos: guía para profesionales sobre cómo construir, usar y mantener sistemas difusos . Boston: AP Professional. ISBN 978-0-12-194270-0.
• Gerla, Giangiacomo (marzo de 2006). "Efectividad y lógicas multivaluadas". Journal of Symbolic Logic . 71 (1): 137–162. doi :10.2178/jsl/1140641166. S2CID  12322009.
• Hájek, Petr (1998). Metamatemáticas de la lógica difusa . Dordrecht: Kluwer. ISBN 978-0-7923-5238-9.
• Hájek, Petr (agosto de 1995). "Lógica difusa y jerarquía aritmética". Fuzzy Sets and Systems . 73 (3): 359–363. doi :10.1016/0165-0114(94)00299-M.
• Halpern, Joseph Y. (2003). Razonamiento sobre la incertidumbre . Cambridge, Massachusetts: MIT Press . ISBN 978-0-262-08320-1.
• Höppner, Frank; Klawonn, F.; Kruse, R .; Runkler, T. (1999). Análisis de conglomerados difusos: métodos para la clasificación, el análisis de datos y el reconocimiento de imágenes . Nueva York: John Wiley. ISBN 978-0-471-98864-9.
• Ibrahim, Ahmad M. (1997). Introducción a la electrónica difusa aplicada . Englewood Cliffs, NJ: Prentice Hall . ISBN 978-0-13-206400-2.
• Klir, George Jiří ; Folger, Tina A. (1988). Conjuntos difusos, incertidumbre e información. Englewood Cliffs, NJ: Prentice Hall . ISBN 978-0-13-345984-5.
• Klir, George Jiří ; St. Clair, Ute H.; Yuan, Bo (1997). Teoría de conjuntos difusos: fundamentos y aplicaciones . Englewood Cliffs, NJ: Prentice Hall . ISBN 978-0-13-341058-7.
• Klir, George Jiří ; Yuan, Bo (1995). Conjuntos difusos y lógica difusa: teoría y aplicaciones . Upper Saddle River, NJ: Prentice Hall PTR . ISBN 978-0-13-101171-7.
• Kosko, Bart (1993). Pensamiento difuso: la nueva ciencia de la lógica difusa. Nueva York: Hyperion. ISBN 978-0-7868-8021-8.
• Kosko, Bart; Isaka, Satoru (julio de 1993). "Fuzzy Logic". Scientific American . 269 (1): 76–81. Código Bibliográfico :1993SciAm.269a..76K. doi :10.1038/scientificamerican0793-76.
• Lohani, AK; Goel, NK; Bhatia, KKS (2006). "Sistema de inferencia difusa Takagi-Sugeno para modelar la relación caudal-nivel". Revista de hidrología . 331 (1): 146–160. Código Bibliográfico :2006JHyd..331..146L. doi :10.1016/j.jhydrol.2006.05.007.
• Lohani, AK; Goel, NK; Bhatia, KKS (2007). "Obtención de relaciones de nivel-descarga-concentración de sedimentos mediante lógica difusa". Revista de Ciencias Hidrológicas . 52 (4): 793–807. Código Bibliográfico :2007HydSJ..52..793L. doi :10.1623/hysj.52.4.793. S2CID  117782707.
• Lohani, AK; Goel, NK; Bhatia, KKS (2012). "Modelado hidrológico de series temporales: una comparación entre técnicas adaptativas neurodifusas, de redes neuronales y autorregresivas". Journal of Hydrology . 442–443 (6): 23–35. Bibcode :2012JHyd..442...23L. doi :10.1016/j.jhydrol.2012.03.031.
• Masmoudi, Malek; Haït, Alain (noviembre de 2012). "Modelado de incertidumbre difusa para la planificación de proyectos; aplicación al mantenimiento de helicópteros" (PDF) . Revista internacional de investigación en producción . 50 (24). Archivado (PDF) desde el original el 22 de septiembre de 2017.
• Merigó, José M.; Gil-Lafuente, Anna M.; Yager, Ronald R. (febrero de 2015). "Una visión general de la investigación difusa con indicadores bibliométricos". Applied Soft Computing . 27 : 420–433. doi :10.1016/j.asoc.2014.10.035.
• Mironov, AM (agosto de 2005). "Lógicas modales difusas". Revista de ciencias matemáticas . 128 (6): 3461–3483. doi : 10.1007/s10958-005-0281-1 . S2CID  120674564.
• Montaña, Franco (2001). "Tres problemas de complejidad en lógica difusa cuantificada". Estudios Lógica . 68 (1): 143-152. doi :10.1023/A:1011958407631. S2CID  20035297.
• Mundici, Daniele; Cignoli, Roberto; D'Ottaviano, Itala ML (1999). Fundamentos algebraicos del razonamiento polivalente . Dordrecht: Académico Kluwer. ISBN 978-0-7923-6009-4.
• Novák, Vilém (1989). Conjuntos difusos y sus aplicaciones . Bristol: Adam Hilger. ISBN 978-0-85274-583-0.
• Novák, Vilém (2005). "Sobre la teoría de tipos difusos". Conjuntos y sistemas difusos . 149 (2): 235–273. doi :10.1016/j.fss.2004.03.027.
• Novák, Vilém; Perfilieva, Irina; Močkoř, Jiří (1999). Principios matemáticos de la lógica difusa . Dordrecht: Académico Kluwer. ISBN 978-0-7923-8595-0.
• Onses, Richard (1996). Experton de segundo orden: una nueva herramienta para cambiar paradigmas en el cálculo del riesgo país . Universidad, Secretariado de Publicaciones. ISBN 978-84-7719-558-0.
• Onsés, Richard (1994). Determinación de la incertidumbre inherente a las inversiones en América Latina sobre la base de la teoría de los sous ensembles flous . Barcelona. ISBN 978-84-475-0881-5.{{cite book}}: CS1 maint: location missing publisher (link)
• Passino, Kevin M.; Yurkovich, Stephen (1998). Control difuso. Boston: Addison-Wesley . ISBN 978-0-201-18074-9.
• Pedrycz, Witold; Gomide, Fernando (2007). Ingeniería de sistemas difusos: hacia una computación centrada en el ser humano . Hoboken: Wiley-Interscience . ISBN 978-0-471-78857-7.
• Pao-Ming, Pu ; Ying-Ming, Liu (agosto de 1980). "Topología difusa. I. Estructura de vecindad de un punto difuso y convergencia de Moore-Smith". Revista de análisis matemático y aplicaciones . 76 (2): 571–599. doi : 10.1016/0022-247X(80)90048-7 .
• Sahoo, Bhabagrahi; Lohani, AK; Sahu, Rohit K. (2006). "Modelos de gestión basados ​​en programación lineal y multiobjetivo difuso para la planificación óptima de sistemas tierra-agua-cultivo". Water Resources Management . 20 (6): 931–948. Bibcode :2006WatRM..20..931S. doi :10.1007/s11269-005-9015-x. S2CID  154264034.
• Santos, Eugene S. (1970). "Algoritmos difusos". Información y control . 17 (4): 326–339. doi : 10.1016/S0019-9958(70)80032-8 .
• Scarpellini, Bruno (junio de 1962). "Die nichtaxiomatisierbarkeit des unendlichwertigen Prädikatenkalküls von Łukasiewicz". Revista de Lógica Simbólica . 27 (2): 159-170. doi :10.2307/2964111. hdl : 20.500.11850/423097 . JSTOR  2964111. S2CID  26330059.
• Seising, Rudolf (2007). La fuzzificación de los sistemas. La génesis de la teoría de conjuntos difusos y sus aplicaciones iniciales: desarrollos hasta la década de 1970. Springer-Verlag. ISBN 978-3-540-71795-9.
• Steeb, Willi-Hans (2008). The Nonlinear Workbook: Chaos, Fractals, Cellular Autómatas, Neural Networks, Genetic Algorithms, Gene Expression Programming, Support Vector Machine, Wavelets, Hidden Markov Models, Fuzzy Logic with C++, Java and SymbolicC++ Programs (4.ª edición). World Scientific. ISBN 978-981-281-852-2.
• Tsitolovsky, Lev; Sandler, Uziel (2008). Comportamiento de células neuronales y lógica difusa . Springer. ISBN 978-0-387-09542-4.
• Wiedermann, J. (2004). "Caracterización de la potencia computacional super-Turing y la eficiencia de las máquinas de Turing difusas clásicas". Ciencias de la Computación Teórica . 317 (1–3): 61–69. doi : 10.1016/j.tcs.2003.12.004 .
• Yager, Ronald R.; Filev, Dimitar P. (1994). Fundamentos de modelado y control difusos . Nueva York: Wiley. ISBN 978-0-471-01761-5.
• Van Pelt, Miles (2008). Lógica difusa aplicada a la vida cotidiana . Seattle, WA: No No No No Press. ISBN 978-0-252-16341-8.
• Von Altrock, Constantin (1995). Explicación de las aplicaciones de la lógica difusa y NeuroFuzzy . Upper Saddle River, NJ: Prentice Hall PTR. ISBN 978-0-13-368465-0.
• Wilkinson, RH (1963). "Un método para generar funciones de varias variables utilizando lógica de diodos analógicos". IEEE Transactions on Electronic Computers . 12 (2): 112–129. doi :10.1109/PGEC.1963.263419.
• Zadeh, LA (febrero de 1968). "Algoritmos difusos". Información y control . 12 (2): 94–102. doi : 10.1016/S0019-9958(68)90211-8 .
• Zadeh, LA (junio de 1965). "Conjuntos difusos". Información y control . 8 (3). San Diego: 338–353. doi : 10.1016/S0019-9958(65)90241-X . ISSN  0019-9958. Zbl  0139.24606. Wikidata  Q25938993.
• Zaitsev, DA; Sarbei, VG; Sleptsov, AI (1998). "Síntesis de funciones lógicas de valor continuo definidas en forma tabular". Cibernética y análisis de sistemas . 34 (2): 190–195. doi :10.1007/BF02742068. S2CID  120220846.
• Zimmermann, H. (2001). Teoría de conjuntos difusos y sus aplicaciones . Boston: Kluwer Academic Publishers . ISBN. 978-0-7923-7435-0.

Enlaces externos

• IEC 1131-7 CD1 Archivado el 4 de marzo de 2021 en Wayback Machine. IEC 1131-7 CD1 PDF
• Lógica difusa: artículo en Scholarpedia
• Modelado con palabras: artículo en Scholarpedia
• Lógica difusa: artículo en la Enciclopedia de Filosofía de Stanford
• Matemáticas difusas: introducción a la lógica difusa para principiantes
• Imprecisión y exactitud: imprecisión en la vida cotidiana, la ciencia, la religión, la ética, la política, etc.
• Fuzzylite: una biblioteca de control de lógica difusa multiplataforma, gratuita y de código abierto escrita en C++. También tiene una interfaz gráfica de usuario muy útil en QT4.
• Aprendizaje automático más flexible: MIT describe una aplicación.
• Similitud semántica Archivado el 4 de octubre de 2015 en Wayback Machine. El MIT proporciona detalles sobre la similitud semántica difusa.