Un átomo de hidrógeno es un átomo del elemento químico hidrógeno . El átomo eléctricamente neutro contiene un único protón con carga positiva y un único electrón con carga negativa unidos al núcleo por la fuerza de Coulomb . El hidrógeno atómico constituye aproximadamente el 75% de la masa bariónica del universo. [1]
En la vida cotidiana en la Tierra, los átomos de hidrógeno aislados (llamados "hidrógeno atómico") son extremadamente raros. En cambio, un átomo de hidrógeno tiende a combinarse con otros átomos en compuestos, o con otro átomo de hidrógeno para formar gas hidrógeno ordinario ( diatómico ), H2 . "Hidrógeno atómico" y "átomo de hidrógeno" en el uso común del inglés tienen significados superpuestos, aunque distintos. Por ejemplo, una molécula de agua contiene dos átomos de hidrógeno, pero no contiene hidrógeno atómico (lo que se referiría a átomos de hidrógeno aislados).
La espectroscopia atómica muestra que existe un conjunto infinito y discreto de estados en los que puede existir un átomo de hidrógeno (o cualquier otro), contrariamente a las predicciones de la física clásica . Los intentos de desarrollar una comprensión teórica de los estados del átomo de hidrógeno han sido importantes para la historia de la mecánica cuántica , ya que todos los demás átomos pueden entenderse de manera aproximada conociendo en detalle esta estructura atómica más simple.
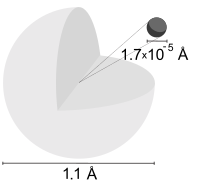
El isótopo más abundante , el hidrógeno-1 , protio o hidrógeno ligero , no contiene neutrones y es simplemente un protón y un electrón . El protio es estable y constituye el 99,985% de los átomos de hidrógeno naturales. [2]
Deuterium (2H) contains one neutron and one proton in its nucleus. Deuterium is stable and makes up 0.0156% of naturally occurring hydrogen[2] and is used in industrial processes like nuclear reactors and Nuclear Magnetic Resonance.
Tritium (3H) contains two neutrons and one proton in its nucleus and is not stable, decaying with a half-life of 12.32 years. Because of its short half-life, tritium does not exist in nature except in trace amounts.
Heavier isotopes of hydrogen are only created artificially in particle accelerators and have half-lives on the order of 10−22 seconds. They are unbound resonances located beyond the neutron drip line; this results in prompt emission of a neutron.
The formulas below are valid for all three isotopes of hydrogen, but slightly different values of the Rydberg constant (correction formula given below) must be used for each hydrogen isotope.
Lone neutral hydrogen atoms are rare under normal conditions. However, neutral hydrogen is common when it is covalently bound to another atom, and hydrogen atoms can also exist in cationic and anionic forms.
If a neutral hydrogen atom loses its electron, it becomes a cation. The resulting ion, which consists solely of a proton for the usual isotope, is written as "H+" and sometimes called hydron. Free protons are common in the interstellar medium, and solar wind. In the context of aqueous solutions of classical Brønsted–Lowry acids, such as hydrochloric acid, it is actually hydronium, H3O+, that is meant. Instead of a literal ionized single hydrogen atom being formed, the acid transfers the hydrogen to H2O, forming H3O+.
If instead a hydrogen atom gains a second electron, it becomes an anion. The hydrogen anion is written as "H–" and called hydride.
The hydrogen atom has special significance in quantum mechanics and quantum field theory as a simple two-body problem physical system which has yielded many simple analytical solutions in closed-form.
Los experimentos realizados por Ernest Rutherford en 1909 demostraron que la estructura del átomo era un núcleo denso y positivo con una tenue nube de carga negativa a su alrededor. Esto inmediatamente generó dudas sobre cómo un sistema así podría ser estable. El electromagnetismo clásico había demostrado que cualquier carga acelerada irradia energía, como lo demuestra la fórmula de Larmor . Si se supone que el electrón orbita en un círculo perfecto e irradia energía continuamente, el electrón rápidamente entraría en espiral hacia el núcleo con un tiempo de caída de: [3]
En 1913, Niels Bohr obtuvo los niveles de energía y las frecuencias espectrales del átomo de hidrógeno después de hacer una serie de suposiciones simples para corregir el fallido modelo clásico. Los supuestos incluían:
Bohr supuso que el momento angular del electrón está cuantificado con valores posibles:
Para , el valor [5]
El valor exacto de la constante de Rydberg supone que el núcleo es infinitamente masivo con respecto al electrón. Para el hidrógeno-1, el hidrógeno-2 ( deuterio ) y el hidrógeno-3 ( tritio ) que tienen masa finita, la constante debe modificarse ligeramente para utilizar la masa reducida del sistema, en lugar de simplemente la masa del electrón. Esto incluye la energía cinética del núcleo en el problema, porque la energía cinética total (electrón más nuclear) es equivalente a la energía cinética de la masa reducida que se mueve con una velocidad igual a la velocidad del electrón con respecto al núcleo. Sin embargo, como el núcleo es mucho más pesado que el electrón, la masa del electrón y la masa reducida son casi iguales. La constante de Rydberg R M para un átomo de hidrógeno (un electrón), R está dada por
Todavía había problemas con el modelo de Bohr:
La mayoría de estas deficiencias se resolvieron mediante la modificación del modelo de Bohr realizada por Arnold Sommerfeld . Sommerfeld introdujo dos grados de libertad adicionales, permitiendo que un electrón se moviera en una órbita elíptica caracterizada por su excentricidad y declinación con respecto a un eje elegido. Esto introdujo dos números cuánticos adicionales, que corresponden al momento angular orbital y su proyección sobre el eje elegido. De este modo se encontró la multiplicidad correcta de estados (excepto el factor 2 que explica el espín del electrón aún desconocido). Además, aplicando la relatividad especial a las órbitas elípticas, Sommerfeld logró derivar la expresión correcta para la estructura fina de los espectros del hidrógeno (que resulta ser exactamente la misma que en la teoría de Dirac más elaborada). Sin embargo, algunos fenómenos observados, como el anómalo efecto Zeeman , quedaron sin explicación. Estas cuestiones se resolvieron con el pleno desarrollo de la mecánica cuántica y la ecuación de Dirac . A menudo se alega que la ecuación de Schrödinger es superior a la teoría de Bohr-Sommerfeld a la hora de describir el átomo de hidrógeno. Este no es el caso, ya que la mayoría de los resultados de ambos enfoques coinciden o son muy cercanos (una excepción notable es el problema del átomo de hidrógeno en campos eléctricos y magnéticos cruzados, que no puede resolverse de manera consistente en el marco de la teoría de Bohr). teoría de Sommerfeld), y en ambas teorías las principales deficiencias se deben a la ausencia del espín del electrón. Fue el completo fracaso de la teoría de Bohr-Sommerfeld para explicar los sistemas de muchos electrones (como el átomo de helio o la molécula de hidrógeno) lo que demostró su insuficiencia para describir los fenómenos cuánticos.
La ecuación de Schrödinger permite calcular los estados estacionarios y también la evolución temporal de los sistemas cuánticos. Se dispone de respuestas analíticas exactas para el átomo de hidrógeno no relativista. Antes de pasar a presentar un relato formal, aquí damos una descripción general elemental.
Dado que el átomo de hidrógeno contiene un núcleo y un electrón, la mecánica cuántica permite predecir la probabilidad de encontrar el electrón a cualquier distancia radial dada . Está dada por el cuadrado de una función matemática conocida como " función de onda ", que es una solución de la ecuación de Schrödinger. El estado de equilibrio energético más bajo del átomo de hidrógeno se conoce como estado fundamental. La función de onda del estado fundamental se conoce como función de onda. Está escrito como:
Aquí está el valor numérico del radio de Bohr. La densidad de probabilidad de encontrar el electrón a una distancia en cualquier dirección radial es el valor al cuadrado de la función de onda:
La función de onda es esféricamente simétrica y el área de superficie de una capa a una distancia es , por lo que la probabilidad total de que el electrón esté en una capa a una distancia y un espesor es
Resulta que este es un máximo en . Es decir, la imagen de Bohr de un electrón que orbita alrededor del núcleo en un radio corresponde al radio más probable. En realidad, existe una probabilidad finita de que el electrón pueda encontrarse en cualquier lugar , siendo la probabilidad indicada por el cuadrado de la función de onda. Dado que la probabilidad de encontrar el electrón en algún lugar de todo el volumen es la unidad, la integral de es la unidad. Entonces decimos que la función de onda está correctamente normalizada.
Como se analiza a continuación, el estado fundamental también está indicado por los números cuánticos . Los segundos estados de energía más bajos, justo por encima del estado fundamental, están dados por los números cuánticos , y . Todos estos estados tienen la misma energía y se conocen como estados y . Hay un estado:
Es más probable que un electrón en el estado o se encuentre en la segunda órbita de Bohr con energía dada por la fórmula de Bohr.
El hamiltoniano del átomo de hidrógeno es el operador de energía cinética radial y la fuerza de atracción de Coulomb entre el protón positivo y el electrón negativo. Usando la ecuación de Schrödinger independiente del tiempo, ignorando todas las interacciones de acoplamiento de espín y usando la masa reducida , la ecuación se escribe como:
Ampliando el laplaciano en coordenadas esféricas:
Esta es una ecuación diferencial parcial separable que se puede resolver en términos de funciones especiales. Cuando la función de onda se separa como producto de las funciones , y aparecen tres funciones diferenciales independientes [6] siendo A y B las constantes de separación:
Las funciones de onda de posición normalizadas , dadas en coordenadas esféricas, son:
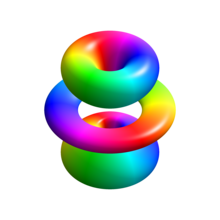
dónde:
Los números cuánticos pueden tomar los siguientes valores:
Además, estas funciones de onda están normalizadas (es decir, la integral de su módulo cuadrado es igual a 1) y ortogonales :
Las funciones de onda en el espacio de momento están relacionadas con las funciones de onda en el espacio de posición mediante una transformada de Fourier.
Las soluciones de la ecuación de Schrödinger para el hidrógeno son analíticas , dan una expresión simple para los niveles de energía del hidrógeno y, por lo tanto, las frecuencias de las líneas espectrales del hidrógeno , y reprodujeron completamente el modelo de Bohr y fueron más allá. También proporciona otros dos números cuánticos y la forma de la función de onda del electrón ("orbital") para los diversos estados mecánico-cuánticos posibles, explicando así el carácter anisotrópico de los enlaces atómicos.
La ecuación de Schrödinger también se aplica a átomos y moléculas más complicados . Cuando hay más de un electrón o núcleo, la solución no es analítica y se necesitan cálculos por computadora o se deben hacer suposiciones simplificadoras.
Dado que la ecuación de Schrödinger sólo es válida para la mecánica cuántica no relativista, las soluciones que proporciona para el átomo de hidrógeno no son del todo correctas. La ecuación de Dirac de la teoría cuántica relativista mejora estas soluciones (ver más abajo).
La solución de la ecuación de Schrödinger (ecuación de onda) para el átomo de hidrógeno utiliza el hecho de que el potencial de Coulomb producido por el núcleo es isotrópico (es radialmente simétrico en el espacio y sólo depende de la distancia al núcleo). Aunque las funciones propias de energía resultantes (los orbitales ) no son necesariamente isotrópicas en sí mismas, su dependencia de las coordenadas angulares se deriva completamente de esta isotropía del potencial subyacente: los estados propios del hamiltoniano (es decir, los estados propios de energía) se pueden elegir como simultáneos. Estados propios del operador de momento angular . Esto corresponde al hecho de que el momento angular se conserva en el movimiento orbital del electrón alrededor del núcleo. Por lo tanto, los estados propios de energía pueden clasificarse mediante dos números cuánticos de momento angular , y (ambos son números enteros). El número cuántico del momento angular determina la magnitud del momento angular. El número cuántico magnético determina la proyección del momento angular sobre el eje (elegido arbitrariamente).
Además de las expresiones matemáticas para el momento angular total y la proyección del momento angular de funciones de onda, es necesario encontrar una expresión para la dependencia radial de las funciones de onda. Sólo aquí entran los detalles del potencial de Coulomb (que conducen a los polinomios de Laguerre en ). Esto conduce a un tercer número cuántico, el número cuántico principal . El número cuántico principal del hidrógeno está relacionado con la energía total del átomo.
Tenga en cuenta que el valor máximo del número cuántico del momento angular está limitado por el número cuántico principal: sólo puede llegar hasta , es decir, .
Debido a la conservación del momento angular, estados iguales pero diferentes tienen la misma energía (esto es válido para todos los problemas de simetría rotacional ). Además, para el átomo de hidrógeno, los estados iguales pero diferentes también son degenerados (es decir, tienen la misma energía). Sin embargo, esta es una propiedad específica del hidrógeno y ya no es cierta para átomos más complicados que tienen un potencial (efectivo) que difiere de la forma (debido a la presencia de electrones internos que protegen el potencial del núcleo).
Al tener en cuenta el espín del electrón se añade un último número cuántico, la proyección del momento angular del espín del electrón a lo largo del eje -, que puede tomar dos valores. Por lo tanto, cualquier estado propio del electrón en el átomo de hidrógeno se describe completamente mediante cuatro números cuánticos. Según las reglas habituales de la mecánica cuántica, el estado real del electrón puede ser cualquier superposición de estos estados. Esto explica también por qué la elección del eje para la cuantificación direccional del vector de momento angular es irrelevante: un orbital dado y obtenido para otro eje preferido siempre puede representarse como una superposición adecuada de los distintos estados de diferentes (pero iguales ) que han sido obtenidos para .
En 1928, Paul Dirac encontró una ecuación que era totalmente compatible con la relatividad especial y (como consecuencia) convirtió la función de onda en un " espinor de Dirac " de 4 componentes que incluía componentes de espín "arriba" y "abajo", con componentes positivos y "abajo". energía "negativa" (o materia y antimateria). La solución a esta ecuación dio los siguientes resultados, más precisos que la solución de Schrödinger.
Los niveles de energía del hidrógeno, incluida la estructura fina (excluyendo el desplazamiento de Lamb y la estructura hiperfina ), vienen dados por la expresión de estructura fina de Sommerfeld : [13]
La imagen de la derecha muestra los primeros orbitales del átomo de hidrógeno (funciones propias de energía). Estas son secciones transversales de la densidad de probabilidad que están codificadas por colores (el negro representa densidad cero y el blanco representa la densidad más alta). El número cuántico del momento angular (orbital) ℓ se indica en cada columna, utilizando el código de letras espectroscópico habitual ( s significa ℓ = 0, p significa ℓ = 1, d significa ℓ = 2). El número cuántico principal (principal) n (= 1, 2, 3, ...) está marcado a la derecha de cada fila. Para todas las imágenes, el número cuántico magnético m se ha establecido en 0 y el plano de sección transversal es el plano xz ( z es el eje vertical). La densidad de probabilidad en el espacio tridimensional se obtiene girando la que se muestra aquí alrededor del eje z .
El " estado fundamental ", es decir, el estado de menor energía en el que normalmente se encuentra el electrón, es el primero, el estado 1 s ( nivel cuántico principal n = 1, ℓ = 0).
Aparecen líneas negras en todos los orbitales excepto en el primero: estos son los nodos de la función de onda, es decir, donde la densidad de probabilidad es cero. (Más precisamente, los nodos son armónicos esféricos que aparecen como resultado de resolver la ecuación de Schrödinger en coordenadas esféricas).
Los números cuánticos determinan la disposición de estos nodos. Hay: [ cita necesaria ]
Hay varios efectos importantes que la ecuación de Schrödinger ignora y que son responsables de ciertas desviaciones pequeñas pero mensurables de las líneas espectrales reales con respecto a las predichas:
Ambas características (y más) están incorporadas en la ecuación relativista de Dirac , con predicciones que se acercan aún más a la experimentación. Una vez más, la ecuación de Dirac puede resolverse analíticamente en el caso especial de un sistema de dos cuerpos, como el átomo de hidrógeno. Los estados cuánticos de la solución resultante ahora deben clasificarse por el número de momento angular total j (que surge del acoplamiento entre el espín del electrón y el momento angular orbital ). Los estados del mismo j y del mismo n todavía están degenerados. Por tanto, la solución analítica directa de la ecuación de Dirac predice 2S(1/2) y 2P(1/2) niveles de hidrógeno tienen exactamente la misma energía, lo que está en contradicción con las observaciones ( experimento de Lamb-Retherford ).
Para estos desarrollos, era esencial que la solución de la ecuación de Dirac para el átomo de hidrógeno pudiera resolverse exactamente, de modo que cualquier desviación observada experimentalmente debía tomarse en serio como una señal de fracaso de la teoría.
En el lenguaje de la mecánica matricial de Heisenberg , el átomo de hidrógeno fue resuelto por primera vez por Wolfgang Pauli [15] utilizando una simetría rotacional en cuatro dimensiones [O(4)-simetría] generada por el momento angular y el vector de Laplace-Runge-Lenz . Al extender el grupo de simetría O (4) al grupo dinámico O (4,2), todo el espectro y todas las transiciones se integraron en una única representación de grupo irreducible. [dieciséis]
En 1979, Duru y Kleinert resolvieron el átomo de hidrógeno (no relativista) por primera vez dentro de la formulación integral de caminos de la mecánica cuántica de Feynman . [17] [18] Este trabajo amplió enormemente el rango de aplicabilidad del método de Feynman .