El calendario mesoamericano de cuenta larga es un calendario no repetitivo de base 20 y base 18 utilizado por las culturas mesoamericanas precolombinas , en particular los mayas . Por esta razón, a menudo se lo conoce como el calendario maya de cuenta larga . Utilizando un recuento vigesimal modificado, el calendario de cuenta larga identifica un día contando el número de días transcurridos desde una fecha de creación mítica que corresponde al 11 de agosto de 3114 a. C. en el calendario gregoriano proléptico . [a] El calendario de cuenta larga se utilizó ampliamente en monumentos.
Los dos calendarios más utilizados en la Mesoamérica precolombina fueron el Tzolkʼin, de 260 días, y el Haabʼ, de 365 días . Los calendarios aztecas equivalentes se conocen en náhuatl como Tonalpohualli y Xiuhpohualli , respectivamente.
La combinación de una fecha Haabʼ y una Tzolkʼin identifica un día en una combinación que no se repite durante 18.980 días (52 ciclos Haabʼ de 365 días equivalen a 73 ciclos Tzolkʼin de 260 días, aproximadamente 52 años), un período conocido como la Rueda Calendárica . Para identificar días en períodos más largos que este, los mesoamericanos usaban el calendario de Cuenta Larga.
.jpg/440px-La_Mojarra_Estela_1_(Escritura_superior).jpg)
El calendario de Cuenta Larga identifica una fecha contando el número de días a partir de una fecha de inicio que generalmente se calcula como el 11 de agosto de 3114 a. C. en el calendario gregoriano proléptico o el 6 de septiembre en el calendario juliano (o -3113 en la numeración de años astronómicos). Ha habido mucho debate sobre la correlación precisa entre los calendarios occidentales y los calendarios de Cuenta Larga. La fecha del 11 de agosto se basa en la correlación GMT.
La finalización de 13 b'ak'tunes (11 de agosto de 3114 a. C.) marca la creación del mundo de los seres humanos según los mayas. En este día, el Señor del Cielo Elevado hizo que los dioses asociados colocaran tres piedras en el Cielo Acostado, el Primer Lugar de las Tres Piedras. Como el cielo todavía estaba sobre el mar primordial, estaba negro. La colocación de las tres piedras centró el cosmos, lo que permitió que el cielo se elevara y revelara el sol. [1]
En lugar de utilizar un esquema de base 10, los días de la Cuenta Larga se contaron en un esquema de base 20 modificado. En un esquema de base 20 puro, 0.0.0.1.5 es igual a 25 y 0.0.0.2.0 es igual a 40. Sin embargo, la Cuenta Larga no es de base 20 pura, ya que el segundo dígito desde la derecha (y solo ese dígito) pasa a cero cuando llega a 18. [ cita requerida ] Por lo tanto, 0.0.1.0.0 no representa 400 días, sino solo 360 días y 0.0.0.17.19 representa 359 días.
El nombre bʼakʼtun fue inventado por eruditos modernos. La cuenta larga numerada ya no se utilizaba cuando los españoles llegaron a la península de Yucatán , aunque los kʼatuns y tuns no numerados todavía se utilizaban. En su lugar, los mayas utilizaban una cuenta corta abreviada .

Las fechas de Cuenta Larga se escriben con numerales mesoamericanos, como se muestra en esta tabla. Un punto representa 1 mientras que una barra equivale a 5. El glifo de la concha se utilizó para representar el concepto del cero. El calendario de Cuenta Larga requería el uso del cero como marcador de posición y presenta uno de los primeros usos del concepto del cero en la historia .
En los monumentos mayas, la sintaxis de la Cuenta Larga es más compleja. La secuencia de fechas se da una sola vez, al principio de la inscripción y se abre con el llamado ISIG (Glifo Inicial de la Serie Introductoria) que dice tzik-a(h) habʼ [patrón del mes Haabʼ] ("reverenciado era el conteo del año con el patrón [del mes]"). [2] A continuación vienen los 5 dígitos de la Cuenta Larga, seguidos por la Rueda Calendárica (tzolkʼin y Haabʼ) y la serie suplementaria . La serie suplementaria es opcional y contiene datos lunares, por ejemplo, la edad de la luna en el día y la duración calculada de la lunación actual. [b] El texto continúa con cualquier actividad que haya ocurrido en esa fecha.
A continuación se muestra un dibujo de una inscripción maya de Cuenta Larga completa.
La inscripción de Cuenta Larga contemporánea más antigua descubierta hasta ahora se encuentra en la Estela 2 de Chiapa de Corzo , Chiapas , México, y muestra una fecha de 36 a. C., aunque la Estela 2 de Takalik Abaj , Guatemala, podría ser anterior. [3] [1] La inscripción de Cuenta Larga muy deteriorada de la Estela 2 de Takalik Abaj muestra 7 bak'tuns , seguidos de k'atuns con un coeficiente tentativo de 6, pero que también podría ser 11 o 16, lo que da el rango de fechas posibles entre 236 y 19 a. C. [c] [ cita requerida ]
Aunque la Estela 2 de Takalik Abaj sigue siendo controvertida, esta tabla la incluye, así como otros seis artefactos con las ocho inscripciones de Cuenta Larga más antiguas según el profesor de Dartmouth Vincent H. Malmström (dos de los artefactos contienen dos fechas y Malmström no incluye la Estela 2 de Takalik Abaj). [4] [5] Las interpretaciones de las inscripciones en algunos artefactos difieren. [4] [6] [7]
De los seis sitios, tres están en el borde occidental de la patria maya y tres están varios cientos de kilómetros más al oeste, lo que lleva a algunos investigadores a creer que el calendario de Cuenta Larga es anterior al maya. [11] La Estela 1 de La Mojarra, la Estatuilla de Tuxtla, la Estela C de Tres Zapotes y la Estela 2 de Chiapa están todas inscritas en un estilo epiolmeca , no maya. [12] La Estela 2 de El Baúl, por otro lado, fue creada en el estilo Izapa .
El primer artefacto inequívocamente maya es la Estela 29 de Tikal , con fecha de Cuenta Larga de 292 d.C. (8.12.14.8.15), más de 300 años después de la Estela 2 de Chiapa de Corzo. [13]
Más recientemente, con el descubrimiento en Guatemala del texto en bloque de piedra de San Bartolo (sitio maya) ( c. 300 a. C.), [14] se ha argumentado que este texto celebra la celebración del fin de un período de tiempo próximo. Es posible que se haya proyectado que este período de tiempo terminara en algún momento entre 7.3.0.0.0 (295 a. C.) y 7.5.0.0.0 (256 a. C.). [15] Además de ser el texto jeroglífico maya más antiguo descubierto hasta ahora, podría decirse que este sería la evidencia más temprana hasta la fecha de notación de Cuenta Larga en Mesoamérica.

Los calendarios maya y occidental están correlacionados mediante el uso de un número de día juliano (JDN) de la fecha de inicio de la creación actual: 13.0.0.0.0, 4 Ajaw , 8 Kumkʼu. [d] Esto se conoce como una "constante de correlación". La constante de correlación generalmente aceptada es la Thompson 2 modificada, " Goodman –Martinez– Thompson ", o correlación GMT de 584.283 días. Usando la correlación GMT, la creación actual comenzó el 6 de septiembre de −3113 ( juliano astronómico) - 11 de agosto de 3114 a. C. en el calendario gregoriano proléptico . El estudio de la correlación del calendario maya y occidental se conoce como la cuestión de la correlación. [16] [17] [18] [19] [20] La correlación GMT también se llama correlación 11.16 .
En Breaking the Maya Code , Michael D. Coe escribe: "A pesar de los océanos de tinta que se han vertido sobre el tema, ahora no existe la más mínima posibilidad de que estos tres eruditos (que se confunden con GMT cuando se habla de la correlación) no estuvieran en lo cierto...". [21] La evidencia de la correlación GMT es histórica, astronómica y arqueológica:
Histórico : Las fechas de la Rueda Calendárica con una fecha juliana correspondiente se registran en la Relación de las cosas de Yucatán de Diego de Landa (escrita alrededor de 1566), la Crónica de Oxcutzkab y los libros de Chilam Balam . De Landa registra una fecha que es una terminación Tun en la Cuenta Corta . Oxkutzcab contiene 12 terminaciones Tun. Bricker y Bricker encuentran que solo la correlación GMT es consistente con estas fechas. [22] El Libro de Chilam Balam de Chumayel [23] contiene la única referencia colonial a fechas clásicas de cuenta larga. La fecha del calendario juliano de 11.16.0.0.0 (2 de noviembre de 1539) confirma la correlación GMT. [24]
Los Anales de los Cakchiqueles contienen numerosas fechas Tzolkʼin correlacionadas con fechas europeas. Estas confirman la correlación GMT. [25] Weeks, Sachse y Prager transcribieron tres calendarios adivinatorios de las tierras altas de Guatemala. Encontraron que el calendario de 1772 confirma la correlación GMT. [26] La caída de la ciudad capital del Imperio Azteca, Tenochtitlan , ocurrió el 13 de agosto de 1521. [27] Varios cronistas diferentes escribieron que la fecha Tzolkʼin ( Tonalpohualli ) del evento fue 1 Serpiente. [28]
Los estudiosos de la posconquista, como Sahagún y Durán, registraron las fechas del Tonalpohualli con una fecha del calendario. Muchas comunidades indígenas de los estados mexicanos de Veracruz, Oaxaca y Chiapas [29] y de Guatemala, principalmente las que hablan las lenguas mayas ixil, mam, pokomchí y quiché, conservan el Tzolkʼin y en muchos casos el Haabʼ. [30] Todos estos son consistentes con la correlación GMT. Munro Edmonsen estudió 60 calendarios mesoamericanos, 20 de los cuales tienen correlaciones conocidas con los calendarios europeos, y encontró una notable consistencia entre ellos y que sólo la correlación GMT se ajusta a la evidencia histórica, etnográfica y astronómica. [31]
Astronómico : Cualquier correlación correcta debe coincidir con el contenido astronómico de las inscripciones clásicas. La correlación GMT hace un excelente trabajo de coincidencia de datos lunares en la serie suplementaria . [32] Por ejemplo: Una inscripción en el Templo del Sol en Palenque registra que en la Cuenta Larga 9.16.4.10.8 se completaron 26 días en una lunación de 30 días. [33] Esta Cuenta Larga es también la fecha de entrada para la tabla de eclipses del Códice de Dresde . [34] [e]
Utilizando el tercer método, el sistema de Palenque, [36] la luna nueva habría sido la primera tarde en la que uno podía mirar hacia el oeste después del atardecer y ver la delgada luna creciente. Dada nuestra capacidad moderna de saber exactamente dónde mirar, cuando la luna creciente está favorablemente ubicada, desde un sitio excelente, en raras ocasiones, utilizando binoculares o un telescopio, los observadores pueden ver y fotografiar la luna creciente menos de un día después de la conjunción. Generalmente, la mayoría de los observadores no pueden ver la luna nueva a simple vista hasta la primera tarde cuando el día de la fase lunar es al menos 1.5. [37] [38] [39] [40] [41] [42] Si uno asume que la luna nueva es el primer día en el que el día de la fase lunar es al menos 1.5 a las seis de la tarde en la zona horaria UTC−6 (la zona horaria del área maya), la correlación GMT coincidirá exactamente con muchas inscripciones lunares. En este ejemplo, el día de la fase lunar fue 27,7 (26 días contando desde cero) a las 6 p. m. después de una conjunción a la 1:25 a. m. del 10 de octubre de 755 y una Luna nueva cuando el día de la fase lunar fue 1,7 a las 6 p. m. del 11 de octubre de 755 (calendario juliano). Esto funciona bien para muchas inscripciones lunares, pero no para todas.
Los astrónomos modernos se refieren a la conjunción del Sol y la Luna (el momento en que el Sol y la Luna tienen la misma longitud eclíptica) como la luna nueva. Pero la astronomía mesoamericana era observacional , no teórica. Los pueblos de Mesoamérica no conocían la naturaleza copernicana del sistema solar; no tenían una comprensión teórica de la naturaleza orbital de los cuerpos celestes. Algunos autores analizan las inscripciones lunares basándose en esta comprensión moderna de los movimientos de la Luna, pero no hay evidencia de que los mesoamericanos la compartieran.
El primer método parece haber sido utilizado para otras inscripciones como la estela E de Quirgua (9.17.0.0.0). Según el tercer método, esa estela debería mostrar una edad lunar de 26 días, pero en realidad registra una luna nueva. [43] Utilizando la correlación GMT a las seis de la mañana en la zona horaria UTC−6, esto sería 2,25 días antes de la conjunción, por lo que podría registrar el primer día en el que no se podía ver la luna menguante.
Fuls [44] analizó estas inscripciones y encontró evidencia sólida del sistema Palenque y la correlación GMT; sin embargo, advirtió: "El análisis de la serie lunar muestra que se utilizaron al menos dos métodos y fórmulas diferentes para calcular la edad y la posición de la luna en el ciclo de seis meses...", lo que da estaciones de eclipse cuando la Luna está cerca de su nodo ascendente o descendente y es probable que ocurra un eclipse . Las fechas convertidas utilizando la correlación GMT concuerdan estrechamente con las tablas de eclipse del Códice de Dresde. [45] El Códice de Dresde contiene una tabla de Venus que registra las salidas helíacas de Venus. Usando la correlación GMT, estas concuerdan estrechamente con los cálculos astronómicos modernos. [46]
Arqueológico : Varios elementos que pueden asociarse con fechas específicas de Cuenta Larga han sido datados con isótopos . En 1959, la Universidad de Pensilvania fechó con carbono muestras de diez dinteles de madera de Tikal . [47] Estos fueron tallados con una fecha equivalente a 741 d. C., utilizando la correlación GMT. La fecha de carbono promedio fue de 746 ± 34 años. Recientemente, uno de estos, el Dintel 3 del Templo I, fue analizado nuevamente utilizando métodos más precisos y se encontró que concordaba estrechamente con la correlación GMT. [48]
Si una correlación propuesta sólo tiene que concordar con una de estas líneas de evidencia, podrían existir muchas otras posibilidades. Los astrónomos han propuesto muchas correlaciones, por ejemplo: Lounsbury , [49] Fuls, et al. , [50] Böhm y Böhm [51] [52] y Stock. [53]
Hoy, 24 de octubre de 2024 ( UTC ), en la cuenta larga es 13.0.12.0.5 (utilizando la correlación GMT).
Según el Popol Vuh , un libro que recopila detalles de los relatos de la creación conocidos por los mayas quiché de las tierras altas de la era colonial, la humanidad vive en el cuarto mundo. [54] El Popol Vuh describe las primeras tres creaciones que los dioses no lograron hacer y la creación del cuarto mundo exitoso donde fueron colocados los hombres. En la Cuenta Larga maya, la creación anterior terminó al final de un decimotercer b'ak'tun.
La creación anterior finalizó en una Cuenta Larga de 12.19.19.17.19. Otro 12.19.19.17.19 ocurrió el 20 de diciembre de 2012 (calendario gregoriano), seguido por el inicio del 14.º bʼakʼtun, 13.0.0.0.0, el 21 de diciembre de 2012. [f] Solo hay dos referencias al 13.º bʼakʼtun de la creación actual en el corpus maya fragmentario: el Monumento 6 de Tortuguero , parte de la inscripción de un gobernante y la recientemente descubierta Escalinata Jeroglífica La Corona 2, Bloque V. [56]
En ocasiones, las inscripciones mayas hacen referencia a eventos futuros o conmemoraciones predichas que ocurrirían en fechas posteriores a 2012 (es decir, posteriores a la finalización del 13.º b'ak'tun de la era actual). La mayoría de ellas se presentan en forma de "fechas de distancia", en las que se da una fecha de Cuenta Larga, junto con un Número de Distancia que se debe agregar a la fecha de Cuenta Larga para llegar a esta fecha futura.
Por ejemplo, en el panel oeste del Templo de las Inscripciones en Palenque , una sección del texto se proyecta hacia el futuro hasta el 80.° aniversario de la Rueda Calendárica (RC) de la ascensión al trono del famoso gobernante de Palenque Kʼinich Janaabʼ Pakal (la ascensión al trono de Pakal ocurrió en una fecha de la Rueda Calendárica 5 Lamat 1 Mol, en la Cuenta Larga 9.9.2.4.8 equivalente al 27 de julio de 615 d. C. en el calendario gregoriano proléptico ). [g] Lo hace comenzando con la fecha de nacimiento de Pakal 9.8.9.13.0 8 Ajaw 13 Pop (24 de marzo de 603 d. C. gregoriano ) y añadiéndole el Número de Distancia 10.11.10.5.8. [57]
Este cálculo llega a la 80.ª Rueda Calendárica desde su ascenso al trono, un día que también tiene una fecha CR de 5 Lamat 1 Mol , pero que se encuentra a más de 4.000 años en el futuro desde la época de Pakal: el día 21 de octubre del año 4772. La inscripción señala [ cita requerida ] que este día caería ocho días después de la finalización del primer piktun (desde la creación o fecha cero del sistema de Cuenta Larga), donde el piktun es el siguiente orden más alto por encima del bʼakʼtun en la Cuenta Larga. Si la fecha de finalización de ese piktun —13 de octubre de 4772— se escribiera en notación de Cuenta Larga, podría representarse como 1.0.0.0.0.0. La fecha del 80.º aniversario de la CR, ocho días después, sería 1.0.0.0.0.8 5 Lamat 1 Mol. [57] [58]
A pesar de la publicidad generada por la fecha de 2012, Susan Milbrath, curadora de Arte y Arqueología Latinoamericana en el Museo de Historia Natural de Florida , declaró que "no tenemos registro ni conocimiento de que [los mayas] pensaran que el mundo llegaría a su fin" en 2012. [59] USA Today escribe : " Para los antiguos mayas, era una gran celebración llegar al final de todo un ciclo", dice Sandra Noble, directora ejecutiva de la Fundación para el Avance de los Estudios Mesoamericanos en Crystal River, Florida . Presentar el 21 de diciembre de 2012 como un evento del fin del mundo o un momento de cambio cósmico, dice, es "una invención completa y una oportunidad para que mucha gente saque provecho " . [59] " Habrá otro ciclo", dice E. Wyllys Andrews V, director del Instituto de Investigación Mesoamericana (MARI) de la Universidad de Tulane . "Sabemos que los mayas pensaban que había uno antes de este, y eso implica que se sentían cómodos con la idea de otro después de este". [60]
Es importante conocer la diferencia entre los calendarios juliano y gregoriano al calcular una fecha del calendario occidental a partir de una fecha de Cuenta Larga. [h]
Utilizando como ejemplo la fecha de Cuenta Larga de 9.10.11.17.0 (fecha de Cuenta Larga mencionada en la Tabla del Palacio de Palenque), primero calcule el número de días que han transcurrido desde la fecha cero (11 de agosto de 3114 a. C.; correlación GMT, en el calendario gregoriano proléptico , 6 de septiembre de −3113 astronómico juliano ).
Luego agregue la correlación GMT al número total de días.
Este número es un día juliano .
Para convertir un día juliano en una fecha del calendario gregoriano proléptico : [61]
A este número, reste el número de día juliano más pequeño más cercano (en la tabla a continuación), en este caso 1.940.206, que corresponde al año 600 d.C.
A continuación, divide este número por 365 días (año vago).
El resto son 44,86849 años, es decir, 44 años y 317 días. La fecha del año completo es 644 d. C. Ahora calcule el número de mes y día, teniendo en cuenta los días bisiestos durante los 44 años. En el calendario gregoriano, cada cuarto año es bisiesto con la excepción de los siglos que no son divisibles por 400 (por ejemplo, 100, 200, 300). Cuando el año es divisible por 400 (por ejemplo, 400, 800, etc.), no agregue un día adicional. El año calculado es 644 d. C. El número de días bisiestos, teniendo en cuenta que el año 600 no es bisiesto, es 10. Restando eso de los 317 días restantes es 307; en otras palabras, el día 307 del año 644 d.C., que es el 3 de noviembre. Para resumir: la fecha de Cuenta Larga 9.10.11.17.0 corresponde al 3 de noviembre de 644 d.C., en el calendario gregoriano proléptico .
Para convertir un día juliano en una fecha astronómica juliana/gregoriana ( calendario juliano proléptico anterior al 46 a. C.):
Utilice un algoritmo astronómico como el Método de Meeus [62] para convertir el día juliano en una fecha juliana/gregoriana con datación astronómica de años negativos: [i]
En este ejemplo:
Entrada: día juliano J J = J + 0,5 // 1.956.583,5 Z = parte entera de J // 1.956.583 F = parte fraccionaria de J // 0,5si Z < 2.299.161 entonces // Julian? A = Z else alpha = floor(( Z - 1.867.216,25) / 36.524,25) // 15 A = Z + 1 + alpha - floor( alpha / 4,0) // 2.436.129 // La operación floor redondea un número decimal hacia abajo hasta el siguiente entero más bajo. // Por ejemplo, floor(1,5) = 1 y floor(−1,5) = -2 end ifB = A + 1524 // 1.958.107 C = piso(( B - 122,1) / 365,25) // 5.360 D = piso(365,25 × C ) // 1.957.740 E = piso(( B - D ) / 30,6001) // 11 día = B - D - piso(30,6001 × E ) + F // 31,5si E < 14 entonces mes = E - 1 // 10 de lo contrario mes = E - 13 fin sisi mes > 2 entonces año = C - 4716 // 644 de lo contrario año = C - 4715 fin siretorno ( año , mes , día )
En este ejemplo la fecha juliana es el mediodía del 31 de octubre de 644. El método de Meeus no es válido para números de años negativos (astronómicos), por lo que se debe utilizar otro método como el método de Peter Baum [63] .
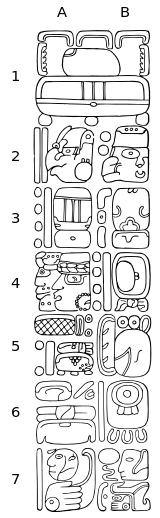
Una fecha completa de Cuenta Larga no solo incluye los cinco dígitos de la Cuenta Larga, sino también los dos caracteres del Tzolkʼin y los dos caracteres del Haabʼ. Por lo tanto, la Cuenta Larga de cinco dígitos se puede confirmar con los otros cuatro caracteres (la "fecha circular del calendario").
Tomando como ejemplo la fecha de la Rueda Calendárica 9.12.2.0.16 (Cuenta Larga) 5 Kibʼ (Tzolkʼin) 14 Yaxkʼin (Haabʼ). Se puede comprobar si esta fecha es correcta mediante el siguiente cálculo.
Quizás sea más fácil averiguar cuántos días hay desde 4 Ajaw 8 Kumkʼu y mostrar cómo se deriva la fecha 5 Kibʼ 14 Yaxkʼin.
La fecha del Tzolkʼin se cuenta hacia adelante a partir del 4 de Ajaw. Para calcular la parte numérica de la fecha del Tzolkʼin, se suma 4 al número total de días que indica la fecha y luego se divide el número total de días por 13.
Esto significa que se han completado 106.395 ciclos completos de 13 días y la porción numérica de la fecha del Tzolkʼin es 5.
Para calcular el día, divida el número total de días en la cuenta larga por 20, ya que hay veinte nombres de días.
Esto significa que se deben contar 16 nombres de días a partir de Ajaw. Esto da Kibʼ. Por lo tanto, la fecha del Tzolkʼin es 5 Kibʼ.
La fecha del Haab' 8 Kumk'u es el noveno día del decimoctavo mes. Faltan 17 días para el comienzo del año siguiente.
Reste 17 días del total para saber cuántos años Haabʼ completos contiene.
por 365
Por lo tanto, han pasado 3.789 Haabʼ completos y el resto 134 es el día 135 del nuevo Haabʼ, ya que un resto de 0 indicaría el primer día.
Encuentra en qué mes se encuentra el día. Dividiendo el resto 134 por 20, se obtienen seis meses completos y un resto de 14, lo que indica el día 15. Por lo tanto, la fecha en el Haabʼ se encuentra en el séptimo mes, que es Yaxkʼin. El decimoquinto día de Yaxkʼin es 14, por lo tanto, la fecha del Haabʼ es 14 Yaxkʼin.
Por lo tanto, se confirma la fecha de la cuenta larga 9.12.2.0.16 5 Kibʼ 14 Yaxkʼin.
Además del b'ak'tun, hay cuatro períodos de orden superior que rara vez se utilizan: piktun , kalabtun , k'inchiltun y alautun . Todas estas palabras son invenciones de los mayistas. Cada una consta de 20 de las unidades menores. [64] [65] [j] [66]
Muchas inscripciones dan la fecha de la creación actual como un gran número de 13 que preceden a 13.0.0.0.0 4 Ahau 8 Kumkʼu. Por ejemplo, un monumento del Clásico Tardío de Cobá , Estela 1. La fecha de creación se expresa como 13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.0.0.0.0, donde las unidades son 13 en los diecinueve lugares más grandes que el bʼakʼtun. [67] [68] [69] [70] Algunos autores piensan que los 13 eran un símbolo de una finalización y no representaban un número real. [71]
La mayoría de las inscripciones que utilizan estos métodos se presentan en forma de fechas de distancia y cálculos largos: proporcionan una fecha base, un número de distancia que se suma o se resta y el cálculo largo resultante.
El primer ejemplo que se muestra a continuación es de Schele (1987). El segundo es de Stuart (2005, págs. 60, 77) [72].
Templo de la Cruz de Palenque, tablilla, Schele (1987 p.)
12.19.13.4.0 8 Ajaw 18 Tzek en la era anterior
6.14.0 Número de distancia que vincula a la "fecha de la era"
13.0.0.0.0 4 Ajaw 8 Kumkʼu
Templo XIX de Palenque, Panel Sur G2-H6 Stuart (2005 pp. 60, 77)
12.10.1.13.2 9 Ikʼ 5 Mol (asentamiento de GI en la era anterior)
2.8.3.8.0
1.18.5.3.2 9 Ikʼ 15 Keh (renacimiento de GI, esta fecha también aparece en el Templo de la Cruz)
La tablilla de las inscripciones contiene esta inscripción: [71]
9.8.9.13.0 8 Ajaw 13 Pop
10.11.10.5.8
1.0.0.0.0.8
El códice de Dresde contiene otro método para escribir los números de distancia. Se trata de los números de anillo. Las fechas específicas dentro del códice de Dresde se dan a menudo mediante cálculos que implican números de anillo. Förstemann [73] los identificó, pero Wilson (1924) : 24–25 aclaró más tarde la forma en que funcionan. Los números de anillo son intervalos de días entre la fecha de la base de la era 4 Ajaw 8 Kumkʼu y una fecha de la base de anillo anterior, donde el marcador de posición para el número de días en el intervalo está rodeado por una imagen de una banda roja atada. A esta fecha de la base de anillo anterior se suma otro conteo de días hacia adelante, al que Thompson [74] se refiere como una ronda larga, que conduce a una fecha final dentro de la cuenta larga que se da como una fecha de entrada para ser utilizada dentro de una tabla específica en el códice. [75]
Número de anillo (12) 12.12.17.3.1 13 Imix 9 Wo (7.2.14.19 antes de (13) 13.0.0.0.0)
número de distancia (0) 10.13.13.3.2
Cuenta larga 10.6.10.6.3 13 Akʼbal 1 Kankʼin
Número de anillo (parte del DN anterior a la fecha de la era) 7.2.14.19
Agregue el número de anillo a la fecha del número de anillo para llegar a 13.0.0.0.0
Thompson [76] contiene una tabla de cálculos largos típicos según Satterwaite. [72]
Los "Números de la Serpiente" en el códice de Dresde, páginas 61-69, son una tabla de fechas que utiliza una fecha base de 1.18.1.8.0.16 en la era anterior (5.482.096 días). [77] [78] [79]
El cambio paralelo *oo Ͼ *uu Ͼ *u en Chʼolan está atestiguado indirectamente en el uso del logograma T548 TUN/HABʼ con el Glifo Introductorio de la Serie Inicial en la Estela 2 de Takalik Abaj (236–19 a. C.; Justeson y Mathews 1983; MoraMarín 2001:253).
Si se aceptan las 12 terminaciones de tun en la Crónica de Oxkutzcab como referencias a los 12 años consecutivos y si las fechas del calendario redondo (excepto la que contiene el mes de Ceh) son correctas al traducirlas a un calendario común, la correlación "11.16" es la única posible.
con correcciones al 10 de agosto de 2009
En ocasiones, los mayas también registraron intervalos de tiempo incluso mayores que 13 B'ak'tunes, como un Piktun, compuesto de 20 B'ak'tunes. Esto es relevante para el debate actual sobre la serie de la serpiente.