Conjetura de Goldbach

Números enteros pares como sumas de dos primos

La conjetura de Goldbach es uno de los problemas sin resolver más antiguos y conocidos de la teoría de números y de toda la matemática . Establece que todo número natural par mayor que 2 es la suma de dos números primos .

Se ha demostrado que la conjetura es válida para todos los números enteros menores que4 × 10 ¹⁸ , pero sigue sin demostrarse a pesar del considerable esfuerzo.

Historia

Orígenes

El 7 de junio de 1742, el matemático prusiano Christian Goldbach escribió una carta a Leonhard Euler (carta XLIII), ^[2] en la que proponía la siguiente conjetura:

dass jede Zahl, welche aus zweyen numeris primis zusammengesetzt ist, ein aggregatum so vieler numerorum primorum sey, als man will (die unitatem mit dazu gerechnet), bis auf die congeriem omnium unitatum
Todo número entero que pueda escribirse como la suma de dos números primos puede También puede escribirse como la suma de tantos números primos como se desee, hasta que todos los términos sean unidades.

Goldbach seguía la convención, hoy abandonada, de considerar al 1 como un número primo , ^[3] de modo que una suma de unidades sería una suma de primos. Luego propuso una segunda conjetura en el margen de su carta, que implica la primera: ^[4]

... eine jede Zahl, die grösser ist als 2, ein aggregatum trium numerorum primorum sey.
Todo número entero mayor que 2 se puede escribir como la suma de tres números primos.

Euler respondió en una carta fechada el 30 de junio de 1742 ^[5] y le recordó a Goldbach una conversación anterior que habían tenido (" ... así que Ew vormals mit mir communicirt haben... "), en la que Goldbach había comentado que la primera de esas dos conjeturas se seguiría de la afirmación

Todo número entero par positivo puede escribirse como la suma de dos primos.

De hecho, esto es equivalente a su segunda conjetura marginal. En la carta fechada el 30 de junio de 1742, Euler afirmó: ^{[6] [7]}

Dass... ein jeder numerus par eine summa duorum primorum sey, halte ich für ein ganz gewisses teorema, ungeachtet ich dasselbe nicht demonstriren kann.
Que... todo número par es una suma de dos primos, lo considero un teorema completamente seguro, aunque no puedo demostrarlo.

Resultados parciales

La conjetura fuerte de Goldbach es mucho más difícil que la conjetura débil de Goldbach , que dice que todo entero (equivalentemente, todo entero impar) mayor que 5 es la suma de tres primos. Utilizando el método de Vinogradov , Nikolai Chudakov , ^[8] Johannes van der Corput , ^[9] y Theodor Estermann ^[10] demostraron (1937-1938) que casi todos los números pares pueden escribirse como la suma de dos primos (en el sentido de que la fracción de números pares hasta algún N que puede escribirse así tiende a 1 a medida que N aumenta). En 1930, Lev Schnirelmann demostró que cualquier número natural mayor que 1 puede escribirse como la suma de no más de C números primos, donde C es una constante efectivamente computable; véase densidad de Schnirelmann . ^{[11] [12]} La constante de Schnirelmann es el número C más bajo con esta propiedad. El propio Schnirelmann obtuvo C <800 000 . Este resultado fue mejorado posteriormente por muchos autores, como Olivier Ramaré , quien en 1995 demostró que todo número par n ≥ 4 es de hecho la suma de como máximo 6 primos. El resultado más conocido actualmente proviene de la demostración de la conjetura débil de Goldbach de Harald Helfgott , ^[13] que implica directamente que todo número par n ≥ 4 es la suma de como máximo 4 primos. ^{[14] [15]}

En 1924, Hardy y Littlewood demostraron, bajo el supuesto de la hipótesis generalizada de Riemann , que el número de números pares hasta X que violan la conjetura de Goldbach es mucho menor que X ^{1 ⁄ 2 + c} para c pequeño . ^[16]

En 1948, utilizando métodos de teoría de tamices , Alfréd Rényi demostró que todo número par suficientemente grande puede escribirse como la suma de un primo y un casi primo con un máximo de K factores. ^[17] Chen Jingrun demostró en 1973 utilizando la teoría de tamices que todo número par suficientemente grande puede escribirse como la suma de dos primos o de un primo y un semiprimo (el producto de dos primos). ^[18] Véase el teorema de Chen para más información.

En 1975, Hugh Lowell Montgomery y Bob Vaughan demostraron que "la mayoría" de los números pares se pueden expresar como la suma de dos primos. Más precisamente, demostraron que existen constantes positivas c y C tales que para todos los números suficientemente grandes N , todo número par menor que N es la suma de dos primos, con como máximo CN ^{1 − c} excepciones. En particular, el conjunto de números enteros pares que no son la suma de dos primos tiene densidad cero.

En 1951, Yuri Linnik demostró la existencia de una constante K tal que todo número par suficientemente grande es la suma de dos primos y como máximo K potencias de 2. János Pintz e Imre Ruzsa descubrieron en 2020 que K = 8 funciona. ^[19] Suponiendo la hipótesis de Riemann generalizada , K = 7 también funciona, como lo demostraron Roger Heath-Brown y Jan-Christoph Schlage-Puchta en 2002. ^[20]

En 2013, Harald Helfgott presentó una prueba de la conjetura débil a la serie Annals of Mathematics Studies . Aunque el artículo fue aceptado, Helfgott decidió llevar a cabo las modificaciones importantes sugeridas por el árbitro. A pesar de varias revisiones, la prueba de Helfgott aún no ha aparecido en una publicación revisada por pares. ^{[21] [22] [23]} La conjetura débil está implícita en la conjetura fuerte, como si n − 3 fuera una suma de dos primos, entonces n es una suma de tres primos. Sin embargo, la implicación inversa y, por lo tanto, la conjetura fuerte de Goldbach permanecerían sin demostrar si la prueba de Helfgott es correcta.

Resultados computacionales

Para valores pequeños de n , la conjetura fuerte de Goldbach (y, por lo tanto, la conjetura débil de Goldbach) se puede verificar directamente. Por ejemplo, en 1938, Nils Pipping verificó laboriosamente la conjetura hasta n =100 000 . ^[24] Con la llegada de las computadoras, se han comprobado muchos más valores de n ; T. Oliveira e Silva realizó una búsqueda computacional distribuida que verificó la conjetura para n ≤4 × 10 ¹⁸ (y verificado dos veces hasta4 × 10 ¹⁷ ) a partir de 2013. Un registro de esta búsqueda es que3 325 581 707 333 960 528 es el número más pequeño que no se puede escribir como suma de dos primos donde uno es menor que 9781. ^[25]

Cully-Hugill y Dudek prueban ^[26] un resultado (parcial y condicional) sobre la hipótesis de Riemann: existe una suma de dos primos impares en el intervalo (x, x + 9696 log^2 x] para todo x ≥ 2.

En la cultura popular

La conjetura de Goldbach ( en chino :哥德巴赫猜想) es el título de la biografía del matemático y teórico de números chino Chen Jingrun , escrita por Xu Chi .

La conjetura es un punto central en la trama de la novela de 1992 La conjetura del tío Petros y Goldbach del autor griego Apostolos Doxiadis , en el cuento " Sesenta millones de billones de combinaciones " de Isaac Asimov y también en la novela de misterio de 2008 No One You Know de Michelle Richmond . ^[27]

La conjetura de Goldbach es parte de la trama de la película española de 2007 La habitación de Fermat .

La conjetura de Goldbach aparece como el tema principal de investigación del personaje de Marguerite, interpretado por la actriz Ella Rumpf , en la película franco-suiza de 2023 El teorema de Marguerite . ^[28]

Declaración formal

Cada una de las tres conjeturas tiene un análogo natural en términos de la definición moderna de primo, según la cual se excluye el 1. Una versión moderna de la primera conjetura es:

Todo número entero que pueda escribirse como suma de dos primos también puede escribirse como suma de tantos primos como se desee, hasta que todos los términos sean dos (si el número entero es par) o un término sea tres y todos los demás términos sean dos (si el número entero es impar).

Una versión moderna de la conjetura marginal es:

Todo número entero mayor que 5 puede escribirse como la suma de tres primos.

Y una versión moderna de la antigua conjetura de Goldbach que Euler le recordó es:

Todo número entero par mayor que 2 puede escribirse como la suma de dos primos.

Estas versiones modernas podrían no ser completamente equivalentes a los enunciados originales correspondientes. Por ejemplo, si hubiera un entero par N = p + 1 mayor que 4, para p un primo, que no pudiera expresarse como la suma de dos primos en el sentido moderno, entonces sería un contraejemplo de la versión moderna de la tercera conjetura (sin ser un contraejemplo de la versión original). La versión moderna es, por lo tanto, probablemente más fuerte (pero para confirmarlo, habría que demostrar que la primera versión, aplicada libremente a cualquier entero par positivo n , no podría descartar de ninguna manera la existencia de un contraejemplo específico N ). En cualquier caso, los enunciados modernos tienen las mismas relaciones entre sí que los enunciados antiguos. Es decir, el segundo y el tercer enunciados modernos son equivalentes, y cualquiera de ellos implica el primer enunciado moderno.

La tercera afirmación moderna (equivalente a la segunda) es la forma en que se suele expresar la conjetura en la actualidad. También se la conoce como conjetura de Goldbach " fuerte ", "par" o "binaria". Una forma más débil de la segunda afirmación moderna, conocida como " conjetura débil de Goldbach ", "conjetura de Goldbach impar" o "conjetura de Goldbach ternaria", afirma que

Todo número entero impar mayor que 7 puede escribirse como la suma de tres primos impares.

Justificación heurística

Sumas de dos primos en las intersecciones de tres rectas

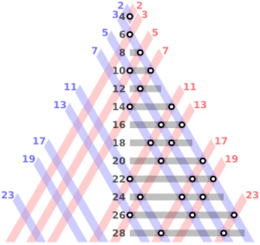
Las consideraciones estadísticas que se centran en la distribución probabilística de los números primos presentan evidencia informal a favor de la conjetura (tanto en la forma débil como en la fuerte) para números enteros suficientemente grandes : cuanto mayor sea el número entero, más formas disponibles hay para representar ese número como la suma de otros dos o tres números, y más "probable" es que al menos una de estas representaciones consista enteramente en primos.

Número de formas de escribir un número par n como suma de dos primos (secuencia A002375 en la OEIS )

Una versión muy cruda del argumento probabilístico heurístico (para la forma fuerte de la conjetura de Goldbach) es la siguiente. El teorema de los números primos afirma que un entero m seleccionado al azar tiene aproximadamente una1/En m⁠ probabilidad de ser primo. Por lo tanto, si n es un entero par grande y m es un número entre 3 y ⁠norte/2⁠ , entonces se podría esperar que la probabilidad de que m y n − m sean primos simultáneamente sea ⁠1/en m en( n − m )⁠ . Si se sigue esta heurística, se podría esperar que el número total de formas de escribir un entero par grande n como la suma de dos primos impares sea aproximadamente

${\displaystyle \sum _{m=3}^{\frac {n}{2}}{\frac {1}{\ln m}}{\frac {1}{\ln(n-m)}}\approx {\frac {n}{2(\ln n)^{2}}}.}$

Como ln n ≪ √ n , esta cantidad tiende a infinito a medida que n aumenta, y uno esperaría que cada entero par grande no solo tenga una representación como suma de dos primos, sino, de hecho, muchas representaciones de ese tipo.

Este argumento heurístico es en realidad algo inexacto porque supone que los eventos de que m y n − m sean primos son estadísticamente independientes entre sí. Por ejemplo, si m es impar, entonces n − m también es impar, y si m es par, entonces n − m es par, una relación no trivial porque, además del número 2, solo los números impares pueden ser primos. De manera similar, si n es divisible por 3, y m ya era un primo distinto de 3, entonces n − m también sería coprimo de 3 y, por lo tanto, sería ligeramente más probable que fuera primo que un número general. Al continuar este tipo de análisis con más cuidado, GH Hardy y John Edensor Littlewood en 1923 conjeturaron (como parte de su conjetura de tupla prima de Hardy-Littlewood ) que para cualquier c fijo ≥ 2 , el número de representaciones de un entero grande n como la suma de c primos n = p ₁ + ⋯ + p _c con p ₁ ≤ ⋯ ≤ p _c debería ser asintóticamente igual a

${\displaystyle \left(\prod _{p}{\frac {p\gamma _{c,p}(n)}{(p-1)^{c}}}\right)\int _{2\leq x_{1}\leq \cdots \leq x_{c}:x_{1}+\cdots +x_{c}=n}{\frac {dx_{1}\cdots dx_{c-1}}{\ln x_{1}\cdots \ln x_{c}}},}$

donde el producto es sobre todos los primos p , y γ _{c , p} ( n ) es el número de soluciones de la ecuación n = q ₁ + ⋯ + q _c mod p en aritmética modular , sujeta a las restricciones q ₁ , …, q _c ≠ 0 mod p . Se ha demostrado rigurosamente que esta fórmula es asintóticamente válida para c ≥ 3 a partir del trabajo de Ivan Matveevich Vinogradov , pero sigue siendo solo una conjetura cuando c = 2 . ^{[ cita requerida ]} En el último caso, la fórmula anterior se simplifica a 0 cuando n es impar, y a

${\displaystyle 2\Pi _{2}\left(\prod _{p\mid n;p\geq 3}{\frac {p-1}{p-2}}\right)\int _{2}^{n}{\frac {dx}{(\ln x)^{2}}}\approx 2\Pi _{2}\left(\prod _{p\mid n;p\geq 3}{\frac {p-1}{p-2}}\right){\frac {n}{(\ln n)^{2}}}}$

cuando n es par, donde Π ₂ es la constante de primos gemelos de Hardy-Littlewood

${\displaystyle \Pi _{2}:=\prod _{p\;{\rm {prime}}\geq 3}\left(1-{\frac {1}{(p-1)^{2}}}\right)\approx 0.66016\,18158\,46869\,57392\,78121\,10014\dots }$

A veces se la conoce como conjetura de Goldbach extendida . La conjetura fuerte de Goldbach es, de hecho, muy similar a la conjetura de los primos gemelos , y se cree que ambas conjeturas tienen una dificultad aproximadamente comparable.

Cometa Goldbach; los puntos rojo, azul y verde corresponden respectivamente a los valores 0, 1 y 2 módulo 3 del número.

La función de partición de Goldbach es la función que asocia a cada número entero par el número de formas en que puede descomponerse en una suma de dos primos. Su gráfica se parece a un cometa y por eso se le llama cometa de Goldbach . ^[29]

El cometa Goldbach sugiere límites superiores e inferiores estrictos para el número de representaciones de un número par como suma de dos primos, y también que el número de estas representaciones depende en gran medida del valor módulo 3 del número.

Problemas relacionados

Aunque la conjetura de Goldbach implica que todo entero positivo mayor que uno puede escribirse como una suma de tres primos como máximo, no siempre es posible hallar dicha suma utilizando un algoritmo voraz que utilice el primo más grande posible en cada paso. La secuencia de Pillai rastrea los números que requieren la mayor cantidad de primos en sus representaciones voraces. ^[30]

Existen problemas similares a la conjetura de Goldbach en los que los primos son reemplazados por otros conjuntos particulares de números, como los cuadrados:

• Lagrange demostró que todo entero positivo es la suma de cuatro cuadrados . Véase el problema de Waring y el problema relacionado de Waring-Goldbach sobre sumas de potencias de números primos.
• Hardy y Littlewood enumeraron como su Conjetura I: "Todo número impar grande ( n > 5 ) es la suma de un primo y el doble de un primo". ^[31] Esta conjetura se conoce como conjetura de Lemoine y también se llama conjetura de Levy .
• La conjetura de Goldbach para números prácticos , una secuencia de números enteros de tipo primo, fue enunciada por Margenstern en 1984, ^[32] y demostrada por Melfi en 1996: ^[33] todo número par es una suma de dos números prácticos.
• Harvey Dubner propuso un fortalecimiento de la conjetura de Goldbach que establece que todo entero par mayor que 4208 es la suma de dos primos gemelos (no necesariamente pertenecientes al mismo par). ^{[34] [ mejor fuente necesaria ]} Solo 34 enteros pares menores que 4208 no son la suma de dos primos gemelos; Dubner ha verificado computacionalmente que esta lista está completa hasta ^{[35] [ verificación necesaria ]} Una prueba de esta conjetura más fuerte no solo implicaría la conjetura de Goldbach, sino también la conjetura de los primos gemelos . ${\displaystyle 2\cdot 10^{10}.}$
• Según el postulado de Bertrand , para cada número entero , siempre hay al menos un primo tal que Si el postulado fuera falso, existiría algún número entero para el cual no hay números primos entre y , lo que haría imposible expresarlo como una suma de dos primos. ${\displaystyle n>1}$ ${\displaystyle p}$ ${\displaystyle n<p<2n.}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle 2n}$ ${\displaystyle 2n}$

La conjetura de Goldbach se utiliza al estudiar la complejidad computacional. ^[36] La conexión se realiza a través de la función Busy Beaver , donde BB( n ) es el número máximo de pasos dados por cualquier máquina de Turing de n estados que se detiene. Hay una máquina de Turing de 27 estados que se detiene si y solo si la conjetura de Goldbach es falsa. Por lo tanto, si se conociera BB(27), y la máquina de Goldbach no se detuviera en ese número de pasos, se sabría que funciona para siempre y, por lo tanto, no existen contraejemplos (lo que prueba que la conjetura es verdadera). Esta es una forma completamente impráctica de resolver la conjetura; en cambio, se utiliza para sugerir que BB(27) será muy difícil de calcular, al menos tan difícil como resolver la conjetura de Goldbach.

Referencias

1. Correspondance mathématique et physique de quelques célèbres géomètres du XVIIIème siècle (Banda 1), San Petersburgo 1843, págs.
2. http://www.math.dartmouth.edu/~euler/correspondence/letters/OO0765.pdf ^{[ URL básica PDF ]}
3. Weisstein, Eric W. "Conjetura de Goldbach". MathWorld .
4. En la versión impresa publicada por P. H. Fuss [1] 2 está mal impreso como 1 en la conjetura marginal.
5. http://eulerarchive.maa.org//correspondence/letters/OO0766.pdf ^{[ URL básica PDF ]}
6. Ingham, AE "Conferencias populares" (PDF) . Archivado desde el original (PDF) el 16 de junio de 2003. Consultado el 23 de septiembre de 2009 .
7. Caldwell, Chris (2008). «La conjetura de Goldbach» . Consultado el 13 de agosto de 2008 .
8. Chudakov, Nikolai G. (1937). " О проблеме Гольдбаха " [Sobre el problema de Goldbach]. Doklady Akademii Nauk SSSR . 17 : 335–338.
9. Van der Corput, JG (1938). "Sur l'hypothèse de Goldbach" (PDF) . Proc. Akád. Húmedo. Ámsterdam (en francés). 41 : 76–80.
10. Estermann, T. (1938). "Sobre el problema de Goldbach: prueba de que casi todos los números enteros positivos pares son sumas de dos primos". Proc. London Math. Soc . 2. 44 : 307–314. doi :10.1112/plms/s2-44.4.307.
11. Schnirelmann, L. G. (1930). "Sobre las propiedades aditivas de los números", publicado por primera vez en "Proceedings of the Don Polytechnic Institute in Novocherkassk" (en ruso), vol. 14 (1930), pp. 3-27, y reimpreso en "Uspekhi Matematicheskikh Nauk" (en ruso), 1939, núm. 6, 9-25.
12. Schnirelmann, LG (1933). Publicado por primera vez como "Über aditivo Eigenschaften von Zahlen" en " Mathematische Annalen " (en alemán), vol. 107 (1933), 649–690, y reimpreso como "Sobre las propiedades aditivas de los números" en "Uspekhi Matematicheskikh Nauk" (en ruso), 1940, núm. 7, 7–46.
13. Helfgott, HA (2013). "La conjetura ternaria de Goldbach es verdadera". arXiv : 1312.7748 [math.NT].
14. Sinisalo, Matti K. (octubre de 1993). "Comprobación de la conjetura de Goldbach hasta 4 ⋅ 1011" (PDF) . Matemáticas de la computación . 61 (204). Sociedad matemática estadounidense: 931–934. CiteSeerX 10.1.1.364.3111 . doi :10.2307/2153264. JSTOR  2153264. 
15. Rassias, M. Th. (2017). Problema de Goldbach: temas seleccionados . Springer.
16. Véase, por ejemplo, Una nueva fórmula explícita en la teoría aditiva de primos con aplicaciones I. La fórmula explícita para los problemas de Goldbach y de primos gemelos generalizados de Janos Pintz.
17. Rényi, AA (1948). "Sobre la representación de un número par como suma de un primo y un casi primo". Izvestiya Akademii Nauk SSSR Seriya Matematicheskaya (en ruso). 12 : 57–78.
18. Chen, JR (1973). "Sobre la representación de un entero par mayor como la suma de un primo y el producto de, como máximo, dos primos". Sci. Sinica . 16 : 157–176.
19. Pintz, J .; Ruzsa, IZ (01 de agosto de 2020). "Sobre la aproximación de Linnik al problema de Goldbach. II". Acta Mathematica Hungarica . 161 (2): 569–582. doi :10.1007/s10474-020-01077-8. ISSN  1588-2632. S2CID  54613256.
20. Heath-Brown, DR; Puchta, JC (2002). "Números enteros representados como suma de primos y potencias de dos". Revista asiática de matemáticas . 6 (3): 535–565. arXiv : math.NT/0201299 . Código Bibliográfico :2002math......1299H. doi :10.4310/AJM.2002.v6.n3.a7. S2CID  2843509.
21. Helfgott, HA (2013). "Arcos mayores para el teorema de Goldbach". arXiv : 1305.2897 [math.NT].
22. Helfgott, HA (2012). "Arcos menores para el problema de Goldbach". arXiv : 1205.5252 [math.NT].
23. "Harald Andrés Helfgott". Instituto de Matemáticas de Jussieu-Paris Rive Gauche . Consultado el 6 de abril de 2021 .
24. Pipping, Nils (1890-1982), "Die Goldbachsche Vermutung und der Goldbach-Vinogradowsche Satz". Acta Acad. Aboensis, Matemáticas. Física. 11, 4-25, 1938.
25. Tomás Oliveira e Silva, verificación de la conjetura de Goldbach. Consultado el 20 de abril de 2024.
26. Michaela Cully-Hugill y Adrian W. Dudek, Una estimación explícita del valor medio para el PNT en intervalos
27. "Matemáticas Ficción: Nadie que conozcas (Michelle Richmond)". kasmana.people.cofc.edu .
28. Odile Morain Le Théorème de Marguerite, en franciainfo:cultura
29. Fliegel, Henry F.; Robertson, Douglas S. (1989). "El cometa de Goldbach: los números relacionados con la conjetura de Goldbach". Revista de matemáticas recreativas . 21 (1): 1–7.
30. Sloane, N. J. A. (ed.). "Secuencia A066352 (secuencia de Pillai)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
31. Revista de Matemáticas , 66:1 (1993): 45–47.
32. Margenstern, M. (1984). "Resultados y conjeturas sobre números prácticos". Cuentas de resultados de la Academia de Ciencias . 299 : 895–898.
33. Melfi, G. (1996). "Sobre dos conjeturas acerca de números prácticos". Journal of Number Theory . 56 : 205–210. doi : 10.1006/jnth.1996.0012 .
34. "CONJETURAS DE LOS NUMEROS PRIMOS GEMELOS" (PDF) . oeis.org .
35. Sloane, N. J. A. (ed.). "Secuencia A007534 (Números pares que no son la suma de un par de primos gemelos)". La enciclopedia en línea de secuencias de números enteros . Fundación OEIS.
36. "Cómo los programas informáticos más lentos iluminan los límites fundamentales de las matemáticas".

Lectura adicional

• Deshouillers, J.-M.; Effinger, G.; te Riele, H.; Zinoviev, D. (1997). "Un teorema completo de Vinogradov de 3 primos bajo la hipótesis de Riemann" (PDF) . Anuncios electrónicos de investigación de la American Mathematical Society . 3 (15): 99–104. doi : 10.1090/S1079-6762-97-00031-0 .
• Montgomery, HL; Vaughan, RC (1975). "El conjunto excepcional en el problema de Goldbach" (PDF) . Acta Arithmetica . 27 : 353–370. doi : 10.4064/aa-27-1-353-370 .
• Terence Tao demostró que todos los números impares son como máximo la suma de cinco primos.
• Conjetura de Goldbach en MathWorld .

Enlaces externos

• Medios relacionados con la conjetura de Goldbach en Wikimedia Commons
• "Problema de Goldbach", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Carta original de Goldbach a Euler — formato PDF (en alemán y latín)
• Conjetura de Goldbach, parte de Prime Pages de Chris Caldwell .
• Verificación de la conjetura de Goldbach, búsqueda informática distribuida de Tomás Oliveira e Silva.