El flujo compresible (o dinámica de gases ) es la rama de la mecánica de fluidos que se ocupa de los flujos que tienen cambios significativos en la densidad del fluido . Si bien todos los flujos son compresibles , los flujos generalmente se tratan como incompresibles cuando el número de Mach (la relación entre la velocidad del flujo y la velocidad del sonido) es menor que 0,3 (ya que el cambio de densidad debido a la velocidad es de aproximadamente el 5 % en ese caso). [1] El estudio del flujo compresible es relevante para aeronaves de alta velocidad, motores a reacción, motores de cohetes, entrada a alta velocidad en una atmósfera planetaria, gasoductos, aplicaciones comerciales como el chorro abrasivo y muchos otros campos.
El estudio de la dinámica de los gases suele asociarse con el vuelo de aeronaves modernas de alta velocidad y la reentrada atmosférica de vehículos de exploración espacial; sin embargo, sus orígenes se encuentran en máquinas más simples. A principios del siglo XIX, la investigación sobre el comportamiento de las balas disparadas condujo a una mejora en la precisión y las capacidades de los cañones y la artillería. [2] A medida que avanzaba el siglo, inventores como Gustaf de Laval hicieron avanzar el campo, mientras que investigadores como Ernst Mach intentaron comprender los fenómenos físicos involucrados mediante la experimentación.
A principios del siglo XX, el foco de la investigación de la dinámica de los gases se desplazó a lo que eventualmente se convertiría en la industria aeroespacial. Ludwig Prandtl y sus estudiantes propusieron conceptos importantes que abarcaban desde la capa límite hasta las ondas de choque supersónicas , los túneles de viento supersónicos y el diseño de toberas supersónicas. [2] Theodore von Kármán , un estudiante de Prandtl, continuó mejorando la comprensión del flujo supersónico. Otras figuras notables ( Meyer , Luigi Crocco y Ascher Shapiro ) también contribuyeron significativamente a los principios considerados fundamentales para el estudio de la dinámica de los gases moderna. Muchos otros también contribuyeron a este campo.
A principios del siglo XX, junto con la mejora de la comprensión conceptual de la dinámica de los gases, se creó una idea errónea de que existía una barrera para la velocidad alcanzable de los aviones, comúnmente conocida como la " barrera del sonido ". En realidad, la barrera para el vuelo supersónico era meramente tecnológica, aunque era una barrera difícil de superar. Entre otros factores, los perfiles aerodinámicos convencionales experimentaron un aumento dramático en el coeficiente de resistencia cuando el flujo se acercaba a la velocidad del sonido. Superar la mayor resistencia resultó difícil con los diseños contemporáneos, de ahí la percepción de una barrera del sonido. Sin embargo, el diseño de aeronaves progresó lo suficiente como para producir el Bell X-1 . Pilotado por Chuck Yeager , el X-1 alcanzó oficialmente la velocidad supersónica en octubre de 1947. [3]
Históricamente, se han seguido dos caminos paralelos de investigación para profundizar en el conocimiento de la dinámica de los gases. La dinámica de los gases experimental lleva a cabo experimentos con modelos de túneles de viento y experimentos en tubos de choque y campos balísticos con el uso de técnicas ópticas para documentar los hallazgos. La dinámica de los gases teórica considera las ecuaciones de movimiento aplicadas a un gas de densidad variable y sus soluciones. Gran parte de la dinámica de los gases básica es analítica, pero en la era moderna la dinámica de fluidos computacional aplica la potencia de computación para resolver las ecuaciones diferenciales parciales no lineales de flujo compresible, que de otro modo serían intratables, para geometrías y características de flujo específicas.

La teoría subyacente del flujo compresible se basa en varios supuestos importantes. Todos los fluidos están compuestos de moléculas, pero no es necesario rastrear una gran cantidad de moléculas individuales en un flujo (por ejemplo, a presión atmosférica). En cambio, el supuesto del continuo nos permite considerar un gas que fluye como una sustancia continua, excepto a bajas densidades. Este supuesto proporciona una enorme simplificación que es precisa para la mayoría de los problemas de dinámica de gases. Solo en el ámbito de baja densidad de la dinámica de gases enrarecidos el movimiento de moléculas individuales se vuelve importante.
Un supuesto relacionado es la condición de no deslizamiento, en la que se supone que la velocidad del flujo en una superficie sólida es igual a la velocidad de la superficie misma, lo que es una consecuencia directa de suponer un flujo continuo. La condición de no deslizamiento implica que el flujo es viscoso y, como resultado, se forma una capa límite en los cuerpos que viajan por el aire a altas velocidades, de forma muy similar a como ocurre en el flujo a baja velocidad.
La mayoría de los problemas de flujo incompresible involucran sólo dos incógnitas: presión y velocidad, que se encuentran típicamente resolviendo las dos ecuaciones que describen la conservación de la masa y del momento lineal, con la densidad del fluido supuesta constante. En el flujo compresible, sin embargo, la densidad del gas y la temperatura también se vuelven variables. Esto requiere dos ecuaciones más para resolver problemas de flujo compresible: una ecuación de estado para el gas y una ecuación de conservación de la energía . Para la mayoría de los problemas de dinámica de gases, la ley de los gases ideales es la ecuación de estado apropiada. De lo contrario, se deben considerar ecuaciones de estado más complejas y se establece la llamada dinámica de fluidos compresibles no ideales (NICFD).
Los problemas de dinámica de fluidos tienen dos tipos generales de marcos de referencia, llamados lagrangiano y euleriano (ver Joseph-Louis Lagrange y Leonhard Euler ). El enfoque lagrangiano sigue una masa fluida de identidad fija a medida que se mueve a través de un campo de flujo. El marco de referencia euleriano, por el contrario, no se mueve con el fluido. Más bien es un marco fijo o volumen de control a través del cual fluye el fluido. El marco euleriano es más útil en la mayoría de los problemas de flujo compresible, pero requiere que las ecuaciones de movimiento se escriban en un formato compatible.
Por último, aunque se sabe que el espacio tiene tres dimensiones, se puede lograr una simplificación importante al describir matemáticamente la dinámica de los gases si solo una dimensión espacial es de importancia primaria, por lo que se supone que el flujo es unidimensional. Esto funciona bien en flujos en conductos, toberas y difusores, donde las propiedades del flujo cambian principalmente en la dirección del flujo en lugar de perpendicularmente al flujo. Sin embargo, una clase importante de flujos compresibles, incluido el flujo externo sobre cuerpos que viajan a alta velocidad, requiere al menos un tratamiento bidimensional. Cuando las tres dimensiones espaciales y quizás también la dimensión temporal son importantes, a menudo recurrimos a soluciones computarizadas de las ecuaciones que gobiernan.
El número de Mach (M) se define como la relación entre la velocidad de un objeto (o de un flujo) y la velocidad del sonido. Por ejemplo, en el aire a temperatura ambiente, la velocidad del sonido es de unos 340 m/s (1100 pies/s). M puede variar de 0 a ∞, pero este amplio rango se divide naturalmente en varios regímenes de flujo. Estos regímenes son el subsónico, el transónico , el supersónico , el hipersónico y el de hipervelocidad . La siguiente figura ilustra el "espectro" del número de Mach de estos regímenes de flujo.
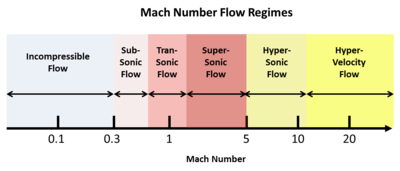
Estos regímenes de flujo no se eligen de manera arbitraria, sino que surgen de manera natural de la sólida base matemática que subyace al flujo compresible (véanse los libros de referencia citados). A velocidades de flujo muy lentas, la velocidad del sonido es tan rápida que se ignora matemáticamente y el número de Mach es irrelevante. Sin embargo, una vez que la velocidad del flujo se acerca a la velocidad del sonido, el número de Mach se vuelve sumamente importante y comienzan a aparecer ondas de choque. Por lo tanto, el régimen transónico se describe mediante un tratamiento matemático diferente (y mucho más complejo). En el régimen supersónico, el flujo está dominado por el movimiento de las ondas en ángulos oblicuos similares al ángulo de Mach. Por encima de aproximadamente Mach 5, estos ángulos de onda se vuelven tan pequeños que se requiere un enfoque matemático diferente, que define el régimen de velocidad hipersónica . Finalmente, a velocidades comparables a la de la entrada atmosférica planetaria desde la órbita, en el rango de varios km/s, la velocidad del sonido ahora es comparativamente tan lenta que una vez más se ignora matemáticamente en el régimen de hipervelocidad .
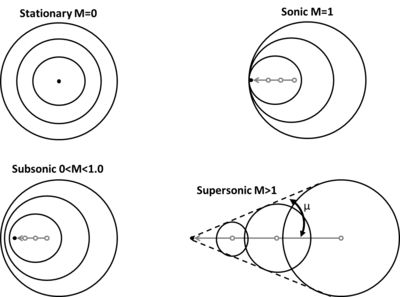
A medida que un objeto acelera desde una velocidad subsónica a una supersónica en un gas, se producen diferentes tipos de fenómenos ondulatorios. Para ilustrar estos cambios, la siguiente figura muestra un punto estacionario (M = 0) que emite ondas sonoras simétricas. La velocidad del sonido es la misma en todas las direcciones en un fluido uniforme, por lo que estas ondas son simplemente esferas concéntricas. A medida que el punto generador del sonido comienza a acelerar, las ondas sonoras se "amontonan" en la dirección del movimiento y se "estiran" en la dirección opuesta. Cuando el punto alcanza la velocidad del sonido (M = 1), viaja a la misma velocidad que las ondas sonoras que crea. Por lo tanto, un número infinito de estas ondas sonoras se "apilan" delante del punto, formando una onda de choque . Al alcanzar el flujo supersónico, la partícula se mueve tan rápido que deja continuamente sus ondas sonoras atrás. Cuando esto ocurre, el lugar geométrico de estas ondas que se arrastran detrás del punto crea un ángulo conocido como ángulo de onda de Mach o ángulo de Mach, μ:
donde representa la velocidad del sonido en el gas y representa la velocidad del objeto. Aunque se denominan así por el físico austríaco Ernst Mach , estas ondas oblicuas fueron descubiertas por primera vez por Christian Doppler . [4]
El flujo unidimensional (1-D) se refiere al flujo de gas a través de un conducto o canal en el que se supone que los parámetros de flujo cambian significativamente a lo largo de una sola dimensión espacial, es decir, la longitud del conducto. Al analizar el flujo de canal unidimensional, se realizan una serie de suposiciones:
A medida que la velocidad de un flujo se acelera desde el régimen subsónico al supersónico, se altera la física de los flujos en las toberas y difusores. Utilizando las leyes de conservación de la dinámica de fluidos y la termodinámica, se desarrolla la siguiente relación para el flujo en canal (conservación combinada de masa y momento):
donde dP es el cambio diferencial de presión, M es el número de Mach, ρ es la densidad del gas, V es la velocidad del flujo, A es el área del conducto y dA es el cambio en el área del conducto. Esta ecuación establece que, para el flujo subsónico, un conducto convergente (dA < 0) aumenta la velocidad del flujo y un conducto divergente (dA > 0) disminuye la velocidad del flujo. Para el flujo supersónico, ocurre lo opuesto debido al cambio de signo de (1 − M 2 ). Un conducto convergente (dA < 0) ahora disminuye la velocidad del flujo y un conducto divergente (dA > 0) aumenta la velocidad del flujo. En Mach = 1, ocurre un caso especial en el que el área del conducto debe ser máxima o mínima. Para fines prácticos, solo un área mínima puede acelerar los flujos a Mach 1 y más. Consulte la tabla de difusores y toberas subsupersónicos.
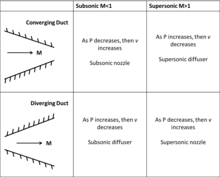
Por lo tanto, para acelerar un flujo a Mach 1, se debe diseñar una tobera para que converja hasta un área de sección transversal mínima y luego se expanda. Este tipo de tobera, la tobera convergente-divergente, se llama tobera de Laval en honor a Gustaf de Laval , quien la inventó. A medida que el flujo subsónico ingresa al conducto convergente y el área disminuye, el flujo se acelera. Al alcanzar el área mínima del conducto, también conocida como la garganta de la tobera, el flujo puede alcanzar Mach 1. Si la velocidad del flujo continúa aumentando, su densidad debe disminuir para obedecer la conservación de la masa. Para lograr esta disminución de la densidad, el flujo debe expandirse y, para ello, el flujo debe pasar a través de un conducto divergente. Ver imagen de la tobera de Laval.

En última instancia, debido a la ley de conservación de la energía, un gas está limitado a una determinada velocidad máxima en función de su contenido energético. La velocidad máxima, Vmax , que puede alcanzar un gas es:
donde c p es el calor específico del gas y T t es la temperatura de estancamiento del flujo.
Utilizando las leyes de conservación y la termodinámica, se obtienen varias relaciones de la forma
se puede obtener, donde M es el número de Mach y γ es la relación de calores específicos (1,4 para el aire). Véase la tabla de relaciones de números de Mach de flujo isentrópico.
Como se mencionó anteriormente, para que un flujo se vuelva supersónico, debe pasar a través de un conducto con un área mínima, o garganta sónica. Además, se necesita una relación de presión general, P b /P t , de aproximadamente 2 para alcanzar Mach 1. Una vez que ha alcanzado Mach 1, se dice que el flujo en la garganta está estrangulado . Debido a que los cambios aguas abajo solo pueden moverse aguas arriba a velocidad sónica, el flujo másico a través de la boquilla no puede verse afectado por los cambios en las condiciones aguas abajo después de que el flujo se estrangula.
Las ondas de choque normales son ondas de choque perpendiculares a la dirección del flujo local. Estas ondas de choque se producen cuando las ondas de presión se acumulan y se fusionan en una onda de choque extremadamente delgada que convierte la energía cinética en energía térmica . De este modo, las ondas se superan y se refuerzan entre sí, formando una onda de choque finita a partir de una serie infinita de ondas sonoras infinitesimales. Debido a que el cambio de estado a través del choque es altamente irreversible, la entropía aumenta a través del choque. Al analizar una onda de choque normal, se supone un flujo unidimensional, constante y adiabático de un gas perfecto. La temperatura y la entalpía de estancamiento son las mismas aguas arriba y aguas abajo del choque.
Las ondas de choque normales se pueden analizar fácilmente en cualquiera de dos marcos de referencia: el choque normal en reposo y el choque en movimiento. El flujo antes de una onda de choque normal debe ser supersónico, y el flujo después de un choque normal debe ser subsónico. Las ecuaciones de Rankine-Hugoniot se utilizan para calcular las condiciones de flujo.
Aunque el flujo unidimensional puede analizarse directamente, es simplemente un caso especializado de flujo bidimensional. De ello se deduce que uno de los fenómenos definitorios del flujo unidimensional, un choque normal, es también sólo un caso especial de una clase más amplia de choques oblicuos . Además, el nombre "normal" se refiere a la geometría en lugar de a la frecuencia de ocurrencia. Los choques oblicuos son mucho más comunes en aplicaciones tales como: diseño de entradas de aeronaves, objetos en vuelo supersónico y (a un nivel más fundamental) toberas y difusores supersónicos. Dependiendo de las condiciones del flujo, un choque oblicuo puede estar unido al flujo o separado del flujo en forma de un choque de arco .
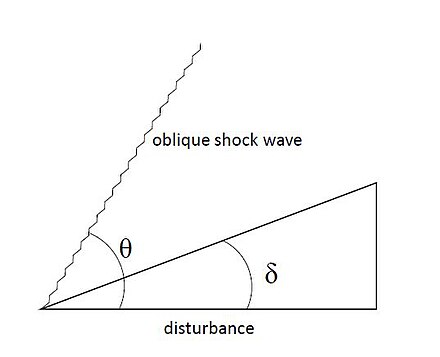
Las ondas de choque oblicuas son similares a las ondas de choque normales, pero se producen en ángulos menores a 90° con respecto a la dirección del flujo. Cuando se introduce una perturbación en el flujo en un ángulo distinto de cero (δ), el flujo debe responder a las condiciones de contorno cambiantes. Por lo tanto, se forma un choque oblicuo, lo que da como resultado un cambio en la dirección del flujo.

Según el nivel de desviación del flujo (δ), los choques oblicuos se caracterizan como fuertes o débiles. Los choques fuertes se caracterizan por una desviación mayor y una mayor pérdida de entropía a lo largo del choque, mientras que los choques débiles son lo opuesto. Para obtener una idea superficial de las diferencias entre estos choques, se puede utilizar un diagrama polar de choques. Conocida la temperatura estática después del choque, T*, la velocidad del sonido después del choque se define como,
con R como la constante de los gases y γ como la relación de calores específicos. El número de Mach se puede descomponer en coordenadas cartesianas.
con V x y V y como los componentes x e y de la velocidad del fluido V. Con el número de Mach antes del choque dado, se puede especificar un lugar geométrico de condiciones. En algún δ max , el flujo pasa de un choque oblicuo fuerte a uno débil. Con δ = 0°, se produce un choque normal en el límite del choque oblicuo fuerte y la onda de Mach se produce en el límite de la onda de choque débil.
Debido a la inclinación del choque, después de crearse un choque oblicuo, puede interactuar con un límite de tres maneras diferentes, dos de las cuales se explican a continuación.
El flujo entrante primero se desvía en un ángulo δ con respecto al flujo. Esta onda de choque se refleja en el límite sólido y el flujo se desvía en un ángulo – δ para volver a ser paralelo al límite. Cada onda de choque progresiva es más débil y el ángulo de onda aumenta.
Una reflexión irregular es muy similar al caso descrito anteriormente, con la salvedad de que δ es mayor que el ángulo de giro máximo permitido. Por lo tanto, se forma un choque desprendido y se produce una reflexión más complicada conocida como reflexión de Mach.
Los abanicos Prandtl-Meyer pueden expresarse como abanicos de compresión y de expansión. Los abanicos Prandtl-Meyer también cruzan una capa límite (es decir, fluida y sólida) que reacciona con diferentes cambios también. Cuando una onda de choque golpea una superficie sólida, el abanico resultante regresa como uno de la familia opuesta, mientras que cuando uno golpea un límite libre, el abanico regresa como un abanico de tipo opuesto.

Hasta el momento, los únicos fenómenos de flujo que se han analizado son las ondas de choque, que ralentizan el flujo y aumentan su entropía. Es posible acelerar el flujo supersónico en lo que se ha denominado abanico de expansión Prandtl-Meyer , en honor a Ludwig Prandtl y Theodore Meyer. El mecanismo de expansión se muestra en la siguiente figura.
A diferencia del flujo que encuentra una obstrucción inclinada y forma un choque oblicuo, el flujo se expande alrededor de una esquina convexa y forma un abanico de expansión a través de una serie de ondas de Mach isentrópicas. El "abanico" de expansión está compuesto de ondas de Mach que abarcan desde el ángulo de Mach inicial hasta el ángulo de Mach final. El flujo puede expandirse tanto alrededor de una esquina aguda como de una redondeada por igual, ya que el aumento del número de Mach es proporcional solo al ángulo convexo del paso (δ). La esquina de expansión que produce el abanico de Prandtl-Meyer puede ser aguda (como se ilustra en la figura) o redondeada. Si el ángulo de giro total es el mismo, entonces la solución de flujo de PM también es la misma.
La expansión de Prandtl-Meyer puede considerarse como la explicación física del funcionamiento de la tobera de Laval. El contorno de la tobera crea una serie suave y continua de ondas de expansión de Prandtl-Meyer.

Una compresión de Prandtl-Meyer es el fenómeno opuesto a una expansión de Prandtl-Meyer. Si el flujo se gira gradualmente en un ángulo de δ, se puede formar un abanico de compresión. Este abanico es una serie de ondas de Mach que finalmente se fusionan en un choque oblicuo. Debido a que el flujo está definido por una región isentrópica (flujo que viaja a través del abanico) y una región anisentrópica (flujo que viaja a través del choque oblicuo), se produce una línea de deslizamiento entre las dos regiones de flujo.
Los túneles de viento supersónicos se utilizan para realizar pruebas e investigaciones en flujos supersónicos, aproximadamente en el rango de números de Mach de 1,2 a 5. El principio de funcionamiento del túnel de viento es que se mantiene una gran diferencia de presión entre aguas arriba y aguas abajo, lo que impulsa el flujo.

Los túneles de viento se pueden dividir en dos categorías: túneles de viento de funcionamiento continuo y túneles de viento de funcionamiento intermitente. Los túneles de viento supersónicos de funcionamiento continuo requieren una fuente de energía eléctrica independiente que aumenta drásticamente con el tamaño de la sección de prueba. Los túneles de viento supersónicos intermitentes son menos costosos porque almacenan energía eléctrica durante un período prolongado de tiempo y luego la descargan durante una serie de pruebas breves. La diferencia entre estos dos es análoga a la comparación entre una batería y un condensador.
Los túneles de viento supersónicos de tipo purga ofrecen un alto número de Reynolds, un pequeño tanque de almacenamiento y aire seco fácilmente disponible. Sin embargo, generan un riesgo de alta presión, dificultan el mantenimiento de una presión de estancamiento constante y son ruidosos durante su funcionamiento.
Los túneles de viento supersónicos de tiro interno no están asociados a riesgos de presión, permiten una presión de estancamiento constante y son relativamente silenciosos. Desafortunadamente, tienen un rango limitado para el número de Reynolds del flujo y requieren un tanque de vacío grande.
No hay duda de que el conocimiento se obtiene mediante la investigación y las pruebas en túneles de viento supersónicos; sin embargo, las instalaciones a menudo requieren grandes cantidades de energía para mantener las grandes relaciones de presión necesarias para las condiciones de prueba. Por ejemplo, Arnold Engineering Development Complex tiene el túnel de viento supersónico más grande del mundo y requiere la energía necesaria para iluminar una ciudad pequeña para su funcionamiento. Por esta razón, los grandes túneles de viento son cada vez menos comunes en las universidades.
Tal vez el requisito más común para los amortiguadores oblicuos se encuentra en las entradas de los aviones supersónicos para velocidades superiores a Mach 2 (el F-16 tiene una velocidad máxima de Mach 2, pero no necesita una entrada de amortiguadores oblicuos). Uno de los propósitos de la entrada es minimizar las pérdidas a través de los amortiguadores a medida que el aire supersónico entrante se desacelera a subsónico antes de ingresar al motor turborreactor. Esto se logra con uno o más amortiguadores oblicuos seguidos de un amortiguador normal muy débil, con un número de Mach ascendente generalmente menor a 1,4. El flujo de aire a través de la entrada debe gestionarse correctamente en un amplio rango de velocidades desde cero hasta su velocidad supersónica máxima. Esto se hace variando la posición de las superficies de entrada.
Aunque se requiere una geometría variable para lograr un rendimiento aceptable desde el despegue hasta velocidades superiores a Mach 2, no existe un único método para lograrlo. Por ejemplo, para una velocidad máxima de aproximadamente Mach 3, el XB-70 utilizó entradas rectangulares con rampas ajustables y el SR-71 utilizó entradas circulares con cono de entrada ajustable .