Capacidad calorífica específica

Calor necesario para aumentar la temperatura de una unidad dada de masa de una sustancia

En termodinámica , la capacidad calorífica específica (símbolo c ) de una sustancia es la cantidad de calor que debe añadirse a una unidad de masa de la sustancia para provocar un aumento de una unidad en la temperatura . También se conoce como capacidad calorífica másica o como calor específico. Más formalmente, es la capacidad calorífica de una muestra de la sustancia dividida por la masa de la muestra. ^[1] La unidad SI de capacidad calorífica específica es julio por kelvin por kilogramo , J⋅kg ⁻¹ ⋅K ⁻¹ . ^[2] Por ejemplo, el calor necesario para elevar la temperatura de1 kg de agua por1 K es4184 julios , por lo que la capacidad calorífica específica del agua es4184 J⋅kg ⁻¹ ⋅K ⁻¹ . ^[3]

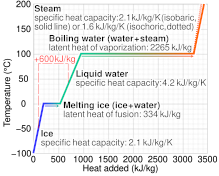
La capacidad calorífica específica a menudo varía con la temperatura y es diferente para cada estado de la materia . El agua líquida tiene una de las capacidades caloríficas específicas más altas entre las sustancias comunes, aproximadamente4184 J⋅kg ⁻¹ ⋅K ⁻¹ a 20 °C; pero la del hielo, justo por debajo de 0 °C, es sólo2093 J⋅kg ⁻¹ ⋅K ⁻¹ . Las capacidades caloríficas específicas del hierro , el granito y el gas hidrógeno son aproximadamente 449 J⋅kg ⁻¹ ⋅K ⁻¹ , 790 J⋅kg ⁻¹ ⋅K ⁻¹ y 14300 J⋅kg ⁻¹ ⋅K ⁻¹ , respectivamente. ^[4] Mientras la sustancia está experimentando una transición de fase , como la fusión o la ebullición, su capacidad calorífica específica no está definida técnicamente, porque el calor se destina a cambiar su estado en lugar de aumentar su temperatura.

La capacidad calorífica específica de una sustancia, especialmente de un gas, puede ser significativamente mayor cuando se le permite expandirse mientras se calienta (capacidad calorífica específica a presión constante ) que cuando se calienta en un recipiente cerrado que evita la expansión (capacidad calorífica específica a volumen constante ). Estos dos valores se denotan generalmente por y , respectivamente; su cociente es el cociente de capacidades caloríficas . ${\displaystyle c_{p}}$ ${\displaystyle c_{V}}$ ${\displaystyle \gamma =c_{p}/c_{V}}$

El término calor específico también puede referirse a la relación entre las capacidades caloríficas específicas de una sustancia a una temperatura dada y de una sustancia de referencia a una temperatura de referencia, como el agua a 15 °C; ^[5] muy a la manera de la gravedad específica . La capacidad calorífica específica también está relacionada con otras medidas intensivas de capacidad calorífica con otros denominadores. Si la cantidad de sustancia se mide como un número de moles , se obtiene la capacidad calorífica molar , cuya unidad SI es julio por kelvin por mol, J⋅mol ⁻¹ ⋅K ⁻¹ . Si la cantidad se toma como el volumen de la muestra (como a veces se hace en ingeniería), se obtiene la capacidad calorífica volumétrica , cuya unidad SI es julio por kelvin por metro cúbico , J⋅m ⁻³ ⋅K ⁻¹ .

Historia

Descubrimiento del calor específico

José negro

Uno de los primeros científicos en utilizar el concepto fue Joseph Black , un médico del siglo XVIII y profesor de medicina en la Universidad de Glasgow . Midió las capacidades caloríficas específicas de muchas sustancias, utilizando el término capacidad de calor . ^[6] En 1756 o poco después, Black comenzó un estudio extenso del calor. ^[7] En 1760 se dio cuenta de que cuando se mezclan dos sustancias diferentes de igual masa pero diferentes temperaturas, los cambios en el número de grados en las dos sustancias difieren, aunque el calor ganado por la sustancia más fría y perdido por la más caliente es el mismo. Black relató un experimento realizado por Daniel Gabriel Fahrenheit en nombre del médico holandés Herman Boerhaave . Para mayor claridad, luego describió una variante hipotética, pero realista del experimento: si se mezclan masas iguales de agua a 100 °F y mercurio a 150 °F, la temperatura del agua aumenta en 20 ° y la temperatura del mercurio disminuye en 30 ° (ambas llegan a 120 °F), aunque el calor ganado por el agua y perdido por el mercurio es el mismo. Esto aclaró la distinción entre calor y temperatura. También introdujo el concepto de capacidad calorífica específica, que es diferente para distintas sustancias. Black escribió: “El mercurio... tiene menos capacidad para la materia de calor que el agua”. ^{[8] [9]}

Definición

La capacidad calorífica específica de una sustancia, usualmente denotada por o , es la capacidad calorífica de una muestra de la sustancia, dividida por la masa de la muestra: ^[10] donde representa la cantidad de calor necesaria para elevar uniformemente la temperatura de la muestra en un pequeño incremento . ${\displaystyle c}$ ${\displaystyle s}$ ${\displaystyle C}$ ${\displaystyle M}$ $${\displaystyle c={\frac {C}{M}}={\frac {1}{M}}\cdot {\frac {\mathrm {d} Q}{\mathrm {d} T}},}$$ ${\displaystyle \mathrm {d} Q}$ ${\displaystyle \mathrm {d} T}$

Al igual que la capacidad calorífica de un objeto, la capacidad calorífica específica de una sustancia puede variar, a veces de forma sustancial, en función de la temperatura inicial de la muestra y de la presión que se le aplica. Por lo tanto, debe considerarse una función de esas dos variables. ${\displaystyle T}$ ${\displaystyle p}$ ${\displaystyle c(p,T)}$

Estos parámetros se suelen especificar al indicar la capacidad calorífica específica de una sustancia. Por ejemplo, "Agua (líquida): = 4187 J⋅kg ⁻¹ ⋅K ⁻¹ (15 °C)". ^[11] Cuando no se especifican, los valores publicados de la capacidad calorífica específica generalmente son válidos para algunas condiciones estándar de temperatura y presión . ${\displaystyle c_{p}}$ ${\displaystyle c}$

Sin embargo, la dependencia de la temperatura y la presión iniciales a menudo se puede ignorar en contextos prácticos, por ejemplo, cuando se trabaja en rangos estrechos de esas variables. En esos contextos, se suele omitir el calificador y aproximar la capacidad calorífica específica mediante una constante adecuada para esos rangos. ${\displaystyle c}$ ${\displaystyle (p,T)}$ ${\displaystyle c}$

El calor específico es una propiedad intensiva de una sustancia, una característica intrínseca que no depende del tamaño o la forma de la cantidad considerada. (El calificativo "específico" antes de una propiedad extensiva a menudo indica una propiedad intensiva derivada de ella. ^[12] )

Variaciones

La inyección de energía térmica en una sustancia, además de aumentar su temperatura, suele provocar un aumento de su volumen y/o de su presión, dependiendo de cómo esté confinada la muestra. La elección que se haga de esta última afecta al calor específico medido, incluso para la misma presión y temperatura de partida . Se utilizan dos opciones en particular: ${\displaystyle p}$ ${\displaystyle T}$

• Si la presión se mantiene constante (por ejemplo, a la presión atmosférica ambiental) y se permite que la muestra se expanda, la expansión genera trabajo , ya que la fuerza de la presión desplaza el recinto o el fluido circundante. Ese trabajo debe provenir de la energía térmica proporcionada. Se dice que la capacidad calorífica específica así obtenida se mide a presión constante (o isobárica ) y a menudo se denota . ${\displaystyle c_{p}}$
• Por otra parte, si se evita la expansión (por ejemplo, mediante un recinto suficientemente rígido o aumentando la presión externa para contrarrestar la interna), no se genera trabajo y la energía térmica que habría entrado en ella debe contribuir en cambio a la energía interna de la muestra, incluido el aumento de su temperatura en una cantidad adicional. Se dice que la capacidad calorífica específica obtenida de esta manera se mide a volumen constante (o isocórica ) y se denota como . ${\displaystyle c_{V}}$

El valor de es siempre menor que el valor de para todos los fluidos. ^{[13] [14]} Esta diferencia es particularmente notable en los gases, donde los valores a presión constante son típicamente entre un 30% y un 66,7% mayores que los de volumen constante. Por lo tanto, la relación de capacidad térmica de los gases suele estar entre 1,3 y 1,67. ^[15] ${\displaystyle c_{V}}$ ${\displaystyle c_{p}}$

Aplicabilidad

La capacidad calorífica específica se puede definir y medir para gases, líquidos y sólidos de composición y estructura molecular bastante generales. Entre ellos se incluyen mezclas de gases, soluciones y aleaciones, o materiales heterogéneos como leche, arena, granito y hormigón, si se consideran a una escala suficientemente grande.

El calor específico puede definirse también para materiales que cambian de estado o composición al variar la temperatura y la presión, siempre que los cambios sean reversibles y graduales. Así, por ejemplo, los conceptos son definibles para un gas o líquido que se disocia al aumentar la temperatura, siempre que los productos de la disociación se recombinen rápida y completamente cuando se descompone.

La capacidad calorífica específica no es significativa si la sustancia sufre cambios químicos irreversibles o si hay un cambio de fase , como fusión o ebullición, a una temperatura brusca dentro del rango de temperaturas abarcado por la medición.

Medición

La capacidad calorífica específica de una sustancia se determina normalmente según la definición, es decir, midiendo la capacidad calorífica de una muestra de la sustancia, normalmente con un calorímetro , y dividiéndola por la masa de la muestra. Se pueden aplicar varias técnicas para estimar la capacidad calorífica de una sustancia, como la calorimetría diferencial de barrido . ^{[16] [17]}

Gráfico de temperatura de las fases del agua calentada de -100 °C a 200 °C : el ejemplo de la línea discontinua muestra que para derretir y calentar 1 kg de hielo a -50 °C hasta agua a 40 °C se necesitan 600 kJ.

Las capacidades caloríficas específicas de los gases se pueden medir a volumen constante, encerrando la muestra en un recipiente rígido. Por otra parte, medir la capacidad calorífica específica a volumen constante puede ser prohibitivamente difícil para líquidos y sólidos, ya que a menudo se necesitarían presiones poco prácticas para evitar la expansión que se produciría incluso con pequeños aumentos de temperatura. En cambio, la práctica habitual es medir la capacidad calorífica específica a presión constante (permitiendo que el material se expanda o contraiga como desee), determinar por separado el coeficiente de expansión térmica y la compresibilidad del material, y calcular la capacidad calorífica específica a volumen constante a partir de estos datos de acuerdo con las leyes de la termodinámica. ^{[ cita requerida ]}

Unidades

Sistema internacional

La unidad del SI para la capacidad calorífica específica es julio por kelvin por kilogramo .Yo/kg⋅K⁠ , J⋅K ⁻¹ ⋅kg ⁻¹ . Como un incremento de temperatura de un grado Celsius es lo mismo que un incremento de un kelvin, es decir, lo mismo que julio por grado Celsius por kilogramo: J/(kg⋅°C). A veces se utiliza el gramo en lugar del kilogramo como unidad de masa: 1 J⋅g ⁻¹ ⋅K ⁻¹ = 1000 J⋅kg ⁻¹ ⋅K ⁻¹ .

La capacidad calorífica específica de una sustancia (por unidad de masa) tiene dimensión L ² ⋅Θ ⁻¹ ⋅T ⁻² , o (L/T) ² /Θ. Por lo tanto, la unidad del SI J⋅kg ⁻¹ ⋅K ⁻¹ es equivalente a metro cuadrado por segundo al cuadrado por kelvin (m ² ⋅K ⁻¹ ⋅s ⁻² ).

Unidades de ingeniería imperial

Los profesionales de la construcción , la ingeniería civil , la ingeniería química y otras disciplinas técnicas, especialmente en los Estados Unidos , pueden utilizar unidades de ingeniería inglesas, incluida la libra (lb = 0,45359237 kg) como unidad de masa, el grado Fahrenheit o Rankine (°R = ⁠5/9⁠ K, aproximadamente 0,555556 K) como unidad de incremento de temperatura, y la unidad térmica británica (BTU ≈ 1055,056 J), ^{[18] [19]} como unidad de calor.

En esos contextos, la unidad de capacidad calorífica específica es BTU/lb⋅°R, o 1 ⁠BTU/lb⋅°R⁠ = 4186,68 ⁠Yo/kg⋅K⁠ . ^[20] La BTU se definió originalmente de modo que la capacidad calorífica específica promedio del agua fuera 1 BTU/lb⋅°F. ^[21] Nótese la similitud del valor con el de la caloría - 4187 J/kg⋅°C ≈ 4184 J/kg⋅°C (~.07%) - ya que esencialmente miden la misma energía, usando el agua como referencia base, escalada a las respectivas lbs y °F o kg y °C de sus sistemas.

Calorias

En química, las cantidades de calor se medían a menudo en calorías . Aunque puede resultar confuso, existen dos unidades comunes con ese nombre, denominadas cal y cal respectivamente :

• La caloría pequeña ( caloría-gramo, cal ) es exactamente 4,184 J. Originalmente se definió de modo que el calor específico del agua líquida fuera 1 cal/(°C⋅g).
• La caloría máxima ( kilocaloría, kilogramo-caloría, caloría alimentaria, kcal, Cal ) son 1000 calorías pequeñas, exactamente 4184 J. Se definió de modo que el calor específico del agua fuera 1 Cal/(°C⋅kg).

Si bien estas unidades aún se utilizan en algunos contextos (como el kilogramo de caloría en nutrición ), su uso está ahora en desuso en los campos técnicos y científicos. Cuando el calor se mide en estas unidades, la unidad de capacidad calorífica específica suele ser:

1  ⁠California/°C⋅g⁠ = 1  ⁠California/°C⋅kg⁠ = 1  ⁠kcal/°C⋅kg⁠ = 4184  ⁠Yo/kg⋅K⁠ ^[22] = 4,184  ⁠kJ/kg⋅K⁠ .

Tenga en cuenta que si bien cal es 1 ⁄ 1000 de una cal o kcal, también es por gramo en lugar de kilogramo : ergo, en cualquier unidad, la capacidad calorífica específica del agua es aproximadamente 1.

Base física

La temperatura de una muestra de una sustancia refleja la energía cinética promedio de sus partículas constituyentes (átomos o moléculas) en relación con su centro de masa. Sin embargo, no toda la energía proporcionada a una muestra de una sustancia se destinará a aumentar su temperatura, como lo demuestra el teorema de equipartición .

Gases monoatómicos

La mecánica cuántica predice que, a temperatura ambiente y a presiones ordinarias, un átomo aislado en un gas no puede almacenar ninguna cantidad significativa de energía excepto en forma de energía cinética. Por lo tanto, la capacidad calorífica por mol es la misma para todos los gases monoatómicos (como los gases nobles). Más precisamente, y , donde es la unidad de gas ideal (que es el producto de la constante de conversión de Boltzmann de la unidad de energía microscópica kelvin a la unidad de energía macroscópica joule , y el número de Avogadro ). ${\displaystyle c_{V,\mathrm {m} }=3R/2\approx \mathrm {12.5\,J\cdot K^{-1}\cdot mol^{-1}} }$ ${\displaystyle c_{P,\mathrm {m} }=5R/2\approx \mathrm {21\,J\cdot K^{-1}\cdot mol^{-1}} }$ ${\displaystyle R\approx \mathrm {8.31446\,J\cdot K^{-1}\cdot mol^{-1}} }$

Por lo tanto, la capacidad calorífica específica (por gramo, no por mol) de un gas monoatómico será inversamente proporcional a su peso atómico (adimensional) . Es decir, aproximadamente, ${\displaystyle A}$

$${\displaystyle c_{V}\approx \mathrm {12470\,J\cdot K^{-1}\cdot kg^{-1}} /A\quad \quad \quad c_{p}\approx \mathrm {20785\,J\cdot K^{-1}\cdot kg^{-1}} /A}$$

Para los gases nobles, desde el helio hasta el xenón, estos valores calculados son

Gases poliatomicos

Por otra parte, una molécula de gas poliatómico (formada por dos o más átomos unidos entre sí) puede almacenar energía térmica en forma de energía cinética, pero también en rotación de la molécula y vibración de los átomos entre sí (incluida la energía potencial interna ).

Estos grados de libertad adicionales o "modos" contribuyen a la capacidad calorífica específica de la sustancia. Es decir, cuando se inyecta energía térmica en un gas con moléculas poliatómicas, sólo una parte de ella se destinará a aumentar su energía cinética y, por lo tanto, la temperatura; el resto se destinará a los otros grados de libertad. Para lograr el mismo aumento de temperatura, se necesita más energía térmica para un gramo de esa sustancia que para un gramo de un gas monoatómico. Por lo tanto, la capacidad calorífica específica por mol de un gas poliatómico depende tanto de la masa molecular como del número de grados de libertad de las moléculas. ^{[23] [24] [25]}

La mecánica cuántica también afirma que cada modo rotacional o vibracional solo puede absorber o perder energía en ciertas cantidades discretas (cuantos). Dependiendo de la temperatura, la energía térmica promedio por molécula puede ser demasiado pequeña en comparación con los cuantos necesarios para activar algunos de esos grados de libertad. Se dice que esos modos están "congelados". En ese caso, la capacidad calorífica específica de la sustancia aumenta con la temperatura, a veces de manera gradual a medida que el modo se descongela y comienza a absorber parte de la energía térmica de entrada.

Por ejemplo, la capacidad calorífica molar del nitrógeno N
₂a volumen constante es (a 15 °C, 1 atm), que es . ^[26] Ese es el valor esperado de la teoría si cada molécula tuviera 5 grados de libertad. Estos resultan ser tres grados del vector de velocidad de la molécula, más dos grados de su rotación alrededor de un eje que pasa por el centro de masas y es perpendicular a la línea de los dos átomos. Debido a esos dos grados de libertad adicionales, la capacidad calorífica específica de N ${\displaystyle c_{V,\mathrm {m} }=\mathrm {20.6\,J\cdot K^{-1}\cdot mol^{-1}} }$ ${\displaystyle 2.49R}$ ${\displaystyle c_{V}}$
₂(736 J⋅K ⁻¹ ⋅kg ⁻¹ ) es mayor que la de un gas monatómico hipotético con la misma masa molecular 28 (445 J⋅K ⁻¹ ⋅kg ⁻¹ ), por un factor de ⁠5/3⁠ .

Este valor de la capacidad calorífica específica del nitrógeno es prácticamente constante desde menos de -150 °C hasta aproximadamente 300 °C. En ese rango de temperatura, los dos grados de libertad adicionales que corresponden a las vibraciones de los átomos, que estiran y comprimen el enlace, todavía están "congelados". Aproximadamente a esa temperatura, esos modos comienzan a "descongelarse" y, como resultado, comienzan a aumentar rápidamente al principio, luego más lentamente a medida que tienden a otro valor constante. Es 35,5 J⋅K ⁻¹ ⋅mol ⁻¹ a 1500 °C, 36,9 a 2500 °C y 37,5 a 3500 °C. ^[27] El último valor corresponde casi exactamente al valor predicho para 7 grados de libertad por molécula. ${\displaystyle c_{V}}$

Derivaciones de la capacidad calorífica

Relación entre capacidades caloríficas específicas

A partir de la relación termodinámica fundamental se puede demostrar,

$${\displaystyle c_{p}-c_{v}={\frac {\alpha ^{2}T}{\rho \beta _{T}}}}$$

dónde

• ${\displaystyle \alpha }$es el coeficiente de expansión térmica ,
• ${\displaystyle \beta _{T}}$es la compresibilidad isotérmica , y
• ${\displaystyle \rho }$es densidad​

En el artículo Relaciones entre calores específicos se analiza una derivación .

Para un gas ideal , si se expresa como densidad molar en la ecuación anterior, esta ecuación se reduce simplemente a la relación de Mayer , ${\displaystyle \rho }$

$${\displaystyle C_{p,m}-C_{v,m}=R\!}$$

donde y son capacidades caloríficas de propiedad intensiva expresadas en términos por mol a presión constante y volumen constante, respectivamente. ${\displaystyle C_{p,m}}$ ${\displaystyle C_{v,m}}$

Capacidad calorífica específica

La capacidad calorífica específica de un material en términos de masa es

$${\displaystyle c={\partial C \over \partial m},}$$

que en ausencia de transiciones de fase es equivalente a

$${\displaystyle c=E_{m}={C \over m}={C \over {\rho V}},}$$

dónde

• ${\displaystyle C}$es la capacidad calorífica de un cuerpo hecho del material en cuestión,
• ${\displaystyle m}$es la masa del cuerpo,
• ${\displaystyle V}$es el volumen del cuerpo, y
• ${\displaystyle \rho ={\frac {m}{V}}}$es la densidad del material.

En el caso de los gases, y también de otros materiales sometidos a altas presiones, es necesario distinguir entre diferentes condiciones límite para los procesos en consideración (ya que los valores difieren significativamente entre diferentes condiciones). Los procesos típicos para los que se puede definir una capacidad térmica incluyen procesos isobáricos (presión constante, ) o isocóricos (volumen constante, ). Las capacidades térmicas específicas correspondientes se expresan como ${\displaystyle dp=0}$ ${\displaystyle dV=0}$

$${\displaystyle {\begin{aligned}c_{p}&=\left({\frac {\partial C}{\partial m}}\right)_{p},\\c_{V}&=\left({\frac {\partial C}{\partial m}}\right)_{V}.\end{aligned}}}$$

Un parámetro relacionado con es , la capacidad calorífica volumétrica . En la práctica de ingeniería, para sólidos o líquidos a menudo significa una capacidad calorífica volumétrica, en lugar de una de volumen constante. En tales casos, la capacidad calorífica específica de la masa a menudo se escribe explícitamente con el subíndice , como . Por supuesto, a partir de las relaciones anteriores, para sólidos se escribe ${\displaystyle c}$ ${\displaystyle CV^{-1}}$ ${\displaystyle c_{V}}$ ${\displaystyle m}$ ${\displaystyle c_{m}}$

$${\displaystyle c_{m}={\frac {C}{m}}={\frac {c_{V}}{\rho }}.}$$

Para compuestos químicos homogéneos puros con masa molecular o molar establecida o una cantidad molar establecida, la capacidad calorífica como propiedad intensiva se puede expresar en base a mol en lugar de en base a masa mediante las siguientes ecuaciones análogas a las ecuaciones por masa:

$${\displaystyle {\begin{alignedat}{3}C_{p,m}=\left({\frac {\partial C}{\partial n}}\right)_{p}&={\text{molar heat capacity at constant pressure}}\\C_{V,m}=\left({\frac {\partial C}{\partial n}}\right)_{V}&={\text{molar heat capacity at constant volume}}\end{alignedat}}}$$

donde n = número de moles en el cuerpo o sistema termodinámico . Se puede hacer referencia a esta cantidad por mol como capacidad calorífica molar para distinguirla de la capacidad calorífica específica sobre una base por masa.

Capacidad calorífica politrópica

La capacidad calorífica politrópica se calcula en procesos si cambian todas las propiedades termodinámicas (presión, volumen, temperatura).

$${\displaystyle C_{i,m}=\left({\frac {\partial C}{\partial n}}\right)={\text{molar heat capacity at polytropic process}}}$$

Los procesos politrópicos más importantes ocurren entre las funciones adiabática e isoterma, el índice politrópico está entre 1 y el exponente adiabático ( γ o κ ).

Capacidad calorífica adimensional

La capacidad calorífica adimensional de un material es

$${\displaystyle C^{*}={\frac {C}{nR}}={\frac {C}{Nk_{\text{B}}}}}$$

dónde

• C es la capacidad calorífica de un cuerpo hecho del material en cuestión (J/K)
• n es la cantidad de sustancia en el cuerpo ( mol )
• R es la constante del gas (J⋅K ⁻¹ ⋅mol ⁻¹ )
• N es el número de moléculas en el cuerpo. (adimensional)
• k _B es la constante de Boltzmann (J⋅K ⁻¹ )

Nuevamente se muestran las unidades del SI como ejemplo.

Lea más sobre las cantidades de dimensión uno ^[28] en BIPM

En el artículo sobre gas ideal , la capacidad calorífica adimensional se expresa como . ${\displaystyle C^{*}}$ ${\displaystyle {\hat {c}}}$

Capacidad calorífica en el cero absoluto

De la definición de entropía

$${\displaystyle TdS=\delta Q}$$

La entropía absoluta se puede calcular integrando desde la temperatura de cero kelvin hasta la temperatura final T _f

$${\displaystyle S(T_{f})=\int _{T=0}^{T_{f}}{\frac {\delta Q}{T}}=\int _{0}^{T_{f}}{\frac {\delta Q}{dT}}{\frac {dT}{T}}=\int _{0}^{T_{f}}C(T)\,{\frac {dT}{T}}.}$$

La capacidad calorífica debe ser cero a temperatura cero para que la integral anterior no produzca una entropía absoluta infinita, violando así la tercera ley de la termodinámica . Una de las fortalezas del modelo de Debye es que (a diferencia del modelo de Einstein anterior) predice la forma matemática adecuada de la aproximación de la capacidad calorífica hacia cero, a medida que se acerca a la temperatura del cero absoluto.

Fase sólida

La capacidad calorífica máxima teórica para gases multiatómicos cada vez más grandes a temperaturas más altas también se acerca al límite de Dulong-Petit de 3 R , siempre que se calcule por mol de átomos, no de moléculas. La razón es que los gases con moléculas muy grandes, en teoría, tienen casi la misma capacidad calorífica a alta temperatura que los sólidos, y solo les falta la (pequeña) contribución de capacidad calorífica que proviene de la energía potencial que no se puede almacenar entre moléculas separadas en un gas.

El límite de Dulong-Petit resulta del teorema de equipartición y, como tal, solo es válido en el límite clásico de un continuo de microestados, que es un límite de alta temperatura. Para los elementos ligeros y no metálicos, así como para la mayoría de los sólidos moleculares comunes basados ​​en compuestos de carbono a temperatura ambiente estándar , los efectos cuánticos también pueden desempeñar un papel importante, como lo hacen en los gases multiatómicos. Estos efectos generalmente se combinan para dar capacidades térmicas inferiores a 3 R por mol de átomos en el sólido, aunque en los sólidos moleculares, las capacidades térmicas calculadas por mol de moléculas en los sólidos moleculares pueden ser superiores a 3 R. Por ejemplo, la capacidad térmica del hielo de agua en el punto de fusión es de aproximadamente 4,6 R por mol de moléculas, pero solo 1,5 R por mol de átomos. El número inferior a 3 R "por átomo" (como es el caso del diamante y el berilio) resulta de la "congelación" de los posibles modos de vibración para átomos ligeros a temperaturas adecuadamente bajas, al igual que en muchos gases de átomos de baja masa a temperatura ambiente. Debido a las altas energías de enlace de los cristales, estos efectos se observan en sólidos con más frecuencia que en líquidos: por ejemplo, la capacidad calorífica del agua líquida es el doble de la del hielo a casi la misma temperatura, y nuevamente está cerca de los 3 R por mol de átomos del máximo teórico de Dulong-Petit.

Para un análisis más moderno y preciso de las capacidades térmicas de los sólidos, especialmente a bajas temperaturas, es útil utilizar la idea de fonones . Véase el modelo de Debye .

Estimación teórica

El método de Monte Carlo de la integral de trayectorias es un enfoque numérico para determinar los valores de la capacidad térmica, basado en principios dinámicos cuánticos. Sin embargo, se pueden hacer buenas aproximaciones para gases en muchos estados utilizando métodos más simples que se describen a continuación. Para muchos sólidos compuestos de átomos relativamente pesados ​​(número atómico > hierro), a temperaturas no criogénicas, la capacidad térmica a temperatura ambiente se acerca a 3R = 24,94 julios por kelvin por mol de átomos (ley de Dulong-Petit, R es la constante de los gases). Se pueden hacer aproximaciones de baja temperatura para gases y sólidos a temperaturas inferiores a sus temperaturas características de Einstein o Debye mediante los métodos de Einstein y Debye que se describen a continuación.

• Agua (líquido): CP = 4185,5 J⋅K ⁻¹ ⋅kg ⁻¹ (15 °C, 101,325 kPa)
• Agua (líquido): CVH = 74,539 J⋅K ⁻¹ ⋅mol ⁻¹ (25 °C)

En el caso de líquidos y gases, es importante conocer la presión a la que se refieren los datos de capacidad térmica. La mayoría de los datos publicados se dan para la presión estándar. Sin embargo, diferentes organizaciones han definido diferentes condiciones estándar para la temperatura y la presión. La Unión Internacional de Química Pura y Aplicada (IUPAC) cambió su recomendación de una atmósfera al valor redondo de 100 kPa (≈750,062 Torr). ^{[notas 1]}

Relación entre capacidades térmicas

Medir la capacidad calorífica específica a volumen constante puede resultar prohibitivamente difícil para líquidos y sólidos. Es decir, pequeños cambios de temperatura suelen requerir grandes presiones para mantener un líquido o sólido a volumen constante, lo que implica que el recipiente que lo contiene debe ser casi rígido o al menos muy fuerte (véase coeficiente de expansión térmica y compresibilidad ). En cambio, es más fácil medir la capacidad calorífica a presión constante (permitiendo que el material se expanda o contraiga libremente) y calcular la capacidad calorífica a volumen constante utilizando relaciones matemáticas derivadas de las leyes termodinámicas básicas.

El índice de capacidad térmica , o índice adiabático, es la relación entre la capacidad térmica a presión constante y la capacidad térmica a volumen constante. A veces también se lo conoce como factor de expansión isentrópica.

Gas ideal

Para un gas ideal , evaluando las derivadas parciales anteriores de acuerdo con la ecuación de estado , donde R es la constante del gas , para un gas ideal ^[29]

$${\displaystyle {\begin{alignedat}{3}PV&=nRT,&\\C_{P}-C_{V}&=T\left({\frac {\partial P}{\partial T}}\right)_{V,n}\left({\frac {\partial V}{\partial T}}\right)_{P,n},&\\P&={\frac {nRT}{V}}\Rightarrow \left({\frac {\partial P}{\partial T}}\right)_{V,n}&={\frac {nR}{V}},\\V&={\frac {nRT}{P}}\Rightarrow \left({\frac {\partial V}{\partial T}}\right)_{P,n}&={\frac {nR}{P}}.\end{alignedat}}}$$

Sustituyendo

$${\displaystyle T\left({\frac {\partial P}{\partial T}}\right)_{V,n}\left({\frac {\partial V}{\partial T}}\right)_{P,n}=T{\frac {nR}{V}}{\frac {nR}{P}}={\frac {nRT}{V}}{\frac {nR}{P}}=P{\frac {nR}{P}}=nR,}$$

Esta ecuación se reduce simplemente a la relación de Mayer :

$${\displaystyle C_{P,m}-C_{V,m}=R.}$$

Las diferencias en las capacidades térmicas definidas por la relación de Mayer anterior sólo son exactas para un gas ideal y serían diferentes para cualquier gas real.

Capacidad calorífica específica

La capacidad calorífica específica de un material en términos de masa es

$${\displaystyle c={\frac {\partial C}{\partial m}},}$$

que en ausencia de transiciones de fase es equivalente a

$${\displaystyle c=E_{m}={\frac {C}{m}}={\frac {C}{\rho V}},}$$

dónde

• ${\displaystyle C}$es la capacidad calorífica de un cuerpo hecho del material en cuestión,
• ${\displaystyle m}$es la masa del cuerpo,
• ${\displaystyle V}$es el volumen del cuerpo,
• ${\displaystyle \rho ={\frac {m}{V}}}$es la densidad del material.

En el caso de los gases, y también de otros materiales sometidos a altas presiones, es necesario distinguir entre diferentes condiciones límite para los procesos en consideración (ya que los valores difieren significativamente entre diferentes condiciones). Los procesos típicos para los que se puede definir una capacidad térmica incluyen procesos isobáricos (presión constante, ) o isocóricos (volumen constante, ). Las capacidades térmicas específicas correspondientes se expresan como ${\displaystyle {\text{d}}P=0}$ ${\displaystyle {\text{d}}V=0}$

$${\displaystyle {\begin{aligned}c_{P}&=\left({\frac {\partial C}{\partial m}}\right)_{P},\\c_{V}&=\left({\frac {\partial C}{\partial m}}\right)_{V}.\end{aligned}}}$$

A partir de los resultados de la sección anterior, dividiendo por la masa se obtiene la relación

$${\displaystyle c_{P}-c_{V}={\frac {\alpha ^{2}T}{\rho \beta _{T}}}.}$$

Un parámetro relacionado con es , la capacidad calorífica volumétrica . En la práctica de ingeniería, para sólidos o líquidos a menudo significa una capacidad calorífica volumétrica, en lugar de una de volumen constante. En tales casos, la capacidad calorífica específica a menudo se escribe explícitamente con el subíndice , como . Por supuesto, a partir de las relaciones anteriores, para sólidos se escribe ${\displaystyle c}$ ${\displaystyle C/V}$ ${\displaystyle c_{V}}$ ${\displaystyle m}$ ${\displaystyle c_{m}}$

$${\displaystyle c_{m}={\frac {C}{m}}={\frac {c_{\text{volumetric}}}{\rho }}.}$$

Para compuestos químicos homogéneos puros con una masa molecular o molar establecida , o una cantidad molar , la capacidad calorífica como propiedad intensiva se puede expresar en base a mol en lugar de masa mediante las siguientes ecuaciones análogas a las ecuaciones por masa:

$${\displaystyle {\begin{alignedat}{3}C_{P,m}&=\left({\frac {\partial C}{\partial n}}\right)_{P}&={\text{molar heat capacity at constant pressure,}}\\C_{V,m}&=\left({\frac {\partial C}{\partial n}}\right)_{V}&={\text{molar heat capacity at constant volume,}}\end{alignedat}}}$$

donde n es el número de moles en el cuerpo o sistema termodinámico . Se puede hacer referencia a esta cantidad por mol como capacidad calorífica molar para distinguirla de la capacidad calorífica específica sobre una base por masa.

Capacidad calorífica politrópica

La capacidad térmica politrópica se calcula en procesos en los que cambian todas las propiedades termodinámicas (presión, volumen, temperatura):

$${\displaystyle C_{i,m}=\left({\frac {\partial C}{\partial n}}\right)={\text{molar heat capacity at polytropic process.}}}$$

Los procesos politrópicos más importantes ocurren entre las funciones adiabática e isoterma, el índice politrópico está entre 1 y el exponente adiabático ( γ o κ ).

Capacidad calorífica adimensional

La capacidad calorífica adimensional de un material es

$${\displaystyle C^{*}={\frac {C}{nR}}={\frac {C}{Nk_{\text{B}}}},}$$

dónde

• ${\displaystyle C}$es la capacidad calorífica de un cuerpo hecho del material en cuestión (J/K),
• n es la cantidad de sustancia en el cuerpo ( mol ),
• R es la constante del gas (J/(K⋅mol)),
• N es el número de moléculas en el cuerpo (adimensional),
• k _B es la constante de Boltzmann (J/(K⋅molécula)).

En el artículo sobre los gases ideales , la capacidad calorífica adimensional se expresa como y está relacionada directamente con la mitad del número de grados de libertad por partícula. Esto es válido para los grados de libertad cuadráticos, una consecuencia del teorema de equipartición . ${\displaystyle C^{*}}$ ${\displaystyle {\hat {c}}}$

De manera más general, la capacidad térmica adimensional relaciona el aumento logarítmico de la temperatura con el aumento de la entropía adimensional por partícula , medida en nats . ${\displaystyle S^{*}=S/Nk_{\text{B}}}$

$${\displaystyle C^{*}={\frac {{\text{d}}S^{*}}{{\text{d}}(\ln T)}}.}$$

Alternativamente, utilizando logaritmos de base 2, se relaciona el aumento logarítmico de base 2 en la temperatura con el aumento de la entropía adimensional medida en bits . ^[30] ${\displaystyle C^{*}}$

Capacidad calorífica en el cero absoluto

De la definición de entropía

$${\displaystyle T\,{\text{d}}S=\delta Q,}$$

La entropía absoluta se puede calcular integrando desde cero hasta la temperatura final T _f :

$${\displaystyle S(T_{\text{f}})=\int _{T=0}^{T_{\text{f}}}{\frac {\delta Q}{T}}=\int _{0}^{T_{\text{f}}}{\frac {\delta Q}{{\text{d}}T}}{\frac {{\text{d}}T}{T}}=\int _{0}^{T_{\text{f}}}C(T)\,{\frac {{\text{d}}T}{T}}.}$$

Derivación termodinámica

En teoría, la capacidad calorífica específica de una sustancia también puede derivarse de su modelado termodinámico abstracto mediante una ecuación de estado y una función de energía interna.

Estado de la materia en una muestra homogénea

Para aplicar la teoría, se considera la muestra de la sustancia (sólida, líquida o gaseosa) para la cual se puede definir la capacidad calorífica específica; en particular, que tiene composición homogénea y masa fija . Supóngase que la evolución del sistema es siempre lo suficientemente lenta como para que la presión y la temperatura internas se consideren uniformes en todo su interior. La presión sería igual a la presión que le aplica el recinto o algún fluido circundante, como el aire. ${\displaystyle M}$ ${\displaystyle P}$ ${\displaystyle T}$ ${\displaystyle P}$

El estado del material puede entonces especificarse mediante tres parámetros: su temperatura , la presión y su volumen específico , donde es el volumen de la muestra. (Esta cantidad es el recíproco de la densidad del material ). Al igual que y , el volumen específico es una propiedad intensiva del material y su estado, que no depende de la cantidad de sustancia en la muestra. ${\displaystyle T}$ ${\displaystyle P}$ ${\displaystyle \nu =V/M}$ ${\displaystyle V}$ ${\displaystyle 1/\rho }$ ${\displaystyle \rho =M/V}$ ${\displaystyle T}$ ${\displaystyle P}$ ${\displaystyle \nu }$

Estas variables no son independientes. Los estados permitidos se definen mediante una ecuación de estado que relaciona estas tres variables: La función depende del material en consideración. La energía interna específica almacenada internamente en la muestra, por unidad de masa, será entonces otra función de estas variables de estado, que también es específica del material. La energía interna total en la muestra será entonces . ${\displaystyle F(T,P,\nu )=0.}$ ${\displaystyle F}$ ${\displaystyle U(T,P,\nu )}$ ${\displaystyle M\,U(T,P,\nu )}$

Para algunos materiales simples, como un gas ideal , se puede derivar de la teoría básica la ecuación de estado e incluso la energía interna específica. En general, estas funciones deben determinarse experimentalmente para cada sustancia. ${\displaystyle F=0}$ ${\displaystyle U}$

Conservación de energía

El valor absoluto de esta cantidad no está definido y (para los fines de la termodinámica) el estado de "energía interna cero" puede elegirse arbitrariamente. Sin embargo, por la ley de conservación de la energía , cualquier aumento infinitesimal en la energía interna total debe ser igualado por el flujo neto de energía térmica hacia la muestra, más cualquier energía mecánica neta proporcionada a la misma por el recinto o medio circundante sobre ella. Este último es , donde es el cambio en el volumen de la muestra en ese paso infinitesimal. ^[31] Por lo tanto ${\displaystyle M\,\mathrm {d} U}$ ${\displaystyle MU}$ ${\displaystyle \mathrm {d} Q}$ ${\displaystyle -P\,\mathrm {d} V}$ ${\displaystyle \mathrm {d} V}$

$${\displaystyle \mathrm {d} Q-P\,\mathrm {d} V=M\,\mathrm {d} U}$$

por eso

$${\displaystyle {\frac {\mathrm {d} Q}{M}}-P\,\mathrm {d} \nu =\mathrm {d} U}$$

Si el volumen de la muestra (y por lo tanto el volumen específico del material) se mantiene constante durante la inyección de la cantidad de calor , entonces el término es cero (no se realiza trabajo mecánico). Luego, dividiendo por , ${\displaystyle \mathrm {d} Q}$ ${\displaystyle P\,\mathrm {d} \nu }$ ${\displaystyle \mathrm {d} T}$

$${\displaystyle {\frac {\mathrm {d} Q}{M\,\mathrm {d} T}}={\frac {\mathrm {d} U}{\mathrm {d} T}}}$$

donde es el cambio de temperatura que resulta del aporte de calor. El lado izquierdo es la capacidad calorífica específica a volumen constante del material. ${\displaystyle \mathrm {d} T}$ ${\displaystyle c_{V}}$

Para la capacidad térmica a presión constante, es útil definir la entalpía específica del sistema como la suma . Un cambio infinitesimal en la entalpía específica será entonces ${\displaystyle h(T,P,\nu )=U(T,P,\nu )+P\nu }$

$${\displaystyle \mathrm {d} h=\mathrm {d} U+V\,\mathrm {d} P+P\,\mathrm {d} V}$$

por lo tanto

$${\displaystyle {\frac {\mathrm {d} Q}{M}}+V\,\mathrm {d} P=\mathrm {d} h}$$

Si la presión se mantiene constante, el segundo término del lado izquierdo es cero, y

$${\displaystyle {\frac {\mathrm {d} Q}{M\,\mathrm {d} T}}={\frac {\mathrm {d} h}{\mathrm {d} T}}}$$

El lado izquierdo es la capacidad calorífica específica a presión constante del material. ${\displaystyle c_{P}}$

Conexión con la ecuación de estado

En general, las cantidades infinitesimales están limitadas por la ecuación de estado y la función de energía interna específica. Es decir, ${\displaystyle \mathrm {d} T,\mathrm {d} P,\mathrm {d} V,\mathrm {d} U}$

$${\displaystyle {\begin{cases}\displaystyle \mathrm {d} T{\frac {\partial F}{\partial T}}(T,P,V)+\mathrm {d} P{\frac {\partial F}{\partial P}}(T,P,V)+\mathrm {d} V{\frac {\partial F}{\partial V}}(T,P,V)&=&0\\[2ex]\displaystyle \mathrm {d} T{\frac {\partial U}{\partial T}}(T,P,V)+\mathrm {d} P{\frac {\partial U}{\partial P}}(T,P,V)+\mathrm {d} V{\frac {\partial U}{\partial V}}(T,P,V)&=&\mathrm {d} U\end{cases}}}$$

Aquí se denota la derivada (parcial) de la ecuación de estado con respecto a su argumento, manteniendo los otros dos argumentos fijos, evaluados en el estado en cuestión. Las otras derivadas parciales se definen de la misma manera. Estas dos ecuaciones en los cuatro incrementos infinitesimales normalmente las limitan a un subespacio lineal bidimensional de posibles cambios infinitesimales de estado, que depende del material y del estado. Los cambios a volumen constante y a presión constante son solo dos direcciones particulares en este espacio. ${\displaystyle (\partial F/\partial T)(T,P,V)}$ ${\displaystyle F}$ ${\displaystyle T}$ ${\displaystyle (T,P,V)}$

Este análisis también es válido independientemente de cómo se inyecte el incremento de energía en la muestra, es decir, por conducción de calor , irradiación, inducción electromagnética , desintegración radiactiva , etc. ${\displaystyle \mathrm {d} Q}$

Relación entre capacidades térmicas

Para cualquier volumen específico , denote la función que describe cómo varía la presión con la temperatura , como lo permite la ecuación de estado, cuando el volumen específico del material se mantiene constante a la fuerza en . Análogamente, para cualquier presión , sea la función que describe cómo varía el volumen específico con la temperatura, cuando la presión se mantiene constante en . Es decir, esas funciones son tales que ${\displaystyle \nu }$ ${\displaystyle p_{\nu }(T)}$ ${\displaystyle T}$ ${\displaystyle \nu }$ ${\displaystyle P}$ ${\displaystyle \nu _{P}(T)}$ ${\displaystyle P}$

$${\displaystyle F(T,p_{\nu }(T),\nu )=0}$$y $${\displaystyle F(T,P,\nu _{P}(T))=0}$$

para cualquier valor de . En otras palabras, los gráficos de y son cortes de la superficie definida por la ecuación de estado, cortados por planos de constante y constante , respectivamente. ${\displaystyle T,P,\nu }$ ${\displaystyle p_{\nu }(T)}$ ${\displaystyle \nu _{P}(T)}$ ${\displaystyle \nu }$ ${\displaystyle P}$

Entonces, de la relación termodinámica fundamental se deduce que

$${\displaystyle c_{P}(T,P,\nu )-c_{V}(T,P,\nu )=T\left[{\frac {\mathrm {d} p_{\nu }}{\mathrm {d} T}}(T)\right]\left[{\frac {\mathrm {d} \nu _{P}}{\mathrm {d} T}}(T)\right]}$$

Esta ecuación se puede reescribir como

$${\displaystyle c_{P}(T,P,\nu )-c_{V}(T,P,\nu )=\nu T{\frac {\alpha ^{2}}{\beta _{T}}},}$$

dónde

• ${\displaystyle \alpha }$es el coeficiente de expansión térmica ,
• ${\displaystyle \beta _{T}}$es la compresibilidad isotérmica ,

ambos dependiendo del estado . ${\displaystyle (T,P,\nu )}$

El índice de capacidad térmica , o índice adiabático, es la relación entre la capacidad térmica a presión constante y la capacidad térmica a volumen constante. A veces también se lo conoce como factor de expansión isentrópica. ${\displaystyle c_{P}/c_{V}}$

Cálculo a partir de primeros principios

El método de Monte Carlo de la integral de trayectorias es un enfoque numérico para determinar los valores de la capacidad térmica, basado en principios dinámicos cuánticos. Sin embargo, se pueden hacer buenas aproximaciones para gases en muchos estados utilizando métodos más simples que se describen a continuación. Para muchos sólidos compuestos de átomos relativamente pesados ​​(número atómico > hierro), a temperaturas no criogénicas, la capacidad térmica a temperatura ambiente se acerca a 3 R = 24,94 julios por kelvin por mol de átomos ( ley de Dulong-Petit , R es la constante de los gases ). Se pueden hacer aproximaciones de baja temperatura para gases y sólidos a temperaturas inferiores a sus temperaturas características de Einstein o temperaturas de Debye mediante los métodos de Einstein y Debye que se analizan a continuación. Sin embargo, se debe prestar atención a la coherencia de dichas consideraciones ab-initio cuando se utilizan junto con una ecuación de estado para el material considerado. ^[32]

Gas ideal

Para un gas ideal , evaluando las derivadas parciales anteriores de acuerdo con la ecuación de estado , donde R es la constante del gas , para un gas ideal ^[33]

${\displaystyle {\begin{alignedat}{3}PV&=nRT,\\C_{P}-C_{V}&=T\left({\frac {\partial P}{\partial T}}\right)_{V,n}\left({\frac {\partial V}{\partial T}}\right)_{P,n},\\P&={\frac {nRT}{V}}\Rightarrow \left({\frac {\partial P}{\partial T}}\right)_{V,n}&={\frac {nR}{V}},\\V&={\frac {nRT}{P}}\Rightarrow \left({\frac {\partial V}{\partial T}}\right)_{P,n}&={\frac {nR}{P}}.\end{alignedat}}}$

Sustituyendo

$${\displaystyle T\left({\frac {\partial P}{\partial T}}\right)_{V,n}\left({\frac {\partial V}{\partial T}}\right)_{P,n}=T{\frac {nR}{V}}{\frac {nR}{P}}={\frac {nRT}{V}}{\frac {nR}{P}}=P{\frac {nR}{P}}=nR,}$$

Esta ecuación se reduce simplemente a la relación de Mayer :

$${\displaystyle C_{P,m}-C_{V,m}=R.}$$

Las diferencias en las capacidades térmicas definidas por la relación de Mayer anterior sólo son exactas para un gas ideal y serían diferentes para cualquier gas real.

Véase también

Portal de física

• Calor específico de fusión (Entalpía de fusión)
• Calor específico de vaporización (Entalpía de vaporización)
• Línea de Frenkel
• Relación de capacidad calorífica
• Ecuación del calor
• Coeficiente de transferencia de calor
• Historia de la termodinámica
• Método de Joback (Estimación de capacidades térmicas)
• Calor latente
• Propiedades de los materiales (termodinámica)
• Mecánica estadística cuántica
• Valor R (aislamiento)
• Entalpía de vaporización
• Entalpía de fusión
• Mecánica estadística
• Tabla de capacidades caloríficas específicas
• Masa térmica
• Bases de datos termodinámicas para sustancias puras
• Ecuaciones termodinámicas
• Capacidad calorífica volumétrica

Notas

1. IUPAC , Compendio de terminología química , 2.ª ed. (el "Libro de oro") (1997). Versión corregida en línea: (2006–) "Presión estándar". doi :10.1351/goldbook.S05921.

Referencias

1. Halliday, David; Resnick, Robert; Walker, Jearl (2001). Fundamentos de física (6.ª ed.). Nueva York, NY, EE. UU.: John Wiley & Sons .
2. Open University (2008). S104 Libro 3 Energía y luz , pág. 59. The Open University . ISBN 9781848731646 . 
3. Open University (2008). S104 Libro 3 Energía y luz , pág. 179. The Open University . ISBN 9781848731646 . 
4. Engineering ToolBox (2003). "Calor específico de algunas sustancias comunes".
5. (2001): Columbia Encyclopedia , 6.ª ed.; citado por Encyclopedia.com. Columbia University Press. Consultado el 11 de abril de 2019.
6. Laidler, Keith J. (1993). El mundo de la química física. Oxford University Press. ISBN 0-19-855919-4.
7. Ramsay, William (1918). La vida y las cartas de Joseph Black, MD . Constable. págs. 38–39.
8. Black, Joseph (1807). Robison, John (ed.). Lecciones sobre los elementos de la química: dictadas en la Universidad de Edimburgo. Vol. 1. Mathew Carey. págs. 76–77.
9. West, John B. (15 de junio de 2014). "Joseph Black, dióxido de carbono, calor latente y los inicios del descubrimiento de los gases respiratorios". American Journal of Physiology-Lung Cellular and Molecular Physiology . 306 (12): L1057–L1063. doi :10.1152/ajplung.00020.2014. ISSN  1040-0605.
10. Oficina Internacional de Pesas y Medidas (2006), El Sistema Internacional de Unidades (SI) (PDF) (8.ª ed.), ISBN 92-822-2213-6, archivado (PDF) del original el 4 de junio de 2021 , consultado el 16 de diciembre de 2021
11. "Agua: propiedades térmicas". Engineeringtoolbox.com . Consultado el 29 de marzo de 2021 .
12. Unión Internacional de Química Pura y Aplicada, División de Química Física. "Cantidades, unidades y símbolos en química física" (PDF) . Blackwell Sciences. pág. 7. El adjetivo específico antes del nombre de una cantidad extensiva se usa a menudo para significar dividido por masa.
13. Sanal Kumar, realidad virtual; Sankar, Vigneshwaran; Chandrasekaran, Nichith; Saravanan, Vignesh; Sukumaran, Ajith; Rajendran, Vigneshwaran; Choudhary, Shiv Kumar; Radhakrishnan, Pradeep Kumar; Dios mío, Charlie; Panchal, Dhruv; Rafic, Sultán Ariff Rahman Mohamed; Bharat, Rajaghatta Sundararam; Raj, Yash; Shrivastava, Srajan (2022). "Datos de referencia universales del bloqueo de la capa límite tridimensional y el coeficiente de fricción promedio para la verificación del código in silico". Física de Fluidos . 34 (4): 041301. Código bibliográfico : 2022PhFl...34d1301S. doi :10.1063/5.0086638.
14. Sanal Kumar, realidad virtual; Sundararam, Bharath Rajaghatta; Radhakrishnan, Pradeep Kumar; Chandrasekaran, Nichith; Choudhary, Shiv Kumar; Sankar, Vigneshwaran; Sukumaran, Ajith; Rajendran, Vigneshwaran; Rafic, Sultán Ariff Rahman Mohamed; Panchal, Dhruv; Raj, Yash; Shrivastava, Srajan; Dios mío, Charlie; Jayaraman, Anbu; Rajamanickam, Deveswaran; Srinivasan, Bharat (2022). "Predicción in vitro del índice de asfixia del flujo de biofluido crítico inferior / superior y demostración in vivo de la asfixia del flujo en la arteria estenótica del animal con embolia gaseosa". Física de Fluidos . 34 (10). Código Bib : 2022PhFl...34j1302S. doi :10.1063/5.0105407.
15. Manual de química de Lange, 10ª ed., página 1524.
16. Quick, CR; Schawe, JEK; Uggowitzer, PJ; Pogatscher, S. (1 de julio de 2019). "Medición de la capacidad calorífica específica mediante calorimetría de barrido rápido: precisión y correcciones de pérdidas". Thermochimica Acta . Número especial con motivo del 65.º cumpleaños de Christoph Schick. 677 : 12–20. Bibcode :2019TcAc..677...12Q. doi : 10.1016/j.tca.2019.03.021 . ISSN  0040-6031.
17. Pogatscher, S.; Leutenegger, D.; Schawe, JEK; Uggowitzer, PJ; Löffler, JF (septiembre de 2016). "Transiciones de fase sólido-sólido mediante fusión de metales". Comunicaciones de la naturaleza . 7 (1): 11113. Código bibliográfico : 2016NatCo...711113P. doi : 10.1038/ncomms11113. ISSN  2041-1723. PMC 4844691 . PMID  27103085. 
18. Koch, Werner (2013). Tablas de vapor VDI (4.ª ed.). Springer. pág. 8. ISBN 9783642529412.Publicado bajo los auspicios de Verein Deutscher Ingenieure (VDI).
19. Cardarelli, Francois (2012). Conversión de unidades científicas: una guía práctica para el sistema métrico. MJ Shields (traducción) (2.ª ed.). Springer. pág. 19. ISBN 9781447108054.
20. De valores directos: 1 ⁠BTU/lb⋅°R× 1055.06​Yo/BTU× ( ⁠1/0,45359237⁠ ) ​​⁠libra/kilogramo⁠ x ⁠9/5⁠ ⁠° R/K⁠ = 4186,82 ⁠Yo/kg⋅K⁠
21. °F=°R
22. °C=K
23. Feynman, R., Las conferencias Feynman sobre física , vol. 1, cap. 40, págs. 7-8
24. Reif, F. (1965). Fundamentos de física estadística y térmica . McGraw-Hill. págs. 253–254.
25. Kittel, Charles; Kroemer, Herbert (2000). Física térmica . WH Freeman. pág. 78. ISBN 978-0-7167-1088-2.
26. Thornton, Steven T. y Rex, Andrew (1993) Física moderna para científicos e ingenieros , Saunders College Publishing
27. Chase, MW Jr. (1998) Tablas termoquímicas NIST-JANAF, cuarta edición , en Journal of Physical and Chemical Reference Data , monografía 9, páginas 1–1951.
28. "Acerca de la unidad uno".
29. Yunus A. Cengel y Michael A. Boles, Termodinámica: un enfoque de ingeniería , 7.ª edición, McGraw-Hill, 2010, ISBN 007-352932-X . 
30. Fraundorf, P. (2003). "Capacidad calorífica en bits". American Journal of Physics . 71 (11): 1142. arXiv : cond-mat/9711074 . Código Bibliográfico :2003AmJPh..71.1142F. doi :10.1119/1.1593658. S2CID  18742525.
31. Feynman, Richard, Las conferencias Feynman sobre física , vol. 1, cap. 45
32. S. Benjelloun, "Identidades termodinámicas y consistencia termodinámica de la ecuación de estados", Enlace a la impresión electrónica de archivo Enlace a la impresión electrónica de Hal
33. Cengel, Yunus A. y Boles, Michael A. (2010) Termodinámica: un enfoque de ingeniería , 7.ª edición, McGraw-Hill ISBN 007-352932-X . 

Lectura adicional

• Emmerich Wilhelm y Trevor M. Letcher, Eds., 2010, Heat Capacities: Liquids, Solutions and Vapours , Cambridge, Reino Unido: Royal Society of Chemistry, ISBN 0-85404-176-1 . Un esquema muy reciente de aspectos tradicionales seleccionados del tema del título, incluida una introducción especializada reciente a su teoría, Emmerich Wilhelm, "Heat Capacities: Introduction, Concepts, and Selected Applications" (Capítulo 1, págs. 1-27), capítulos sobre métodos experimentales tradicionales y más contemporáneos como los métodos fotoacústicos , por ejemplo, Jan Thoen y Christ Glorieux, "Photothermal Techniques for Heat Capacities", y capítulos sobre nuevos intereses de investigación, incluidas las capacidades térmicas de las proteínas y otros sistemas poliméricos (Capítulos 16, 15), de cristales líquidos (Capítulo 17), etc. 

Enlaces externos

• (24 de mayo de 2012) La teoría de los fonones arroja luz sobre la termodinámica de los líquidos y la capacidad térmica – Physics World La teoría de los fonones en la termodinámica de los líquidos | Scientific Reports