La afinación de cinco límites , afinación de 5 límites , o afinación de 5 límites primos (no confundir con la afinación de 5 límites impares ), es cualquier sistema de afinación de un instrumento musical que obtiene la frecuencia de cada nota multiplicando la frecuencia. de una nota de referencia determinada (la nota base) por productos de potencias enteras de 2, 3 o 5 ( números primos limitados a 5 o menos), como 2 −3 ·3 1 ·5 1 = 15/8 .
Las potencias de 2 representan movimientos interválicos de octavas. Las potencias de 3 representan movimientos en intervalos de quintas perfectas (más una octava, que se puede eliminar multiplicando por 1/2, es decir, 2 −1 ). Las potencias de 5 representan intervalos de terceras mayores (más dos octavas, que se pueden eliminar multiplicando por 1/4, es decir, 2 −2 ). Por lo tanto, las afinaciones de 5 límites se construyen enteramente a partir del apilamiento de tres intervalos básicos puramente afinados (octavas, terceras y quintas). Dado que la percepción de consonancia parece estar relacionada con números bajos en la serie armónica, y la afinación de 5 límites se basa en los tres números primos más bajos, la afinación de 5 límites debería ser capaz de producir armonías muy consonantes. De ahí que la afinación de 5 límites se considere un método para obtener una entonación justa .
El número de intervalos potenciales, clases de tono, tonos, centros de clave, acordes y modulaciones disponibles para afinaciones de 5 límites es ilimitado, porque ninguna potencia (entero distinto de cero) de cualquier primo es igual a la potencia de cualquier otro primo, por lo que los intervalos disponibles pueden Se puede imaginar que se extiende indefinidamente en una red tridimensional (una dimensión, o una dirección, para cada primo). Si se ignoran las octavas, se puede ver como una red bidimensional de clases de tonos (nombres de notas) que se extiende indefinidamente en dos direcciones.
Sin embargo, la mayoría de los sistemas de afinación diseñados para instrumentos acústicos restringen el número total de tonos por razones prácticas. También es típico (pero no siempre es así) tener el mismo número de tonos en cada octava, lo que representa transposiciones de octava de un conjunto fijo de clases de tonos. En ese caso, el sistema de afinación también puede considerarse como una escala de repetición de octavas de un cierto número de tonos por octava.
La frecuencia de cualquier tono en un sistema de afinación de 5 límites particular se puede obtener multiplicando la frecuencia de un tono de referencia fijo elegido para el sistema de afinación (como A440 , A442, A432, C256, etc.) por alguna combinación de las potencias. de 3 y 5 para determinar la clase de tono y alguna potencia de 2 para determinar la octava.
Por ejemplo, si tenemos un sistema de afinación de 5 límites donde la nota base es C256 (lo que significa que tiene 256 ciclos por segundo y decidimos llamarla C), entonces f C = 256 Hz, o "la frecuencia de C es igual a 256 Hz". ". Hay varias formas de definir E por encima de esta C. Usando tercios, se puede subir un factor 5 y bajar dos factores 2, alcanzando una relación de frecuencia de 5/4, o usando quintos se puede subir cuatro factores de 3 y bajar seis. factores de 2, llegando a 81/64. Las frecuencias se convierten en:
o
Suponiendo que nos limitemos a siete clases de tono (siete notas por octava), es posible afinar la familiar escala diatónica usando la afinación de 5 límites de varias maneras, todas las cuales hacen que la mayoría de las tríadas estén idealmente afinadas y sean tan consonantes y estables. como sea posible, pero deje algunas tríadas en configuraciones interválicas menos estables.
Las notas prominentes de una escala determinada se afinan de modo que sus frecuencias formen proporciones de números enteros relativamente pequeños. Por ejemplo, en la tonalidad de sol mayor , la relación de las frecuencias de las notas sol a re (una quinta justa ) es 3/2, mientras que la de sol a do es 2/3 (una quinta justa descendente) o 4/ 3 (una cuarta perfecta ) subiendo, y la tercera mayor G a B es 5/4.

Se puede derivar una escala diatónica justa de la siguiente manera. Imaginando la tonalidad de do mayor, supongamos que insistimos en que la raíz subdominante fa y la raíz dominante sol estén a una quinta (3:2) de la raíz tónica do en cada lado, y que los acordes FAC, CEG y GBD sean solo mayores. tríadas (con relaciones de frecuencia 4:5:6):
Esto se conoce como escala diatónica intensa de Ptolomeo . Aquí, la fila titulada "Natural" expresa todas estas razones usando una lista común de números naturales (multiplicando la fila de arriba por el mcm de sus denominadores). En otras palabras, la aparición más baja de esta forma de escala de una octava dentro de la serie armónica es como un subconjunto de 7 de los 24 armónicos que se encuentran en la octava desde los armónicos 24 al 48.
Los tres tercios mayores son correctos (5:4), y tres de los tercios menores son como se esperaba (6:5), pero de re a fa es un semidítono o un tercio menor pitagórico (igual a tres quintas justas descendentes, ajustadas en octava). , una coma sintónica más estrecha que una tercera menor justamente afinada (6:5).
Como consecuencia, obtenemos una escala en la que EGB y ACE son sólo tríadas menores (10:12:15), pero la tríada DFA no tiene la forma ni el sonido menor que podríamos esperar, siendo (27:32:40) . Además, la tríada BDF no es la tríada disminuida (25:30:36) que obtendríamos al apilar dos terceras menores 6:5, siendo (45:54:64) en su lugar: [1] [2]
Se puede ver que aparecen intervalos de escala básicos por pasos:
que pueden combinarse para formar intervalos más grandes (entre otros):
Otra forma de hacerlo es la siguiente. Pensando en la tonalidad menor relativa de La menor y usando D, A y E como nuestra columna vertebral de quintas, podemos insistir en que los acordes DFA, ACE y EGB sean solo tríadas menores (10:12:15):
Si contrastamos eso con la escala anterior, vemos que para cinco pares de notas sucesivas las proporciones de los pasos siguen siendo las mismas, pero en una nota, D, los pasos CD y DE han cambiado sus proporciones.
Los tres tercios mayores siguen siendo 5:4, y tres de los tercios menores siguen siendo 6:5 y el cuarto es 32:27, excepto que ahora es BD en lugar de DF que es 32:27. FAC y CEG todavía forman tríadas principales (4:5:6), pero ahora GBD es (108:135:160) y BDF ahora (135:160:192).
Hay otras posibilidades como subir A en lugar de bajar D, pero cada ajuste rompe algo más.
Evidentemente no es posible obtener las siete tríadas diatónicas en la configuración (4:5:6) para mayor, (10:12:15) para menor y (25:30:36) para disminuida al mismo tiempo si limitarnos a siete lanzamientos.
Eso demuestra la necesidad de aumentar el número de tonos para ejecutar las armonías deseadas afinadas.
Para construir una escala de doce tonos en afinación de 5 límites, comenzamos construyendo una tabla que contiene quince tonos justamente entonados:
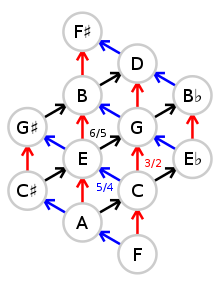
Los factores enumerados en la primera fila y la primera columna son potencias de 3 y 5 respectivamente (por ejemplo, 1 ⁄ 9 = 3 −2 ). Los colores indican parejas de notas enarmónicas con tono casi idéntico. Todas las proporciones se expresan en relación con C en el centro de este diagrama (la nota base de esta escala). Se calculan en dos pasos:
Tenga en cuenta que las potencias de 2 utilizadas en el segundo paso pueden interpretarse como octavas ascendentes o descendentes . Por ejemplo, multiplicar la frecuencia de una nota por 2 6 significa aumentarla en 6 octavas. Además, cada fila de la tabla puede considerarse una secuencia de quintas (ascendente hacia la derecha) y cada columna una secuencia de terceras mayores (ascendente hacia arriba). Por ejemplo, en la primera fila de la tabla, hay una quinta ascendente de D y A, y otra (seguida de una octava descendente) de A a E. Esto sugiere un método alternativo pero equivalente para calcular las mismas proporciones. Por ejemplo, puede obtener A (proporción 5/3), comenzando desde C, moviendo una celda hacia la izquierda y otra hacia arriba en la tabla, lo que significa descender un quinto (2/3) y ascender un tercio mayor ( 5/4):
Dado que está por debajo de C, debes subir una octava para terminar dentro del rango deseado de proporciones (de 1/1 a 2/1):
Una escala de 12 tonos se obtiene eliminando una nota por cada par de notas enarmónicas. Esto se puede hacer al menos de tres maneras, que tienen en común la eliminación de G ♭ , según una convención válida incluso para escalas pitagóricas basadas en C y escalas de significado de 1/4 de coma. Nótese que es una quinta disminuida , cercana a media octava, por encima del do tónico, que es un intervalo disarmónico; además su relación tiene los valores más grandes en su numerador y denominador de todos los tonos de la escala, lo que la hace menos armoniosa: todas razones para evitarla.
La primera estrategia, que operativamente denotamos aquí como escala simétrica 1 , consiste en seleccionar para eliminar los tonos en las esquinas superior izquierda e inferior derecha de la tabla. La segunda, denominada escala simétrica 2 , consiste en descartar las notas de la primera y última celda de la segunda fila (etiquetadas como " 1 "). La tercera, denominada escala asimétrica , consiste en descartar la primera columna (etiquetada como " 1/9 "). Las escalas de 12 tonos resultantes se muestran a continuación:
En la primera y segunda escala, B ♭ y D son exactamente la inversión entre sí. Esto no es cierto para el tercero. Esta es la razón por la que estas dos escalas se consideran simétricas (aunque la eliminación de G ♭ hace que las 12 escalas tonales, incluidas las producidas con cualquier otro sistema de afinación, sean ligeramente asimétricas).
El sistema asimétrico tiene la ventaja de tener las proporciones "más justas" (las que contienen números más pequeños), nueve quintas puras (factor 3/2), ocho terceras mayores puras (factor 5/4) por diseño, pero también seis terceras menores puras ( factor 6/5). Sin embargo, también contiene dos quintas impuras (por ejemplo, de re a la es 40/27 en lugar de 3/2) y tres terceras menores impuras (por ejemplo, de re a fa es 32/27 en lugar de 6/5), lo que prácticamente limita la modulación. a una gama estrecha de claves. Los acordes de la tónica Do, Sol dominante y Fa subdominante son puros, así como D ♭ , La ♭ , Mi ♭ y los acordes menores Fm, Cm, Gm, Am, Bm y Em, pero no el Dm.
Un inconveniente del sistema asimétrico es que produce 14 intervalos de lobo, en lugar de 12 como para los simétricos.
El si ♭ de la primera escala simétrica se diferencia del si ♭ de las demás escalas por la coma sintónica , siendo superior a 21 céntimos. En escalas igualmente templadas, la diferencia se elimina haciendo que todos los pasos tengan la misma relación de frecuencia.

La construcción de la escala asimétrica se muestra gráficamente en la imagen. Cada bloque tiene la altura en centésimas de las relaciones de frecuencia constructivas 2/1, 3/2 y 5/4. Se pueden reconocer patrones recurrentes. Por ejemplo, muchas veces la siguiente nota se crea reemplazando un bloque de 5/4 y un bloque de 3/2 por un bloque de 2/1, lo que representa una proporción de 16/15.
Para ver una imagen similar, creada utilizando los factores de frecuencia 2, 3 y 5, en lugar de 2/1, 3/2 y 5/4, consulte aquí .
Las proporciones justas utilizadas para construir estas escalas se pueden utilizar como referencia para evaluar la consonancia de intervalos en otras escalas (por ejemplo, consulte esta tabla comparativa ). Sin embargo, la afinación de 5 límites no es el único método para obtener una entonación justa . Es posible construir intervalos justos con proporciones aún más "justas" o, alternativamente, con valores más cercanos a los equivalentes de temperamento igual. Por ejemplo, a veces se utiliza una afinación de 7 límites para obtener un intervalo ligeramente más justo y, en consecuencia, más consonántico para la séptima menor (7/4) y su inversión, la segunda mayor (8/7). A continuación se proporciona una lista de estas razones de referencia, que pueden denominarse intervalos o razones puras o estrictamente justas :
Las celdas resaltadas en amarillo indican intervalos que son más justos que los de las celdas sin color en la misma fila. Los resaltados en cian indican proporciones aún más justas.
Tenga en cuenta que las proporciones 45/32 y 64/45 para los tritonos (cuarta aumentada y quinta disminuida) no se consideran estrictamente justas en todos los contextos, pero son las más justas posibles en las escalas de afinación de 5 límites antes mencionadas. Una escala asimétrica extendida de 5 límites (ver más abajo) proporciona proporciones ligeramente más justas para ambos tritonos (25/18 y 36/25), cuya pureza también es controvertida. La afinación de 7 límites permite las proporciones más justas posibles, es decir, 7/5 (aproximadamente 582,512 centavos, también conocido como tritono séptimo ) y 10/7 (aproximadamente 617,488 centavos). Estas proporciones son más consonantes que 17/12 (unos 603.000 céntimos) y 24/17 (unos 597.000 céntimos), que se pueden obtener con una afinación de 17 límites, aunque estas últimas también son bastante comunes, ya que se acercan más a la igualdad. Valor templado de 600.000 céntimos.
El intervalo de 7/4 mencionado anteriormente (alrededor de 968,826 cents), también conocido como séptima menor séptima o séptima armónica, ha sido un tema polémico a lo largo de la historia de la teoría musical; es 31 centavos más plano que una séptima menor de igual temperamento.
Las tablas anteriores muestran solo las proporciones de frecuencia de cada tono con respecto a la nota base C. Sin embargo, se pueden formar intervalos comenzando desde cada una de las doce notas. Así, se pueden definir doce intervalos para cada tipo de intervalo (doce unísonos, doce semitonos , doce intervalos compuestos por 2 semitonos, doce intervalos compuestos por 3 semitonos, etc.).
En la afinación de 5 límites, cada uno de los tipos de intervalos, excepto los unísonos y las octavas, tiene tres o incluso cuatro tamaños diferentes. Éste es el precio que se paga por buscar una entonación justa. Las tablas de la derecha y de abajo muestran sus relaciones de frecuencia y sus tamaños aproximados en centavos, para la "escala asimétrica". Tablas similares, para la "escala simétrica 1", se publican aquí y aquí. Los nombres de los intervalos se dan en su forma abreviada estándar. Por ejemplo, el tamaño del intervalo de C a G, que es una quinta justa ( P5 ), se puede encontrar en la séptima columna de la fila denominada C. Los intervalos puros, tal como se definen anteriormente, se muestran en negrita (obsérvese que, como se explicó anteriormente, la proporción justamente entonada 45/32 ≈ 590 cents, para A4, no se considera pura).
Un código de colores distingue los intervalos que se desvían de los tamaños de referencia en la tabla de construcción y muestra la magnitud de su desviación. Los intervalos de lobo están marcados en negro. [4]
La razón por la cual los tamaños de los intervalos varían a lo largo de la escala es que los tonos que forman la escala están espaciados de manera desigual. Es decir, las frecuencias definidas por construcción para las doce notas determinan cuatro semitonos diferentes (es decir, intervalos entre notas adyacentes). Por ejemplo:
Por el contrario, en una escala cromática igualmente templada , por definición los doce tonos están igualmente espaciados, teniendo todos los semitonos un tamaño de exactamente
Como consecuencia, todos los intervalos de cualquier tipo dado tienen el mismo tamaño (por ejemplo, todas las terceras mayores tienen el mismo tamaño, todas las quintas tienen el mismo tamaño, etc.). El precio que se paga, en este caso, es que ninguno de ellos está justamente afinado y perfectamente consonante, salvo, claro está, el unísono y la octava.
Tenga en cuenta que el ajuste de 5 límites fue diseñado para maximizar el número de intervalos puros, pero incluso en este sistema varios intervalos son marcadamente impuros (por ejemplo, como se muestra en las figuras, 60 de 144 intervalos se desvían en al menos 19,6 centavos del valor justo). tamaños de referencia entonados mostrados en la tabla de construcción). Además, la afinación de 5 límites produce un número mucho mayor de intervalos de lobo con respecto a la afinación pitagórica , que puede considerarse una afinación de entonación justa de 3 límites. Es decir, mientras que la afinación pitagórica determina sólo 2 intervalos de lobo (una quinta y una cuarta), las escalas simétricas de 5 límites producen 12 de ellos, y la escala asimétrica 14. También es importante señalar que las dos quintas, tres terceras menores, y tres sextas mayores marcadas en naranja en las tablas (proporción 40/27, 32/27 y 27/16 (o G−, E ♭ − y A+ [3] ), aunque no cumplen completamente las condiciones [ 4] para ser intervalos de lobo, se desvían de la proporción pura correspondiente en una cantidad (1 coma sintónica , es decir, 81/80, o alrededor de 21,5 centavos) lo suficientemente grande como para ser percibida claramente como disonante . [5]
Claramente, cuanto más intentamos aumentar el número de intervalos puros y consonánticos , más impuros y disonantes se vuelven los restantes, por compensación. Algunas de las segundas mayores (M2) y séptimas menores (m7) representan la única excepción a esta regla. Como puedes ver en las tablas, los marcados en naranja son puros (10/9 y 16/9), aunque su talla sea 81/80 más estrecha que la talla de referencia correspondiente (9/8 y 9/5).
Para una comparación con otros sistemas de tuning, consulte también esta tabla .
En otros sistemas de afinación, una coma puede definirse como un intervalo de un minuto, igual a la diferencia entre dos tipos de semitonos (diatónico y cromático, también conocido como segunda menor, m2 , o unísono aumentado, A1 ). En este caso, sin embargo, se producen 4 tipos diferentes de semitonos (dos A1, S 1 y S 2 , y dos m2, S 3 y S 4 ), y se pueden definir 12 comas diferentes como las diferencias entre sus tamaños en centésimas, o de manera equivalente como las razones entre sus razones. Entre estos, seleccionamos los seis ascendentes (aquellos con ratio mayor a 1/1, y tamaño positivo en céntimos):
Las otras seis proporciones se descartan porque son justo lo opuesto a éstas y, por lo tanto, tienen exactamente la misma longitud, pero una dirección opuesta (es decir, una dirección descendente, una proporción menor que 1/1 y un tamaño negativo en centavos). . Obtenemos comas de cuatro tamaños diferentes: el diasquisma, la diésis menor, la coma sintónica y la diésis mayor. Dado que S 1 (el justo A1 ) y S 3 (el justo m2 ) son los semitonos que aparecen con más frecuencia en esta escala de 12 tonos (ver tablas arriba), la diesis menor, definida como la relación entre ellos, es la más frecuente. coma observada.
La coma sintónica también se define, en la afinación de 5 límites, como la relación entre el tono mayor (M2 con tamaño 9/8) y el tono menor (M2 con tamaño 10/9). Tenga en cuenta que no se puede definir, en otros sistemas de afinación, como la relación entre semitonos diatónicos y cromáticos (m2/A1), pero es un valor de referencia importante utilizado para afinar la quinta justa en cualquier sistema de afinación en el continuo de temperamento sintónico (incluyendo también significó temperamentos).
Tres de las comas antes mencionadas, a saber, el diasquisma, la diesis y la diesis mayor, cumplen con la definición de segundo disminuido , siendo la diferencia entre los tamaños en centésimas de un semitono diatónico y uno cromático (o equivalentemente la relación entre sus frecuencias proporciones).
Por el contrario, la coma sintónica se define bien como la diferencia en centésimas entre dos semitonos cromáticos (S 2 y S 1 ), o entre dos semitonos diatónicos (S 4 y S 3 ), y no puede considerarse una segunda disminuida.
La tabla anterior utiliza sólo potencias bajas de 3 y 5 para construir las proporciones base. Sin embargo, se puede ampliar fácilmente utilizando potencias positivas y negativas superiores de los mismos números, como 5 2 = 25, 5 −2 = 1/25, 3 3 = 27 o 3 −3 = 1/27. Se puede obtener una escala con 25, 35 o incluso más tonos combinando estas proporciones básicas.
Por ejemplo, se pueden obtener 35 tonos sumando filas en cada dirección de esta manera:
La columna izquierda ( 1/9 ) a veces se elimina (como en la escala asimétrica que se muestra arriba), creando así una tabla asimétrica con un número menor de tonos. Observe que se produce una proporción más justa para la quinta disminuida (CG ♭ = 36/25), con respecto a la afinación restringida de 5 límites descrita anteriormente (donde C a G ♭ - = 64/45). [6]
En la afinación pitagórica, quizás el primer sistema de afinación teorizado en Occidente, [7] los únicos intervalos altamente consonantes eran la quinta justa y su inversión, la cuarta justa . La tercera mayor pitagórica (81:64) y la tercera menor (32:27) eran disonantes , y esto impedía a los músicos utilizar tríadas y acordes , obligándolos durante siglos a escribir música con una textura relativamente simple . A finales de la Edad Media , los músicos se dieron cuenta de que moderando ligeramente el tono de algunas notas, las terceras pitagóricas podían volverse consonantes . Por ejemplo, si disminuye con una coma sintónica (81:80), la frecuencia de E, CE (una tercera mayor) y EG (una tercera menor) se vuelve justa. Es decir, CE se reduce a una proporción justamente entonada de
y al mismo tiempo EG se amplía a la proporción justa de
El inconveniente es que las quintas AE y EB, al aplanar E, se vuelven casi tan disonantes como la quinta del lobo pitagórico . Pero el quinto CG permanece consonante, ya que solo E ha sido aplanado (CE * EG = 5/4 * 6/5 = 3/2), y puede usarse junto con CE para producir una tríada de Do mayor (CEG).
Al generalizar este simple razonamiento, Gioseffo Zarlino , a finales del siglo XVI, creó la primera escala de 7 tonos ( diatónica ) justamente entonada, que contenía quintas perfectas puras (3:2), terceras mayores puras y terceras menores puras:
F → A → C → E → G → B → D
Esta es una secuencia de solo tercios mayores (M3, proporción 5:4) y solo tercios menores (m3, proporción 6:5), comenzando desde F:
F + M3 + m3 + M3 + m3 + M3 + m3
Dado que M3 + m3 = P5 (quinta justa), es decir, 5/4 * 6/5 = 3/2, esto es exactamente equivalente a la escala diatónica obtenida en entonación justa de 5 límites y, por lo tanto, puede verse como un subconjunto de la tabla de construcción utilizada para la escala ( cromática ) de 12 tonos :
donde ambas filas son secuencias de solo quintas, y FA, CE, GB son solo terceras mayores: