Grupo simétrico afín

Estructura matemática

La teselación triangular regular del plano, cuyas simetrías están descritas por el grupo simétrico afín S̃ ₃

Los grupos simétricos afines son una familia de estructuras matemáticas que describen las simetrías de la línea numérica y la teselación triangular regular del plano, así como objetos relacionados de dimensiones superiores. Además de esta descripción geométrica, los grupos simétricos afines pueden definirse de otras maneras: como colecciones de permutaciones (reordenamientos) de los números enteros ( ..., −2, −1, 0, 1, 2, ... ) que son periódicos en un cierto sentido, o en términos puramente algebraicos como un grupo con ciertos generadores y relaciones . Se estudian en combinatoria y teoría de la representación .

Un grupo simétrico finito está formado por todas las permutaciones de un conjunto finito. Cada grupo simétrico afín es una extensión infinita de un grupo simétrico finito. Muchas propiedades combinatorias importantes de los grupos simétricos finitos se pueden extender a los grupos simétricos afines correspondientes. En el caso afín se pueden definir estadísticas de permutación como descensos e inversiones . Al igual que en el caso finito, las definiciones combinatorias naturales de estas estadísticas también tienen una interpretación geométrica.

Los grupos simétricos afines tienen estrechas relaciones con otros objetos matemáticos, incluidos los patrones de malabarismo y ciertos grupos de reflexión complejos . Muchas de sus propiedades combinatorias y geométricas se extienden a la familia más amplia de grupos de Coxeter afines .

Definiciones

El grupo simétrico afín puede definirse de manera equivalente como un grupo abstracto por generadores y relaciones, o en términos de modelos geométricos y combinatorios concretos. ^[1]

Definición algebraica

Diagramas de Dynkin para los grupos simétricos afines en 2 y más de 2 generadores

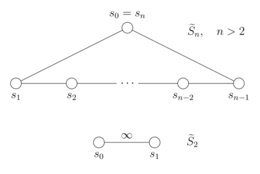
Una forma de definir los grupos es mediante generadores y relaciones . En este tipo de definición, los generadores son un subconjunto de elementos del grupo que, al combinarse, producen todos los demás elementos. Las relaciones de la definición son un sistema de ecuaciones que determinan cuándo dos combinaciones de generadores son iguales. ^{[a] [2]} De esta manera, el grupo simétrico afín se genera mediante un conjunto de n elementos que satisfacen las siguientes relaciones: cuando , ${\displaystyle {\widetilde {S}}_{n}}$ $${\displaystyle s_{0},s_{1},\ldots ,s_{n-1}}$$ ${\displaystyle n\geq 3}$

1. ${\displaystyle s_{i}^{2}=1}$(los generadores son involuciones ),
2. ${\displaystyle s_{i}s_{j}=s_{j}s_{i}}$si j no es uno de , lo que indica que para estos pares de generadores, la operación de grupo es conmutativa , y ${\displaystyle i-1,i,i+1}$
3. ${\displaystyle s_{i}s_{i+1}s_{i}=s_{i+1}s_{i}s_{i+1}}$.

En las relaciones anteriores, los índices se toman módulo n , de modo que la tercera relación incluye como caso particular . (La segunda y tercera relación a veces se denominan relaciones de trenza . ^[3] ) Cuando , el grupo simétrico afín es el grupo diedro infinito generado por dos elementos sujetos únicamente a las relaciones . ^[4] ${\displaystyle s_{0}s_{n-1}s_{0}=s_{n-1}s_{0}s_{n-1}}$ ${\displaystyle n=2}$ ${\displaystyle {\widetilde {S}}_{2}}$ ${\displaystyle s_{0},s_{1}}$ ${\displaystyle s_{0}^{2}=s_{1}^{2}=1}$

Estas relaciones se pueden reescribir en la forma especial que define los grupos de Coxeter , por lo que los grupos simétricos afines son grupos de Coxeter, con los como sus conjuntos generadores de Coxeter. ^[4] Cada grupo de Coxeter puede representarse mediante un diagrama de Coxeter-Dynkin , en el que los vértices corresponden a los generadores y las aristas codifican las relaciones entre ellos. ^[5] Para , el diagrama de Coxeter-Dynkin de es el n -ciclo (donde las aristas corresponden a las relaciones entre pares de generadores consecutivos y la ausencia de una arista entre otros pares de generadores indica que conmutan), mientras que para consta de dos nodos unidos por una arista etiquetada . ^{[6] [4]} ${\displaystyle s_{i}}$ ${\displaystyle n\geq 3}$ ${\displaystyle {\widetilde {S}}_{n}}$ ${\displaystyle n=2}$ ${\displaystyle \infty }$

Definición geométrica

Cuando n = 3 , el espacio V es un plano bidimensional y las reflexiones se producen a través de líneas. Los puntos de la red de raíces Λ están rodeados con un círculo.

En el espacio euclidiano con coordenadas , el conjunto V de puntos para los cuales forma un (hiper)plano , un subespacio ( n − 1) -dimensional. Para cada par de elementos distintos i y j de y cada entero k , el conjunto de puntos en V que satisfacen forma un subespacio ( n − 2) -dimensional dentro de V , y hay una única reflexión de V que fija este subespacio. Entonces el grupo simétrico afín puede realizarse geométricamente como una colección de funciones de V sobre sí mismo, las composiciones de estas reflexiones. ^[7] ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle (x_{1},\ldots ,x_{n})}$ ${\displaystyle x_{1}+x_{2}+\cdots +x_{n}=0}$ ${\displaystyle \{1,\ldots ,n\}}$ ${\displaystyle x_{i}-x_{j}=k}$ ${\displaystyle {\widetilde {S}}_{n}}$

Dentro de V , el subconjunto de puntos con coordenadas enteras forma la red raíz , Λ . Es el conjunto de todos los vectores enteros tales que . ^[8] Cada reflexión preserva esta red, y por lo tanto la red es preservada por todo el grupo. ^[9] ${\displaystyle (a_{1},\ldots ,a_{n})}$ ${\displaystyle a_{1}+\cdots +a_{n}=0}$

Los subespacios fijos de estas reflexiones dividen a V en símplices congruentes , llamados nichos . ^[10] La situación cuando se muestra en la figura; en este caso, la red raíz es una red triangular, las líneas reflectantes dividen a V en nichos de triángulos equiláteros y las raíces son los centros de hexágonos no superpuestos compuestos por seis nichos triangulares. ^{[11] [12]} ${\displaystyle n=3}$

Reflexiones y nichos para el grupo simétrico afín. El nicho fundamental está sombreado.

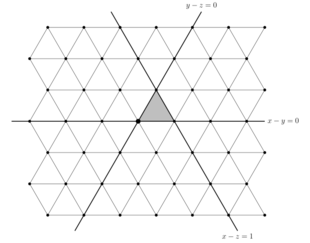
Para traducir entre las definiciones geométricas y algebraicas, se fija una alcoba y se consideran los n hiperplanos que forman su límite. Las reflexiones a través de estos hiperplanos límite pueden identificarse con los generadores de Coxeter. En particular, hay una única alcoba (la alcoba fundamental ) que consiste en puntos tales que , que está limitada por los hiperplanos ..., e ilustrada en el caso . Para , se puede identificar la reflexión a través de con el generador de Coxeter , y también identificar la reflexión a través de con el generador . ^[10] ${\displaystyle (x_{1},\ldots ,x_{n})}$ ${\displaystyle x_{1}\geq x_{2}\geq \cdots \geq x_{n}\geq x_{1}-1}$ ${\displaystyle x_{1}-x_{2}=0,}$ ${\displaystyle x_{2}-x_{3}=0,}$ ${\displaystyle x_{1}-x_{n}=1,}$ ${\displaystyle n=3}$ ${\displaystyle i=1,\ldots ,n-1}$ ${\displaystyle x_{i}-x_{i+1}=0}$ ${\displaystyle s_{i}}$ ${\displaystyle x_{1}-x_{n}=1}$ ${\displaystyle s_{0}=s_{n}}$

Definición combinatoria

Los elementos del grupo simétrico afín pueden realizarse como un grupo de permutaciones periódicas de los números enteros. En particular, digamos que una función es una permutación afín si ${\displaystyle u\colon \mathbb {Z} \to \mathbb {Z} }$

• es una biyección (cada entero aparece como el valor de para exactamente uno ), ${\displaystyle u(x)}$ ${\displaystyle x}$
• ${\displaystyle u(x+n)=u(x)+n}$para todos los enteros x (la función es equivariante al desplazarse por ), y ${\displaystyle n}$
• ${\displaystyle u(1)+u(2)+\cdots +u(n)=1+2+\cdots +n={\frac {n(n+1)}{2}}}$, el ésimo número triangular . ${\displaystyle n}$

Para cada permutación afín, y más generalmente para cada biyección equivalente a un desplazamiento, todos los números deben ser distintos módulo n . Una permutación afín está determinada de manera única por su notación de ventana , porque todos los demás valores de se pueden encontrar desplazando estos valores. Por lo tanto, las permutaciones afines también se pueden identificar con tuplas de números enteros que contienen un elemento de cada clase de congruencia módulo n y suman . ^[13] ${\displaystyle u(1),\ldots ,u(n)}$ ${\displaystyle [u(1),\ldots ,u(n)]}$ ${\displaystyle u}$ ${\displaystyle [u(1),\ldots ,u(n)]}$ ${\displaystyle 1+2+\cdots +n}$

Para traducir entre las definiciones combinatorias y algebraicas, se puede identificar el generador de Coxeter con la permutación afín que tiene notación de ventana , y también identificar el generador con la permutación afín . De manera más general, cada reflexión (es decir, un conjugado de uno de los generadores de Coxeter) se puede describir de manera única de la siguiente manera: para enteros distintos i , j en y un entero arbitrario k , asigna i a j − kn , asigna j a i + kn y fija todas las entradas no congruentes con i o j módulo n . ^[14] ${\displaystyle i=1,\ldots ,n-1}$ ${\displaystyle s_{i}}$ ${\displaystyle [1,2,\ldots ,i-1,i+1,i,i+2,\ldots ,n]}$ ${\displaystyle s_{0}=s_{n}}$ ${\displaystyle [0,2,3,\ldots ,n-2,n-1,n+1]}$ ${\displaystyle \{1,\ldots ,n\}}$

Representación como matrices

Representación matricial de la permutación afín [2, 0, 4], con las convenciones de que los 1 se reemplazan por • y los 0 se omiten. Se muestran los etiquetados de filas y columnas.

Las permutaciones afines se pueden representar como matrices de permutación periódicas infinitas . ^[15] Si es una permutación afín, la matriz correspondiente tiene la entrada 1 en la posición en la cuadrícula infinita para cada entero i , y todas las demás entradas son iguales a 0. Como u es una biyección, la matriz resultante contiene exactamente un 1 en cada fila y columna. La condición de periodicidad en el mapa u asegura que la entrada en la posición sea igual a la entrada en la posición para cada par de enteros . ^[15] Por ejemplo, una parte de la matriz para la permutación afín se muestra en la figura. En la fila 1, hay un 1 en la columna 2; en la fila 2, hay un 1 en la columna 0; y en la fila 3, hay un 1 en la columna 4. El resto de las entradas en esas filas y columnas son todas 0, y todas las demás entradas en la matriz están fijadas por la condición de periodicidad. ${\displaystyle u:\mathbb {Z} \to \mathbb {Z} }$ ${\displaystyle (i,u(i))}$ ${\displaystyle \mathbb {Z} \times \mathbb {Z} }$ ${\displaystyle (a,b)}$ ${\displaystyle (a+n,b+n)}$ ${\displaystyle (a,b)}$ ${\displaystyle [2,0,4]\in {\widetilde {S}}_{3}}$

Relación con el grupo simétrico finito

El grupo simétrico afín contiene el grupo simétrico finito de permutaciones de elementos como subgrupo y como grupo cociente . ^[16] Estas conexiones permiten una traducción directa entre las definiciones combinatorias y geométricas del grupo simétrico afín. ${\displaystyle {\widetilde {S}}_{n}}$ ${\displaystyle S_{n}}$ ${\displaystyle n}$

Como subgrupo

Existe una forma canónica de elegir un subgrupo de que sea isomorfo al grupo simétrico finito . En términos de la definición algebraica, este es el subgrupo de generado por (excluyendo la reflexión simple ). Geométricamente, esto corresponde al subgrupo de transformaciones que fijan el origen, mientras que combinatoriamente corresponde a las notaciones de ventana para las cuales (es decir, en las que la notación de ventana es la notación unifilar de una permutación finita). ^{[17] [18]} ${\displaystyle {\widetilde {S}}_{n}}$ ${\displaystyle S_{n}}$ ${\displaystyle {\widetilde {S}}_{n}}$ ${\displaystyle s_{1},\ldots ,s_{n-1}}$ ${\displaystyle s_{0}=s_{n}}$ ${\displaystyle \{u(1),\ldots ,u(n)\}=\{1,2,\ldots ,n\}}$

Si es la notación de ventana de un elemento de esta copia estándar de , su acción sobre el hiperplano V en se da por la permutación de coordenadas: . ^[19] (En este artículo, la acción geométrica de las permutaciones y permutaciones afines está a la derecha; por lo tanto, si u y v son dos permutaciones afines, la acción de uv sobre un punto se da aplicando primero u y luego v ). ${\displaystyle u=[u(1),u(2),\ldots ,u(n)]}$ ${\displaystyle S_{n}\subset {\widetilde {S}}_{n}}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle (x_{1},x_{2},\ldots ,x_{n})\cdot u=(x_{u(1)},x_{u(2)},\ldots ,x_{u(n)})}$

También hay muchas copias no estándar de contenidas en . Una construcción geométrica consiste en elegir cualquier punto a en Λ (es decir, un vector entero cuyas coordenadas suman 0); el subgrupo de isometrías que fijan a es isomorfo a . ^[20] ${\displaystyle S_{n}}$ ${\displaystyle {\widetilde {S}}_{n}}$ ${\displaystyle ({\widetilde {S}}_{n})_{a}}$ ${\displaystyle {\widetilde {S}}_{n}}$ ${\displaystyle S_{n}}$

Como cociente

Existe una función simple (técnicamente, un homomorfismo de grupo sobreyectivo ) π de sobre el grupo simétrico finito . En términos de la definición combinatoria, una permutación afín se puede mapear a una permutación reduciendo las entradas de la ventana módulo n a elementos de , dejando la notación unifilar de una permutación. ^[21] En este artículo, la imagen de una permutación afín u se denomina permutación subyacente de u . ${\displaystyle {\widetilde {S}}_{n}}$ ${\displaystyle S_{n}}$ ${\displaystyle \{1,2,\ldots ,n\}}$ ${\displaystyle \pi (u)}$

El mapa π envía al generador de Coxeter a la permutación cuya notación unifilar y notación cíclica son y , respectivamente. ^{[22] [21]} ${\displaystyle s_{0}=[0,2,3,4,\ldots ,n-2,n-1,n+1]}$ ${\displaystyle [n,2,3,4,\ldots ,n-2,n-1,1]}$ ${\displaystyle (1\;n)}$

El núcleo de π es por definición el conjunto de permutaciones afines cuya permutación subyacente es la identidad . Las notaciones de ventana de tales permutaciones afines son de la forma , donde es un vector entero tal que , es decir, donde . Geométricamente, este núcleo consiste en las traslaciones , las isometrías que desplazan todo el espacio V sin rotarlo ni reflejarlo. ^[23] En un abuso de la notación , el símbolo Λ se utiliza en este artículo para los tres conjuntos (vectores enteros en V , permutaciones afines con la permutación subyacente la identidad y traslaciones); en los tres entornos, la operación de grupo natural convierte a Λ en un grupo abeliano , generado libremente por los n − 1 vectores . ^[24] ${\displaystyle [1-a_{1}\cdot n,2-a_{2}\cdot n,\ldots ,n-a_{n}\cdot n]}$ ${\displaystyle (a_{1},a_{2},\ldots ,a_{n})}$ ${\displaystyle a_{1}+a_{2}+\ldots +a_{n}=0}$ ${\displaystyle (a_{1},\ldots ,a_{n})\in \Lambda }$ ${\displaystyle \{(1,-1,0,\ldots ,0),(0,1,-1,\ldots ,0),\ldots ,(0,\ldots ,0,1,-1)\}}$

Conexión entre las definiciones geométricas y combinatorias

Alcobas para permutaciones afines etiquetadas. Una alcoba A se etiqueta con la notación de ventana para una permutación u si u envía la alcoba fundamental (sombreada) a A. Los números negativos se indican con barras superpuestas. ${\displaystyle {\widetilde {S}}_{3}}$

El grupo simétrico afín tiene como subgrupo normal a Λ , y es isomorfo al producto semidirecto de este subgrupo con el grupo simétrico finito , donde la acción de sobre Λ es por permutación de coordenadas. En consecuencia, cada elemento u de tiene una realización única como producto donde es una permutación en la copia estándar de en y es una traslación en Λ . ^[25] ${\displaystyle {\widetilde {S}}_{n}}$ $${\displaystyle {\widetilde {S}}_{n}\cong S_{n}\ltimes \Lambda }$$ ${\displaystyle S_{n}}$ ${\displaystyle S_{n}}$ ${\displaystyle {\widetilde {S}}_{n}}$ ${\displaystyle u=r\cdot t}$ ${\displaystyle r}$ ${\displaystyle S_{n}}$ ${\displaystyle {\widetilde {S}}_{n}}$ ${\displaystyle t}$

Este punto de vista permite una traducción directa entre las definiciones combinatorias y geométricas de : si uno escribe donde y entonces la permutación afín u corresponde al movimiento rígido de V definido por ^[25] ${\displaystyle {\widetilde {S}}_{n}}$ ${\displaystyle [u(1),\ldots ,u(n)]=[r_{1}-a_{1}\cdot n,\ldots ,r_{n}-a_{n}\cdot n]}$ ${\displaystyle r=[r_{1},\ldots ,r_{n}]=\pi (u)}$ ${\displaystyle (a_{1},a_{2},\ldots ,a_{n})\in \Lambda }$ $${\displaystyle (x_{1},\ldots ,x_{n})\cdot u=\left(x_{r(1)}+a_{1},\ldots ,x_{r(n)}+a_{n}\right).}$$

Además, como ocurre con todo grupo de Coxeter afín, el grupo simétrico afín actúa transitivamente y libremente sobre el conjunto de nichos: por cada dos nichos, un único elemento del grupo lleva un nicho al otro. ^[26] Por lo tanto, hacer una elección arbitraria de nicho coloca al grupo en correspondencia biunívoca con los nichos: el elemento identidad corresponde a , y todo otro elemento del grupo g corresponde al nicho que es la imagen de bajo la acción de g . ^[27] ${\displaystyle A_{0}}$ ${\displaystyle A_{0}}$ ${\displaystyle A=A_{0}\cdot g}$ ${\displaystyle A_{0}}$

Ejemplo:n = 2

El grupo simétrico afín actúa sobre la línea V en el plano euclidiano. Las reflexiones se producen a través de las líneas discontinuas. Los vectores de la red de raíces Λ están marcados. ${\displaystyle {\widetilde {S}}_{2}}$

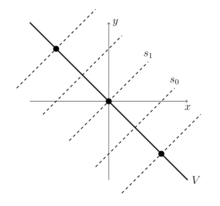
Algebraicamente, es el grupo diedro infinito, generado por dos generadores sujetos a las relaciones . ^[4] Cualquier otro elemento del grupo puede escribirse como un producto alterno de copias de y . ^[28] ${\displaystyle {\widetilde {S}}_{2}}$ ${\displaystyle s_{0},s_{1}}$ ${\displaystyle s_{0}^{2}=s_{1}^{2}=1}$ ${\displaystyle s_{0}}$ ${\displaystyle s_{1}}$

Combinatoriamente, la permutación afín tiene notación de ventana , correspondiente a la biyección para cada entero k . La permutación afín tiene notación de ventana , correspondiente a la biyección para cada entero k . Otros elementos tienen las siguientes notaciones de ventana: ${\displaystyle s_{1}}$ ${\displaystyle [2,1]}$ ${\displaystyle 2k\mapsto 2k-1,2k-1\mapsto 2k}$ ${\displaystyle s_{0}}$ ${\displaystyle [0,3]}$ ${\displaystyle 2k\mapsto 2k+1,2k+1\mapsto 2k}$

${\displaystyle {\begin{aligned}\overbrace {s_{0}s_{1}\cdots s_{0}s_{1}} ^{2k{\text{ factors}}}&=[1+2k,2-2k],\\[5pt]\overbrace {s_{1}s_{0}\cdots s_{1}s_{0}} ^{2k{\text{ factors}}}&=[1-2k,2+2k],\\[5pt]\overbrace {s_{0}s_{1}\cdots s_{0}} ^{2k+1{\text{ factors}}}&=[2+2k,1-2k],\\[5pt]\overbrace {s_{1}s_{0}\cdots s_{1}} ^{2k+1{\text{ factors}}}&=[2-2(k+1),1+2(k+1)].\end{aligned}}}$

Geométricamente, el espacio V sobre el que actúa es una línea, con infinitas reflexiones igualmente espaciadas. ^[29] Es natural identificar la línea V con la línea real , con reflexión alrededor del punto 0 , y con reflexión alrededor del punto 1 . En este caso, la reflexión se refleja a través del punto – k para cualquier entero k , la composición traslada la línea por –2 , y la composición traslada la línea por 2 . ^{[30] [29]} ${\displaystyle {\widetilde {S}}_{2}}$ ${\displaystyle \mathbb {R} ^{1}}$ ${\displaystyle s_{0}}$ ${\displaystyle s_{1}}$ ${\displaystyle (s_{0}s_{1})^{k}s_{0}}$ ${\displaystyle s_{0}s_{1}}$ ${\displaystyle s_{1}s_{0}}$

Estadísticas de permutación y patrones de permutación

Muchas estadísticas de permutación y otras características de la combinatoria de permutaciones finitas pueden extenderse al caso afín. ^[31]

Descensos, longitudes e inversiones

La longitud de un elemento g de un grupo de Coxeter G es el número más pequeño k tal que g puede escribirse como un producto de k generadores de Coxeter de G . ^[32] Geométricamente, la longitud de un elemento g en es el número de hiperplanos reflectores que separan y , donde es la alcoba fundamental (el símplex limitado por los hiperplanos reflectores de los generadores de Coxeter ). ^{[b] [33]} Combinatoriamente, la longitud de una permutación afín se codifica en términos de una noción apropiada de inversiones : para una permutación afín u , la longitud es ^[34] Alternativamente, es el número de clases de equivalencia de pares tales que y bajo la relación de equivalencia si para algún entero k . La función generadora para la longitud en es ^{[35] [36]} ${\displaystyle \ell (g)}$ ${\displaystyle g=s_{i_{1}}\cdots s_{i_{k}}}$ ${\displaystyle {\widetilde {S}}_{n}}$ ${\displaystyle A_{0}}$ ${\displaystyle A_{0}\cdot g}$ ${\displaystyle A_{0}}$ ${\displaystyle s_{0},s_{1},\ldots ,s_{n-1}}$ $${\displaystyle \ell (u)=\#\left\{(i,j)\colon i\in \{1,\ldots ,n\},i<j,{\text{ and }}u(i)>u(j)\right\}.}$$ ${\displaystyle (i,j)\in \mathbb {Z} \times \mathbb {Z} }$ ${\displaystyle i<j}$ ${\displaystyle u(i)>u(j)}$ ${\displaystyle (i,j)\equiv (i',j')}$ ${\displaystyle (i-i',j-j')=(kn,kn)}$ ${\displaystyle {\widetilde {S}}_{n}}$ $${\displaystyle \sum _{g\in {\widetilde {S}}_{n}}q^{\ell (g)}={\frac {1-q^{n}}{(1-q)^{n}}}.}$$

De manera similar, existe un análogo afín de los descensos en permutaciones: una permutación afín u tiene un descenso en la posición i si . (Por periodicidad, u tiene un descenso en la posición i si y solo si tiene un descenso en la posición para todos los enteros k .) Algebraicamente, los descensos corresponden a los descensos por la derecha en el sentido de los grupos de Coxeter; es decir, i es un descenso de u si y solo si . ^[37] Los descensos por la izquierda (es decir, aquellos índices i tales que ) son los descensos de la permutación afín inversa ; equivalentemente, son los valores i tales que i ocurre antes de i − 1 en la secuencia . ^[38] Geométricamente, i es un descenso de u si y solo si el hiperplano fijo de separa las alcobas y ^[39] ${\displaystyle u(i)>u(i+1)}$ ${\displaystyle i+kn}$ ${\displaystyle \ell (u\cdot s_{i})<\ell (u)}$ ${\displaystyle \ell (s_{i}\cdot u)<\ell (u)}$ ${\displaystyle u^{-1}}$ ${\displaystyle \ldots ,u(-2),u(-1),u(0),u(1),u(2),\ldots }$ ${\displaystyle s_{i}}$ ${\displaystyle A_{0}}$ ${\displaystyle A_{0}\cdot u.}$

Como sólo hay un número finito de posibilidades para el número de descensos de una permutación afín, pero infinitas permutaciones afines, no es posible formar ingenuamente una función generadora para permutaciones afines por número de descensos (un análogo afín de los polinomios eulerianos ). ^[40] Una posible resolución es considerar los descensos afines (equivalentemente, descensos cíclicos) en el grupo simétrico finito . ^[11] Otra es considerar simultáneamente la longitud y el número de descensos de una permutación afín. La función generadora multivariante para estas estadísticas simultáneamente para todo n es donde des( w ) es el número de descensos de la permutación afín w y es la función q -exponencial . ^[41] ${\displaystyle S_{n}}$ ${\displaystyle {\widetilde {S}}_{n}}$ $${\displaystyle \sum _{n\geq 1}{\frac {x^{n}}{1-q^{n}}}\sum _{w\in {\widetilde {S}}_{n}}t^{\operatorname {des} (w)}q^{\ell (w)}=\left[{\frac {x\cdot {\frac {\partial }{\partial {x}}}\log(\exp(x;q))}{1-t\exp(x;q)}}\right]_{x\mapsto x{\frac {1-t}{1-q}}}}$$ ${\displaystyle \exp(x;q)=\sum _{n\geq 0}{\frac {x^{n}(1-q)^{n}}{(1-q)(1-q^{2})\cdots (1-q^{n})}}}$

Tipo de ciclo y duración de la reflexión

Cualquier biyección divide los números enteros en una lista (posiblemente infinita) de ciclos (posiblemente infinitos): para cada número entero i , el ciclo que contiene a i es la secuencia donde la exponenciación representa la composición funcional. Para una permutación afín u , las siguientes condiciones son equivalentes: todos los ciclos de u son finitos, u tiene orden finito y la acción geométrica de u sobre el espacio V tiene al menos un punto fijo. ^[42] ${\displaystyle u:\mathbb {Z} \to \mathbb {Z} }$ ${\displaystyle (\ldots ,u^{-2}(i),u^{-1}(i),i,u(i),u^{2}(i),\ldots )}$

La longitud de reflexión de un elemento u de es el número k más pequeño tal que existen reflexiones tales que . (En el grupo simétrico, las reflexiones son transposiciones, y la longitud de reflexión de una permutación u es , donde es el número de ciclos de u . ^[16] ) En (Lewis et al. 2019), se demostró la siguiente fórmula para la longitud de reflexión de una permutación afín u : para cada ciclo de u , defina el peso como el entero k tal que las entradas consecutivas congruentes módulo n difieren exactamente en kn . Forme una tupla de pesos de ciclo de u (contando las traslaciones del mismo ciclo por múltiplos de n solo una vez), y defina la nulidad como el tamaño de la partición de conjunto más pequeña de esta tupla de modo que cada parte sume 0. Entonces la longitud de reflexión de u es donde es la permutación subyacente de u . ^[43] ${\displaystyle \ell _{R}(u)}$ ${\displaystyle {\widetilde {S}}_{n}}$ ${\displaystyle r_{1},\ldots ,r_{k}}$ ${\displaystyle u=r_{1}\cdots r_{k}}$ ${\displaystyle n-c(u)}$ ${\displaystyle c(u)}$ ${\displaystyle \nu (u)}$ $${\displaystyle \ell _{R}(u)=n-2\nu (u)+c(\pi (u)),}$$ ${\displaystyle \pi (u)}$

Para cada permutación afín u , existe una elección de subgrupo W de tal que , , y para la forma estándar implicada por este producto semidirecto, las longitudes de reflexión son aditivas, es decir, . ^[20] ${\displaystyle {\widetilde {S}}_{n}}$ ${\displaystyle W\cong S_{n}}$ ${\displaystyle {\widetilde {S}}_{n}=W\ltimes \Lambda }$ ${\displaystyle u=w\cdot t}$ ${\displaystyle \ell _{R}(u)=\ell _{R}(w)+\ell _{R}(t)}$

Elementos totalmente conmutativos y evitación de patrones

Una palabra reducida para un elemento g de un grupo de Coxeter es una tupla de generadores de Coxeter de longitud mínima posible tal que . ^[32] El elemento g se llama completamente conmutativo si cualquier palabra reducida puede transformarse en cualquier otra intercambiando secuencialmente pares de factores que conmutan. ^[44] Por ejemplo, en el grupo simétrico finito , el elemento es completamente conmutativo, ya que sus dos palabras reducidas y pueden conectarse intercambiando factores conmutativos, pero no es completamente conmutativo porque no hay forma de llegar a la palabra reducida a partir de la palabra reducida por conmutaciones. ^[45] ${\displaystyle (s_{i_{1}},\ldots ,s_{i_{\ell (g)}})}$ ${\displaystyle g=s_{i_{1}}\cdots s_{i_{\ell (g)}}}$ ${\displaystyle S_{4}}$ ${\displaystyle 2143=(12)(34)}$ ${\displaystyle (s_{1},s_{3})}$ ${\displaystyle (s_{3},s_{1})}$ ${\displaystyle 4132=(142)(3)}$ ${\displaystyle (s_{3},s_{2},s_{3},s_{1})}$ ${\displaystyle (s_{2},s_{3},s_{2},s_{1})}$

Billey, Jockusch y Stanley (1993) demostraron que en el grupo simétrico finito , una permutación es completamente conmutativa si y solo si evita el patrón de permutación 321, es decir, si y solo si su notación unifilar no contiene ninguna subsucesión decreciente de tres términos. En (Green 2002), este resultado se extendió a permutaciones afines: una permutación afín u es completamente conmutativa si y solo si no existen números enteros tales que . ^[c] ${\displaystyle S_{n}}$ ${\displaystyle i<j<k}$ ${\displaystyle u(i)>u(j)>u(k)}$

El número de permutaciones afines que evitan un único patrón p es finito si y solo si p evita el patrón 321, ^[47] por lo que, en particular, hay infinitas permutaciones afines totalmente conmutativas. Estas se enumeraron por longitud en (Hanusa y Jones 2010).

Subgrupos parabólicos y otras estructuras

Los subgrupos parabólicos de y sus representantes de coset ofrecen una rica estructura combinatoria. Otros aspectos de los grupos simétricos afines, como su orden de Bruhat y la teoría de representación , también pueden entenderse a través de modelos combinatorios. ^[31] ${\displaystyle {\widetilde {S}}_{n}}$

Subgrupos parabólicos, representantes de clases laterales

Diagrama de ábaco de la permutación afín [−5, 0, 6, 9]

Un subgrupo parabólico estándar de un grupo de Coxeter es un subgrupo generado por un subconjunto de su conjunto generador de Coxeter. ^[48] Los subgrupos parabólicos maximales son aquellos que surgen de omitir un único generador de Coxeter. En , todos los subgrupos parabólicos maximales son isomorfos al grupo simétrico finito . El subgrupo generado por el subconjunto consiste en aquellas permutaciones afines que estabilizan el intervalo , es decir, que mapean cada elemento de este intervalo a otro elemento del intervalo. ^[37] ${\displaystyle {\widetilde {S}}_{n}}$ ${\displaystyle S_{n}}$ ${\displaystyle \{s_{0},\ldots ,s_{n-1}\}\smallsetminus \{s_{i}\}}$ ${\displaystyle [i+1,i+n]}$

Para un elemento fijo i de , sea el subconjunto propio máximo de generadores de Coxeter omitiendo , y sea el subgrupo parabólico generado por J . Cada clase lateral tiene un elemento único de longitud mínima. La colección de tales representantes, denotada , consta de las siguientes permutaciones afines: ^[37] ${\displaystyle \{0,\ldots ,n-1\}}$ ${\displaystyle J=\{s_{0},\ldots ,s_{n-1}\}\smallsetminus \{s_{i}\}}$ ${\displaystyle s_{i}}$ ${\displaystyle ({\widetilde {S}}_{n})_{J}}$ ${\displaystyle g\cdot ({\widetilde {S}}_{n})_{J}}$ ${\displaystyle ({\widetilde {S}}_{n})^{J}}$ $${\displaystyle ({\widetilde {S}}_{n})^{J}=\left\{u\in {\widetilde {S}}_{n}\colon u(i-n+1)<u(i-n+2)<\cdots <u(i-1)<u(i)\right\}.}$$

En el caso particular de que , de modo que sea la copia estándar de dentro de , los elementos de pueden representarse naturalmente mediante diagramas de ábaco : los números enteros se disponen en una franja infinita de ancho n , que aumenta secuencialmente a lo largo de las filas y luego de arriba hacia abajo; los números enteros se encierran en un círculo si se encuentran directamente encima de una de las entradas de la ventana del representante de clase lateral mínima. Por ejemplo, el representante de clase lateral mínima se representa mediante el diagrama de ábaco de la derecha. Para calcular la longitud del representante a partir del diagrama de ábaco, se suma el número de números sin círculo que son más pequeños que la última entrada circulada en cada columna. (En el ejemplo que se muestra, esto da .) ^[49] ${\displaystyle J=\{s_{1},\ldots ,s_{n-1}\}}$ ${\displaystyle ({\widetilde {S}}_{n})_{J}\cong S_{n}}$ ${\displaystyle S_{n}}$ ${\displaystyle {\widetilde {S}}_{n}}$ ${\displaystyle ({\widetilde {S}}_{n})^{J}\cong {\widetilde {S}}_{n}/S_{n}}$ ${\displaystyle u=[-5,0,6,9]}$ ${\displaystyle 5+3+0+1=9}$

Se pueden dar otros modelos combinatorios de representantes de clases laterales de longitud mínima para en términos de particiones de núcleo ( particiones enteras en las que ninguna longitud de gancho es divisible por n ) o particiones acotadas (particiones enteras en las que ninguna parte es mayor que n − 1 ). Bajo estas correspondencias, se puede demostrar que el orden débil de Bruhat en es isomorfo a un cierto subconjunto de la red de Young . ^{[50] [51]} ${\displaystyle {\widetilde {S}}_{n}/S_{n}}$ ${\displaystyle {\widetilde {S}}_{n}/S_{n}}$

Orden de Bruhat

El orden de Bruhat en tiene la siguiente realización combinatoria. Si u es una permutación afín e i y j son números enteros, definamos como el número de números enteros a tales que y . (Por ejemplo, con , se tiene : los tres valores relevantes son , que son mapeados respectivamente por u a 1, 2 y 4.) Entonces para dos permutaciones afines u , v , se tiene que en orden de Bruhat si y solo si para todos los números enteros i , j . ^[52] ${\displaystyle {\widetilde {S}}_{n}}$ ${\displaystyle u[i,j]}$ ${\displaystyle a\leq i}$ ${\displaystyle u(a)\geq j}$ ${\displaystyle u=[2,0,4]\in {\widetilde {S}}_{3}}$ ${\displaystyle u[3,1]=3}$ ${\displaystyle a=0,1,3}$ ${\displaystyle u\leq v}$ ${\displaystyle u[i,j]\leq v[i,j]}$

Teoría de la representación y correspondencia afín Robinson-Schensted

En el grupo simétrico finito, la correspondencia de Robinson–Schensted da una biyección entre el grupo y pares de tablas de Young estándar de la misma forma. Esta biyección juega un papel central en la combinatoria y la teoría de la representación del grupo simétrico . Por ejemplo, en el lenguaje de la teoría de Kazhdan–Lusztig , dos permutaciones se encuentran en la misma celda izquierda si y solo si sus imágenes bajo Robinson–Schensted tienen la misma tabla Q , y en la misma celda derecha si y solo si sus imágenes tienen la misma tabla P. En (Shi 1986), Jian-Yi Shi mostró que las celdas izquierdas para están indexadas en cambio por tabloides , ^[d] y en (Shi 1991) dio un algoritmo para calcular el tabloide análogo a la tabla P para una permutación afín. En (Chmutov, Pylyavskyy y Yudovina 2018), los autores ampliaron el trabajo de Shi para proporcionar una función biyectiva entre y triples que consiste en dos tabloides de la misma forma y un vector entero cuyas entradas satisfacen ciertas desigualdades. Su procedimiento utiliza la representación matricial de permutaciones afines y generaliza la construcción de sombras , introducida en (Viennot 1977). ${\displaystyle (P,Q)}$ ${\displaystyle {\widetilde {S}}_{n}}$ ${\displaystyle {\widetilde {S}}_{n}}$ ${\displaystyle (P,Q,\rho )}$

Realizaciones inversas

Alcobas para etiquetado por permutaciones afines, inversas al etiquetado anterior ${\displaystyle {\widetilde {S}}_{3}}$

En algunas situaciones, se puede desear considerar la acción del grupo simétrico afín sobre o sobre nichos que es inversa a la dada anteriormente. ^[e] Estas realizaciones alternativas se describen a continuación. ${\displaystyle \mathbb {Z} }$

En la acción combinatoria de on , el generador actúa intercambiando los valores i e i + 1 . En la acción inversa, en cambio, intercambia las entradas en las posiciones i e i + 1 . De manera similar, la acción de una reflexión general será intercambiar las entradas en las posiciones j − kn e i + kn para cada k , fijando todas las entradas en posiciones no congruentes con i o j módulo n . ^{[55] [f]} ${\displaystyle {\widetilde {S}}_{n}}$ ${\displaystyle \mathbb {Z} }$ ${\displaystyle s_{i}}$

En la acción geométrica de , el generador actúa sobre una alcoba A reflejándola a través de uno de los planos delimitadores de la alcoba fundamental A ₀ . En la acción inversa, en cambio, refleja A a través de uno de sus propios planos delimitadores. Desde esta perspectiva, una palabra reducida corresponde a un paseo por la alcoba en el espacio teselado V . ^[57] ${\displaystyle {\widetilde {S}}_{n}}$ ${\displaystyle s_{i}}$

Relación con otros objetos matemáticos

Los grupos simétricos afines están estrechamente relacionados con una variedad de otros objetos matemáticos.

Patrones de malabarismo

El patrón de malabarismo 441 se visualiza como un diagrama de arco: la altura de cada lanzamiento corresponde a la longitud de un arco; los dos colores de los nodos son las manos izquierda y derecha del malabarista. Este patrón tiene cuatro cruces, que se repiten periódicamente.

El patrón de malabarismo 441

En (Ehrenborg & Readdy 1996), se da una correspondencia entre permutaciones afines y patrones de malabarismo codificados en una versión de la notación de intercambio de sitios . ^[58] Aquí, un patrón de malabarismo de período n es una secuencia de números enteros no negativos (con ciertas restricciones) que captura el comportamiento de las pelotas lanzadas por un malabarista, donde el número indica el tiempo que el i -ésimo lanzamiento pasa en el aire (equivalentemente, la altura del lanzamiento). ^[g] El número b de pelotas en el patrón es el promedio . ^[60] La correspondencia de Ehrenborg-Readdy asocia a cada patrón de malabarismo de período n la función definida por donde los índices de la secuencia a se toman módulo n . Entonces es una permutación afín en , y además cada permutación afín surge de un patrón de malabarismo de esta manera. ^[58] Bajo esta biyección, la longitud de la permutación afín está codificada por una estadística natural en el patrón de malabarismo: donde es el número de cruces (hasta la periodicidad) en el diagrama de arco de un . Esto permite una prueba elemental de la función generadora para permutaciones afines por longitud. ^[61] ${\displaystyle (a_{1},\ldots ,a_{n})}$ ${\displaystyle a_{i}}$ ${\displaystyle b={\frac {a_{1}+\cdots +a_{n}}{n}}}$ ${\displaystyle {\bf {a}}=(a_{1},\ldots ,a_{n})}$ ${\displaystyle w_{\bf {a}}\colon \mathbb {Z} \to \mathbb {Z} }$ $${\displaystyle w_{\bf {a}}(i)=i+a_{i}-b,}$$ ${\displaystyle w_{\bf {a}}}$ ${\displaystyle {\widetilde {S}}_{n}}$ $${\displaystyle \ell (w_{\bf {a}})=(b-1)n-\operatorname {cross} ({\bf {a}}),}$$ ${\displaystyle \operatorname {cross} ({\bf {a}})}$

Por ejemplo, el patrón de malabarismo 441 tiene y . Por lo tanto, corresponde a la permutación afín . El patrón de malabarismo tiene cuatro cruces y la permutación afín tiene una longitud . ^[62] ${\displaystyle n=3}$ ${\displaystyle b={\frac {4+4+1}{3}}=3}$ ${\displaystyle w_{441}=[1+4-3,2+4-3,3+1-3]=[2,3,1]}$ ${\displaystyle \ell (w_{441})=(3-1)\cdot 3-4=2}$

Se pueden utilizar técnicas similares para derivar la función generadora para representantes de clases laterales mínimas por longitud. ^[63] ${\displaystyle {\widetilde {S}}_{n}/S_{n}}$

Grupos de reflexión complejos

En un espacio de producto interior real de dimensión finita , una reflexión es una transformación lineal que fija un hiperplano lineal puntualmente y niega el vector ortogonal al plano. Esta noción puede extenderse a espacios vectoriales sobre otros cuerpos . En particular, en un espacio de producto interior complejo, una reflexión es una transformación unitaria T de orden finito que fija un hiperplano. ^[h] Esto implica que los vectores ortogonales al hiperplano son vectores propios de T , y el valor propio asociado es una raíz compleja de la unidad . Un grupo de reflexión complejo es un grupo finito de transformaciones lineales sobre un espacio vectorial complejo generado por reflexiones. ^[65]

Los grupos de reflexión complejos fueron clasificados completamente por Shephard y Todd (1954): cada grupo de reflexión complejo es isomorfo a un producto de grupos de reflexión complejos irreducibles, y cada irreducible pertenece a una familia infinita (donde m , p y n son números enteros positivos tales que p divide a m ) o es uno de otros 34 ejemplos (llamados "excepcionales"). El grupo es el grupo simétrico generalizado : algebraicamente, es el producto en corona del grupo cíclico con el grupo simétrico . Concretamente, los elementos del grupo pueden representarse mediante matrices monomiales (matrices que tienen una entrada distinta de cero en cada fila y columna) cuyas entradas distintas de cero son todas raíces m de la unidad. Los grupos son subgrupos de , y en particular el grupo consiste en aquellas matrices en las que el producto de las entradas distintas de cero es igual a 1. ^[66] ${\displaystyle G(m,p,n)}$ ${\displaystyle G(m,1,n)}$ ${\displaystyle (\mathbb {Z} /m\mathbb {Z} )\wr S_{n}}$ ${\displaystyle \mathbb {Z} /m\mathbb {Z} }$ ${\displaystyle S_{n}}$ ${\displaystyle G(m,p,n)}$ ${\displaystyle G(m,1,n)}$ ${\displaystyle G(m,m,n)}$

En (Shi 2002), Shi demostró que el grupo simétrico afín es una cubierta genérica de la familia , en el siguiente sentido: para cada entero positivo m , existe una sobreyección de a , y estas funciones son compatibles con las sobreyecciones naturales cuando éstas provienen de elevar cada entrada a la m / p ésima potencia. Además, estas proyecciones respetan la estructura del grupo de reflexión, en el sentido de que la imagen de cada reflexión en bajo es una reflexión en ; y de manera similar cuando la imagen del elemento estándar de Coxeter en es un elemento de Coxeter en . ^[67] ${\displaystyle \left\{G(m,m,n)\colon m\geq 1\right\}}$ ${\displaystyle \pi _{m}}$ ${\displaystyle {\widetilde {S}}_{n}}$ ${\displaystyle G(m,m,n)}$ ${\displaystyle G(m,m,n)\twoheadrightarrow G(p,p,n)}$ ${\displaystyle p\mid m}$ ${\displaystyle {\widetilde {S}}_{n}}$ ${\displaystyle \pi _{m}}$ ${\displaystyle G(m,m,n)}$ ${\displaystyle m>1}$ ${\displaystyle s_{0}\cdot s_{1}\cdots s_{n-1}}$ ${\displaystyle {\widetilde {S}}_{n}}$ ${\displaystyle G(m,m,n)}$

Álgebras de Lie afines

Cada grupo de Coxeter afín está asociado a un álgebra de Lie afín , un cierto álgebra no asociativa de dimensión infinita con propiedades de teoría de la representación inusualmente agradables. ^[i] En esta asociación, el grupo de Coxeter surge como un grupo de simetrías del espacio raíz del álgebra de Lie (el dual del subálgebra de Cartan ). ^[69] En la clasificación de las álgebras de Lie afines, el asociado a es de tipo (no retorcido) , con matriz de Cartan para y (una matriz circulante ) para . ^[70] ${\displaystyle {\widetilde {S}}_{n}}$ ${\displaystyle A_{n-1}^{(1)}}$ ${\displaystyle \left[{\begin{array}{rr}2&-2\\-2&2\end{array}}\right]}$ ${\displaystyle n=2}$ $${\displaystyle \left[{\begin{array}{rrrrrr}2&-1&0&\cdots &0&-1\\-1&2&-1&\cdots &0&0\\0&-1&2&\cdots &0&0\\\vdots &\vdots &\vdots &\ddots &\vdots &\vdots \\0&0&0&\cdots &2&-1\\-1&0&0&\cdots &-1&2\end{array}}\right]}$$ ${\displaystyle n>2}$

Al igual que otras álgebras de Kac-Moody , las álgebras de Lie afines satisfacen la fórmula de caracteres de Weyl-Kac , que expresa los caracteres del álgebra en términos de sus pesos más altos . ^[71] En el caso de las álgebras de Lie afines, las identidades resultantes son equivalentes a las identidades de Macdonald . En particular, para el álgebra de Lie afín de tipo , asociada al grupo simétrico afín , la identidad de Macdonald correspondiente es equivalente al producto triple de Jacobi . ^[72] ${\displaystyle A_{1}^{(1)}}$ ${\displaystyle {\widetilde {S}}_{2}}$

Grupo trenzado y propiedades de la teoría de grupos

Los grupos de Coxeter tienen una serie de propiedades especiales que no comparten todos los grupos. Entre ellas, se encuentran que su problema verbal es decidible (es decir, existe un algoritmo que puede determinar si cualquier producto dado de los generadores es o no igual al elemento identidad) y que son grupos lineales (es decir, se pueden representar mediante un grupo de matrices invertibles sobre un cuerpo). ^{[73] [74]}

Cada grupo de Coxeter W está asociado a un grupo de Artin–Tits , que se define mediante una presentación similar que omite relaciones de la forma para cada generador s . ^[75] En particular, el grupo de Artin–Tits asociado a se genera mediante n elementos sujetos a las relaciones para (y ninguna otra), donde, como antes, los índices se toman módulo n (por lo que ). ^[76] Se conjetura que los grupos de Artin–Tits de los grupos de Coxeter tienen muchas propiedades interesantes: por ejemplo, se conjetura que están libres de torsión , que tienen un centro trivial , que tienen un problema verbal solucionable y que satisfacen la conjetura. No se sabe que estas conjeturas se cumplan para todos los grupos de Artin–Tits, pero en (Charney & Peifer 2003) se demostró que tiene estas propiedades. (Posteriormente, se han demostrado para los grupos Artin-Tits asociados a grupos Coxeter afines.) ^{[77] [78] [79]} En el caso del grupo simétrico afín, estas pruebas hacen uso de una estructura Garside asociada en el grupo Artin-Tits. ^[80] ${\displaystyle B_{W}}$ ${\displaystyle s^{2}=1}$ ${\displaystyle {\widetilde {S}}_{n}}$ ${\displaystyle \sigma _{0},\sigma _{1},\ldots ,\sigma _{n-1}}$ ${\displaystyle \sigma _{i}\sigma _{i+1}\sigma _{i}=\sigma _{i+1}\sigma _{i}\sigma _{i+1}}$ ${\displaystyle i=0,\ldots ,n-1}$ ${\displaystyle \sigma _{n}=\sigma _{0}}$ ${\displaystyle K(\pi ,1)}$ ${\displaystyle B_{{\widetilde {S}}_{n}}}$

Generadores del grupo Artin-Tits asociados al grupo simétrico afín, representados como trenzas con una hebra fija (para n = 4 ) y como trenzas dibujadas sobre un cilindro (para n = 3 )

Los grupos Artin-Tits a veces también se conocen como grupos trenzados generalizados , porque el grupo Artin-Tits del grupo simétrico (finito) es el grupo trenzado en n hebras. ^[81] No todos los grupos Artin-Tits tienen una representación natural en términos de trenzas geométricas. Sin embargo, el grupo Artin-Tits del grupo hiperoctaédrico (geométricamente, el grupo de simetría del hipercubo n -dimensional ; combinatoriamente, el grupo de permutaciones con signo de tamaño n ) sí tiene dicha representación: está dada por el subgrupo del grupo trenzado en hebras que consiste en aquellas trenzas para las cuales una hebra particular termina en la misma posición en la que comenzó, o equivalentemente como el grupo trenzado de n hebras en una región anular . ^{[76] [82]} Además, el grupo Artin-Tits del grupo hiperoctaédrico se puede escribir como un producto semidirecto de con un grupo cíclico infinito. ^[83] De ello se deduce que puede interpretarse como un cierto subgrupo constituido por trenzas geométricas, y también que es un grupo lineal . ^{[84] [76] [85]} ${\displaystyle B_{S_{n}}}$ ${\displaystyle S_{n}^{\pm }}$ ${\displaystyle n+1}$ ${\displaystyle S_{n}^{\pm }}$ ${\displaystyle B_{{\widetilde {S}}_{n}}}$ ${\displaystyle B_{{\widetilde {S}}_{n}}}$

Grupo simétrico afín extendido

El grupo simétrico afín es un subgrupo del grupo simétrico afín extendido . El grupo extendido es isomorfo al producto corona . Sus elementos son permutaciones afines extendidas : biyecciones tales que para todos los enteros x . A diferencia del grupo simétrico afín, el grupo simétrico afín extendido no es un grupo de Coxeter. Pero tiene un conjunto generador natural que extiende el conjunto generador de Coxeter para : el operador de desplazamiento cuya notación de ventana es genera el grupo extendido con las reflexiones simples, sujeto a las relaciones adicionales . ^[15] ${\displaystyle \mathbb {Z} \wr S_{n}}$ ${\displaystyle u\colon \mathbb {Z} \to \mathbb {Z} }$ ${\displaystyle u(x+n)=u(x)+n}$ ${\displaystyle {\widetilde {S}}_{n}}$ ${\displaystyle \tau }$ ${\displaystyle \tau =[2,3,\ldots ,n,n+1]}$ ${\displaystyle \tau s_{i}\tau ^{-1}=s_{i+1}}$

Combinatoria de otros grupos de Coxeter afines

La acción geométrica del grupo simétrico afín lo ubica naturalmente en la familia de grupos de Coxeter afines , cada uno de los cuales tiene una acción geométrica similar sobre un espacio afín. La descripción combinatoria del también puede extenderse a muchos de estos grupos: en Eriksson & Eriksson (1998), se da una descripción axiomática de ciertos grupos de permutación que actúan sobre (los "grupos de George", en honor a George Lusztig ), y se muestra que son exactamente los grupos de Coxeter "clásicos" de tipos finitos y afines A, B, C y D. (En la clasificación de los grupos de Coxeter afines, el grupo simétrico afín es el tipo A). Por lo tanto, las interpretaciones combinatorias de descensos, inversiones, etc., se trasladan en estos casos. ^[86] Los modelos de ábaco de representantes de clases laterales de longitud mínima para cocientes parabólicos también se han extendido a este contexto. ^[87] ${\displaystyle {\widetilde {S}}_{n}}$ ${\displaystyle {\widetilde {S}}_{n}}$ ${\displaystyle \mathbb {Z} }$

Historia

El estudio de los grupos de Coxeter en general podría decirse que surgió por primera vez en la clasificación de poliedros regulares (los sólidos platónicos ) en la antigua Grecia. El estudio sistemático moderno (que conecta las definiciones algebraicas y geométricas de los grupos de Coxeter finitos y afines) comenzó en el trabajo de Coxeter en la década de 1930. ^[88] La descripción combinatoria del grupo simétrico afín aparece por primera vez en el trabajo de Lusztig (1983), y fue ampliada por Shi (1986); ambos autores utilizaron la descripción combinatoria para estudiar las células de Kazhdan-Lusztig de . ^{[89] [90]} La prueba de que la definición combinatoria concuerda con la definición algebraica fue dada por Eriksson y Eriksson (1998). ^[90] ${\displaystyle {\widetilde {S}}_{n}}$

Referencias

Este artículo fue adaptado de la siguiente fuente bajo licencia CC BY 4.0 (2021) (informes de los revisores): Joel B. Lewis (21 de abril de 2021), "Affine symmetry group" (PDF) , WikiJournal of Science , 4 (1): 3, doi : 10.15347/WJS/2021.003 , ISSN  2470-6345, Wikidata  Q100400684

1. Shi (1986), pág. 66.
2. Gallian (2013), Capítulo 26.
3. Stembridge (1996), pág. 355.
4. Björner y Brenti (2005), págs.
5. Humphreys (1990), pág. 31.
6. Björner y Brenti (2005), pág. 2.
7. Humphreys (1990), págs. 87–89, 95–6.
8. Humphreys (1990), pág. 41.
9. Humphreys (1990), pág. 87.
10. Humphreys (1990), Sección 4.3.
11. Petersen (2015), Capítulo 14.
12. Coxeter (1973), Capítulo 5.
13. Björner y Brenti (2005), Capítulo 8.3.
14. Björner y Brenti (2005), Proposición 8.3.5.
15. Chmutov, Pylyavskyy y Yudovina (2018), Sección 1.6.
16. Lewis y otros (2019).
17. Björner y Brenti (2005), pág. 260.
18. Kane (2001), Sección 11-3.
19. Lewis y col. (2019), pág. 4118.
20. Lewis et al. (2019), Corolario 2.5.
21. Shi (1986), págs. 85-6.
22. Petersen (2015), Sección 14.4.1.
23. Kane (2001), Sección 11-1.
24. Humphreys (1990), Sección 2.10.
25. Lewis et al. (2019), Sección 4.1.
26. Humphreys (1990), Capítulo 4.5.
27. Humphreys (1990), Capítulo 4.
28. Gallian (2013), pág. 454.
29. Gallian (2013), pág. 455.
30. Lewis y Reiner (2016), Sección 4.1.
31. Björner y Brenti (2005), pág. 245.
32. Björner y Brenti (2005), pág. 15.
33. Humphreys (1990), pág. 93.
34. Björner y Brenti (2005), pág. 261.
35. Björner y Brenti (2005), pág. 208.
36. Björner y Brenti (1996), Cor. 4.7.
37. Björner y Brenti (2005), pág. 263.
38. Chmutov, Lewis y Pylyavskyy (2022), Sección 3.2.
39. Shi (1987), pág. 55.
40. Reiner (1995), pág. 2.
41. Reiner (1995), Teorema 6.
42. Lewis et al. (2019), Proposiciones 1.31 y 4.24.
43. Lewis y col. (2019), Teorema 4.25.
44. Stembridge (1996), pág. 353.
45. Billey, Jockusch y Stanley (1993), pág. 358.
46. Hanusa y Jones (2010), pág. 1345.
47. Crites (2010), Teorema 1.
48. Björner y Brenti (2005), pág. 38.
49. Hanusa y Jones (2010), Sección 2.2.
50. Lapointe y Morse (2005).
51. Berg, Jones y Vazirani (2009).
52. Björner y Brenti (2005), pág. 264.
53. Chmutov y col. (2022), Sección 2.2.2.
54. Shi (1986), pág. 68.
55. Knutson, Lam y Speyer (2013), Sección 2.1.
56. Como en (Cameron 1994, Sección 3.5).
57. Como en, por ejemplo, (Beazley et al. 2015), (Lam 2015).
58. Polster (2003), pág. 42.
59. Polster (2003), pág. 22.
60. Polster (2003), pág. 15.
61. Polster (2003), pág. 43.
62. Polster (2003), sección 2.7.
63. Clark y Ehrenborg (2011), Teorema 2.2.
64. Lehrer y Taylor (2009), pág. 9.
65. Lehrer y Taylor (2009), pág. 10.
66. Lehrer y Taylor (2009), Capítulo 2.
67. Lewis (2020), Sección 3.2.
68. Kac (1990), Introducción.
69. Kac (1990), Capítulo 3.
70. Kac (1990), Capítulo 4.
71. Kac (1990), Capítulo 10.
72. Kac (1990), Capítulo 12.
73. Björner y Brenti (2005), págs.75, 92.
74. McCammond (2017), pág. 6.
75. McCammond (2017), Sección 1.1.
76. Kent, IV y Peifer (2002).
77. McCammond y Sulway (2017).
78. McCammond (2017), págs. 14-17.
79. Paolini y Salvetti (2021).
80. McCammond (2017), pág. 17.
81. McCammond (2017), pág. 11.
82. Charney y Peifer (2003), págs. 587–8.
83. Charney y Peifer (2003), pág. 588.
84. Agosto (2002).
85. Charney y Peifer (2003), págs. 586.
86. Björner y Brenti (2005), Capítulo 8.
87. Hanusa y Jones (2012).
88. Björner y Brenti (2005), pág. 24.
89. Björner y Brenti (2005), pág. 293.
90. Green (2002).

Notas

1. Más precisamente, toda relación entre generadores puede explicarse mediante las relaciones dadas, de modo que el grupo es el más grande entre todos los grupos cuyos generadores satisfacen las relaciones dadas. La versión formal de esta definición se da en términos de cocientes de grupos libres .
2. De hecho, lo mismo es cierto para cualquier grupo de Coxeter afín.
3. Las tres posiciones i , j y k no necesitan estar en una sola ventana. Por ejemplo, la permutación afín w en con notación de ventana no es completamente conmutativa, porque , y , aunque ninguna de las cuatro posiciones consecutivas contenga una subsecuencia decreciente de longitud tres. ^[46] ${\displaystyle {\widetilde {S}}_{4}}$ ${\displaystyle [-4,-1,1,14]}$ ${\displaystyle w(0)=10}$ ${\displaystyle w(3)=1}$ ${\displaystyle w(5)=0}$
4. Un tabloide es un relleno del diagrama de Young con entradas distintas, donde dos rellenos son equivalentes si difieren en el orden de los elementos en las filas. Son equinumerosos con los cuadros estrictos por filas, en los que se requiere que las entradas aumenten a lo largo de las filas (mientras que los cuadros de Young estándar tienen entradas que aumentan a lo largo de las filas y hacia abajo en las columnas). ^[53]
5. En otras palabras, uno podría estar interesado en cambiar de una acción grupal de izquierda a una acción de derecha o viceversa. ^[54]
6. En el grupo simétrico finito , la distinción análoga es entre las formas activa y pasiva de una permutación. ^[56] ${\displaystyle S_{n}}$
7. No toda secuencia de n números enteros no negativos es una secuencia de malabarismo. En particular, una secuencia corresponde a un "patrón de malabarismo simple", en el que se atrapa y lanza una pelota a la vez, si y solo si la función es una permutación de . ^[59] ${\displaystyle i\mapsto i+a_{i}\mod {n}}$ ${\displaystyle \{1,\ldots ,n\}}$
8. En algunas fuentes, las reflexiones unitarias se denominan pseudorreflexiones . ^[64]
9. las álgebras de Lie semisimples de dimensión finita , admiten una parametrización explícita de sus módulos integrables de mayor peso ; mientras que no existe una teoría general correspondiente para las álgebras de Lie generales de dimensión infinita. ^[68]

Obras citadas

• Allcock, Daniel (2002), "Imágenes de trenzas para grupos de Artin", Trans. Amer. Math. Soc. , 354 (9): 3455–3474, doi : 10.1090/S0002-9947-02-02944-6 , S2CID  14473723
• Beazley, Elizabeth; Nichols, Margaret; Park, Min Hae; Shi, XiaoLin; Youcis, Alexander (2015), "Proyecciones biyectivas sobre cocientes parabólicos de grupos de Weyl afines", J. Algebr. Comb. , 41 (4): 911–948, arXiv : 1212.0771 , doi : 10.1007/s10801-014-0559-9
• Berg, Chris; Jones, Brant; Vazirani, Monica (2009), "Una biyección en particiones de núcleo y un cociente parabólico del grupo simétrico afín", J. Combin. Theory Ser. A , 116 (8): 1344–1360, arXiv : 0804.1380 , doi :10.1016/j.jcta.2009.03.013, S2CID  3032099
• Billey, Sara C. ; Jockusch, William; Stanley, Richard P. (1993), "Algunas propiedades combinatorias de los polinomios de Schubert", J. Algebr. Comb. , 2 (4): 345–374, doi : 10.1023/A:1022419800503 , hdl : 2027.42/46173 , S2CID  8628113
• Björner, Anders ; Brenti, Francesco (1996), "Permutaciones afines de tipo A", Electron. J. Combinar. , 3 (2): R18, doi : 10.37236/1276 , S2CID  2987208
• Björner, Anders ; Brenti, Francesco (2005), Combinatoria de grupos Coxeter , Springer, doi :10.1007/3-540-27596-7, ISBN 978-3540-442387, Identificador único  115235335
• Cameron, Peter J. (1994), Combinatoria: temas, técnicas, algoritmos , Cambridge University Press, doi : 10.1017/CBO9780511803888, ISBN 978-0-521-45761-3, Número de identificación del sujeto  115451799
• Charney, Ruth ; Peifer, David (2003), "La conjetura de - para los grupos de briadas afines", Comment. Math. Helv. , 78 (3): 584–600, doi : 10.1007/S00014-003-0764-Y , S2CID  54016405 ${\displaystyle K(\pi ,1)}$
• Chmutov, Michael; Lewis, Joel Brewster; Pylyavskyy, Pavlo (2022), "Una generalización afín de la evacuación", Selecta Math. , Nueva serie, 28 (4): Artículo 67, arXiv : 1706.00471 , doi :10.1007/s00029-022-00779-x, S2CID  119168718
• Chmutov, Michael; Frieden, Gabriel; Kim, Dongkwan; Lewis, Joel Brewster; Yudovina, Elena (2022), "Monodromía en células Kazhdan-Lusztig en el tipo afín A", Math. Annalen , 386 (3–4): 1891–1949, arXiv : 1806.07429 , doi :10.1007/s00208-022-02434-4, S2CID  119669284
• Chmutov, Michael; Pylyavskyy, Pavlo; Yudovina, Elena (2018), "Construcción de correspondencia afín Robinson-Schensted con matriz de bolas", Selecta Math. , New Series, 24 (2): 667–750, arXiv : 1511.05861 , doi :10.1007/s00029-018-0402-6, S2CID  119086049
• Clark, Eric; Ehrenborg, Richard (2011), "Excedencias de permutaciones afines", Advances in Applied Mathematics , 46 (1–4): 175–191, doi : 10.1016/j.aam.2009.12.006 , S2CID  15349463
• Coxeter, HSM (1973), Politopos regulares (3.ª ed.), Dover, ISBN 0-486-61480-8
• Crites, Andrew (2010), "Enumeración de la evitación de patrones para permutaciones afines", Electron. J. Combin. , 17 (1): R127, arXiv : 1002.1933 , doi : 10.37236/399 , S2CID  15383510
• Ehrenborg, Richard ; Readdy, Margaret (1996), "Malabarismo y aplicaciones a los análogos q ", Discrete Math. , 157 (1–3): 107–125, CiteSeerX  10.1.1.8.6684 , doi :10.1016/S0012-365X(96)83010-X, S2CID  18149014
• Eriksson, Henrik; Eriksson, Kimmo (1998), "Grupos afines de Weyl como permutaciones infinitas", Electron. J. Combinar. , 5 : R18, doi : 10.37236/1356 , S2CID  218962
• Gallian, Joseph A. (2013), Álgebra abstracta contemporánea (8.ª ed.), Brooks/Cole, ISBN 978-1-133-59970-8, núm. de licencia de conducir  2012938179
• Green, RM (2002), "Sobre la 321-Evitación de permutaciones en grupos de Weyl afines", J. Algebr. Comb. , 15 (3): 241–252, doi : 10.1023/A:1015012524524 , S2CID  10583938
• Hanusa, Christopher RH; Jones, Brant C. (2010), "La enumeración de permutaciones afines completamente conmutativas", Eur. J. Comb. , 31 (5): 1342–1359, arXiv : 0907.0709 , doi :10.1016/j.ejc.2009.11.010, S2CID  789357
• Hanusa, Christopher RH; Jones, Brant C. (2012), "Modelos de ábaco para cocientes parabólicos de grupos de Weyl afines", J. Algebra , 361 : 134–162, arXiv : 1105.5333v2 , doi : 10.1016/j.jalgebra.2012.03.029 , S2CID  47583179
• Humphreys, James E. (1990), Grupos de reflexión y grupos de Coxeter , Cambridge University Press, doi :10.1017/CBO9780511623646, ISBN 0-521-37510-X, Número de identificación del sujeto  121077209
• Kac, Victor G. (1990), Álgebras de Lie de dimensión infinita (PDF) (3.ª ed.), Cambridge University Press, doi :10.1017/CBO9780511626234, ISBN 0-521-46693-8
• Kane, Richard (2001), Grupos de reflexión y teoría invariante , CMS Books in Mathematics/Ouvrages de Mathématiques de la SMC, Springer-Verlag, doi :10.1007/978-1-4757-3542-0, ISBN 0-387-98979-X, Número de identificación del sujeto  119694827
• Kent, IV, Richard P.; Peifer, David (2002), "Una descripción geométrica y algebraica de grupos trenzados anulares", Conferencia internacional sobre métodos geométricos y combinatorios en teoría de grupos y teoría de semigrupos (Lincoln, NE, 2000), Internat. J. Algebra Comput. , 12 (1–2): 85–97, doi :10.1142/S0218196702000997, S2CID  13593688
• Knutson, Allen ; Lam, Thomas; Speyer, David E. (2013), "Variedades de positroides: malabarismo y geometría", Compositio Mathematica , 149 (10): 1710–1752, arXiv : 0903.3694 , doi : 10.1112/S0010437X13007240 , S2CID  16108179
• Lam, Thomas (2015), "La forma de un elemento aleatorio afín del grupo de Weyl y particiones aleatorias del núcleo", Ann. Probab. , 43 (4): 1643–1662, arXiv : 1102.4405v3 , doi : 10.1214/14-AOP915 , S2CID  119691692
• Lapointe, Luc; Morse, Jennifer (2005), "Cuadros sobre núcleos -, palabras reducidas para permutaciones afines y expansiones -Schur", J. Combin. Theory Ser. A , 112 (1): 44–81, doi : 10.1016/j.jcta.2005.01.003 , S2CID  161241 ${\displaystyle k+1}$ ${\displaystyle k}$
• Lehrer, Gustav I.; Taylor, Donald E. (2009), Grupos de reflexión unitaria , Serie de conferencias de la Sociedad Matemática Australiana, vol. 20, Cambridge University Press , ISBN 978-0-521-74989-3, Sr.  2542964
• Lewis, Joel Brewster (2020), "Una nota sobre la acción de Hurwitz en las factorizaciones de reflexión de elementos de Coxeter en grupos de reflexión complejos", Electron. J. Combin. , 27 (2): P2.54, arXiv : 2001.08238 , doi : 10.37236/9351 , S2CID  219176795
• Lewis, Joel Brewster; McCammond, Jon; Petersen, T. Kyle; Schwer, Petra (2019), "Cálculo de la longitud de reflexión en un grupo de Coxeter afín", Trans. Amer. Math. Soc. , 371 (6): 4097–4127, arXiv : 1710.06920 , doi :10.1090/tran/7472, S2CID  119617021
• Lewis, Joel Brewster; Reiner, Victor (2016), "Circuitos y acción de Hurwitz en sistemas de raíces finitas", The New York Journal of Mathematics , 22 : 1457–1486, arXiv : 1603.05969 , MR  3603073, S2CID  1789116
• Lusztig, George (1983), "Algunos ejemplos de representaciones integrables cuadradas de grupos p -ádicos semisimples", Trans. Amer. Math. Soc. , 277 : 623–653, doi : 10.1090/S0002-9947-1983-0694380-4 , S2CID  54190838
• McCammond, Jon (2017), "La misteriosa geometría de los grupos de Artin", Winter Braids Lect. Notes , 4 (Winter Braids VII (Caen, 2017)): Exp. No. 1, 30, doi : 10.5802/wbln.17 , S2CID  128279613
• McCammond, Jon; Sulway, Robert (2017), "Grupos de Artin de tipo euclidiano", Invent. Math. , 210 (1): 231–282, arXiv : 1312.7770 , Bibcode :2017InMat.210..231M, doi :10.1007/s00222-017-0728-2, S2CID  253738806
• Paolini, Giovanni; Salvetti, Mario (2021), "Prueba de la conjetura para grupos afines de Artin", Inventar. Matemáticas. , 224 (2): 487–572, arXiv : 1907.11795 , doi : 10.1007/s00222-020-01016-y, S2CID  253738279 ${\displaystyle K(\pi ,1)}$
• Petersen, T. Kyle (2015), Números eulerianos , Textos avanzados de Birkhäuser Basler Lehrbücher, Birkhauser, doi :10.1007/978-1-4939-3091-3, ISBN 978-1-4939-3090-6
• Polster, Burkard (2003), Las matemáticas del malabarismo , Springer, doi :10.1007/b98883, ISBN 0-387-95513-5, Número de identificación del sujeto  221274895
• Reiner, Victor (1995), "La distribución de descendencias y longitud en un grupo de Coxeter", Electron. J. Combin. , 2 : R25, doi : 10.37236/1219 , S2CID  6602595
• Shephard, GC ; Todd, JA (1954), "Grupos de reflexión unitaria finitos", Canad. J. Math. , 6 : 274–304, doi : 10.4153/CJM-1954-028-3 , S2CID  3342221
• Shi, Jian-Yi (1986), Las células de Kazhdan-Lusztig en ciertos grupos de Weyl afines , Lecture Notes in Mathematics, vol. 1179, Springer, doi :10.1007/bfb0074968, ISBN 3-540-16439-1, Número de identificación del sujeto  117899042
• Shi, Jian Yi (1987), "Nichos correspondientes a un grupo de Weyl afín", J. London Math. Soc. , 2, 35 (1): 42–55, doi :10.1112/jlms/s2-35.1.42, S2CID  119897519
• Shi, Jian-Yi (1991), "El algoritmo generalizado de Robinson–Schensted en el grupo de Weyl afín de tipo A _{n −1} ", J. Algebra , 139 (2): 364–394, CiteSeerX  10.1.1.551.3094 , doi :10.1016/0021-8693(91)90300-W, S2CID  124324517
• Shi, Jian-Yi (2002), "Ciertos grupos de reflexión imprimitiva y sus versiones genéricas", Trans. Amer. Math. Soc. , 354 (5): 2115–2129, doi : 10.1090/S0002-9947-02-02941-0 , S2CID  53996908
• Stembridge, John (1996), "Sobre los elementos completamente conmutativos de los grupos de Coxeter", J. Algebr. Comb. , 5 (4): 353–385, doi : 10.1007/BF00193185 , hdl : 2027.42/46260 , S2CID  195239538
• Viennot, G. (1977), "Une forme géométrique de la correspondencia de Robinson-Schensted", en Foata, Dominique (ed.), Combinatoire et Représentation du Groupe Symétrique , Lecture Notes in Mathematics (en francés), vol. 579, Springer, págs. 29–58, doi :10.1007/BFb0090011, ISBN 978-3-540-08143-2, Número de identificación del sujeto  118727388