Modelización matemática de enfermedades infecciosas.

Uso de modelos matemáticos para comprender la transmisión de enfermedades infecciosas

Los modelos matemáticos pueden proyectar cómo progresan las enfermedades infecciosas para mostrar el resultado probable de una epidemia (incluso en las plantas ) y ayudar a informar las intervenciones de salud pública y sanidad vegetal. Los modelos utilizan suposiciones básicas o estadísticas recopiladas junto con matemáticas para encontrar parámetros para diversas enfermedades infecciosas y utilizan esos parámetros para calcular los efectos de diferentes intervenciones, como programas de vacunación masiva. El modelado puede ayudar a decidir qué intervención(es) evitar y cuál probar, o puede predecir patrones de crecimiento futuros, etc.

Historia

La modelización de enfermedades infecciosas es una herramienta que se ha utilizado para estudiar los mecanismos por los que se propagan las enfermedades, predecir el curso futuro de un brote y evaluar estrategias para controlar una epidemia. ^[1]

El primer científico que intentó cuantificar sistemáticamente las causas de muerte fue John Graunt en su libro Natural and Political Observations made upon the Bills of Mortality , en 1662. Los proyectos de ley que estudió eran listados de números y causas de muerte publicados semanalmente. El análisis de Graunt sobre las causas de muerte se considera el comienzo de la "teoría de los riesgos competitivos" que, según Daley y Gani ^[1], es "una teoría que ahora está bien establecida entre los epidemiólogos modernos".

El primer relato de modelización matemática de la propagación de enfermedades fue realizado en 1760 por Daniel Bernoulli . Formado como médico, Bernoulli creó un modelo matemático para defender la práctica de la inoculación contra la viruela . ^[2] Los cálculos de este modelo mostraron que la inoculación universal contra la viruela aumentaría la esperanza de vida de 26 años 7 meses a 29 años 9 meses. ^[3] El trabajo de Daniel Bernoulli precedió a la comprensión moderna de la teoría de los gérmenes . ^[4]

A principios del siglo XX, William Hamer ^[5] y Ronald Ross ^[6] aplicaron la ley de acción de masas para explicar el comportamiento epidémico.

En la década de 1920 surgieron los modelos compartimentales. El modelo epidémico de Kermack-McKendrick (1927) y el modelo epidémico de Reed-Frost (1928) describen la relación entre individuos susceptibles , infectados e inmunes en una población. El modelo epidémico de Kermack-McKendrick logró predecir el comportamiento de los brotes de manera muy similar al observado en muchas epidemias registradas. ^[7]

Recientemente, se han utilizado modelos basados ​​en agentes (ABM) en lugar de modelos compartimentales más simples . ^[8] Por ejemplo, los ABM epidemiológicos se han utilizado para informar intervenciones de salud pública (no farmacéuticas) contra la propagación del SARS-CoV-2 . ^[9] Los ABM epidemiológicos, a pesar de su complejidad y de requerir un alto poder computacional, han sido criticados por supuestos simplificadores y poco realistas. ^{[10] [11]} Aún así, pueden ser útiles para informar decisiones sobre medidas de mitigación y supresión en los casos en que los ABM están calibrados con precisión. ^[12]

Suposiciones

Los modelos son tan buenos como los supuestos en los que se basan. Si un modelo hace predicciones que no están en línea con los resultados observados y las matemáticas son correctas, los supuestos iniciales deben cambiar para que el modelo sea útil. ^[13]

• Distribución de edades rectangular y estacionaria , es decir, todos los miembros de la población viven hasta la edad L y luego mueren, y para cada edad (hasta L ) hay el mismo número de personas en la población. Esto suele estar bien justificado en los países desarrollados donde la mortalidad infantil es baja y gran parte de la población vive según la esperanza de vida.
• Mezcla homogénea de la población, es decir, los individuos de la población bajo escrutinio se agrupan y hacen contacto al azar y no se mezclan principalmente en un subgrupo más pequeño. Esta suposición rara vez se justifica porque la estructura social está muy extendida. Por ejemplo, la mayoría de la gente en Londres sólo establece contacto con otros londinenses. Además, dentro de Londres hay subgrupos más pequeños, como la comunidad turca o los adolescentes (solo por dar dos ejemplos), que se mezclan entre sí más que personas fuera de su grupo. Sin embargo, la mezcla homogénea es una suposición estándar para que las matemáticas sean manejables.

Tipos de modelos epidémicos

estocástico

"Estocástico" significa ser o tener una variable aleatoria. Un modelo estocástico es una herramienta para estimar distribuciones de probabilidad de resultados potenciales al permitir variaciones aleatorias en una o más entradas a lo largo del tiempo. Los modelos estocásticos dependen de las variaciones aleatorias en el riesgo de exposición, enfermedad y otras dinámicas de enfermedad. La diseminación estadística de la enfermedad a nivel de agente en poblaciones pequeñas o grandes se puede determinar mediante métodos estocásticos. ^{[14] [15] [16]}

determinista

Cuando se trata de poblaciones grandes, como en el caso de la tuberculosis, se suelen utilizar modelos matemáticos deterministas o compartimentales. En un modelo determinista, los individuos de la población se asignan a diferentes subgrupos o compartimentos, cada uno de los cuales representa una etapa específica de la epidemia. ^[17]

Las tasas de transición de una clase a otra se expresan matemáticamente como derivadas, por lo que el modelo se formula mediante ecuaciones diferenciales. Al construir tales modelos, se debe suponer que el tamaño de la población en un compartimento es diferenciable con respecto al tiempo y que el proceso epidémico es determinista. En otras palabras, los cambios en la población de un compartimento se pueden calcular utilizando únicamente la historia que se utilizó para desarrollar el modelo. ^[7]

Crecimiento subexponencial

Una explicación común para el crecimiento de las epidemias sostiene que 1 persona infecta a 2, esas 2 infectan a 4 y así sucesivamente, duplicándose el número de infectados en cada generación. Es análogo a un juego de etiqueta donde 1 persona etiqueta a 2, esas 2 etiquetan a otras 4 que nunca han sido etiquetadas y así sucesivamente. A medida que este juego avanza, se vuelve cada vez más frenético a medida que los etiquetados pasan corriendo junto a los previamente etiquetados para cazar a aquellos que nunca han sido etiquetados. Así, este modelo de epidemia conduce a una curva que crece exponencialmente hasta llegar a cero, ya que toda la población ha sido infectada. es decir, no hay inmunidad colectiva ni un pico y un declive gradual como se ve en la realidad. ^[18]

Modelos epidémicos en redes

Las epidemias pueden modelarse como enfermedades que se propagan a través de redes de contacto entre personas. Una red de este tipo se puede representar matemáticamente mediante un gráfico y se denomina red de contactos. ^[19] Cada nodo en una red de contactos es una representación de un individuo y cada enlace (borde) entre un par de nodos representa el contacto entre ellos. Los vínculos en las redes de contactos pueden usarse para transmitir la enfermedad entre los individuos y cada enfermedad tiene su propia dinámica además de su red de contactos. La combinación de dinámicas de enfermedades bajo la influencia de intervenciones, si las hubiera, en una red de contactos puede modelarse con otra red, conocida como red de transmisión. En una red de transmisión, todos los eslabones son responsables de transmitir la enfermedad. Si dicha red es una red local similar a un árbol, lo que significa que cualquier vecindad local en dicha red toma la forma de un árbol , entonces la reproducción básica se puede escribir en términos del grado excesivo promedio de la red de transmisión de manera que:

$${\displaystyle R_{0}={\frac {\langle k^{2}\rangle }{\langle k\rangle }}-1,}$$

donde es el grado medio (grado promedio) de la red y es el segundo momento de la distribución de grados de la red de transmisión . Sin embargo, no siempre es sencillo encontrar la red de transmisión a partir de la red de contactos y la dinámica de la enfermedad. ^[20] Por ejemplo, si una red de contactos se puede aproximar con un gráfico Erdős-Rényi con una distribución de grados Poissonianos , y los parámetros de propagación de enfermedades son como se definen en el ejemplo anterior, es decir, la tasa de transmisión por persona y la enfermedad ha un período infeccioso medio de , entonces el número de reproducción básico es ^{[21] [22]} ya que para una distribución de Poisson. ${\displaystyle {\langle k\rangle }}$ ${\displaystyle {\langle k^{2}\rangle }}$ ${\displaystyle \beta }$ ${\displaystyle {\dfrac {1}{\gamma }}}$ ${\displaystyle R_{0}={\dfrac {\beta }{\gamma }}{\langle k\rangle }}$ ${\displaystyle {\langle k^{2}\rangle }-{\langle k\rangle }^{2}={\langle k\rangle }}$

Número de reproducción

El número de reproducción básico (indicado por R ₀ ) es una medida de cuán transferible es una enfermedad. Es el número promedio de personas que una sola persona infecciosa infectará durante el transcurso de su infección. Esta cantidad determina si la infección aumentará subexponencialmente , desaparecerá o permanecerá constante: si R ₀ > 1, entonces cada persona infecta en promedio a más de una persona, por lo que la enfermedad se propagará; si R ₀ < 1, entonces cada persona infecta a menos de una en promedio, por lo que la enfermedad desaparecerá; y si R ₀ = 1, entonces cada persona infectará en promedio exactamente a otra persona, por lo que la enfermedad se volverá endémica: se moverá por toda la población pero no aumentará ni disminuirá. ^[23]

Estado estacionario endémico

Se dice que una enfermedad infecciosa es endémica cuando puede mantenerse en una población sin necesidad de insumos externos. Esto significa que, en promedio, cada persona infectada está infectando exactamente a otra persona (más y el número de personas infectadas crecerá subexponencialmente y habrá una epidemia ; menos y la enfermedad desaparecerá). En términos matemáticos, eso es:

${\displaystyle \ R_{0}S\ =1.}$

El número de reproducción básico ( R ₀ ) de la enfermedad, suponiendo que todos sean susceptibles, multiplicado por la proporción de la población que es realmente susceptible ( S ) debe ser uno (ya que aquellos que no son susceptibles no figuran en nuestros cálculos porque no pueden contraer la enfermedad). Obsérvese que esta relación significa que para que una enfermedad se encuentre en el estado estacionario endémico , cuanto mayor sea el número de reproducción básico, menor debe ser la proporción de la población susceptible, y viceversa. Esta expresión tiene limitaciones en cuanto a la proporción de susceptibilidad, por ejemplo, R ₀ es igual a 0,5 implica que S tiene que ser 2, sin embargo, esta proporción excede el tamaño de la población. ^{[ cita necesaria ]}

Supongamos la distribución de edades estacionaria rectangular y consideremos también que las edades de infección tienen la misma distribución para cada año de nacimiento. Sea A la edad promedio de infección , por ejemplo cuando los individuos más jóvenes que A son susceptibles y los mayores que A son inmunes (o infecciosos). Entonces se puede demostrar mediante un argumento sencillo que la proporción de la población que es susceptible viene dada por:

${\displaystyle S={\frac {A}{L}}.}$

Reiteramos que L es la edad a la que en este modelo se supone que muere cada individuo. Pero la definición matemática del estado estacionario endémico se puede reordenar para dar:

${\displaystyle S={\frac {1}{R_{0}}}.}$

Por tanto, debido a la propiedad transitiva :

${\displaystyle {\frac {1}{R_{0}}}={\frac {A}{L}}\Rightarrow R_{0}={\frac {L}{A}}.}$

Esto proporciona una forma sencilla de estimar el parámetro R ₀ utilizando datos fácilmente disponibles.

Para una población con una distribución de edades exponencial ,

${\displaystyle R_{0}=1+{\frac {L}{A}}.}$

Esto permite calcular el número de reproducción básico de una enfermedad dados A y L en cualquier tipo de distribución poblacional.

Modelos compartimentales en epidemiología.

Los modelos compartimentales se formulan como cadenas de Markov . ^[24] Un modelo compartimental clásico en epidemiología es el modelo SIR, que puede usarse como un modelo simple para modelar epidemias. También se emplean muchos otros tipos de modelos compartimentales.

El modelo SIR

Diagrama del modelo SIR con valores iniciales y tasas de infección y recuperación. ${\textstyle S(0)=997,I(0)=3,R(0)=0}$ ${\textstyle \beta =0.4}$ ${\textstyle \gamma =0.04}$

Animación del modelo SIR con valores iniciales y tasa de recuperación . La animación muestra el efecto de reducir la tasa de infección de a . Si no hay medicamentos o vacunas disponibles, sólo es posible reducir la tasa de infección (lo que a menudo se denomina " aplanar la curva ") mediante medidas adecuadas, como el distanciamiento social. ${\textstyle S(0)=997,I(0)=3,R(0)=0}$ ${\textstyle \gamma =0.04}$ ${\textstyle \beta =0.5}$ ${\textstyle \beta =0.12}$

En 1927, WO Kermack y AG McKendrick crearon un modelo en el que consideraban una población fija con sólo tres compartimentos: susceptible, ; infectado, ; y recuperado, . Los compartimentos utilizados para este modelo constan de tres clases: ^[25] ${\displaystyle S(t)}$ ${\displaystyle I(t)}$ ${\displaystyle R(t)}$

• ${\displaystyle S(t)}$se utiliza para representar a los individuos que aún no están infectados con la enfermedad en el momento t, o aquellos susceptibles a la enfermedad de la población.
• ${\displaystyle I(t)}$denota los individuos de la población que han sido infectados con la enfermedad y son capaces de transmitirla a aquellos en la categoría susceptible.
• ${\displaystyle R(t)}$es el compartimento utilizado para los individuos de la población que han sido infectados y luego eliminados de la enfermedad, ya sea por inmunización o por fallecimiento. Aquellos en esta categoría no pueden volver a infectarse ni transmitir la infección a otros.

Otros modelos compartimentados

Hay muchas modificaciones del modelo SIR, incluidas aquellas que incluyen nacimientos y muertes, donde al recuperarse no hay inmunidad (modelo SIS), donde la inmunidad dura solo un corto período de tiempo (SIRS), donde hay un período latente de la enfermedad donde la persona no es infecciosa ( SEIS y SEIR ), y donde los bebés pueden nacer con inmunidad (MSIR). ^{[ cita necesaria ]}

Dinámica de las enfermedades infecciosas

Los modelos matemáticos deben integrar el creciente volumen de datos que se generan sobre las interacciones entre el huésped y el patógeno . Muchos estudios teóricos sobre la dinámica demográfica , la estructura y la evolución de las enfermedades infecciosas de plantas y animales, incluido el hombre, se ocupan de este problema. ^[26]

Los temas de investigación incluyen:

• cambio antigénico
• redes epidemiológicas
• evolución y propagación de la resistencia
• inmunoepidemiología​
• dinámica intra-host
• Pandemia
• genética de poblaciones de patógenos
• persistencia de patógenos dentro del huésped
• filodinámica
• Papel e identificación de reservorios de infección.
• papel de los factores genéticos del huésped
• epidemiología espacial
• herramientas e innovaciones estadísticas y matemáticas
• Estructura e interacciones de las cepas (biología)
• transmisión , propagación y control de la infección
• virulencia

Matemáticas de la vacunación masiva

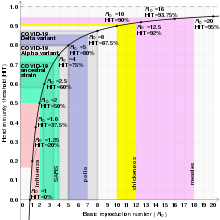
Si la proporción de la población que es inmune excede el nivel de inmunidad colectiva para la enfermedad, entonces la enfermedad ya no puede persistir en la población y su transmisión desaparece. ^[27] Por lo tanto, una enfermedad puede eliminarse de una población si suficientes individuos son inmunes debido a la vacunación o a la recuperación de una exposición previa a la enfermedad. Por ejemplo, la erradicación de la viruela , con el último caso salvaje en 1977, y la certificación de la erradicación de la transmisión autóctona de 2 de los 3 tipos de poliovirus salvaje (el tipo 2 en 2015, tras el último caso notificado en 1999, y el tipo 3 en 2019). , después del último caso reportado en 2012). ^[28]

El nivel de inmunidad colectiva se denominará q . Recuerde que, para un estado estable: ^{[ cita necesaria ]}

${\displaystyle R_{0}\cdot S=1.}$

Sucesivamente,

${\displaystyle R_{0}={\frac {N}{S}}={\frac {\mu N\operatorname {E} (T_{L})}{\mu N\operatorname {E} [\min(T_{L},T_{S})]}}={\frac {\operatorname {E} (T_{L})}{\operatorname {E} [\min(T_{L},T_{S})]}},}$

que es aproximadamente: ^{[ cita necesaria ]}

${\displaystyle {\frac {\operatorname {\operatorname {E} } (T_{L})}{\operatorname {\operatorname {E} } (T_{S})}}=1+{\frac {\lambda }{\mu }}={\frac {\beta N}{v}}.}$

Gráfico del umbral de inmunidad colectiva frente al número de reproducción básico con enfermedades seleccionadas

S será (1 −  q ), ya que q es la proporción de la población que es inmune y q  +  S debe ser igual a uno (ya que en este modelo simplificado, todos son susceptibles o inmunes). Entonces:

${\displaystyle {\begin{aligned}&R_{0}\cdot (1-q)=1,\\[6pt]&1-q={\frac {1}{R_{0}}},\\[6pt]&q=1-{\frac {1}{R_{0}}}.\end{aligned}}}$

Recuerde que este es el nivel umbral. La desaparición de la transmisión sólo se producirá si la proporción de individuos inmunes supera este nivel debido a un programa de vacunación masiva.

Acabamos de calcular el umbral crítico de inmunización ₍ denotado qc ). Es la proporción mínima de la población que debe ser inmunizada al nacer (o cerca del nacimiento) para que la infección desaparezca en la población.

${\displaystyle q_{c}=1-{\frac {1}{R_{0}}}.}$

Porque la fracción del tamaño final de la población p que nunca se infecta se puede definir como:

${\displaystyle \lim _{t\to \infty }S(t)=e^{-\int _{0}^{\infty }\lambda (t)\,dt}=1-p.}$

Por eso,

${\displaystyle p=1-e^{-\int _{0}^{\infty }\beta I(t)\,dt}=1-e^{-R_{0}p}.}$

Resolviendo para , obtenemos: ${\displaystyle R_{0}}$

${\displaystyle R_{0}={\frac {-\ln(1-p)}{p}}.}$

Cuando la vacunación masiva no puede superar la inmunidad colectiva

Si la vacuna utilizada no es suficientemente eficaz o no se puede alcanzar la cobertura requerida, es posible que el programa no supere q _c . Un programa de este tipo protegerá a las personas vacunadas de las enfermedades, pero puede cambiar la dinámica de transmisión. ^{[ cita necesaria ]}

Supongamos que una proporción de la población q (donde q < q _c ) está inmunizada al nacer contra una infección con R ₀  > 1. El programa de vacunación cambia R ₀ a R _q donde

${\displaystyle R_{q}=R_{0}(1-q)}$

Este cambio se produce simplemente porque ahora hay menos personas susceptibles en la población que pueden infectarse. R _q es simplemente R ₀ menos aquellos que normalmente estarían infectados pero que no pueden estarlo ahora ya que son inmunes.

Como consecuencia de este número de reproducción básico más bajo , la edad promedio de infección A también cambiará a algún nuevo valor A _q en aquellos que no han sido vacunados.

Recuerde la relación que unía R ₀ , A y L . Suponiendo que la esperanza de vida no haya cambiado, ahora: ^{[ cita necesaria ]}

${\displaystyle R_{q}={\frac {L}{A_{q}}},}$

${\displaystyle A_{q}={\frac {L}{R_{q}}}={\frac {L}{R_{0}(1-q)}}.}$

Pero R ₀ = L / A entonces:

${\displaystyle A_{q}={\frac {L}{(L/A)(1-q)}}={\frac {AL}{L(1-q)}}={\frac {A}{1-q}}.}$

Por lo tanto, el programa de vacunación puede aumentar la edad promedio de infección y las personas no vacunadas experimentarán una fuerza de infección reducida debido a la presencia del grupo vacunado. En el caso de una enfermedad que provoca una mayor gravedad clínica en las poblaciones de mayor edad, la proporción de la población no vacunada puede experimentar la enfermedad relativamente más tarde en la vida de lo que ocurriría sin la vacuna.

Cuando la vacunación masiva supera la inmunidad colectiva

Si un programa de vacunación hace que la proporción de individuos inmunes en una población supere el umbral crítico durante un período de tiempo significativo, se detendrá la transmisión de la enfermedad infecciosa en esa población. Si la eliminación se produce en todas partes al mismo tiempo, esto puede conducir a la erradicación . ^{[ cita necesaria ]}

Eliminación

La interrupción de la transmisión endémica de una enfermedad infecciosa, que se produce si cada individuo infectado infecta a menos que otro, se logra manteniendo la cobertura de vacunación para mantener la proporción de individuos inmunes por encima del umbral crítico de inmunización. ^{[ cita necesaria ]}

Erradicación

Eliminación en todas partes al mismo tiempo, de modo que el agente infeccioso desaparezca (por ejemplo, viruela y peste bovina ). ^{[ cita necesaria ]}

Fiabilidad

Los modelos tienen la ventaja de examinar múltiples resultados simultáneamente, en lugar de hacer un único pronóstico. Los modelos han mostrado amplios grados de confiabilidad en pandemias pasadas, como el SARS , el SARS-CoV-2 , ^[29] la gripe porcina , el MERS y el Ébola . ^[30]

Ver también

• Número de reproducción básico
• Modelos compartimentales en epidemiología.
• Seguimiento de contactos
• Tamaño crítico de la comunidad
• Vigilancia de enfermedades
• modelo de ecosistema
• Fuerza de infección
• Epidemiología del paisaje
• Matriz de próxima generación
• Pandemia
• Factor de riesgo
• Red sexual
• Matriz WAIFW

Referencias

1. Daley DJ, Gani J (2005). Modelado de epidemias: una introducción . Nueva York: Cambridge University Press.
2. Hethcote HW (2000). "Las matemáticas de las enfermedades infecciosas". Revisión SIAM . 42 (4): 599–653. Código Bib : 2000SIAMR..42..599H. doi :10.1137/S0036144500371907. S2CID  10836889.
3. Soplador S, Bernoulli D (2004). "Un intento de un nuevo análisis de la mortalidad provocada por la viruela y de las ventajas de la inoculación para prevenirla". Reseñas en Virología Médica . 14 (5): 275–88. doi :10.1002/rmv.443. PMID  15334536. S2CID  8169180.
4. "Teoría de los gérmenes: descripción general | Temas de ScienceDirect".
5. Hamer W (1928). Epidemiología antigua y nueva . Londres: Kegan Paul.
6. Ross R (1910). La prevención de la malaria. Dutton.
7. Brauer F, Castillo-Chávez C (2001). Modelos matemáticos en biología y epidemiología de poblaciones . Nueva York: Springer.
8. Eisinger D, Thulke HH (abril de 2008). "La formación de patrones espaciales facilita la erradicación de enfermedades infecciosas". La Revista de Ecología Aplicada . 45 (2): 415–423. Código Bib : 2008JApEc..45..415E. doi :10.1111/j.1365-2664.2007.01439.x. PMC 2326892 . PMID  18784795. 
9. Adam D (abril de 2020). "Informe especial: Las simulaciones que impulsan la respuesta mundial al COVID-19". Naturaleza . 580 (7803): 316–318. Código Bib :2020Natur.580..316A. doi : 10.1038/d41586-020-01003-6 . PMID  32242115. S2CID  214771531.
10. Squazzoni F, Polhill JG, Edmonds B, Ahrweiler P, Antosz P, Scholz G, et al. (2020). "Modelos computacionales que importan durante un brote de pandemia global: un llamado a la acción". Revista de Sociedades Artificiales y Simulación Social . 23 (2): 10. doi : 10.18564/jasss.4298 . hdl : 10037/19057 . ISSN  1460-7425. S2CID  216426533.
11. Sridhar D, Majumder MS (abril de 2020). "Modelando la pandemia". BMJ . 369 : m1567. doi : 10.1136/bmj.m1567 . PMID  32317328. S2CID  216074714.
12. Maziarz M, Zach M (octubre de 2020). "Modelado basado en agentes para la predicción de la epidemia de SARS-CoV-2 y la evaluación de la intervención: una evaluación metodológica". Revista de Evaluación en la Práctica Clínica . 26 (5): 1352-1360. doi :10.1111/jep.13459. PMC 7461315 . PMID  32820573. 
13. Huppert, A.; Katriel, G. (2013). "Modelado matemático y predicción en epidemiología de enfermedades infecciosas". Microbiología clínica e infección . 19 (11): 999–1005. doi : 10.1111/1469-0691.12308 . PMID  24266045.
14. Tembine, H. "COVID-19: perspectiva de juego de tipo campo medio basada en datos. Juegos". Diario de juegos. doi : 10.3390/g11040051 . hdl : 10419/257469 . {{cite journal}}: Citar diario requiere |journal=( ayuda )
15. Nakamura, Gilberto M.; Monteiro, Ana Carolina P.; Cardoso, George C.; Martínez, Alexandre S. (febrero de 2017). "Método eficiente para el cálculo integral de la diseminación epidémica a nivel de agente en redes". Informes científicos . 7 (1): 40885. arXiv : 1606.07825 . Código Bib : 2017NatSR...740885N. doi :10.1038/srep40885. ISSN  2045-2322. PMC 5247741 . PMID  28106086. 
16. Nakamura, Gilberto M.; Cardoso, George C.; Martínez, Alexandre S. (febrero de 2020). "Ecuaciones epidémicas susceptibles-infecciosas-susceptibles mejoradas basadas en incertidumbres y funciones de autocorrelación". Ciencia abierta de la Royal Society . 7 (2): 191504. Código bibliográfico : 2020RSOS....791504N. doi :10.1098/rsos.191504. ISSN  2054-5703. PMC 7062106 . PMID  32257317. 
17. Dietz, Klaus (1967). "Epidemias y rumores: una encuesta". Revista de la Real Sociedad de Estadística. Serie A (General) . 130 (4): 505–528. doi :10.2307/2982521. JSTOR  2982521.
18. Maier, BF; Brockmann, D. (2020). "La contención eficaz explica el crecimiento subexponencial de los casos recientes confirmados de COVID-19 en China". Ciencia . 368 (6492): 742–746. Código Bib : 2020 Ciencia... 368.. 742 M. doi : 10.1126/ciencia.abb4557. PMC 7164388 . PMID  32269067. 
19. Ciencia en redes de Albert-László Barabási.
20. Quená, Eben; Robins, James M. (septiembre de 2007). "Segunda mirada a la propagación de epidemias en las redes". Revisión física E. 76 (3 parte 2): 036113. arXiv : q-bio/0610057 . Código bibliográfico : 2007PhRvE..76c6113K. doi : 10.1103/PhysRevE.76.036113. ISSN  1539-3755. PMC 2215389 . PMID  17930312. 
21. Pastor-Satorras, Romualdo; Castellano, Claudio; Van Mieghem, Piet; Vespignani, Alessandro (31 de agosto de 2015). "Procesos epidémicos en redes complejas". Reseñas de Física Moderna . 87 (3): 925–979. arXiv : 1408.2701 . Código Bib : 2015RvMP...87..925P. doi : 10.1103/RevModPhys.87.925 . S2CID  14306926.
22. K. Rizi, Abbas; Faqeeh, Ali; Badie-Modiri, Arash; Kivelä, Mikko (20 de abril de 2022). "Propagación de epidemias y rastreo de contactos digitales: efectos de la mezcla heterogénea y fallas de cuarentena". Revisión física E. 105 (4): 044313. arXiv : 2103.12634 . Código bibliográfico : 2022PhRvE.105d4313R. doi : 10.1103/PhysRevE.105.044313 . PMID  35590624. S2CID  232320251.
23. "Número de reproducción básico: descripción general | Temas de ScienceDirect".
24. Cosma Shalizi (15 de noviembre de 2018). "Datos sobre el espacio y el tiempo; Conferencia 21: Modelos compartimentales" (PDF) . Universidad de Carnegie mellon . Consultado el 19 de septiembre de 2020 .
25. Kermack WO, McKendrick AG (1991). "Contribuciones a la teoría matemática de las epidemias - I. 1927". Boletín de Biología Matemática . 53 (1–2): 33–55. Código Bib : 1927RSPSA.115..700K. doi : 10.1007/BF02464423 . JSTOR  94815. PMID  2059741.
26. Brauer, Fred (2017). "Epidemiología matemática: pasado, presente y futuro". Modelado de enfermedades infecciosas . 2 (2): 113–127. doi :10.1016/j.idm.2017.02.001. PMC 6001967 . PMID  29928732. 
27. Britton, Tom; Bola, Frank; Trampa, Pieter (2020). "Un modelo matemático revela la influencia de la heterogeneidad de la población en la inmunidad colectiva al SARS-CoV-2". Ciencia . 369 (6505): 846–849. Código Bib : 2020 Ciencia... 369..846B. doi : 10.1126/ciencia.abc6810. PMC 7331793 . PMID  32576668. 
28. Pollard, Andrew J.; Bijker, Else M. (2021). "Una guía de vacunología: desde los principios básicos hasta los nuevos desarrollos". Inmunología de Reseñas de la Naturaleza . 21 (2): 83-100. doi :10.1038/s41577-020-00479-7. PMC 7754704 . PMID  33353987. 
29. Renz, Alina; Widerspick, Lina; Dräger, Andreas (2020). "FBA revela la guanilato quinasa como un objetivo potencial para terapias antivirales contra el SARS-CoV-2". Bioinformática . 36 (Suplemento_2): i813–i821. doi : 10.1093/bioinformática/btaa813. PMC 7773487 . PMID  33381848. 
30. Costris-Vas C, Schwartz EJ, Smith? RJ (noviembre de 2020). "Predecir el COVID-19 utilizando pandemias pasadas como guía: ¿qué tan confiables eran los modelos matemáticos entonces y qué tan confiables serán ahora?". Biociencias Matemáticas e Ingeniería . 17 (6): 7502–7518. doi : 10.3934/mbe . PMID  33378907.

Otras lecturas

• Keeling M, Rohani P. Modelado de enfermedades infecciosas: en humanos y animales . Princeton: Prensa de la Universidad de Princeton.
• von Csefalvay C. Modelado computacional de enfermedades infecciosas. Cambridge, MA: Elsevier/Academic Press . Consultado el 27 de febrero de 2023 .
• Vynnycky E, Blanco RG. Introducción al modelado de enfermedades infecciosas . Consultado el 15 de febrero de 2016 .Un libro introductorio sobre modelos de enfermedades infecciosas y sus aplicaciones.
• Grassly NC, Fraser C (junio de 2008). "Modelos matemáticos de transmisión de enfermedades infecciosas". Reseñas de la naturaleza. Microbiología . 6 (6): 477–87. doi :10.1038/nrmicro1845. PMC  7097581 . PMID  18533288.
• Boily MC, Mâsse B (julio-agosto de 1997). "Modelos matemáticos de transmisión de enfermedades: una valiosa herramienta para el estudio de las enfermedades de transmisión sexual". Revista Canadiense de Salud Pública . 88 (4): 255–65. doi :10.1007/BF03404793. PMC  6990198 . PMID  9336095.
• Capasso V. Estructuras matemáticas de sistemas epidémicos. Segunda Impresión . Heidelberg, 2008: Springer.{{cite book}}: Mantenimiento CS1: ubicación ( enlace )

enlaces externos

Software

• Model-Builder: software interactivo (basado en GUI) para construir, simular y analizar modelos ODE.
• Simulador GLEaMviz: permite la simulación de enfermedades infecciosas emergentes que se propagan por todo el mundo.
• STEM: Marco de código abierto para modelado epidemiológico disponible a través de la Fundación Eclipse.
• Vigilancia del paquete R : modelado y seguimiento temporal y espacio-temporal de fenómenos epidémicos